Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него – Пифагор
В этой статье:
Матрица смежности
Матрица инцидентности
Список смежности (инцидентности)
Взвешенный граф (коротко)
Итак, мы умеем задавать граф графическим способом. Но есть еще два способа как можно задавать граф, а точнее представлять его. Для экономии памяти в компьютере граф можно представлять с помощью матриц или с помощью списков.
Матрица является удобной для представления плотных графов, в которых число ребер близко к максимально возможному числу ребер (у полного графа).
Другой способ называется списком. Данный способ больше подходит для более разреженных графов, в котором число ребер намного меньше максимально возможного числа ребер (у полного графа).
Перед чтением материала рекомендуется ознакомится с предыдущей статьей, о смежности и инцидентности, где данные определения подробно разбираются.
Матрица смежности
Но тем кто знает, но чуть забыл, что такое смежность есть краткое определение.
Смежность – понятие, используемое только в отношении двух ребер или в отношении двух вершин: два ребра инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.
Матрица (назовем ее L) состоит из n строк и n столбцов и поэтому занимает n^2 места.
Каждая ячейка матрицы равна либо 1, либо 0;
Ячейка в позиции L (i, j) равна 1 тогда и только тогда, когда существует ребро (E) между вершинами (V) i и j. Если у нас положение (j, i), то мы также сможем использовать данное правило. Из этого следует, что число единиц в матрице равно удвоенному числу ребер в графе. (если граф неориентированный). Если ребра между вершинами i и j не существует, то ставится 0.
Для практического примера возьмем самый обыкновенный неориентированный граф:
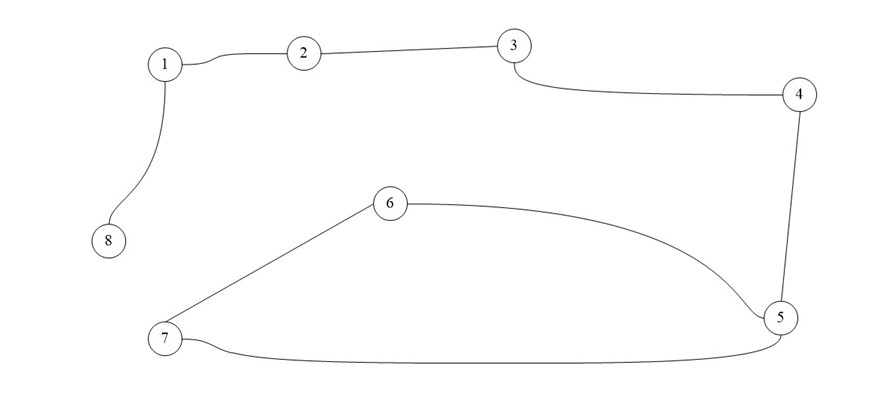
А теперь представим его в виде матрицы:
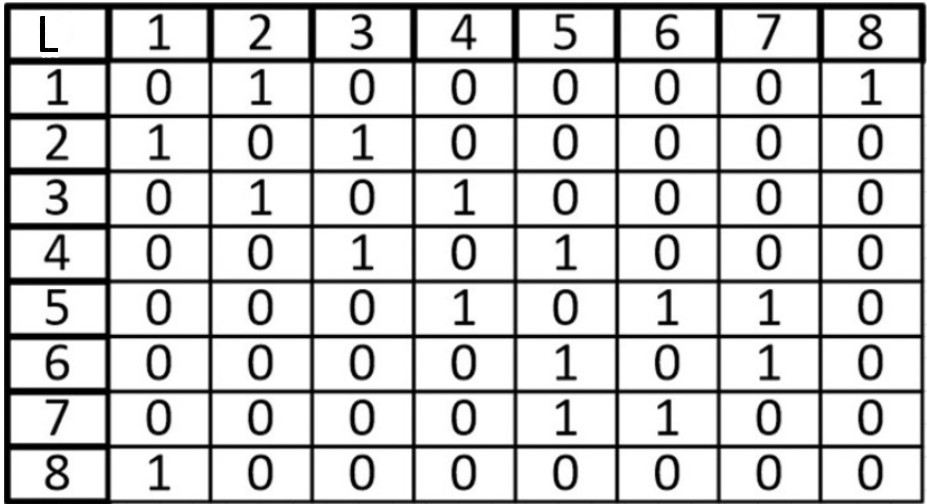
Ячейки, расположенные на главной диагонали всегда равны нулю, потому что ни у одной вершины нет ребра, которое и начинается, и заканчивается в ней только если мы не используем петли. То есть наша матрица симметрична относительно главной диагонали. Благодаря этому мы можем уменьшить объем памяти, который нам нужен для хранения.
С одной стороны объем памяти будет:
Но используя вышеописанный подход получается:
Потому что нижнюю часть матрицы мы можем создать из верхней половины матрицы. Только при условии того, что у нас главная диагональ должна быть пустой, потому что при наличии петель данное правило не работает.
Если граф неориентированный, то, когда мы просуммируем строку или столбец мы узнаем степень рассматриваемой нами вершины.
Если мы используем ориентированный граф, то кое-что меняется.
Здесь отсутствует дублирование между вершинами, так как если вершина 1 соединена с вершиной 2, наоборот соединена она не может быть, так у нас есть направление у ребра.
Возьмем в этот раз ориентированный граф и сделаем матрицу смежности для него:

В виде матрицы:

Если мы работаем со строкой матрицы, то мы имеем элемент из которого выходит ребро, в нашем случаи вершина 1 входит в вершину 2 и 8. Когда мы работаем со столбцом то мы рассматриваем те ребра, которые входят в данную вершину. В вершину 1 ничего не входит, значит матрица верна.
Объем памяти:
Если бы на главной диагонали была бы 1, то есть в графе присутствовала петля, то мы бы работали уже не с простым графом, с каким мы работали до сих пор.
Используя петли мы должны запомнить, что в неориентированном графе петля учитывается дважды, а в ориентированном - единожды.
Матрица инцидентности
Инцидентность – понятие, используемое только в отношении ребра и вершины: две вершины (или два ребра) инцидентными быть не могут.
Матрица (назовем ее I) состоит из n строк которое равно числу вершин графа, и m столбцов, которое равно числу ребер. Таким образом полная матрица имеет размерность n x m. То есть она может быть, как квадратной, так и отличной от нее.
Ячейка в позиции I (i, j) равна 1 тогда, когда вершина инцидентна ребру иначе мы записываем в ячейку 0, такой вариант представления верен для неориентированного графа.
Сразу же иллюстрируем данное правило:

В виде матрицы:
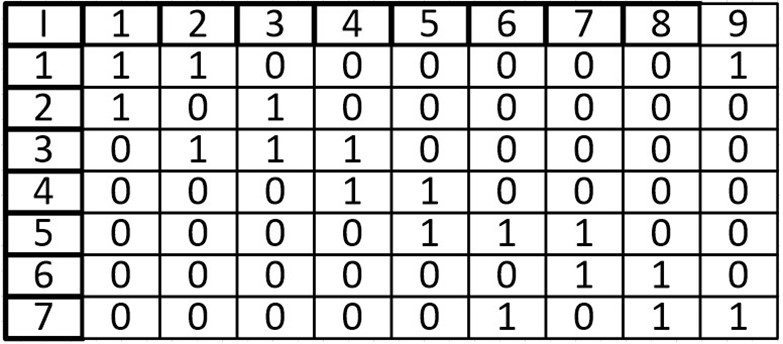
Сумма элементов i-ой строки равна степени вершины.
При ориентированным графе, ячейка I (i, j) равна 1, если вершина V (i) начало дуги E(j) и ячейка I (i, j) равна -1 если вершина V (i) конец дуги E (j), иначе ставится 0.
Ориентированный граф:
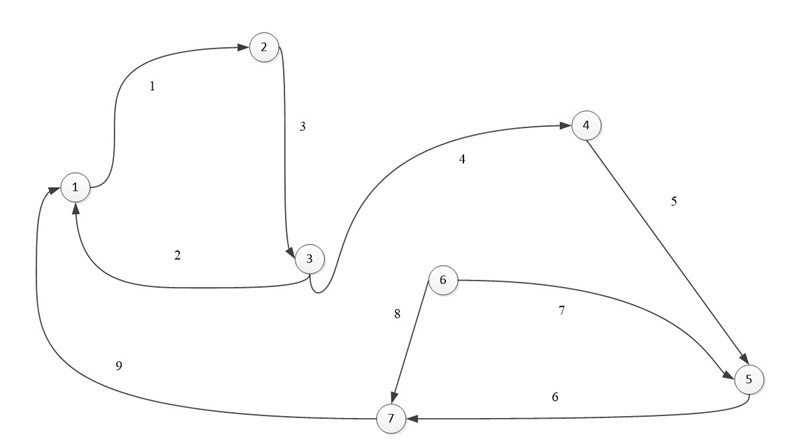
В виде матрицы:
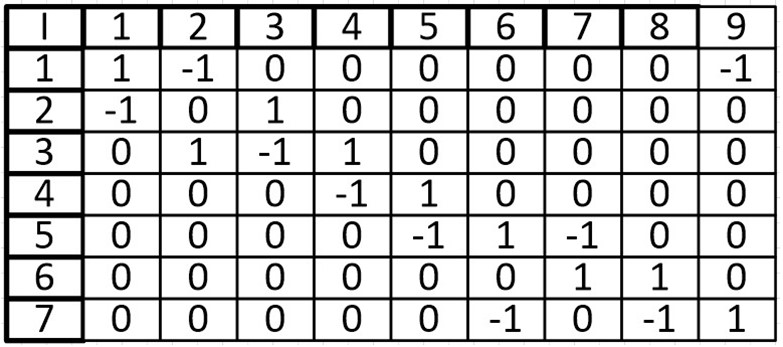
Одной из особенностей данной матрицы является то, что в столбце может быть только две ненулевых ячейки. Так как у ребра два конца.
При суммировании строки, ячейки со значением -1, могут складываться только с ячейками, также имеющими значение -1, то же касается и 1, мы можем узнать степень входа и степень выхода из вершины. Допустим при сложении первой вершины, мы узнаем, что из нее исходит 1 ребро и входят два других ребра. Это является еще одной особенностью (при том очень удобной) данной матрицы.
Объем памяти:
Список смежности (инцидентности)
Список смежности подразумевает под собой, то что мы работаем с некоторым списком (массивом). В нем указаны вершины нашего графа. И каждый из них имеет ссылку на смежные с ним вершины.

В виде списка это будет выглядеть так:
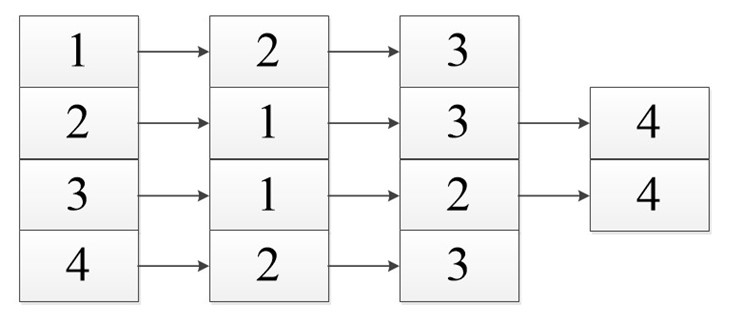
Неважно в каком порядке вы расположите ссылку так как вы рассматриваете смежность относительно первой ячейки, все остальные ссылки указывают лишь на связь с ней, а не между собой.
Так как здесь рассматривается смежность, то здесь не обойдется без дублирования вершин. Поэтому сумма длин всех списков считается как:
Объем памяти:
Когда мы работаем с ориентированным графом, то замечаем, что объем задействованной памяти будет меньше, чем при неориентированном (из-за отсутствия дублирования).
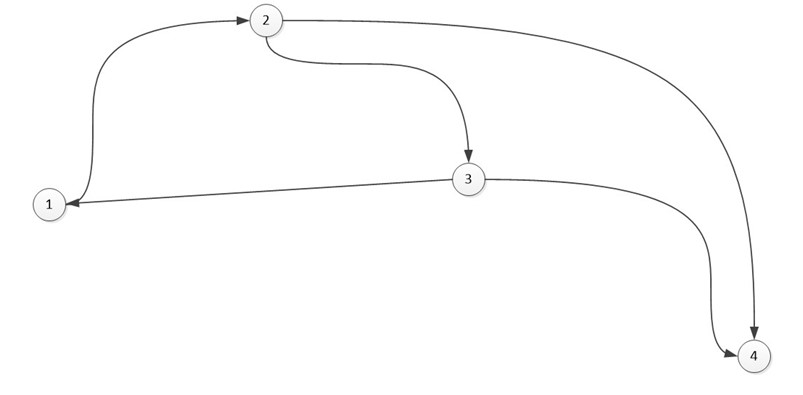
В виде списка:
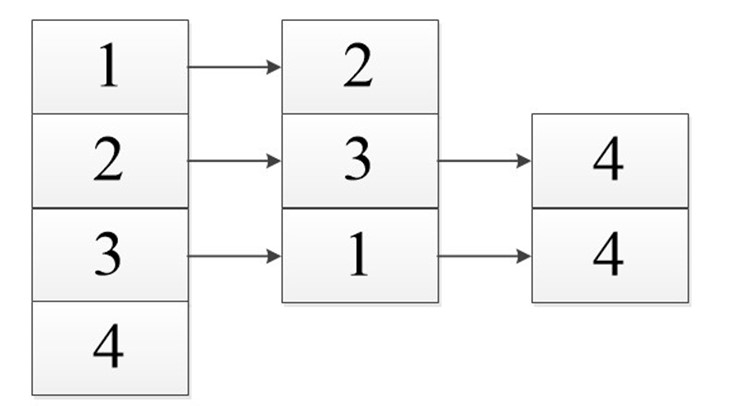
Сумма длин всех списков:
Объем памяти:
Со списком инцидентности все просто. Вместо вершин в список (массив) вы вставляете рёбра и потом делаете ссылки на те вершины, с которыми он связан.
К недостатку списка смежности (инцидентности) относится то что сложно определить наличие конкретного ребра (требуется поиск по списку). А если у вас большой список, то удачи вам и творческих успехов! Поэтому, чтобы работать максимальной отдачей в графе должно быть мало рёбер.
Взвешенность графа
Взвешенный граф - это граф, в котором вместо 1 обозначающее наличие связи между вершинами или связи между вершиной и ребром, хранится вес ребра, то есть определённое число с которым мы будем проводить различные действия.
К примеру, возьмем граф с весами на ребрах:

И сделаем матрицу смежности:
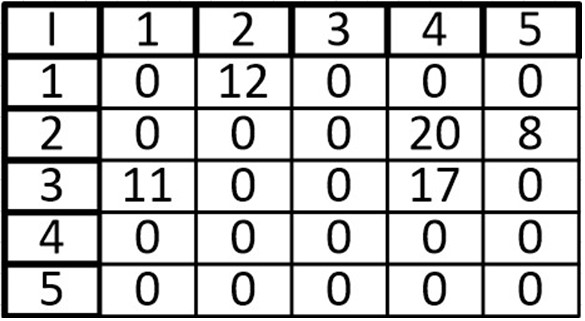
В ячейках просто указываем веса ребра, а в местах где отсутствует связь пишем 0 или -∞.
Более подробно данное определение будет рассмотрено при нахождении поиска кратчайшего пути в графе.
Итак, мы завершили разбор представления графа с помощью матрицы смежности и инцидентности и списка смежности (инцидентности). Это самые известные способы представления графа. В дальнейшем мы будем рассматривать и другие матрицы, и списки, которые в свою очередь будут удобны для представления графа с определёнными особенностями.
Если заметили ошибку или есть предложения пишите в комментарии.
Комментарии (19)

third112
31.07.2021 22:27Не понял:
в неориентированном графе петля учитывается дважды
Пусть в графе 4 вершины и только одна петля у вершины 1, других ребер нет, тогда м-ца смежности будет иметь 1 в первом элементе (1,1), все остальные будут нули.
Не понял список смежности для первого графа в секции. На рисунке ребро 1-4 кратное, и нет ребра 2-3. Если сделать ребро 1-4 не кратным, то список можно записать проще и экономнее: 1-2, 1-3, 1-4, 2-4, 3-4, всего 5 ребер. А по Вашему списку их больше. Список смежности часто употребляют для ручного ввода, это бывает быстрее, чем матрицу набивать.

Qfaz12 Автор
31.07.2021 23:16Касательно, списка смежности. Спасибо за найденный недочет вставил не ту картинку, уже все поменял. Касательно первого вопроса. У нас же неориентированный граф, и получается, что в вершине 1, ребро как выходит, но также и входит в него. И мы должны будем поставить 2, так как если мы захотим узнать степень вершины и как вы говорите поставим 1, то мы учтем только тот случай когда в нее входит ребро, но оно же из него и выходит, а это уже не будет учтено, что будет являться ошибкой.

third112
31.07.2021 23:44В Вашем подходе неориентированный граф — частный случай орграфа: ребро выходит из в-ны 1 и заходит в 2, и другое ребро из 2 заходит в 1. На рисунке это будет со стрелочками: 1 ->2, 2 -> 1 или 1 <->2. Но это избыточно. Во многих признанных учебниках орграфы идут отдельной главой — студенту бы просто графы понять, ему не до петель! Видимо, многие авторы таких учебников (Харари, Зыков и др.) сочли бы Ваш подход методологически ошибочным.

quwarm
01.08.2021 11:261. По поводу чисел в графах — они маленькие, а расстояния между вершинами большие. Возможно, у вас какая-то программа генерирует эти изображения. Рекомендую для статей использовать draw.io (там можно и перемещать объекты, и менять размер шрифта и др.).
2. «Но есть еще два способа как можно задавать граф, а точнее представлять его». Если можно написать точнее, то пишите без лишних слов.
3. Неправильные определения плотного и разреженного графов: «... плотных графов в которых количество ребер (E) примерно равно количеству вершин (V)» и «... разреженных графов, то есть графов где количество ребер меньше количества вершин». Откуда прямая связь с числом вершин? Плотный граф — граф, в котором число ребер близко к максимально возможному числу ребер (у полного графа) (см. определение из NIST). Разреженный граф — граф, в котором число ребер намного меньше максимально возможного числа ребер (у полного графа) (см. определение из NIST).
4. Множество орфографических, грамматических и логических ошибок.
Наиболее выделяющиеся ошибки
«Здесь отсутствует дублирование между вершинами, так как если вершина 1 соединена с вершиной 2, наоборот соединена она не может быть, так у нас есть направление у ребра». Конструкция «если ..., то» частично отсутствует.
«В вершину 1 ничего не входит, значит матрица верна». Это не вывод, вы же заранее составляете матрицу, а не доказываете её правильность.
«в нашем случаи». Должно быть «в <?> случае».
5. Перевёрнутую А не используют для обозначения матрицы. Матрицу обозначают буквой M (английской; от слова Matrix), иначе грош цена вашим обозначениям, когда они ни одному учебнику и ни одному стандарту не соответствуют.
Остальное не проверял — потерял интерес.
Теория графов хорошо проработана во многих учебниках. Не совсем понимаю, в чем смысл таких чисто теоретических статей, причем с ошибками. Желательно делать одну статью с краткой теорией и большей по объему практикой.
Upd. Также непонятно, что делает эта статья в хабах «Сетевые технологии», «Машинное обучение» и «Искусственный интеллект».

Qfaz12 Автор
01.08.2021 15:17Благодарю, поменял в тексте моменты, высказанные вами в виде замечаний.

PrinceKorwin
01.08.2021 15:18Подскажите, пожалуйста, какие материалы лучше почитать чтобы лучше понимать тему? Не только про сами графы, но и алгоритмы поверх него интересуют (dfs, bfs, поиск кратчайшего пути и т.д.).

quwarm
01.08.2021 16:37Из классики на русском — «Фундаментальные алгоритмы на C++. Часть 5. Алгоритмы на графах» Роберта Седжвика и «Совершенный алгоритм. Графовые алгоритмы и структуры данных» Тима Рафгардена.
На английском можно найти больше книг. Можно посмотреть в сторону Amazon (в поиске есть фильтры, в том числе фильтр по целевой аудитории + отзывы развернутые). Там нужно именно выбирать книги по отзывам, а скачивать — на Libgen или на Z-Library.

PrinceKorwin
01.08.2021 19:20Спасибо большое!

third112
02.08.2021 18:54Классическая книга это:
Кристофидес, Теория графов. Алгоритмический подход, М.: Мир, 1978 (м.б. есть болеее новые переиздания).
Еще:
В.Липский, Комбинаторика для программистов, М.: Мир, 1988.
И объемный том:
В.Н.Касьянов, В.А.Евстигнеев, Графы в программировании: обработка, визуализация и применение, Спб: БХВ-Петербург, 2003.


amarao
Мне кажется, одна из серьёзных проблем любой статьи про графы в том, что после "введения в графы", когда даётся 2-3 примера, дальше всё вываливается сухим потоком.
Если бы каждый случай разбирался "из практики" (ну вот где у вас плотные графы на существенные размеры бывают? Я вот с ходу и придумать не могу), да ещё и с описанием "плохих" попыток, то наглядность была бы значительно выше.
third112
Согласен. Сожалею, что не могу голосовать.
Qfaz12 Автор
Думаю, что да. Люди бы более яснее понимали, почему лучше использовать именно этот метод и тд. Возможно в последующих статьях я попытаюсь сделать, что-то подобное. Наверное это будет очень не скоро, но пока все что есть. Здесь я попытался в максимально доступной форме объяснить, как же это делать. И в первую очередь я делаю это для студентов, которые изучают данную тему и могут не понимать, зачем вообще графы нужны. Учась, я лично убедился, что для многих эта тема была "проходной" и они не извлекли из нее никакой ценной информации, а также так и не поняли, как работать с матрицами.
third112
ИМХО для IT-студентов нужно сразу сказать, что списки (стеки, очереди) и бинарные деревья это графы. И всякие схемы, типа схемы метро, автодорог, принципиальные в электронике можно рассматривать как графы. Приложения теории графов — это фундаментальные свойства всяких подобных схем.
Для студентов историков м.б. будет полезно узнать, что фамильные деревья — это графы. И проч. др. специальности. Где только нет графов, пусть на уровне тривиального списка. Возвращаясь к IT: строка символов — граф. и число — последовательность байт — граф, и файл — граф, не говоря о БД.
Qfaz12 Автор
Вы знаете, не все учителя преподающие в учебных заведениях, могут обладать столь широкими познаниями в графах, также теория графов, к сожалению только одна из тем в большом предмете под названием дискретная математика и не многие учителя могут раскрыть эту тему полностью, из-за нехватки времени.
Также хочу отметить, что наша беседа описанная чуть ниже не приведет к конкретным выводам так как сама теория графов очень неоднородна и у каждого человека свои мнения, тоже касается и авторов. Делая статьи я не придумаю каких-либо правил, а использую имеющиеся у меня ресурсы для того, чтобы создать статью удовлетворяющую все стороны (ну или постараться это сделать). Следуя этому ваше сообщения, где как кажется вы подчеркнуто выделили "Ваш подход" выглядит неуместно и честно не слишком приятно. Создавая статьи, я также использую учебник Харари. То о чем вы говорите находится у него отдельной темой "Орграфы" и подзаголовок обозначен там, как "Орграфы и матрицы" я читал этот раздел и отдельно главу про матрицы, но для статьи решил ничего оттуда не брать и обратится к другим источникам, где нашел описанную мною информацию. Это не значит, что мне нравится его формулировка, это значит, что я выбрал в качестве описание, отличное от него в некоторых аспектах описание. И думаю, что на этом наше противоречие стоит остановить, ибо мы уже итак нарушили закон логики, но также не сможем выявить чье мнение истинно, так как оба заслуживают жизнь. Спасибо за замечания и высказанную точку зрения!)
third112
Совершенно с Вами согласен. Преподаватели непрофильных для вуза предметов часто не имеют представления об интересах студентов, которых учат. Вспоминаю, что на 5 курсе ХФ МГУ к нам пришла молодая девушка, почти нашего возраста, учить нас английскому. Она рассказала нам, что только что закончила иняз, и диплом у нее был по Шекспиру. Язык она знала очень хорошо, но не химический. А химию она не знала — со школы успела забыть, что знала. А у нас были методички с текстами из научных хим. журналов. Думаю, что это было большое упущение нашего деканата: на факультете было много химиков, которые хорошо владели английским. Нужно было к таким учителям английского, как наша девушка, приставить консультантов, которые бы помогали в переводе хим.текстов и, что самое важное, объясняли на русском хим. смысл. Аналогично с учителями дискретной математики. Каждый человек приходя на новую работу должен изучить специфику. Лектор, который чисто формально читает студентам теорию графов и не думает об адресации, поступает плохо. Мог бы сам в деканат обратиться с просьбой дать консультанта.
У лектора должно быть время на подготовку, которое ему оплачивают, как и лекцию. Если лектор еще где-то работает по совместительству, то это его выбор — придеться перерабатывать.
Честно: очень сожалею, о том, что показалось Вам не приятным. Правда, я не понял, какие именно слова Вам не приятны. Если про методологию, то с моей стороны это был скорее вопрос, а не утверждение. Я привел пример иных методологических подходов и ожидал от Вас услышать обоснование Вашего. Это наука, и ничего личного. Если кто-то напишет, что дважды два пять, и я спрошу: нет ли у Вас здесь ошибки? А он ответит, что я задал не приятный вопрос. Думаю, что всем участникам обсуждения станет не очень приятно.
Я не могу назвать его своим подходом, т.к. его придумали до меня, и я указал на авторов. Но принимаю Ваш вывод:
Спасибо!