"Графы являются одним из объединяющих понятий информатики – абстрактное представление, которое описывает организацию транспортных систем, взаимодействие между людьми и телекоммуникационные сети. То, что с помощью одного формального представления можно смоделировать так много различных структур, является источником огромной силы для образованного программиста". Стивен С. Скиена

В этой статье:

• Введение

• Классификация графов

Введение

Сначала под землей города Москвы ничего не было. Потом была построена первая станция метро, а затем и вторая и третья. Образовалось множество станций метро. На карту было занесено множество точек. Позже между станциями стали прокладывать пути линии. И соединилась станция метро А со станцией метро Б. Все остальные станции также стали соединятся друг с другом и на карте появилось множество линий. В итоге мы имеем Московский метрополитен очень красивый, я там был проверял.

Посмотрите какая красота. У нас имеется множество точек (которые называются вершинами или узлами), а также множество линий (называемые рёбрами или дугами). Обозначим множество вершин буквой V от английского vertex?вершина и множество рёбер обозначим E от английского edge?ребро. Граф в формулах именуют буквой G. Все вершины обязательно должны быть идентифицированы.

Отмечу, что число вершин обозначается буквой n:

Число рёбер обозначается буквой m:

Таким образом граф задается и обозначается парой V,E:

Граф - это совокупность пары множеств. Конечного есть и бесконечные, однако мы их пока не рассматриваем непустого множества V и множества E заданного неупорядоченными парами множества V.

Также определение графа рассказывается в этой статье на Хабре (https://habr.com/ru/post/65367/)

Неформально граф является совокупностью точек и линий. Линии в котором задаются парой вершин, расположенных не важно в каком порядке.

Разберем определение графа подробней. Может ли в G быть пустым множество E? Да без проблем! Такой граф будет называться нулевым, а вершины в нем будут называться изолированными.

Только вот множество V вершины пустым быть не может. Ведь множество E рёбра задается парой неупорядоченных вершин множества V. Две вершины образующие ребро, называются концами этого ребра.

Множество E задается парой неупорядоченных вершин множества V.

Пример: Пусть множество V = {1,2,3,4,5}. Тогда множество E = {1,2, 2,3, 3,4, 1,5, 1,4, 3,1}

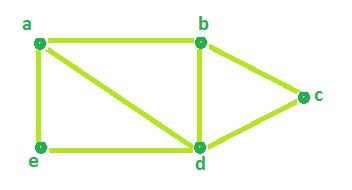
Граф будет выглядеть следующим образом:

Висячей вершиной называется вершина которая соединена только с одной соседней вершиной. В нашем случаи висячей вершиной будет вершина 5, так как она соединена только с вершиной 1.

Степенью вершины - является количество рёбер исходящих выходящих из вершины и входящих в нее. Данное определение верно для ориентированных графов см. классификацию графов. Для неориентированных графов исходящая степень равна входящей. Степенью вершины 1 будет является число 4. Так как вершина 1 соединена с вершиной 2, 3, 4, 5.

Степень записывают, как:

Максимальная степень, то есть какое количество степеней вообще присутствуют в графе обозначаются, как:

Минимальную как:

Формула суммы степеней для G = V,E выглядит так:

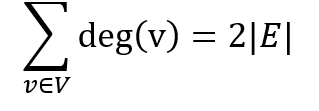
То есть сумма степеней всех вершин v графа равна удвоенному количеству его рёбер E. Считаем количество степеней в нашем примере. От этого никуда не денешься. Я насчитал 12. А теперь считаем, сколько у нас рёбер. Их 6! Умножаем на 2 и получаем 12. Совпадение? Не думаю!

А давайте представим наш граф в другом виде, но с сохранением данных пар. G теперь имеет следующий вид:

Заметьте я не изменил пары между собой. Вершина 4 также соединяется с вершиной 3, а у вершины 1 степень также осталась 4. Так почему граф имеет совершенно другой вид и законно ли это?

Самое главное в графе это вершины и проведенные между ними рёбра. В связи с этим граф является топологическим объектом, а не геометрическим . То есть объектом который не меняется при любых растяжениях и сжатиях. Нам все равно какой мы сделали отрезок. Кривой, прямой, самое главное это наличие связи между вершинами. По этой причине графы являются очень универсальными в плане практического применения. Мы можем обозначать ими дороги, компьютерную сеть, людей которые дружат друг с другом или даже влюблены друг в друга.

Классификации графов

• Первым признаком классификации является отсутствие или наличие ориентации у ребер.

  Ребро является неориентированным если у него нет понятия начала или конца. То есть оба его конца равноправны. Такой граф называется неориентированным, обыкновенным или неографом.

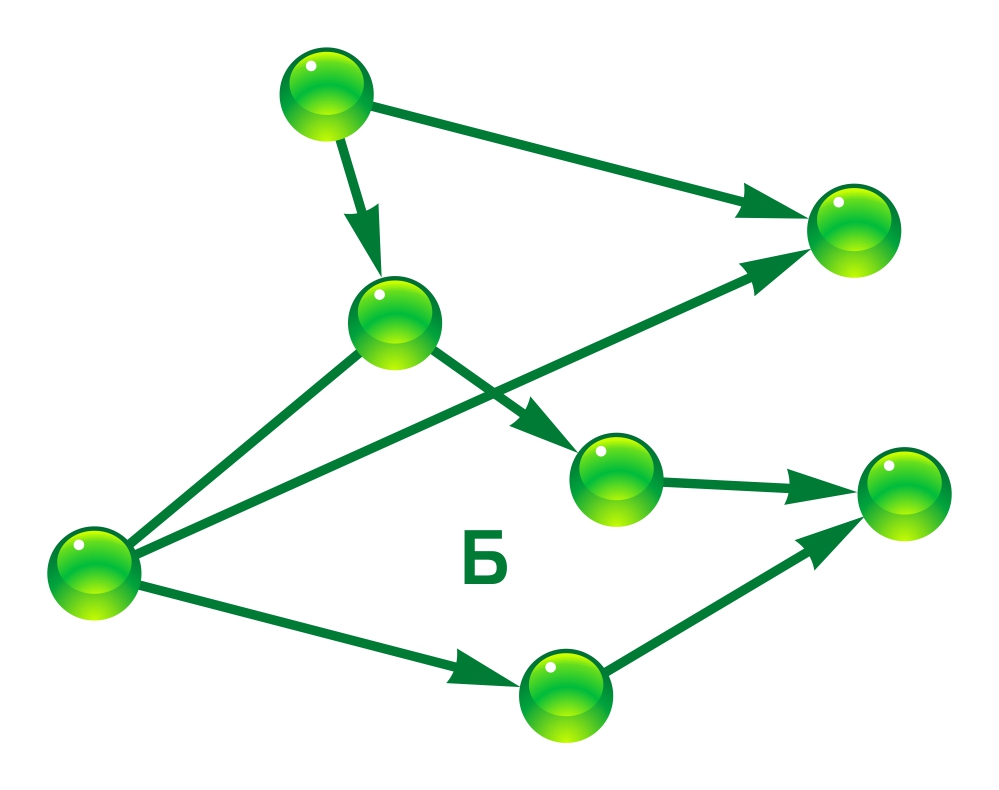
Ориентированное ребро обозначается стрелкой. И указывает ориентацию от вершины к вершине. То есть данный граф имеет начало и конец. И называется он ориентированным или орграфом.

Также существует граф со смешанными ребрами. Это когда в графе присутствуют, как ориентированные рёбра, так и неориентированные.

• Вторым признаком является отсутствие или наличие кратных ребер.

  Кратные ребра - это ребра которые встречаются между двумя вершинами сразу несколько раз. В примере ниже мы видим, что вершина a соединена с вершиной c несколько раз. То же самое происходит и a c b. Такой граф называется мультиграфом.

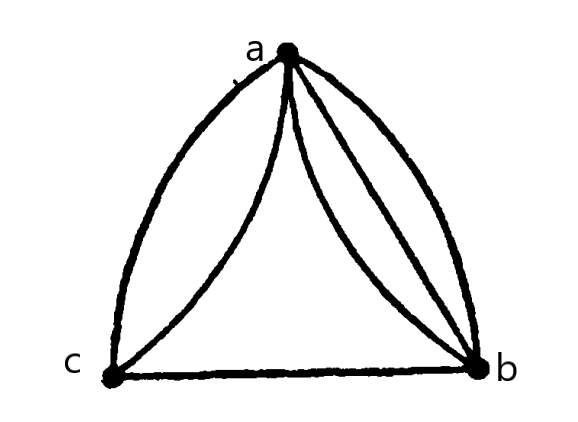
Граф в котором кратных ребер нет, является простым графом. В простом графе мы просто называем пару вершин для идентификации ребра, но в мультиграфе такое уже не сработает, так как одна и та же пара вершин будет указывать на два ребра и не понятно что к чему будет относится. Поэтому если вы повстречаете мультиграф, то вы должны обозначить каждое ребро отдельно.

Заключение

В данной стать я не рассмотрел, понятия смежности и инцидентности, однако я решил их рассмотреть в следующий раз. Также хочу отметить, что более подробно виды графов, я буду рассматривать в следующих статьях. Если у вас есть вопросы, предложения или я где-то допустил ошибки, то прошу написать их в комментариях.