Вы устали преобразовывать координаты в трёхмерном пространстве с помощью матриц вращений и прочих кватернионов? Я прекрасно Вас понимаю, и сам провёл не один час своей жизни за этим утомительным занятием. Но, похоже, Вашим и моим мучениям пришёл конец – мне удалось обнаружить простой и наглядный метод, позволяющий значительно упростить эту непростую задачу.
Собственно говоря, для начала обратим внимание на всем известную декартову систему координат (лично я по старой привычке называю её «нормальной»). Она, как известно, связана с экваториальными координатами светил простыми соотношениями:
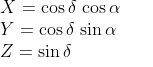
А вот и изображение для наглядности:

Пока всё знакомо, правда?
А теперь переходим к тому, что, собственно, и представляет из себя новизну. Допустим, у нас есть декартовы координаты, и по ним нужно вычислить экваториальные или даже эклиптические координаты. Что обычно происходит? Скучная и кропотливая работа, в которой многие делают ошибки – добро пожаловать к расчётам с функцией tan2 c большим количеством условий. Однажды мне всё это надоело, а точнее, я устал от этого, и я придумал способ, с помощью которого, зная всего три значения X, Y и Z, можно безошибочно определить углы экваториальной или эклиптической систем с помощью следующего алгоритма:

Не торопитесь снисходительно улыбаться и мысленно похлопывать меня по плечу: дескать, фантазёр ты, приятель, куда тут без tan2… Но я многократно проводил подобные расчёты в Excel, и метод действительно прекрасно работает, каким бы странным это ни казалось на первый взгляд. Не нужно только забывать переводить градусы в радианы, а радианы в градусы там, где это необходимо. Взгляните сами:
α |
δ |
X |
Y |
Z |
α* |
δ* |
0 |
30 |
0.866 |
0.000 |
0.5 |
0 |
30 |
30 |
30 |
0.750 |
0.433 |
0.5 |
30 |
30 |
60 |
30 |
0.433 |
0.750 |
0.5 |
60 |
30 |
90 |
30 |
0.000 |
0.866 |
0.5 |
90 |
30 |
120 |
30 |
-0.433 |
0.750 |
0.5 |
120 |
30 |
150 |
30 |
-0.750 |
0.433 |
0.5 |
150 |
30 |
180 |
30 |
-0.866 |
0.000 |
0.5 |
180 |
30 |
210 |
30 |
-0.750 |
-0.433 |
0.5 |
210 |
30 |
240 |
30 |
-0.433 |
-0.750 |
0.5 |
240 |
30 |
270 |
30 |
0.000 |
-0.866 |
0.5 |
270 |
30 |
300 |
30 |
0.433 |
-0.750 |
0.5 |
300 |
30 |
330 |
30 |
0.750 |
-0.433 |
0.5 |
330 |
30 |
360 |
30 |
0.866 |
0.000 |
0.5 |
360 |
30 |
Что происходит дальше? Мне нужно найти эклиптические координаты, то есть перейти к системе координат, которая всё ещё является декартовой, но уже «повёрнутой» (опять же по привычке называю её именно так).
Осуществить это будет совершенно не сложно.
Выполним преобразование декартовых векторов, используя известные формулы.
Преобразование эклиптических координат в экваториальные координаты:
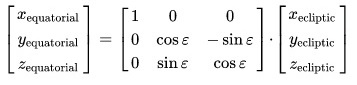
Преобразование экваториальных координат в эклиптические координаты:

Когда получаем в итоге тройку декартовых эклиптических координат, просто обращаемся к алгоритму, описанному выше, и получаем эклиптические координаты светила λ и β (вместо α и δ). Вот, собственно говоря, и всё. Заинтересовались? А теперь попробуйте сами и убедитесь.
Комментарии (7)

Refridgerator
05.11.2021 08:34Кватернионы в экселе действительно считать сложновато. Но если взять более подходящий инструмент, то и считать самому ничего не придётся — можно просто перемножать кватернионы и всё. А то, что арктангенс можно выразить через арккосинус — мягко говоря, не новость.

a-tk
05.11.2021 10:24А что нового-то?
У Пфлегера и Монтенбрука вычисления через матрицы через всю книгу шли ещё с первого издания книги.


aamonster
Э... В чём новизна-то? Все давно знают этот подход, это один из первых вариантов преобразования, которые пишет новичок. Уже потом он узнаёт про arctan2, который позволяет не считать корень, не проверять особые случаи и реализован в сопроцессоре начиная с 8087. А потом узнаёт, что преобразовывать в сферическую систему координат вообще не надо, и в виде векторов и матриц (или кватернионов) всё гораздо проще.
Ingus71 Автор
Могу я поинтересоваться в какой книге описан алгоритм, в котором углы преобразуются в углы, а не в тангенсы или синусы?
К тому же, меня прельстил высокий потенциал для понимания сути процесса именно матричных поворотов пространства. Одно дело выучить формулу, другое - уметь её вывести.
aamonster
Прошу прощения, я был невнимателен и сконцентрировался на основной (и самой сложной) части преобразования – от декартовых координат к сферическим.
И, соответственно, говорил именно про формулу этого преобразования, выводимую новичком. Он может выбрать любую из обратных тригонометрических функций. Это позже узнает, какие решения принято использовать для этой задачи (и в идеале – почему).
У арккосинуса, кстати, есть ещё один недостаток: крайне нехорошее поведение в районе ±1 (производная стремится к нулю), там большая погрешность. arctan2 лишён этого недостатка.
Само вычисление через промежуточные декартовы координаты кажется абсолютно естественным, в голову бы не пришло выписывать одни синусы через другие.
ЗЫ: Стремление вывести формулы самостоятельно всячески поддерживаю. Лучше их понять, чем запомнить (лично мне и легче тоже).
Ingus71 Автор
Я прошелся в околополярном районе, где X и Y близки к нулю. И всё работает как часы. Буду благодарен Вам, если Вы укажете такие X и Y, при которых начинается "крайне нехорошее поведение" и вылезает погрешность, т.е. фокус с преобразованием Альфа и Дельта в X,Y,Z и обратно не приведет к исходным Альфа и Дельта.
aamonster
Y около 0, X около 1. Погрешность в 10-м знаке X после запятой даст вам погрешность в пятом знаке альфа.
Может, конечно, в вашей задаче это и неважно. Но лучше такого избегать, если бесплатно :-) (а atan2(Y,X) – это не то что бесплатно, это даже дешевле, чем if + корень + деление + арккосинус).