Описание проблемы

В компьютерной графике принято понимать под текстурой любое изображение, применяемое в реализации сцены. В теории цифровой обработки изображений текстуры это случайные поля. В данной статье рассматриваются случайные поля и способы из описания. Случайное поле есть функция F(x,y), значениями которой являются случайные величины. Если предполагается использовать значения этой функции в качестве генератора текстуры, то на значения поля накладываются дополнительные ограничения:

• Все случайные величины z поля имеют одно и то же распределение.

• Ковариация между F(x₀,y₀) и F(x₁,y₁) зависит только от вектора, соединяющего точки ( x₀,y₀) и (x₁,y₁) . (стационарность)

Важность выполнения указанного свойства случайного поля вытекает из следующей гипотезы.

Восприятие случайного поля человеком зависит только от значений ковариаций.

Не существует математического (статистического) доказательства справедливости данной гипотезы, но в практических исследованиях она считается выполненной.

Проблема состоит в разработке метода, с помощью которого можно получить текстуру с предписанной ковариационной функцией. Такая задача возникает, например, при отладке программ распознавания объектов, существенной характеристикой которых является случайная текстура (лес, поле, водная поверхность). Ограниченное применение эти текстуры имеют в компьютерной графике. Соответствующая ссылка приведена в конце статьи.

Генерация стационарной текстуры

В этй статье мы пользуемся терминами "корреляция" и "ковариация". Разница заключается в том, что при вычислении последней не предполагается нормировка дисперсий случайных величин, и их центрирование не считается обязательным.

Известен следующий простой способ генерации случайных полей. Пусть задана матрица A , элементы A[x,y]=z_x,y которой есть некоррелированные случайные величины с одинаковым распределением и нулевым средним. Это означает, что математическое ожидание

• E(A[x,y]A[x',y']) =0, если есть отличия хотя бы в одном из индексов.

• E(A[x,y]A[x,y]) =S, где S от от индексов не зависит.

Выберем произвольную вещественную матрицу B размера M X N , размер которой значительно меньше размера матрицы A и построим матрицу

Найдем ковариацию двух позиций в матрице F

В полученной сумме отличные от нуля слагаемые лишь те, в которых x+i=x'+j' и y+j=y'+j' . Это означает, что

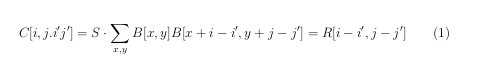
Из (1) следует, что полученное поле обладает свойством стационарности -- ковариация между двумя позициями зависит только от вектора, соединяющего позиции этих точек.

Ниже приводится скрипт для создания текстуры согласно изложенному методу и

import numpy as np
from scipy import signal as sgn
from numpy.random import random
from matplotlib import pyplot as plt


def getImg(Ax,Ay,B):
    A=random((Ax,Ay))-0.5
    C = sgn.correlate2d(A,B,mode='same')
    plt.imshow(C,cmap='gray')

два примера текстур, построенных с помощью матриц B1,B2

B1 = np.float_([[1,2,4],[-1,4,1],[2,0,3]])
B2 = np.float_([[-3,2,1],[1,-5,-1],[-3,0,0]])

Fig.1 Текстуры, построенные по матрицам В1 и В2

Согласно определению, значения функции R(p,q) в (1) не зависят от знака аргумента, поэтому можем считать эти аргументы неотрицательными числами. Теоретические значения этой функции находятся с помощью скрипта

Coe=1/12
def findR(B,P,Q):
    ''' Covariation Cov(P,Q)
    '''
    M,N = B.shape
    if P>=M or Q>=N:
        return 0
    
Matr1 = np.zeros((M+P,N+Q))
Matr1[:M,:N] = B
Matr2 = np.zeros((M+P,N+Q))
Matr2[-M:,-N:] = B
return Coe*np.sum(Matr1*Matr2)

Здесь Coe зто S в (1). Величина 1/12 находится как дисперсия случайное величины с равномерным распределением на интервале [-0.5,0.5]. Результаты подсчёта ковариаций для указанных матриц В приведены в таблицax 1,2.

Легко видеть, что различаются как текстуры, так и матрицы ковариаций.

Частичное решение проблемы создания текстуры по матрице ковариаций

В общем случае решить уравнения (1) относительно элементов матрицы В можно лишь приближённо и не очень понятно, как это сделать. Рассмотрим частный случай, когда матрица В состоит из одинаковых строк D длины M -- D=d[0],d[1],.., d[M-1]. В этом случае элементы разных строк матрицы С не коррелируют, поэтому достаточно рассмотреть корреляции лишь в одной стоке этой матрицы. Уравнения (1) принимают вид (2)

Способ отыскания коэффициентов d[k] в (2) был предложен Фейером (L.Fejer) более 100 лет тому назад. Пусть

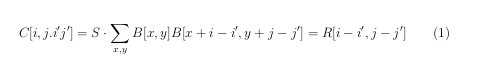
Тогда

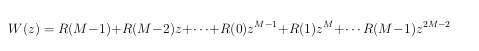
Здесь множитель S не играет роли. После этого находим все корни многочлена W(z) и оставляем только те из них, которые лежат внутри единичного круга. Проблемы возникают, если существуют корни на единичной окружности. По корням внутри единичной окружности восстанавливаем многочлен U(z) с точностью до нормировки. Коэффициенты найденного многочлена после умножения на нужный множитель составляют решение задачи.

Теперь алгоритм решения задачи о приближенном создании текстуры по заданным значениям R(P,Q) имеет следующий вид:

• По значениям R(0,0),R(0,1),...,R(0,N-1) находим строку D1 в.

• По значениям R(0,0),R(1,0),...,R(M-1,0) находим столбец D2 в.

• Подсчитываем M X N матрицу B =D2* D1 и применяем изложенный выше способ генерации текстуры

Применим этот метод к элементам Таблицы 1. Многочлен W(z) имеет коэффициенты 0.75,0.84,4.33,0.84,0.75. Находим корни многочлена с помощью функции numpy.roots. Два корня лежат внутри единичного круга, с помощью функции np.poly находим коэффициенты многочлена U(z) . Эти коэффициенты надо умножить на нормирующий множитель L с тем, чтобы произведение старшего и младшего коэффициентов равнялось 0.75. В результате получим вектор D1 = 2.02, 0.35, 0.37] (расположение коэффициентов по возрастанию или убыванию степеней значения не имеет). Аналогично найдём вектор D2 =1.95, 0.39, 0.60, используя первый столбец из Таблицы 1. Текстура, порождённая этими векторами, представлена на Fig.2

Fig.2 Текстура, построенная по одномерным векторам

Внешне она не отличается от оригинала.

Пример использования текстуры для изображения асфальта в ролике можно найти здесь /a>