Описание проблемы

Несанкционированное использование чужих медиа файлов является чумой 21 века. Законы, охраняющие авторское право, строги, и наказание (финансовое) за нарушения весьма существенное. Вся проблема заключается в трудности обнаружения преступления и в доказательстве авторских прав. Это две разные задачи, поэтому остановимся на них более подробно. В качестве примера ограничимся случаем музыкальных файлов. Получив доступ к файлу с записями, нарушитель, прежде всего, старается изменить его, не ухудшая потребительские качества продукта.

Типичными приёмами из арсенала пирата являются:

• Пропуск через специальный линейный фильтр

• Изменение частоты стробирования записи

• Манипуляции с отдельными фрагментами файла

• Применение сжатия файла с потерями

Найдя своё трансформированное произведение, автор его узнает без труда. За некоторыми исключениями не понятно, где искать свою собственность, поэтому речь может идти только об автоматическом поиске. Очевидно, что прямое сравнение искажённых копий с образцом не имеет смысла. В данной статье мы рассмотрим один из способов сравнения файлов устойчивых к отмеченным преобразованиям.

Второй этап наказания нарушителя начинается после обнаружения повреждённой копии и хозяина этой копии. Новый хозяин вполне резонно может заявить, что его файл является оригиналом, а человек, претендующий на авторство, украл оригинал, исказил его, а теперь требует компенсацию. В этом случае правда может быть установлена либо обращением к нотариусу,хранящему чистую копию, либо применением водяных знаков, внедрённых в оригинал. Эти знаки сохраняются в той или иной форме после манипуляций с файлом, и они могут быть извлечены с помощью алгоритма, известного только автору оригинала. Этой второй задачей мы не будем заниматься в данной статье.

Спектр сигнала и линейное предсказание

В настоящее время является общепризнанным фактом, что восприятие звука человеком определяется спектром сигнала. Простейшее решение автоматического поиска выглядит так. В оригинале выделяем фрагмент Fragm с помощью меток времени. В проверяемом файле находим Fragm1 по известным временным меткам и сравниваем спектры. В случае близости полученных результатов переходим к более подробному исследованию обнаруженного файла. Вот так выглядят спектры двух фрагментов: оригинального и того же фрагмента, пропущенного через фильтр низких частот.

Fig.1 Спектр сигнала (Spec) и спектр сигнала после фильтрации (FSpec)

Очевидно, что поточечное сравнение двух спектров вызовет несомненные трудности. Во втором случае высокие частоты подавлены, различить фрагменты на слух трудно, но сами векторы отличаются существенно. Чтобы обойти и возникшие трудности, обратимся к линейному предсказанию (ЛП), или linear prediction coefficients (lpc) Напомним теорию ЛП и проблемы, возникающие с применением метода на практике.

Элементы теории ЛП

Линейное предсказание хорошо известно в теории цифровой обработки сигналов. Здесь мы напомним основные определения, чтобы сохранить замкнутость изложения. Имеется случайный процесс y[n] . Смысл линейного предсказания заключается в возможности оценить следующее значение y[n], если известны k предыдущих значений процесса. Предполагается, что выполнены следующие условия в терминах математического ожидания E

Fig.2 Основные предположения в теории линейного предсказания

Сделаем несколько пояснений к приведённым "/? Обнаружение звукового файла после ''тюнинга '' с помощью линейного предсказания формулам. Формула (2) означает, что взаимная корреляция двух сигналов R(p) зависит только от разности аргументов. Число k в (3) известно заранее, а из (4) вытекает, что сигналы r[n] для разных аргументов являются некоррелированными. При сделанных предположениях коэффициенты предсказания находятся в виде решения линейной системы уравнений (5) где матрицы и векторы определены в (4)

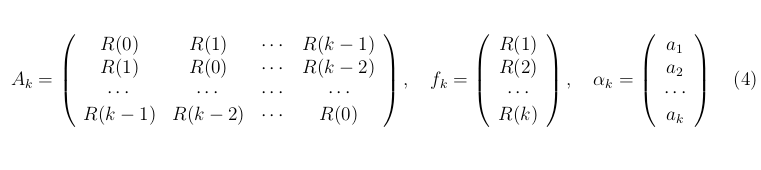
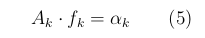
Fig.3 Система уравнений для отыскания коэффициентов предсказания

Известны рекуррентные формулы, позволяющие решить систему уравнений (5), не прибегая к обращению матрицы.

Кроме того, математическое ожидание преобразования Фурье от исходного процесса имеет вид

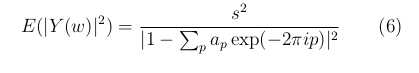
Fig.4 Формула для преобразования Фурье через ЛП

Значение константы s в (6) не используется в дальнейших рассуждениях.

ЛП в реальной ситуации

Посмотрим, как применяется теория ЛП для исследования конечных фрагментов звукового файла. Вместо математического ожидания вычисляется среднее значение. Единственное согласованное с теорией условие, которое может быть выполнено, это (1). Для этого достаточно вычесть из каждого значения y[n] среденее значение всех сигналов. Стационарность (2) справедлива для малых интервалов времени. Имеются проблемы при оценке R(p) , поскольку для разных p будет присутствовать разное число слагаемых в сумме для получения этой оценки. Значение k подбирается экспериментально, процесс r[n] есть результат линейной фильтрации исходного сигнала, поэтому можно говорить лишь об уменьшении дисперсии этого сигнала по сравнению с исходным сигналом. Тем не менее, решая систему (5), можно получить какие-то числа. Одно из таких решений представлено в пакете audiolazy , и мы будем пользоваться этим решением в дальнейших экспериментах. Из сказанного выше следует, что в реальных условиях большая часть предположений теории не имеет места. Однако были попытки использования полученных коэффициентов предсказания для сжатия аудио файлов и в программах распознавания речи. Сейчас для этих целей используют другие технологии, однако формула (6) нашла применение в задачах аналогичных рассматриваемой в этой статье. Прежде всего покажем на примере, что в некоторых случаях можно получить точную оценку спектра для неслучайных величин.

Ниже представлены все модули и функция, используемые при вычислениях

import numpy as np
from scipy.io.wavfile import read,write
from scipy.fftpack import fft
from scipy import signal as sgn
from audiolazy import lpc
from pydub import AudioSegment as asgm
from matplotlib import pyplot as plt

def getLpcSpec(Fragm,Ord=13):
    filt = lpc(np.float_(Fragm),Ord)
    Coef = np.float_(filt.numerator[:])
    U,V= sgn.freqz(1,Coef)
    AV = abs(V)
    AV /= np.linalg.norm(AV)    return AV

Функция freqz производит вычисления согласно (6), функция getLpcSpec возвращает нормированную версию спектра, вычисленного по формуле (6). Размер вектора, возвращаемого данной функцией, равен 512. Он не зависит от длины фрагмента и значения параметра Ord . Нормировка нужна для сравнения двух спектров с помощью скалярного произведения ( косинуса угла между векторами). Еще следует отметить выбор значения для Ord=13 . Это параметр k в (3). Выбор такого значения, в какой то мере, стал традиционным, хотя не является обязательным.

Результаты экспериментов

Прежде всего покажем, что в некоторых случаях (6) приводит к точному результату.

Ln = 2*512    
Arg = np.arange(0,Ln)
Fragm =  np.sin(2*np.pi*100*Arg/Ln)
Fragm -= np.mean(Fragm)
FFragm =  fft(Fragm)[:len(Fragm)//2]
plt.plot(abs(FFragm))
plt.figure()
Av = getLpcSpec(Fragm,Ord=13)
plt.plot(Av[3:])

Например, когда сигналом является синус, результаты вычисления спектров с помощью данного фрагмента показаны на рисунках

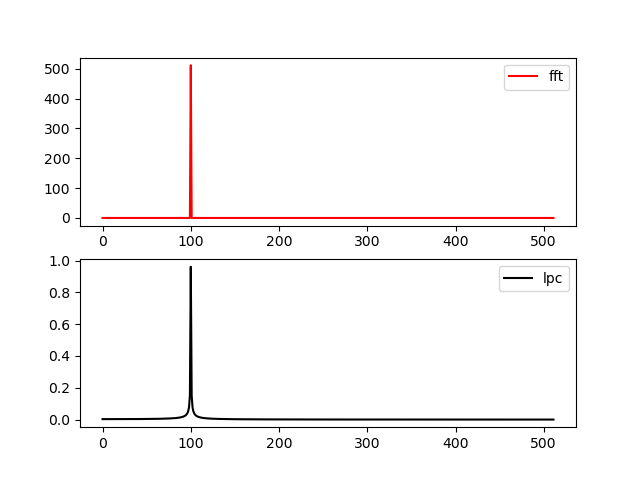
Fig.5 Вычисление спектра с помощью FFT (fft) и ЛП (lpc)

Длина сигнала выбрана специальным образом, чтобы всплески на обоих графиках были в одинаковых точках, отвечающих максимумам спектра. Для других длин нужен пересчёт положения точек с всплесками.

В случае произвольного сигнала такого совпадения не происходит. Вместо этого с помощью ЛП получаем сглаженный спектр.

Fig.6 Сравнение спектров, найденных с помощью FFT (fft) и ЛП (lpc), одного фрагмента

Поиск трансформированного файла с помощью ЛП

Идея поиска заключается в сравнении спектров,полученных с помощью ЛП, фрагментов оригинального файла и трансформированного файла. В исходном файле выбирается фрагмент FragmOrig с определёнными временными маркерами. Затем в исследуемом файле находится фрагмент FragmC с теми же временными маркерами. После этого сравниваются нормированные спектры этих фрагментов. В качестве меры близости используем скалярное произведение спектров ( в случае совпадения скалярное произведение равно 1). Чтобы понять, как полученные значения отличаются от аналогичных значений, подсчитанных для произвольного фрагмента FragmX , для этого случайного фрагмента производятся аналогичные вычисления. Точный смысл сказанного понятен из следующего кода.

def changeRate(Name,NewBitRate):
    
Song = asgm.from_file(Name+'.wav',format='wav')
Song.export('Temp.mp3', format='mp3',bitrate=NewBitRate)
Song = asgm.from_file('Temp.mp3',format='mp3')
Song.export(Name+'Mod'+'.wav', format='wav')

Fr = 44100 
AllAv = []FragmOrig = Dat[10Fr:11Fr]
AV = getLpcSpec(FragmOrig)
AllAv.append(AV)
FragmX = Dat[20Fr:21Fr]AV = getLpcSpec(FragmX)
AllAv.append(AV)
Fragm3 = FragmOrig[::2]
AV = getLpcSpec(Fragm3)
AllAv.append(AV)
Fragm4 = FragmX[::2]
AV = getLpcSpec(Fragm4)
AllAv.append(AV)
B = sgn.firwin(7,10000, fs = Fr)
Fragm5 = sgn.lfilter(B,[1.,],FragmOrig)
AV = getLpcSpec(Fragm5)
AllAv.append(AV)
Fragm6 = sgn.lfilter(B,[1.,],FragmX)
AV = getLpcSpec(Fragm6)
AllAv.append(AV)
write('FragmOrig.wav',Fr,FragmOrig)
changeRate('FragmOrig','190000')
[Fr,Fragm7] = read('FragmOrigMod.wav')
AV  = getLpcSpec(Fragm7)
AllAv.append(AV)
write('FragmX.wav',Fr,FragmX)
changeRate('FragmX','190000')
[Fr,Fragm8] = read('FragmXMod.wav')
AV  = getLpcSpec(Fragm8)
AllAv.append(AV)
#
for I in range(len(AllAv)):
    print(str(I),np.dot(AllAv[0],AllAv[I]))

Здесь Dat есть результат загрузки файла с песней, функция firwin вычисляет коэффициенты фильтра низких частот, а lfilter осуществляет фильтрацию.

Выводы

Из приведённых вычислений следует устойчивость сглаженного спектра к рассмотренным преобразованиям. Использованная оценка близости двух спектров с помощью скалярного произведения является довольно грубой. Применение кластеризации на основе нейронной сети должно привести к лучшим результатам. Надёжность самого метода повыситься, если использовать несколько оригинальных фрагментов из файла. Все методы указанного типа имеют общий недостаток -- они чувствительны к смещению временных маркеров в результате удаления отдельных участков файла. Для уменьшения этой чувствительности выделяют особые точки с необычным спектром, а временные маркеры привязывают к этим точкам.