Статья посвящена созданию интерактивного тумана в реальном времени в произвольных границах при помощи симуляции жидкости и вычислительных шейдеров Unity 3D. В статье я рассмотрю простой способ генерации маски для произвольных границ и расскажу о двух способах решения проблем, связанных с трёхмерным рельефом. Также я поделюсь мелкими улучшениями, которые можно добавить в систему.

В этом посте я не буду говорить о том, как запрограммировать симуляцию жидкости, потому что подробно рассмотрел эту тему в предыдущем посте Gentle Introduction to Realtime Fluid Simulation for Programmers and Technical Artists [перевод на Хабре].

Как обычно, код выложен на моём Github: https://github.com/IRCSS/Compute-Shaders-Fluid-Dynamic-

Также вы можете скачать/просмотреть использованную в демо модель на моём Sketchfab.

Рендеринг объёмов

Чтобы приступить к созданию тумана, нам первым делом нужно найти способ рендеринга данных объёмов. Существуют различные способы рендеринга тумана, например, ray marching на поверхности четырёхугольника с параллельным поиском карты высот, сгенерированной нашим движком симуляции жидкости. Для своего демо я решил выбрать нечто более простое: наложить друг на друга несколько прозрачных плоскостей, создающих ощущение рендеринга объёма. В качестве маски прозрачности для тумана я использую текстуру краски, сгенерированную движком жидкости.

Я рассказывал об этой технике в одном из моих предыдущих постов про объёмную траву, где объяснил, как генерировать эти плоскости в геометрическом шейдере. Для этого визуального эффекта я хотел генерировать их на стороне CPU. Разумеется, можно создать стандартную плоскость в Unity, одновременно сгенерировать несколько её экземпляров и отобразить её размеры на область, где выполняется симуляция. Однако поскольку я помечаю область симуляции при помощи разметки углов квадрата симуляции четырьмя пустыми игровыми объектами, было решено генерировать меш процедурно. Благодаря этому вершины в буфере вершин точно совпадают с пространством симуляции.

Вот код, генерирующий меш для плоскости, а также UV, соответствующие пространству симуляции в вычислительных шейдерах:

    //    3---------2
    //    | .       |
    //    |   .     |
    //    |     .   |
    //    |       . |
    //    0---------1

    void GeneratePlaneMesh(ref Mesh toPopulate)
    {
        toPopulate.vertices  = new Vector3[] { corners.leftBottom.position, corners.rightBottom.position, corners.rightUp.position, corners.leftUp.position };
        toPopulate.triangles = new int[] { 0, 3, 1,    // First  Triangle
                                           1, 3, 2 };  // Second Triangle
        toPopulate.uv        = new Vector2[] { new Vector2(0.0f, 0.0f), new Vector2(0.0f, 1.0f), new Vector2(1.0f, 1.0f), new Vector2(1.0f, 0.0f) };

    }

Рисунок 1. Код генерации меша одной плоскости

Далее я генерирую нужное количество плоскостей в цикле for, назначаю им материалы и прикрепляю их к игровым объектам. При этом создаются вызовы отрисовки по количеству плоскостей, что неидеально в условиях, когда производительность критически важна. Я поступил так, чтобы оставить сортировку прозрачных слоёв, что важно для правильного смешивания в рендерере Unity. В ситуации (подобной нашей) когда симуляция всегда будет видна сверху, можно предположить, что всегда правильно рендерить слои сверху вниз. Можно поместить все слои в один меш и отсортировать буфер индексов таким образом, чтобы отрисовывать всё за один вызов отрисовки.

        fluid_simulater.UpdateArbitaryBoundaryOffsets(obstcleMap, resources);
        //--------------------------------------------
        // Generate fog Mesh

        Mesh fogMeshBase = new Mesh();
        GeneratePlaneMesh(ref fogMeshBase);

        fogRenderStackMats = new Material[fogStackDepth];

        Shader s = Shader.Find("Unlit/VastlandFog");
        if (!s) { Debug.LogError("Couldnt find the Vastland Fog shader!"); return; }

        for (int i = 0; i < fogStackDepth; i++)
        {
            fogRenderStackMats[i] = new Material(s);
            fogRenderStackMats[i].SetFloat("StackDepth", (float)i / (float)fogStackDepth);

            GameObject gb = new GameObject("FogStack_" + i.ToString());
            MeshRenderer mr = gb.AddComponent<MeshRenderer>();
            mr.sharedMaterial = fogRenderStackMats[i];
            gb.transform.position = new Vector3(0.0f, (float)i * distanceBetwenPlanes, 0.0f);
            gb.AddComponent<MeshFilter>().sharedMesh = fogMeshBase;

            if (i != 0) continue;
            fogCollider = gb;
            fogCollider.AddComponent<MeshCollider>().sharedMesh = fogMeshBase;

        }

Рисунок 2. Создание стопки слоёв

Вот как это выглядит в движке:


Рисунок 3. Визуализация стопки

Создание карты препятствий

Как говорилось в предыдущей статье в разделе «Границы и произвольные границы», нужно передать движку симуляции жидкости некую маску, чтобы он знал, где находятся произвольные границы в пределах области симуляции. В данном случае произвольной границей является любой объект внутри симуляции, блокирующий движение жидкости. Например, горы должны препятствовать движению тумана и отражать его. Если вы хотите узнать, как это реализовано, прочитайте предыдущую статью, и особенно документацию к коду в разделе о границах. Хитрость здесь заключается в том, чтобы генерировать маску автоматически.


Рисунок 4. Сравнение высоты препятствий с высотой области симуляции в пространстве камеры

Проще всего это можно сделать при помощи информации о глубине в сцене; это позволяет узнать, какой объект находится выше плоскости симуляции. Любая область выше плоскости симуляции является препятствием в плоскости. Это допущение верно для нашего случая (не совсем полностью, до достаточно корректно), но может быть неверным в других случаях, которые я рассмотрю ниже. Вот краткое описание того, как получить маску на основании этого способа:

1. Отрендерить глубину сцены (все объекты, которые должны использоваться как препятствия). Камера должна быть перпендикулярна к пространству симуляции и иметь ортогональную проекцию (в нашем случае и в большинстве случаев это будет вид сверху вниз, при котором камера смотрит на симуляцию)
2. Берём текстуру, полученную на этапе 1, и выполняем проверку того, какой пиксель ближе к камере, чем плоскость симуляции (то есть выше, чем плоскость симуляции). Делаем эти пиксели белыми, этот цвет кодирует пиксель, перекрытый препятствиями.
3. После этапа 2 у нас остаётся чёрно-белая маска всех препятствий, которую мы передаём движку жидкости.

Создание карты глубин для препятствий

Для начала нам нужно каким-то образом узнать, какие объекты в сцене будут препятствовать жидкости. Я помечаю их в сцене и скрипт собирает все объекты с этой меткой в один массив. Далее нам нужно отрендерить глубину всех этих объектов в текстуру из вида сверху вниз. Для этого я использую метод Graphics.DrawNow, который мгновенно отрисовывает объекты при его вызове. Это предпочтительно для меня, потому что я вызываю функцию только один раз в начале и хочу, чтобы после завершения функции Start карта была готова для первого кадра рендеринга.

Первым делом нам нужно создать «камеру», рендерящую эти объекты. Я поставил кавычки, потому что на самом деле методу DrawNow не передаётся камера. Камера по сути своей является только абстракцией, в которую включена матрица преобразований, render target и код для усечения, сортировки, параметров рендеринга и т. п. Матрицу преобразований нам нужно создать.

Если вы плохо знаете матрицы, то рекомендую прочитать мою шпаргалку Matrices for Tech Artists. Краткое описание: «камера» — это матрица, получающая 3D-объект, она проецирует его на 2D-поверхность, которая пересекается с изображением (текстурой), создаваемой рендерингом. Матрица, которую нам нужно создать, будет влиять на вершины мешей препятствий, позиции которых выражены в локальном пространстве. Вот этапы, которые необходимы для перехода из локального пространства в пространство усечения:

1. Из модели (локальное пространство) в мировое пространство: local2World Matrix
2. Из мирового пространства в пространство камеры (локальное пространство игрового объекта-камеры): View Matrix
3. Из пространства камеры в пространство усечения: Projection Matrix

Чтобы получить готовую матрицу MVP, которую мы умножаем на o.vertex в вершинном шейдере (частично в Unity этим занимается макрос UnityObjectToClipPos), нужно перемножить всё это:

MVP = Projection* View * local2World

Матрицу local2World можно легко получить из игровых объектов препятствий при помощи gameobject.transform.localToWorld.

Если бы у нас была настоящая камера (которую можно создать и расположить вручную, чтобы избежать всех дальнейших математических вычислений), то мы могли бы получить View, выполнив Camera.transform.localToWorld.Inverse.

Кроме того, если включить для камеры ортогональную проекцию и изменить её размер так, чтобы она идеально накладывалась на область симуляции, то мы могли бы также получить матрицу проекции при помощи Camera.projectionMatrix.

Однако работа вручную более трудоёмка, чем написание функции для создания матрицы, рендерящей нашу область симуляции с попиксельной точностью.

Сначала нам нужно создать матрицу вида. Для этого я выполняю следующие шаги:

1. Беру векторы, представляющие края четырёхугольника симуляции, и при помощи векторного произведения нахожу нормаль к плоскости симуляции.
2. Далее я нахожу среднюю точку области симуляции и прибавляю нормаль, умноженную на смещение до средней точки; таким образом я располагаю камеру где-то над пространством симуляции.
3. В качестве вектора направления камеры (forward vector) мы берём перевёрнутую нормаль к плоскости (-normal), в качестве правого вектора (right vector) — одну из граней четырёхугольника симуляции (предпочтительно расположенную вдоль оси X), а в качестве вектора вверх (up) мы берём векторное произведение между ними двумя.

Мы упаковываем оси forward, right и up, а также позицию камеры в матрицу 4х4, создавая таким образом камеру, смотрящую вниз в пространстве симуляции и расположенную в середине области. При ортогональной проекции неважно, где находится камера вдоль нормали к плоскости симуляции, но для визуальной отладки я всё равно располагаю её на некотором расстоянии. Более подробное объяснение создания матрицы вида на основе векторов forward, right и up см. в моей статье Look At Transformation Matrix in Vertex Shader.

    Matrix4x4 ConstructTopDownOrthoCameraMatrix(SimulationDomainIndicator domainIndicator, Vector3 globalMin, Vector3 globalMax)
    {
        Vector3 halfPoint = domainIndicator.leftBottom.position + (domainIndicator.rightUp.position - domainIndicator.leftBottom.position) * 0.5f; // find mid point (A+B)/2
        Vector3 offset    = Vector3.Cross( (domainIndicator.leftUp.position - domainIndicator.leftBottom.position).normalized, (domainIndicator.rightBottom.position - domainIndicator.leftBottom.position).normalized);

        Vector3 cameraPos = halfPoint + offset * 10.0f;
        Vector3 forward   = -offset;
        Vector3 right     = (domainIndicator.rightBottom.position - domainIndicator.leftBottom.position).normalized;
        Vector3 up        = Vector3.Cross(forward, right);

        
        Matrix4x4 cameraToWorld = new Matrix4x4(forward, up, right, new Vector4(cameraPos.x, cameraPos.y, cameraPos.z, 1.0f));
        Matrix4x4 worldToCamera = cameraToWorld.inverse;

Рисунок 5. Построение матрицы вида

Следующий шаг заключается в построении матрицы проекции. При ортогональной проекции это сделать гораздо проще, чем при перспективной. После того, как модель подверглась преобразованию вида, все координаты выражены в локальном пространстве игрового объекта камеры. После матрицы проекции нам нужно получить компонент xyz в интервале от -1 до 1 и среднюю точку симуляции, находящуюся в (0, 0, 0). Это значит, что четыре угла будут находится в перестановках 1 и -1. Что касается интервала координат Z, мы хотим, чтобы то, что находится на дальней плоскости усечения, было отображено на 1, а то, что находится на ближней, было отображено на -1, и эти значения тоже должны определять мы. Чтобы вычислить это, я обхожу в цикле все препятствия, нахожу минимум и максимум их ограничивающего прямоугольника и задаю минимум и максимум в пространстве камеры в качестве ближней и дальней плоскостей усечения.

В показанном ниже коде (Рисунок 6) вы видите описанный выше процесс. Мы масштабируем xy так, чтобы четыре угла плоскости симуляции были отображены на интервал от -1 до 1, а z было таким, что высочайший горный пик имел координату -1, а самое нижнее основание меша имело координату 1. Также я вычитаю среднюю точку, чтобы средняя точка перенеслась в точку начала координат (0, 0, 0).

Последняя деталь — это маленькая матрица перестановок, которую я использую, потому что создаю свою матрицу вида с осью x в качестве forward, y — в качестве up и z — в качестве right, а Unity использует x — right, y — up и z — forward. Также здесь я меняю местами ось вверх и вправо, чтобы сопоставить поворот камеры и само пространство симуляции в вычислительных шейдерах.

        float scale_xy = (domainIndicator.rightBottom.position - domainIndicator.leftBottom.position).magnitude *0.5f;
        

        Vector3 minCamSpace = worldToCamera * new Vector4(globalMin.x, globalMin.y, globalMin.z, 1.0f);
        Vector3 maxCamSpace = worldToCamera * new Vector4(globalMax.x, globalMax.y, globalMax.z, 1.0f);
        
        float midPoinZ = Mathf.Abs(maxCamSpace.x + minCamSpace.x) * 0.5f;          // after the transformation the mesh is always on the positive side, since the camera is placed that way, however it can be that the min and max switch places, if the camera is rotated 
        float scaleZ   = Mathf.Abs(maxCamSpace.x - minCamSpace.x) * 0.5f;



        Matrix4x4 permutationMatrix = new Matrix4x4(new Vector4(    0.0f,    0.0f,    1.0f, 0.0f),
                                                    new Vector4(    1.0f,    0.0f,    0.0f, 0.0f),
                                                    new Vector4(    0.0f,    1.0f,    0.0f, 0.0f),
                                                    new Vector4(    0.0f,    0.0f,    0.0f, 1.0f)); 



        Matrix4x4 orthoProjection = new Matrix4x4(new Vector4(1.0f / scale_xy,            0.0f,          0.0f, 0.0f),
                                                  new Vector4(           0.0f, 1.0f / scale_xy,          0.0f, 0.0f),
                                                  new Vector4(           0.0f,            0.0f,  1.0f/ scaleZ, 0.0f),
                                                  new Vector4(           0.0f,            0.0f, -midPoinZ/ scaleZ, 1.0f));
        
        return orthoProjection * permutationMatrix * worldToCamera;
    }

Рисунок 6. Создаём матрицу проекции

После этого всё остальное будет просто: обходим в цикле все препятствия, создаём матрицу MVP и записываем их глубины в render target. Небольшая деталь: в шейдере я отображаю значения глубин из интервала от -1 до 1 на интервал от 0 до 1, потому что Unity ожидает их в таком формате.

         worldToSimulationCameraMatrix = ConstructTopDownOrthoCameraMatrix(corners, globalMin, globalMax);
        

        Material constructObstcleDepth = new Material(Shader.Find("Unlit/ObstclesDepthMap"));
        Material constructObstcleMask = new Material(Shader.Find("Unlit/ConstructObstcleMap"));

        Graphics.SetRenderTarget(target);

        constructObstcleDepth.SetPass(0);
        foreach (GameObject gb in toRender)
        {
            MeshFilter mf = gb.GetComponent<MeshFilter>();
            Mesh meshToRender = mf.sharedMesh;

            Matrix4x4 MVP = worldToSimulationCameraMatrix * gb.transform.localToWorldMatrix;
        
            Shader.SetGlobalMatrix("Obstcle_MVP", MVP);


            Graphics.DrawMeshNow(meshToRender, Matrix4x4.identity, 0);
        }
        Graphics.SetRenderTarget(null);

        RenderTexture temp = RenderTexture.GetTemporary( target.width, target.height);
        temp.Create();

        Vector3 halfPoint = corners.leftBottom.position + (corners.rightUp.position - corners.leftBottom.position) * 0.5f; // find mid point (A+B)/2
        halfPoint = worldToSimulationCameraMatrix * new Vector4(halfPoint.x, halfPoint.y, halfPoint.z, 1.0f);

        Graphics.Blit(target, temp);

        constructObstcleMask.SetTexture("_ObstcleDepthMap", temp);
        constructObstcleMask.SetFloat  ("_simulationDepth", halfPoint.z);
        Graphics.Blit(temp, target, constructObstcleMask);

Рисунок 7. Глубины рендеринга препятствий

Ваша карта глубин должна выглядеть примерно так:


Рисунок 8. Карта глубин

Создание маски препятствий из карты глубин

Это будет очень короткий этап. Получив карту глубин, мы вычисляем глубину плоскости в пространстве проекции и за один проход после прохода глубин определяем, выше или ниже пространства симуляции находится пиксель.

            fixed4 frag (v2f i) : SV_Target
            {
                float2 uv = i.uv.xy;  
                uv.y = 1. - uv.y;     // mapping from the texture to the compute shader space  

                float c = tex2D(_ObstcleDepthMap, uv).x;
                c = c <= _simulationDepth + 0.025? 1.0 : 0.;
                
                return float4(c.xxx, 1.);
            }
            ENDCG

Рисунок 9. Построение маски из маски глубин

Ваша маска должна выглядеть так, её можно передать движку симуляции:


Рисунок 10. Маска препятствий

Проблема с нависающими элементами в рельефе

В такой системе есть проблема. Посмотрите на рисунок 11:


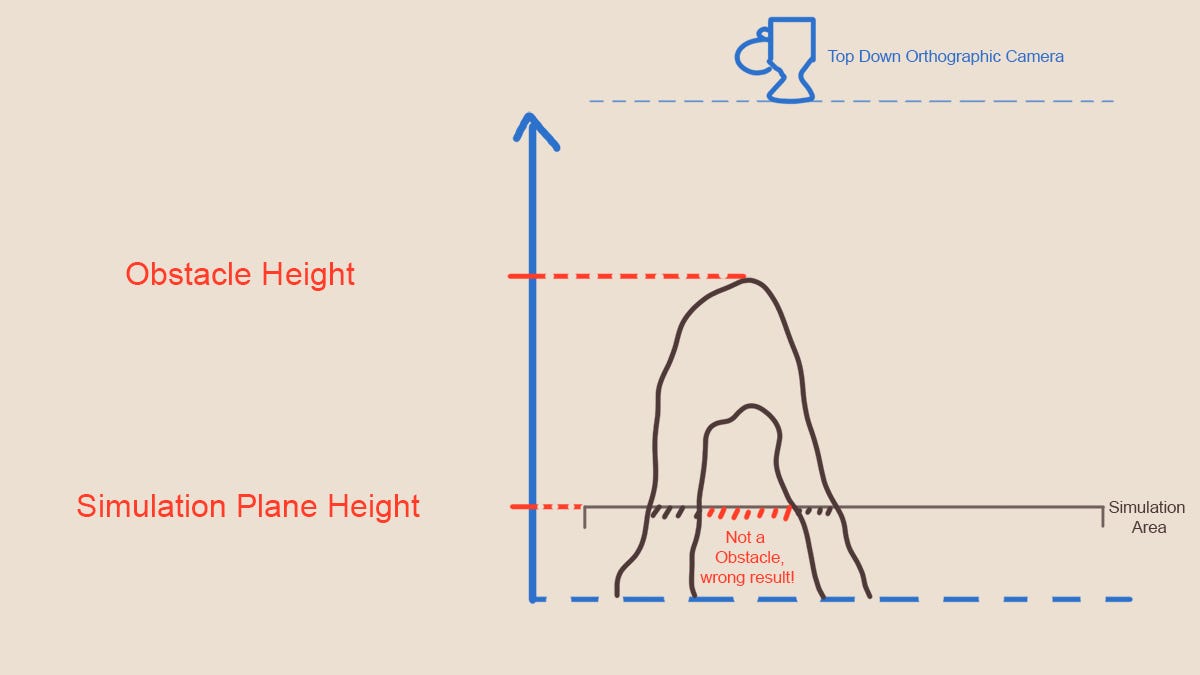
Рисунок 11. Рельеф с нависающим элементом

Наш алгоритм ошибочно пометит красную область как заблокированную; причина заключается в нависании, которое перекрывает обзор камере на пространство между нависающей частью и пространством симуляции. Такие структуры встречаются довольно часто, однако в рельефе их обычно избегают, потому что он создаётся на основе карт высот, а карты высот могут расширяться только вверх и не образуют нависаний. Мой рельеф искажён в плоскости XZ, поэтому у меня есть небольшие нависания, но их недостаточно, чтобы оправдать реализацию более сложного алгоритма. Тем не менее, я немного поразмыслил над этой проблемой, и у меня возникли мысли о том, как её решить.

Описание в виде SDF

Вероятно, первое, что приходит в голову большинству разработчиков. Если представить плоскость симуляции в виде знакового поля с расстояниями относительно препятствий, то можно легко определить, находится ли что-то внутри или снаружи препятствий. Для каждого пикселя карты оно указывает в направлении ближайшего к этому пикселя препятствия в пространстве симуляции. Реализация такой схемы немного трудоёмка, поэтому это не было бы моим первым выбором, если бы я хотел создать её только для карты с произвольными границами. Но если у нас есть эта информация, можно создать карту потоков (векторное произведение вектора sdf и нормалью к плоскости симуляции; само по себе знаковое поле расстояний является полем скаляров, но вместо них можно сохранить в компоненте w вектор с внутренней и наружной стороной). Если применить оператор Projection, о котором я говорил в прошлой статье, то мы получим карту потоков без дивергенции, которую можно использовать для перемещения объектов, панорамного шума и т. д. Можно даже получить достаточно правдоподобное «фальшивое» поведение жидкости без необходимости симуляции.

Метод Count Up Count Down

Второй метод, который пришёл мне в голову, в качестве источника вдохновения использует технику теневых объёмов, применённую в старых играх наподобие Doom 3. Сложность здесь заключается в поиске способа определения, находится ли пиксель внутри объёма, что очень похоже на нашу ситуацию. Не знаю, какое подходящее название можно придумать для этой техники, но принцип «count up and count down» («счёт вверх, счёт вниз») объясняет её лучше всего.

Мы по-прежнему рендерим сцену сверху вниз, а объекты помечаются как потенциальные препятствия. Однако на этот раз мы не используем Z-тест и усечение. Это значит, что все грани будут отрендерены вне зависимости от того, направлены ли они в камеру, или нет. Каждый раз, когда мы встречаем пиксель, направленный в камеру, инкрементируем значение этого пикселя в буфере, а каждый раз, когда находим пиксель, направленный от камеры, выполняем декремент значения. Объяснение см. на рисунке 12.


Рисунок 12. Техника Count Up and Down

Для центральной области у нас правильно получится 0, то есть эта область не внутри препятствия, следовательно, область рядом с ней из-за отсутствия декремента получит 1, и эта область корректно будет помечена как граница.

Возможно, это можно реализовать в альфа-смешении или использовать стенсил наподобие теневого объёма. Вероятно, проще всего будет привязать к пиксельному шейдеру буфер Structured с правом доступа для произвольной записи, и использовать его для сохранения значения того, сколько смотрящих вверх и вниз граней было посещено в этом фрагменте.

Стоит упомянуть, что эта техника не будет работать в топологии многообразия. Но эта проблема присуща и методу с SDF, поскольку не существует хороших способов извлечения описания объёма меша с рёбрами многообразия.

В заключение

Если вы захотите усовершенствовать эту систему, то больше всего можно выиграть от добавления к туману макродеталей на основе шума. Как сказано в посте про симуляцию жидкости, ваша симуляция может иметь ограниченное разрешение, а мелкие движения можно имитировать при помощи шума.

Мелкие движения не обязаны быть очень точными, и существует множество техник, позволяющих увеличить визуальную чёткость тумана. Я подробно описывал их в статье VR performance challenges and creating realistic fog in Unity. В ней я также упомянул размытие экрана перед туманом для добавления реализма; это не подходит для нашего демо, но возможность такого улучшения определённо стоит рассмотреть. Результат применения этих техник можно посмотреть в видео:


Кроме того, как и в моей демо-сцене с персидским садом, вы можете использовать буфер давлений, чтобы настраивать толщину объёмного тумана. Это добавит туману больше вариативности по направленной вверх оси и он будет выглядеть более трёхмерным.