Всем привет! На связи команда ad-hoc аналитики X5 Tech.
Сегодня подробно обсудим применение стратификации для повышения чувствительности оценки AB экспериментов.
Вы узнаете:
что такое стратифицированное семплирование;
два способа точечной оценки выборочного среднего;
в чём отличие стратификации и постстратификации;
как стратификация влияет на дисперсию метрики.
Прежде чем мы начнём - пару слов о нас. Мы работаем в Департаменте аналитики данных, который находится в Х5 Tech. X5 Tech - это бизнес-единица Х5 Group, которая отвечает за цифровые решения. У нас работает около 200 человек, среди которых 70 дата сайентистов и 50 дата аналитиков. Большая часть сотрудников распределена по продуктовым командам, которые занимаются прогнозированием спроса, оптимизацией ассортимента, проведением промо-кампаний и многим другим.
Помимо продуктовых команд, есть отдельная команда Ad-hoc аналитики.
Задачи Ad-hoc команды:
помогаем бизнес-подразделениям с запросами по анализу данных, которые не вписываются в существующие продукты;
помогаем продуктовым командам, если им нужны дополнительные руки;
занимаемся A/B-тестированием – и это основная функция команды.
Пример AB эксперимента
Начнём с рассмотрения примера. Допустим, у нас есть интернет-магазин продуктов с доставкой, и мы хотим стимулировать увеличение средней выручки на пользователя. Для этого мы решили отправить письма с рекламой сервиса активным клиентам. Перед тем как запустить рассылку на всех активных клиентов, нужно проверить её эффективность с помощью AB эксперимента.
В самом простом сценарии для этого потребуется:
Определить целевую метрику.
Сформулировать статистическую гипотезу и критерий её проверки.
Зафиксировать минимальный ожидаемый эффект и допустимые вероятности ошибок I и II рода.
Оценить необходимый размер групп.
Сформировать экспериментальную и контрольную группу.
Провести эксперимент.
Оценить результаты эксперимента.
Рассмотрим каждый из пунктов чуть подробнее.
1. Определить целевую метрику
Целевая метрика должна хорошо отражать конечную цель изменений, по ней будем оценивать успешность эксперимента. В нашем случае в качестве целевой метрики возьмём среднюю выручку на клиента за время эксперимента.
2. Сформулировать статистическую гипотезу и критерий её проверки
Будем проверять гипотезу о равенстве средних. Нулевая гипотеза - средние равны, альтернативная - средние не равны. В качестве критерия возьмём тест Стьюдента. Время эксперимента положим равным одной неделе.
3. Зафиксировать минимальный ожидаемый эффект и допустимые вероятности ошибок I и II рода
Эти параметры нужны для оценки необходимого размера групп.
Напомним, что ошибка первого рода - это событие, заключающееся в том, что мы говорим, что эффект есть, когда его нет. Ошибка второго рода - событие, заключающееся в том, что мы говорим, что эффекта нет, когда на самом деле он есть.
Легко показать, что если мы хотим быть способны обнаружить сколь угодно малый эффект, или никогда не ошибаться, то потребуется бесконечное количество наблюдений. Бесконечного количества пользователей для проведения эксперимента у нас нет. Возьмём более приземлённые значения. Вероятности ошибок I и II рода положим равными 0.05 и 0.20 соответственно. Допустим, для пользователей, попадающих под условия эксперимента, на исторических данных мы получили оценку средней выручки (2500 рублей) и оценку её стандартного отклонения (800 рублей). После рассылки писем будем ожидать, что выручка увеличится минимум на 100 рублей.
4. Оценить необходимый размер групп
Это можно сделать по формуле

где - вероятность ошибки I рода,
- вероятность ошибки II рода, σ² - дисперсии значений в контрольной и экспериментальной группах, ε - минимальный ожидаемый эффект.
Вычислим размер выборки:
import numpy as np
from scipy import stats
alpha = 0.05 # вероятность ошибки I рода
beta = 0.2 # вероятность ошибки II рода
mu_control = 2500 # средняя выручка с пользователя в контрольной группе
effect = 100 # размер эффекта
mu_pilot = mu_control + effect # средняя выручка с пользователя в экспериментальной группе
std = 800 # стандартное отклонение
t_alpha = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
t_beta = stats.norm.ppf(1 - beta, loc=0, scale=1)
var = 2 * std ** 2
sample_size = int((t_alpha + t_beta) ** 2 * var / (effect ** 2))
print(f'sample_size = {sample_size}')sample_size = 1004Получилось sample_size = 1004.
Проверим, что при таком размере групп вероятности ошибок контролируются на заданных уровнях. Это можно сделать с помощью синтетических AA и AB тестов. Будем генерировать пары выборок с эффектом и без эффекта и считать доли случаев, когда тест Стьюдента ошибся.
В данном примере для простоты генерируем данные из нормального распределения. На практике следует семплировать данные из эмпирического распределения, построенного на реальных исторических данных.
first_type_errors = []
second_type_errors = []
sample_size = 1004
for _ in range(10000):
control_one = np.random.normal(mu_control, std, sample_size)
control_two = np.random.normal(mu_control, std, sample_size)
pilot = np.random.normal(mu_pilot, std, sample_size)
_, pvalue_aa = stats.ttest_ind(control_one, control_two)
first_type_errors.append(pvalue_aa < alpha)
_, pvalue_ab = stats.ttest_ind(control_one, pilot)
second_type_errors.append(pvalue_ab >= alpha)
part_first_type_errors = np.mean(first_type_errors)
part_second_type_errors = np.mean(second_type_errors)
print(f'part_first_type_errors = {part_first_type_errors:0.3f}')
print(f'part_second_type_errors = {part_second_type_errors:0.3f}')part_first_type_errors = 0.052
part_second_type_errors = 0.200Получили значения близкие к 0.05 и 0.2, как и должно было быть. Значения могут немного меняться от запуска к запуску из-за случайности генерируемых данных.
На практике точные значения параметров распределений неизвестны, вместо точных значений используются их оценки. Оценки параметров могут несколько отличаться от истинных значений, поэтому полученная оценка размера выборки не является абсолютно точной. Чтобы тест наверняка контролировал вероятности ошибок на заданном уровне, мы рекомендуем брать размер групп чуть больше рассчитанного значения.
Пусть размер групп будет равен 1100. Если запустить тот же скрипт с sample_size=1100, то оценка вероятности ошибки первого рода останется равной примерно 0.05, а второго рода уменьшится.
5. Сформировать экспериментальную и контрольную группы
Мы определились с размером групп, теперь нужно выбрать конкретных пользователей для эксперимента. Это можно сделать случайным образом. Такой подход к формированию групп называется случайным семплированием.
Пусть у нас всего 10 тысяч пользователей, тогда выбрать людей для эксперимента можно следующим кодом
user_ids = np.arange(10000)
control_user_ids, pilot_user_ids = np.random.choice(
user_ids, (2, sample_size), replace=False
)6. Провести эксперимент
Отправляем письма пользователям экспериментальной группы и ничего не отправляем пользователям контрольной группы. Ждём неделю.
7. Оценить результаты эксперимента
Когда эксперимент закончен нужно собрать данные для расчёта метрик и провести проверку значимости отличий между группами по алгоритму, который мы зафиксировали до начала эксперимента.
Стратифицированное семплирование
Кажется, мы всё продумали, и можно запускать эксперимент. Но давайте подумаем, возможно, у нас есть дополнительная информация, которая может сделать наш тест лучше.
У нас есть программа лояльности, в которой зарегистрированы не все пользователи нашего магазина. Поведение зарегистрированных пользователей может отличаться от поведения незарегистрированных. Информацию о регистрации в программе лояльности можно использовать для повышения чувствительности эксперимента.
Введём несколько определений:
Ковариата - метрика, которая коррелирует с целевой метрикой, может быть измерена до эксперимента (строго говоря, нет) и не зависит от других экспериментов. В нашем случае факт регистрации в программе лояльности до эксперимента будет ковариатой.
Приведём несколько примеров ковариат для экспериментов с людьми: пол, возраст, город проживания, операционная система устройства пользователя. Если эксперимент проводится не на людях, а на магазинах, то ковариатами могут быть размер торговой площади, расположение (в торговом центре или в отдельном здании), режим работы (круглосуточный или нет) и так далее.
Популяция - все пользователи, на которых мы можем повлиять нашим экспериментом. Пусть в нашей популяции будет 10 тысяч активных пользователей.
С помощью ковариат можно разделить популяцию на непересекающиеся подмножества, которые будут обладать уникальным набором значений ковариат. Такие подмножества будем называть стратами.
В нашем примере будет две страты:
первая - кто не зарегистрирован в программе лояльности;
вторая - кто зарегистрирован в программе лояльности.
Посмотрим на исторические данные пользователей этих страт по отдельности. Допустим, мы выяснили, следующую информацию:
доли страт в популяции равны и составляют 50%;
средняя выручка за неделю в первой страте равна 2000 рублей, во второй - 3000 рублей;
стандартные отклонения выручки за неделю равны 625 рублей в обеих стратах. При таких значениях отклонений объединение данных обеих страт будет иметь отклонение около 800 рублей, как было изначально.
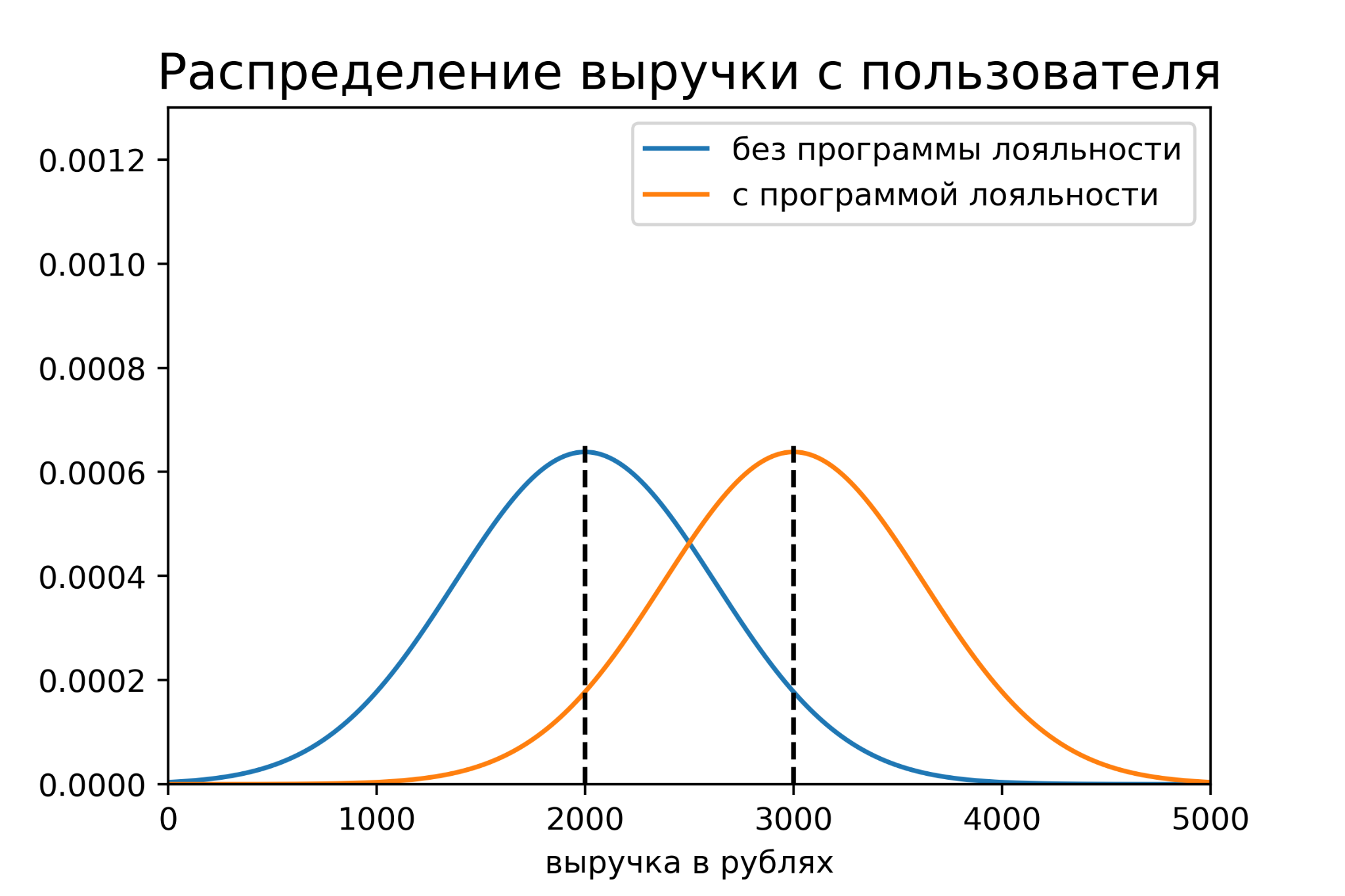
Получается, пользователи разных страт имеют разные распределения метрики.
При случайном распределении пользователей по группам размеры страт могут оказаться неравным: количество пользователей первой страты в контрольной группе может оказаться больше чем в экспериментальной, и наоборот. Это может привести к неверным результатам при оценке пилота, так как средние значения метрики в стратах отличаются.
Было бы хорошо использовать знание о том, что разные группы пользователей ведут себя по-разному во время эксперимента, чтобы убрать факторы, которые могут увеличить вероятность ошибки. Как это сделать?
Есть простое решение. Можно составить контрольную и пилотную группы таким образом, что доли каждой страты будут равны долям страт в популяции.
Технически это сделать довольно просто. Сначала определим, какое количество представителей страт нам нужно в каждой группе, для этого перемножим размер групп с долями страт в генеральной совокупности. В нашем случае получаем для обеих страт 1100*0.5=550. Определив размеры страт в группе, случайным образом выберем соответствующее количество объектов из каждой страты для групп.
Проведём синтетические AA и AB эксперименты для случайного и стратифицированного семплирования, посмотрим как будут отличаться вероятности ошибок.
Для этого нам понадобятся функции генерации данных с помощью случайного и стратифицированного семплирования, а также функция для вычисления pvalue с помощью теста Стьюдента.
Код
import pandas as pd
def get_stratified_data(strat_to_param, effect=0):
"""Генерирует данные стратифицированным семплированием.
Возвращает датафрейм со значениями метрики и страт пользователей
в контрольной и экспериментальной группах.
strat_to_param - словарь с параметрами страт
effect - размер эффекта
"""
control, pilot = [], []
for strat, (n, mu, std) in strat_to_param.items():
control += [
(x, strat,) for x in np.random.normal(mu, std, n)
]
pilot += [
(x, strat,) for x in np.random.normal(mu + effect, std, n)
]
columns = ['value', 'strat']
control_df = pd.DataFrame(control, columns=columns)
pilot_df = pd.DataFrame(pilot, columns=columns)
return control_df, pilot_df
def get_random_data(strats, sample_size, strat_to_param, effect=0):
"""Генерирует данные случайным семплированием.
Возвращает датафрейм со значениями метрики и страт пользователей
в контрольной и экспериментальной группах.
strats - cписок страт в популяции
sample_size - размеры групп
strat_to_param - словарь с параметрами страт
effect - размер эффекта
"""
control_strats, pilot_strats = np.random.choice(
strats, (2, sample_size), False
)
control, pilot = [], []
for strat, (n, mu, std) in strat_to_param.items():
n_control_ = np.sum(control_strats == strat)
control += [
(x, strat,) for x in np.random.normal(mu, std, n_control_)
]
n_pilot_ = np.sum(pilot_strats == strat)
pilot += [
(x, strat,) for x in np.random.normal(mu + effect, std, n_pilot_)
]
columns = ['value', 'strat']
control_df = pd.DataFrame(control, columns=columns)
pilot_df = pd.DataFrame(pilot, columns=columns)
return control_df, pilot_df
def ttest(a: pd.DataFrame, b: pd.DataFrame) -> float:
"""Возвращает pvalue теста Стьюдента.
a, b - данные пользователей контрольной и экспериментальной групп
"""
_, pvalue = stats.ttest_ind(a['value'].values, b['value'].values)
return pvalueСначала запустим АА эксперименты и сравним вероятности ошибок первого рода.
Код
alpha = 0.05 # уровень значимости
N = 10000 # количество пользователей в популяции
w_one, w_two = 0.5, 0.5 # доли страт в популяции
N_one = int(N * w_one) # количество пользователей первой страты
N_two = int(N * w_two) # количество пользователей второй страты
mu_one, mu_two = 2000, 3000 # средние выручки в стратах
std_one, std_two = 625, 625 # стандартное отклонение в стратах
# список страт в популяции
strats = [1 for _ in range(N_one)] + [2 for _ in range(N_two)]
# размер групп эксперимента
sample_size = 1100
sample_size_one = int(sample_size * w_one)
sample_size_two = int(sample_size * w_two)
# маппинг параметров страт
strat_to_param = {
1: (sample_size_one, mu_one, std_one,),
2: (sample_size_two, mu_two, std_two,)
}
random_first_type_errors = []
stratified_first_type_errors = []
random_deltas = []
stratified_deltas = []
for _ in range(10000):
control_random, pilot_random = get_random_data(
strats, sample_size, strat_to_param
)
control_stratified, pilot_stratified = get_stratified_data(
strat_to_param
)
random_deltas.append(
pilot_random['value'].mean() - control_random['value'].mean()
)
stratified_deltas.append(
pilot_stratified['value'].mean() - control_stratified['value'].mean()
)
pvalue_random = ttest(control_random, pilot_random)
random_first_type_errors.append(pvalue_random < alpha)
pvalue_stratified = ttest(control_stratified, pilot_stratified)
stratified_first_type_errors.append(pvalue_stratified < alpha)
part_random_first_type_errors = np.mean(random_first_type_errors)
part_stratified_first_type_errors = np.mean(stratified_first_type_errors)
print(f'part_random_first_type_errors = {part_random_first_type_errors:0.3f}')
print(f'part_stratified_first_type_errors = {part_stratified_first_type_errors:0.3f}')part_random_first_type_errors = 0.048
part_stratified_first_type_errors = 0.013Получилось, что при случайном семплировании оценка вероятности ошибки первого рода равна 0.048, а при стратифицированном - 0.010.
Стратифицированное семплирование снизило вероятность ошибки первого рода более чем в 4 раза!
С одной стороны, уменьшить вероятность ошибки первого рода - это хорошо, так как позволит чаще принимать верные решения. С другой стороны, сильное отличие вероятности ошибки первого рода от заданного уровня значимости - это плохо, так как это не тот тест, который мы хотели построить.
Во время экспериментов мы также сохраняли разницы средних значений выручки между группами, посмотрим как выглядит их распределение.
import seaborn as sns
sns.displot(
{'random_deltas': random_deltas, 'stratified_deltas': stratified_deltas},
kind='kde'
)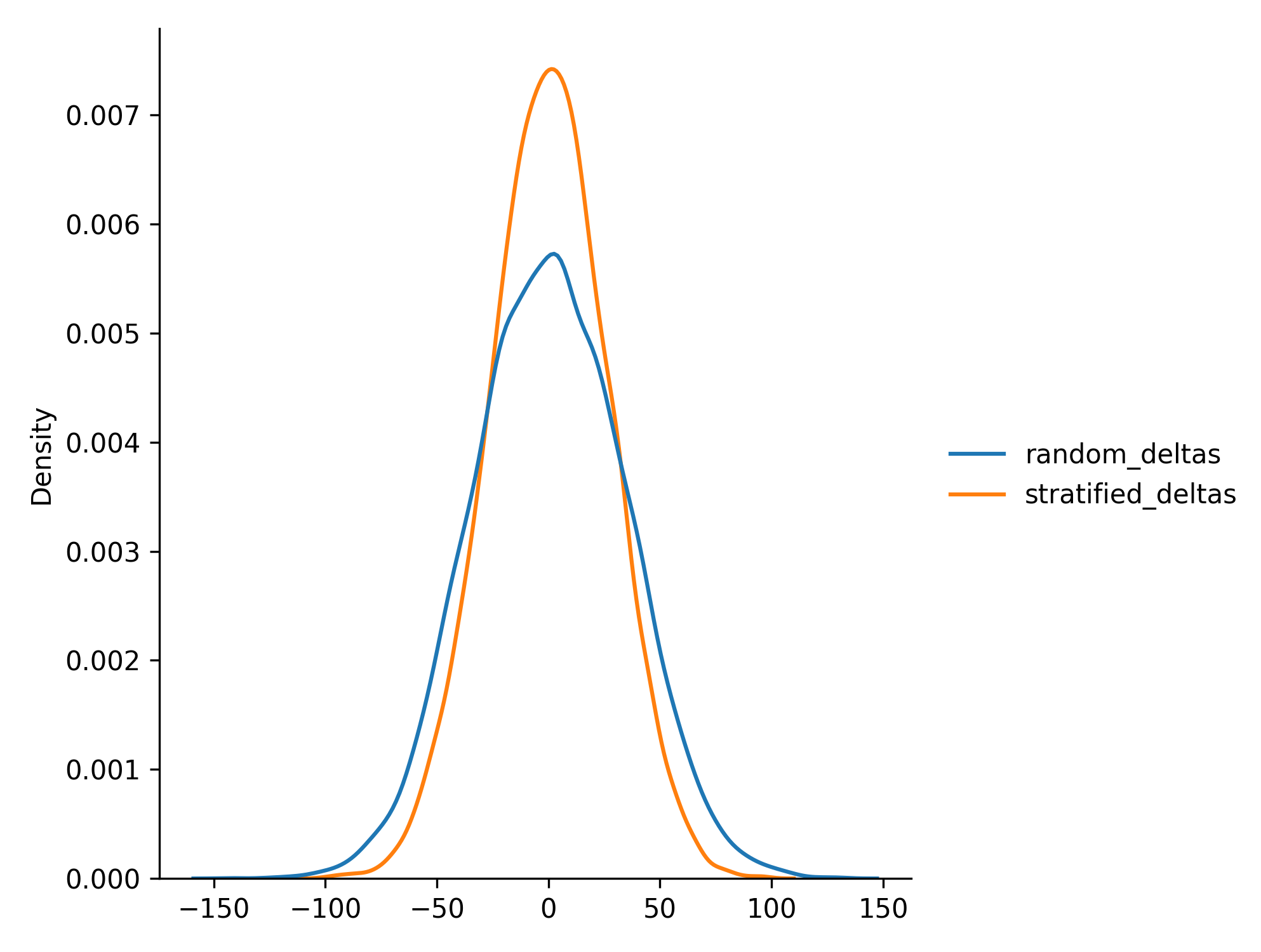
Распределение разницы средних при стратифицированном семплировании имеет менее тяжёлые хвосты и соответственно меньшую дисперсию, что и приводит к уменьшению количества ошибок первого рода.
Оценим вероятности ошибок второго рода, искусственно добавив эффект к экспериментальной группе.
Код
effect = 100
random_second_type_errors = []
stratified_second_type_errors = []
for _ in range(10000):
control_random, pilot_random = get_random_data(
strats, sample_size, strat_to_param, effect
)
control_stratified, pilot_stratified = get_stratified_data(
strat_to_param, effect
)
pvalue_random = ttest(control_random, pilot_random)
random_second_type_errors.append(pvalue_random >= alpha)
pvalue_stratified = ttest(control_stratified, pilot_stratified)
stratified_second_type_errors.append(pvalue_stratified >= alpha)
part_random_second_type_errors = np.mean(random_second_type_errors)
part_stratified_second_type_errors = np.mean(stratified_second_type_errors)
print(f'part_random_second_type_errors = {part_random_second_type_errors:0.3f}')
print(f'part_stratified_second_type_errors = {part_stratified_second_type_errors:0.3f}')part_random_second_type_errors = 0.167
part_stratified_second_type_errors = 0.109Получилось, что при случайном семплировании доля ошибок второго рода равна 0.167, а при стратифицированном - 0.109.
Стратифицированное семплирование уменьшило долю ошибок второго рода примерно в полтора раза!
Стратифицированное семплирование позволило уменьшить вероятности ошибок I и II рода, это очень хорошо. Но мы получили не совсем тот тест, который хотели изначально. Мы хотели проверять гипотезы на уровне значимости 0.05, а получается что проверяем на более низком уровне значимости. Так происходит из-за того, что при стратифицированном семплировании мы не только делаем распределение средних более узким, но и снижаем дисперсию, зафиксировав количество страт в каждой группе. Тест Стьюдента не знает о том, что мы семплируем данные не случайно, поэтому при подсчёте статистики используется завышенная оценка дисперсии. Вернуть тест на нужный уровень значимости нам поможет стратифицированное среднее.
Стратифицированное среднее
При вычислении обычного среднего мы делим суммарную выручку на общее количество пользователей. При вычислении стратифицированного среднего мы считаем обычное среднее для каждой страты по отдельности, а затем вычисляем их взвешенную сумму, где вес страты - доля страты в популяции.
Введём некоторые обозначения:

Тогда простое и стратифицированное среднее можно записать так:

Обратим внимание на два свойства стратифицированного среднего.
Во-первых, при стратифицированном семплировании оценка стратифицированного среднего равна оценке обычного (выборочного) среднего.
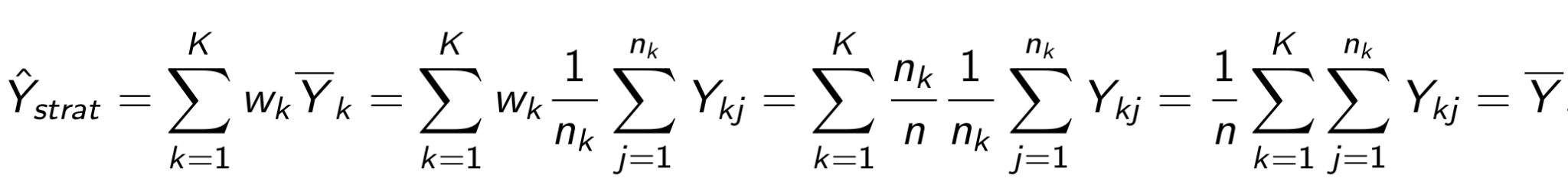
Во-вторых, при случайном семплировании математическое ожидание оценки стратифицированного среднего равно математическому ожиданию оценки обычного среднего. Более того, эти оценки являются несмещенными.

Вычислить оценку дисперсии оценки стратифицированного среднего можно по формуле:
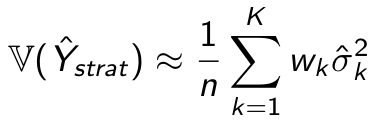
где - оценка дисперсии метрики в соответствующей страте.
Используем эту оценку дисперсии для вычисления статистики нашего теста:
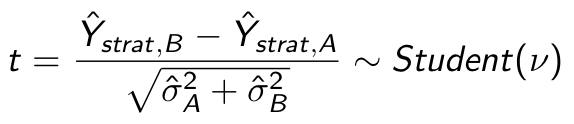
Повторим синтетические АА и АВ эксперименты, используя в качестве метрики стратифицированное среднее.
Код
def calc_strat_mean(df: pd.DataFrame, weights: pd.Series) -> float:
"""Считает стратифицированное среднее.
df - датафрейм с целевой метрикой и данными для стратификации
weights - маппинг {название страты: вес страты в популяции}
"""
strat_mean = df.groupby('strat')['value'].mean()
return (strat_mean * weights).sum()
def calc_strat_var(df: pd.DataFrame, weights: pd.Series) -> float:
"""Считает стратифицированную дисперсию.
df - датафрейм с целевой метрикой и данными для стратификации
weights - маппинг {название страты: вес страты в популяции}
"""
strat_var = df.groupby('strat')['value'].var()
return (strat_var * weights).sum()
def ttest_strat(a: pd.DataFrame, b: pd.DataFrame, weights: pd.Series) -> float:
"""Возвращает pvalue теста Стьюдента для стратифицированного среднего.
a, b - данные пользователей контрольной и экспериментальной групп
weights - маппинг {название страты: вес страты в популяции}
"""
a_strat_mean = calc_strat_mean(a, weights)
b_strat_mean = calc_strat_mean(b, weights)
a_strat_var = calc_strat_var(a, weights)
b_strat_var = calc_strat_var(b, weights)
delta = b_strat_mean - a_strat_mean
std = (a_strat_var / len(a) + b_strat_var / len(b)) ** 0.5
t = delta / std
pvalue = 2 * (1 - stats.norm.cdf(np.abs(t)))
return pvalue
weights = pd.Series({1: w_one, 2: w_two})
first_type_errors = []
second_type_errors = []
for _ in range(10000):
control_aa, pilot_aa = get_stratified_data(
strat_to_param
)
control_ab, pilot_ab = get_stratified_data(
strat_to_param, effect
)
pvalue_aa = ttest_strat(control_aa, pilot_aa, weights)
first_type_errors.append(pvalue_aa < alpha)
pvalue_ab = ttest_strat(control_ab, pilot_ab, weights)
second_type_errors.append(pvalue_ab >= alpha)
part_first_type_errors = np.mean(first_type_errors)
part_second_type_errors = np.mean(second_type_errors)
print(f'part_first_type_errors = {part_first_type_errors:0.3f}')
print(f'part_second_type_errors = {part_second_type_errors:0.3f}')part_first_type_errors = 0.050
part_second_type_errors = 0.035Получаем долю ошибок I рода 0.05 и ошибок II рода 0.035. Теперь тест контролируют вероятность ошибки первого рода на заданном уровне значимости, но при этом его мощность значительно увеличилась.
Стратификация и постстратификация
Таким образом, можно выделить несколько способов:
составления групп:
a. случайное;
b. стратифицированное.оценки среднего:
a. выборочное среднее;
b. стратифицированное среднее.
Более того, их можно комбинировать в различных сценариях.
В базовом варианте мы случайно распределяем пользователей по группам и считаем выборочное среднее. Этот подход может быть не оптимален в случае, если у нас есть дополнительная информация о выборках.
Под стратификацией обычно подразумевают одновременное применение и стратифицированного семплирования для формирования групп, и стратифицированного среднего для оценки среднего выборок. То есть в последнем численном эксперименте мы воспользовались стратификацией. Бывают ситуации, когда нет возможности провести стратифицированное семплирование, но оказывается, что в этом случае все еще можно использовать стратифицированное среднее для получения оценки. Такой подход называют постстратификацией.
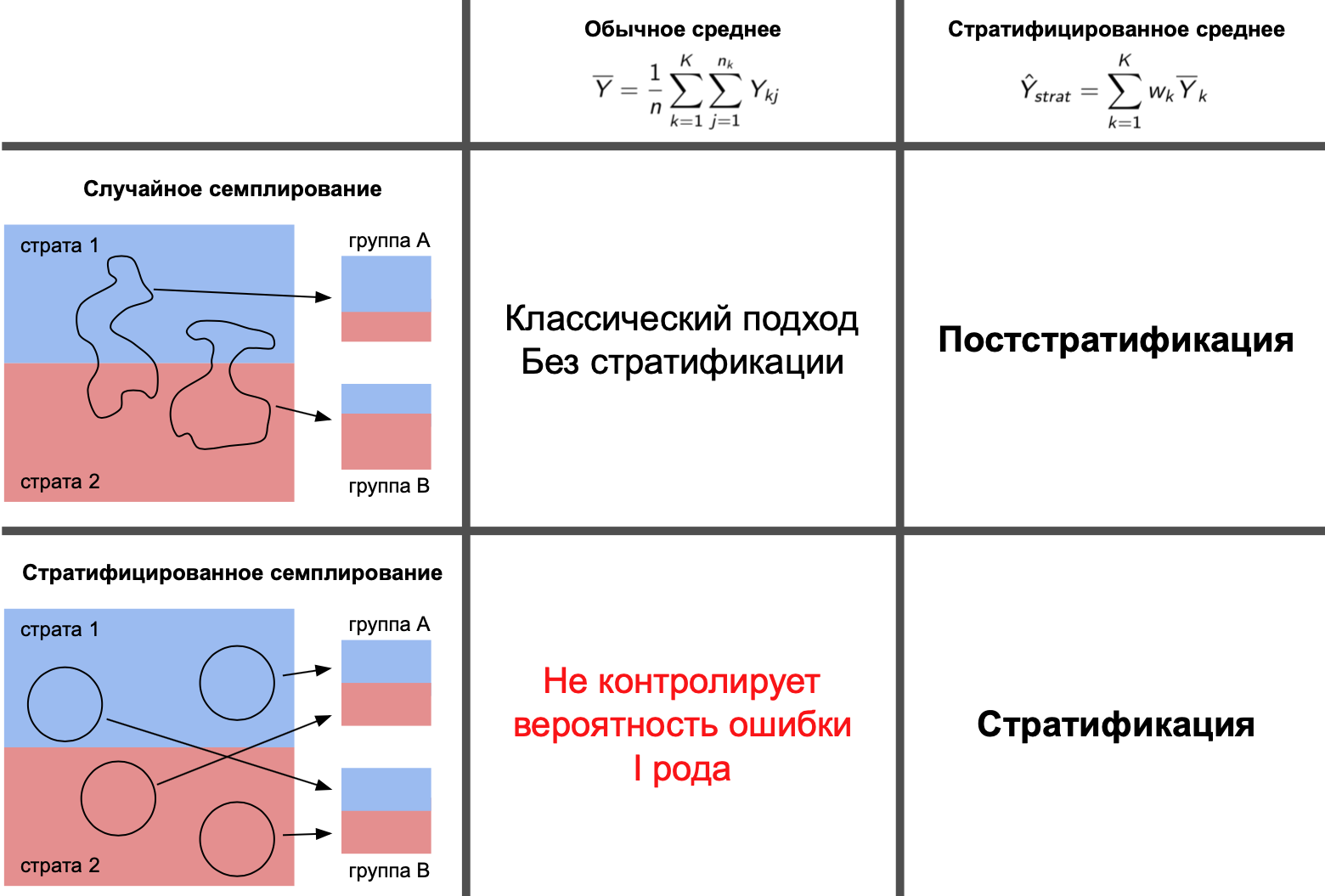
Проверим, что постстратификация тоже увеличивает чувствительность теста. Повторим последний эксперимент, заменив стратифицированное семплирование на случайное семплирование.
Код
first_type_errors = []
second_type_errors = []
for _ in range(10000):
control_aa, pilot_aa = get_random_data(
strats, sample_size, strat_to_param
)
control_ab, pilot_ab = get_random_data(
strats, sample_size, strat_to_param, effect
)
pvalue_aa = ttest_strat(control_aa, pilot_aa, weights)
first_type_errors.append(pvalue_aa < alpha)
pvalue_ab = ttest_strat(control_ab, pilot_ab, weights)
second_type_errors.append(pvalue_ab >= alpha)
part_first_type_errors = np.mean(first_type_errors)
part_second_type_errors = np.mean(second_type_errors)
print(f'part_first_type_errors = {part_first_type_errors:0.3f}')
print(f'part_second_type_errors = {part_second_type_errors:0.3f}')part_first_type_errors = 0.051
part_second_type_errors = 0.034Получили результаты практически совпадающие с экспериментом со стратификаций, где использовали стратифицированное семплирование. Получается, можно не делать стратифицированное семплирование, а ограничиться лишь использованием стратифицированного среднего? Всегда ли это так? Чтобы ответить на эти вопросы, посмотрим на стратификацию и постстратификацию с точки зрения математики.
Выпишем дисперсии средних для всех рассмотренных методов. Чем меньше дисперсия метрики, тем чувствительнее тест.
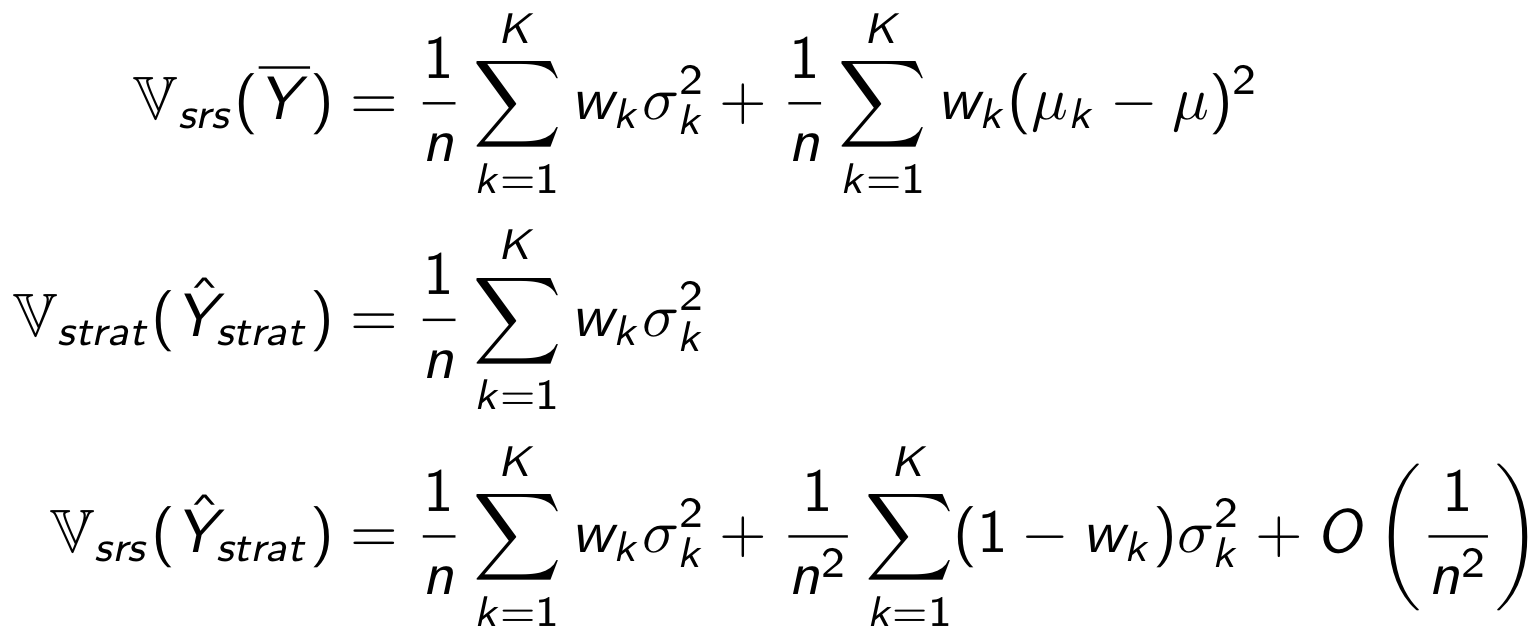
Индексы srs и strat у дисперсии означают способ семплирования данных - случайное и стратифицированное соответственно.
Вывод формул
Дисперсия обычного среднего при случайном семплирования может быть представлена в виде суммы дисперсий внутри стратифицированных групп, и между стратифицированными группами.
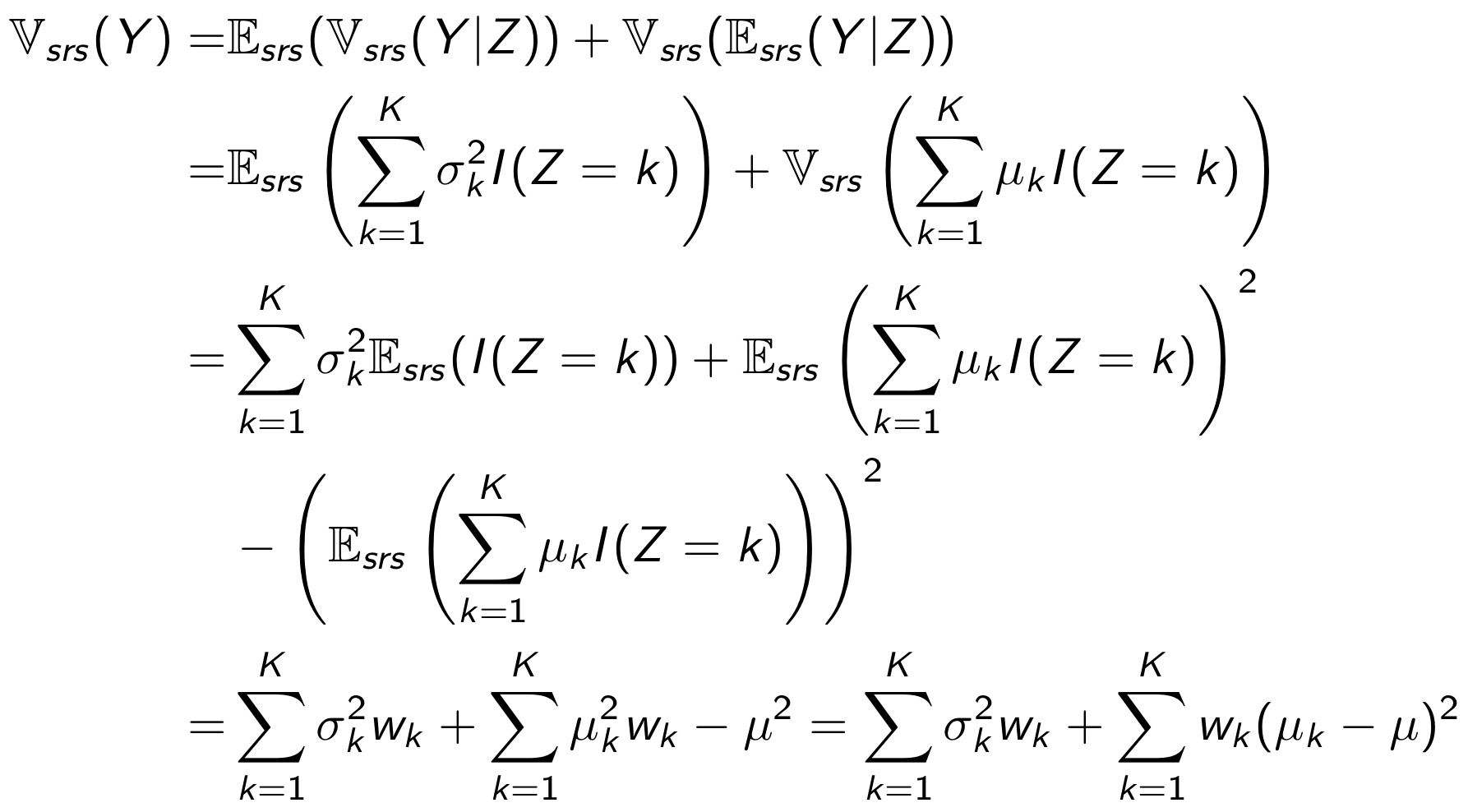
Выражение для дисперсии стратифицированного среднего при стратифицированном семплировании можно получить следующим образом:
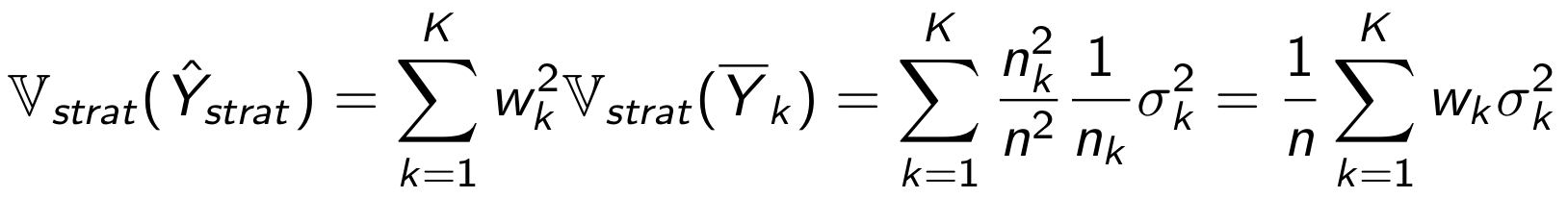
Осталось посчитать дисперсию стратифицированного среднего для случайного семплирования.
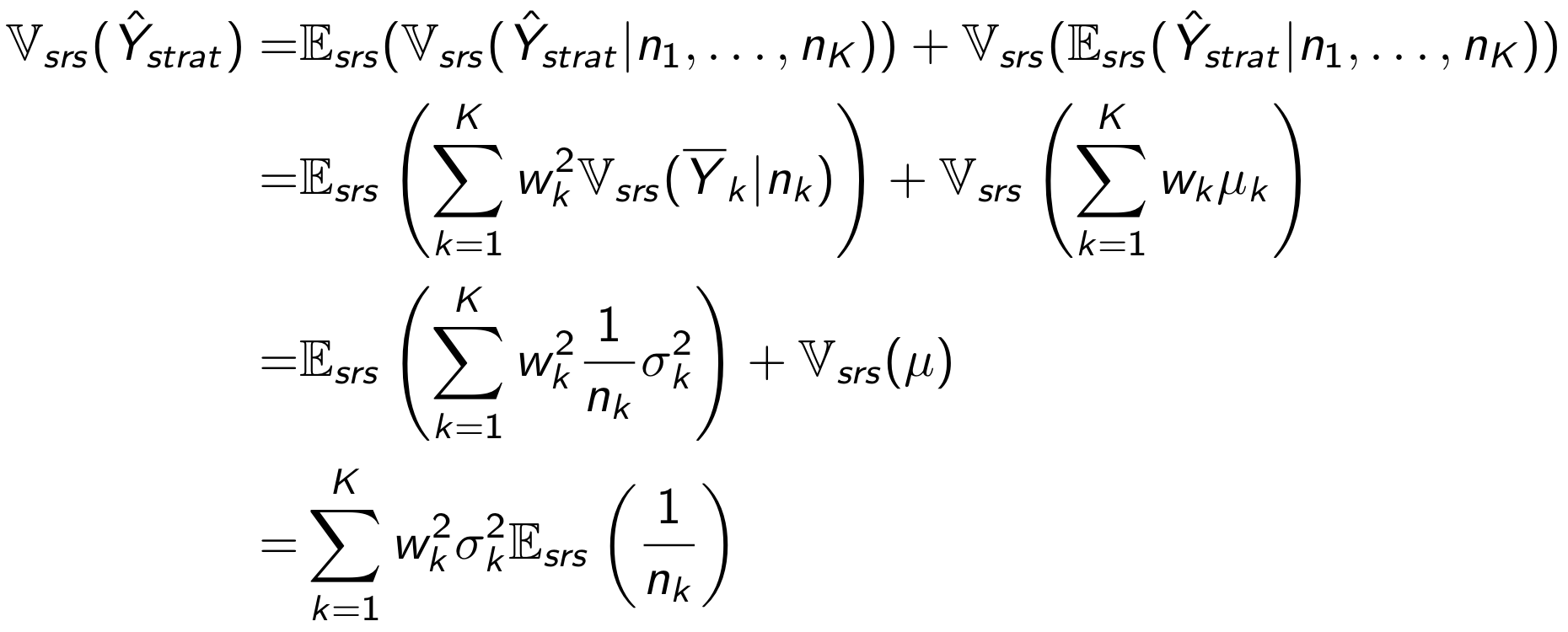

Получаем следующие соотношения
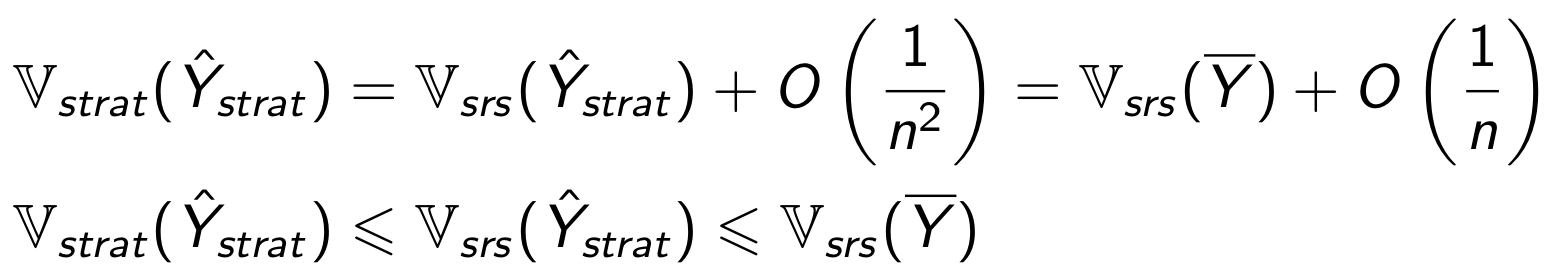
Дисперсия метрики при стратификации и постстратификации отличается на О(1/ n²). Значит, при достаточно большом объёме данных отличия между ними будут минимальны. В нашем примере размеры групп были порядка 1000, этого хватило, чтобы оценки вероятностей ошибок были практически одинаковыми.
Заметим, что стратификация повышает чувствительность теста только при отличии средних значений метрики между стратами. Как выбрать признаки для разбиения на страты? В общем случае ответа на этот вопрос нет, всё сильно зависит от решаемой задачи и специфики данных. Чтобы подобрать наиболее оптимальный вариант можно перебирать различные способы разбиения на страты и проверять на исторических данных как это влияет на вероятность ошибки первого рода и чувствительность теста. Но не стоит увлекаться перебором параметров, чтобы не допустить искусственного снижения дисперсии за счет появления ложной корреляции.
Итоги
Мы изучили стратификацию и постстратификацию. В нашем примере эти методы позволили снизить вероятность ошибки II рода более чем в 4 раза, контролируя вероятность ошибки I рода на заданном уровне. На практике повышение чувствительности тестов позволяет быстрее проводить эксперименты и находить эффекты меньшего размера, что является весомым конкурентным преимуществом.
Полезные материалы: Improving the Sensitivity of Online Controlled Experiments: Case Studies at Netflix
Авторы: Николай Назаров, Александр Сахнов

