Может показаться откровенной наглостью в наши дни утверждать, что Вы изобрели алгоритм сортировки, который на 30% быстрее, чем лучший существующий. Увы, я должен сделать гораздо более наглое заявление: я написал алгоритм сортировки, который в два раза быстрее, чем std :: sort для многих входных данных. И за исключением случаев, когда я специально конструирую воспроизведение наихудших для него ситуаций, алгоритм никогда не бывает медленнее, чем std :: sort (и даже когда попадаются эти худшие случаи, они обнаруживаются и происходит автоматический возврат к std :: sort)

Почему это утверждение неудачное? Потому что мне, вероятно, будет сложно убедить вас в том, что я ускорил сортировку в два раза. Однако (чтобы всех убедить – перев.) всё это должно теперь оказаться (описанным – перев.) довольно длинным сообщением в блоге, а весь исходный код - открытым кодом, чтобы вы могли опробовать его на любых данных. Так что я либо могу убедить вас множеством аргументов и измерений, либо вы можете просто опробовать алгоритм сами.

Следуя (будучи продолжением – перев.) за моим предыдущим сообщением в блоге, (в статье автор неоднократно ссылается на своё предыдущее сообщение в блоге, описывающее его взгляд на классический Radix sort - прим. перев.) конечно же, это версия Radix sort. Что означает, что его сложность ниже, чем O (n log n). Я сделал два усовершенствования:

• оптимизировал внутренний цикл поразрядной сортировки на месте. Я начал с реализации сортировки по американскому флагу в Википедии, и сделал некоторые неочевидные улучшения. Это делает сортировку Radix намного быстрее, чем std :: sort, даже для относительно небольших коллекций (от 128 элементов)

• обобщил поразрядную сортировку на месте для работы с целыми числами произвольного размера, числами с плавающей запятой, кортежами, структурами, векторами, массивами, строками и т. д. Я могу отсортировать все, что доступно с помощью операторов произвольного доступа, таких как operator [] или std :: get. Если у вас есть настраиваемые структуры, вам просто нужно предоставить функцию, которая может извлекать ключ, который вы хотите отсортировать. Это тривиальная функция, которая менее сложна, чем оператор сравнения, который вам придется написать для std :: sort.

Если вы просто хотите опробовать алгоритм, переходите к разделу «Исходный код и использование».

O (N) сортировка

Для начала я объясню, как вы можете построить алгоритм сортировки O (n). Если вы читали мой предыдущий пост в блоге, можете пропустить этот раздел. Если нет, читайте дальше:

Если вы типа меня месяц назад, вы точно знали, что доказано, что самый быстрый из возможных алгоритмов сортировки должен быть O (n log n). Есть математические доказательства того, что быстрее ничего не сделать. Я верил в это, пока не посмотрел вот эту лекцию из класса «Введение в алгоритмы» на MIT Open Course Ware. Там профессор объясняет, что сортировка должна быть O (n log n), когда все, что вы можете делать, это сравнивать элементы. Но если вам разрешено выполнять больше операций, чем просто сравнения, вы можете ускорить алгоритмы сортировки.

Я покажу пример с использованием алгоритма сортировки подсчетом:

template<typename It, typename OutIt, typename ExtractKey>
void counting_sort(It begin, It end, OutIt out_begin, ExtractKey && extract_key)
{
    size_t counts[256] = {};
    for (It it = begin; it != end; ++it)
    {
        ++counts[extract_key(*it)];
    }
    size_t total = 0;
    for (size_t & count : counts)
    {
        size_t old_count = count;
        count = total;
        total += old_count;
    }
    for (; begin != end; ++begin)
    {
        std::uint8_t key = extract_key(*begin);
        out_begin[counts[key]++] = std::move(*begin);
    }
}

Эта версия алгоритма может сортировать только символы без знака. Или, скорее, он может сортировать только типы, которые могут предоставить ключ сортировки, который является беззнаковым символом. В противном случае мы бы индексировали вне допустимого диапазона в первом цикле. Позвольте мне объяснить, как работает алгоритм:

У нас есть три массива и три цикла. У нас есть входной массив, выходной массив и счетный массив. В первом цикле мы заполняем счетный массив, перебирая входной массив, считая, как часто появляется каждый элемент.

Второй цикл превращает счетный массив в префиксную сумму счетчиков. Допустим, в массиве не 256 записей, а всего 8 записей. Допустим, числа выпадают так часто:

Итак, в этом случае всего было девять элементов. Номер 1 появился дважды, номер 2 появился один раз, номер 4 появился пять раз, а номер 5 появился один раз. Так что, возможно, входная последовательность была {4, 4, 2, 4, 1, 1, 4, 5, 4}.

Последний цикл снова перебирает исходный массив и использует ключ для поиска в массиве суммы префиксов. И, о чудо, этот массив сообщает нам конечную позицию, в которой нам нужно сохранить целое число. Итак, когда мы перебираем эту последовательность, 4 переходит в позицию 3, потому что это значение, которое сообщает нам массив суммы префиксов. Затем мы увеличиваем значение в массиве так, чтобы следующие 4 переместились в позицию 4. Число 2 переместится в позицию 2, следующие 4 переместятся в позицию 5 (потому что мы уже увеличили значение в массиве суммы префиксов дважды) и т. Д. Я рекомендую вам пройти через это один раз вручную, чтобы прочувствовать это. Конечным результатом этого должно быть {1, 1, 2, 4, 4, 4, 4, 4, 5}.

И вот так у нас есть отсортированный массив. Сумма префикса сообщила нам, где мы должны все хранить, и мы смогли вычислить это за линейное время.

Также обратите внимание, как это работает с любым типом, а не только с целыми числами. Все, что вам нужно сделать, это предоставить функцию extract_key () для вашего типа. В последнем цикле мы перемещаем указанный вами тип, а не ключ, возвращенный этой функцией. Так что это может быть любая настраиваемая структура. Например, вы можете отсортировать строки по длине. Просто используйте функцию size () в extract_key и ограничьте длину до 255. Вы можете написать модифицированную версию counting_sort, которая сообщает вам, где находится позиция последнего раздела, чтобы вы могли затем отсортировать все длинные строки с помощью std::sort (это должно быть небольшое подмножество всех ваших строк, чтобы второй проход по этим строкам был быстрым)

Сортировка на месте за линейное время

Вышеупомянутый алгоритм сохраняет отсортированные элементы в отдельном массиве. Но получить алгоритм сортировки на месте для беззнаковых символов ещё не весь фокус: мы могли бы попробовать, вместо того чтобы перемещать элементы менять их местами.

Самая очевидная проблема, с которой мы сталкиваемся, заключается в том, что когда мы меняем первый элемент с первой позиции, новый элемент, вероятно, не захочет быть на первой позиции. Вместо этого он может захотеть быть на позиции 10. Решение простое: продолжайте менять местами первый элемент, пока не найдем элемент, который действительно хочет (должен быть – прим.перев.) на первом месте. И только когда это произойдет, мы перейдем ко второму элементу массива.

Вторая проблема, с которой мы сталкиваемся, заключается в том, что мы обнаруживаем множество уже отсортированных разделов (частей массива – прим.перев.). Однако мы можем не знать, что они уже отсортированы. Представьте, что у нас есть число 3 два раза, и оно хочет быть на шестой и седьмой позициях. Допустим, при замене первого элемента на место мы меняем первые 3 на слот шесть, а вторые 3 на слот седьмой. Теперь они отсортированы, и нам больше не нужно с ними ничего делать. Но когда мы продвинемся от первого элемента, в какой-то момент мы встретим 3 в слоте шесть. И мы поменяем его местами на восьмерку, потому что это следующая точка, на которую попадет тройка. Затем мы находим следующие 3 и меняем их местами на девять. Затем мы снова находим первые 3 и меняем их местами на десять и т.д. Это продолжается до тех пор, пока мы не выйдем за границы массива и не сломаемся.

Решение второй проблемы состоит в том, чтобы сохранить копию исходного массива префиксов, чтобы мы могли определить, когда раздел завершен. Затем мы можем пропустить эти разделы при перемещении по массиву.

С этими двумя изменениями у нас получается алгоритм сортировки на месте, который сортирует символы без знака. Это сортировка типа американский флаг, описанная в Википедии.

RADIX сортировка на месте

Radix sort использует вышеуказанный алгоритм и обобщает его на целые числа, которые не помещаются в один символ без знака. Версия на месте фактически использует довольно простой трюк: сортируйте по одному байту за раз. Первая сортировка по старшему байту. Это разделит ввод на 256 разделов. Теперь рекурсивно отсортируйте в каждом из этих разделов, используя следующий байт. Продолжайте делать это, пока у вас не закончатся байты.

Если вы сделаете простые подсчёты, вы обнаружите, что для четырехбайтового целого числа вы получаете 256 ^ 3 рекурсивных вызовов: мы подразделяем на 256 разделов, затем рекурсивно, подразделяем каждый из них на 256 разделов и снова рекурсируем, а затем разделяем каждый из меньших разделов снова на 256 разделов и в последний раз выполняем рекурсию. Если бы мы действительно выполнили все эти рекурсии, это был бы очень медленный алгоритм. Способ обойти эту проблему - прекратить рекурсию, когда количество элементов в разделе меньше некоторого магического числа, и вместо этого использовать std :: sort внутри этого подраздела. В моем случае я прекращаю рекурсию, когда размер раздела меньше 128 элементов. Когда я разбиваю массив на разделы с меньшим количеством элементов, я вызываю std :: sort внутри этих разделов.

Если вам интересно: причина, по которой порог равен 128, заключается в том, что я делю вход на 256 разделов. Если количество разделов равно k, то сложность сортировки по одному байту составляет O (n + k). Точка, в которой сортировка radix выполняется быстрее, чем std :: sort, - это когда цикл, зависящий от n, начинает преобладать над циклом, который зависит от k. В моей реализации это где-то около 0,5 тыс. Нелегко переместить его намного ниже (есть идеи, но пока ничего не работает).

Обобщение RADIX сортировки

Должно быть ясно, что алгоритм, описанный в предыдущем разделе, работает для беззнаковых целых чисел любого размера. Но он также работает и для коллекций целых чисел без знака (включая пары и кортежи) и строк. Просто отсортируйте по первому элементу, затем по следующему, затем по следующему и т.д., пока размеры разделов не станут достаточно маленькими (на самом деле публикация, которую Википедия называет источником своей статьи «Сортировка американский флаг», рассматривала этот алгоритм как алгоритм сортировки строк).

Но это просто обобщить для работы со знаковыми целыми числами: просто переместите все значения вверх в диапазон беззнакового целого того же размера. Значение для int16_t просто приведите к uint16_t и добавьте 32768.

Майкл Херф также обнаружил хороший способ обобщить это для чисел с плавающей запятой: переинтерпретировать преобразование числа с плавающей запятой в uint32, затем перевернуть каждый бит, если число с плавающей запятой было отрицательным, но перевернуть только знаковый бит, если число с плавающей запятой было положительным. Тот же трюк работает с double и uint64s. Майкл Херф объясняет, почему это работает в публикации по ссылке, вкратце это выглядит так: положительные числа с плавающей запятой уже сортируются правильно, если мы просто переинтерпретируем их приведение к uint32. Показатель степени стоит перед мантиссой, поэтому мы будем сначала отсортировывать по экспоненте, а затем по мантиссе. Все получается. Однако отрицательные числа с плавающей запятой будут сортироваться неправильно. Переворачивание всех битов на них исправляет это. Последняя оставшаяся проблема заключается в том, что положительные числа с плавающей запятой необходимо сортировать как бОльшие, чем отрицательные, и самый простой способ сделать это - перевернуть знаковый бит, поскольку это самый старший бит.

Из основных типов остаются только логические значения и различные типы символов. Символы можно просто повторно интерпретировать в беззнаковые типы того же размера. Логические значения также можно преобразовать в беззнаковые символы, но мы также можем использовать специальный, более эффективный алгоритм для логических значений: просто используйте std :: partition вместо обычного алгоритма сортировки. И если нам нужно выполнить рекурсию, потому что мы сортируем более чем по одному ключу, мы можем выполнить рекурсию в каждую из секций.

И точно так же мы обобщили сортировку по основанию для всех типов. Теперь все, что нужно, - это магия шаблонов, чтобы заставить код работать правильно для каждого случая. Я избавлю вас от этих подробностей. Это было не весело.

Оптимизация внутреннего цикла

Краткое описание алгоритма сортировки для сортировки одного байта:

• Подсчитайте элементы и создайте префиксную сумму, которая сообщает нам, где разместить элементы.

• Поменяйте местами первый элемент с другими, пока не найдется элемент, который заслуживает быть на первой позиции (в соответствии с суммой префикса)

• Повторите шаг 2 для всех позиций.

Я реализовал этот алгоритм сортировки, используя визуализации озвученные сортировки Тимо Бингманна (Sound of Sorting - Timo Bingmann). - . Вот как это выглядит (и звучит):

Как видно из видео, большую часть времени алгоритм тратит на первую пару элементов. Иногда массив в основном сортируется во времени, когда алгоритм продвигается вперед от первого элемента. То, что вы не увидите на видео, - это массив суммы префиксов, построенный дополнительно. Визуализация (этого массива) сделала бы алгоритм более понятным (прояснило бы, как алгоритм может знать конечное положение элементов, чтобы поменять их прямо там), но я не сделал эту визуализацию.

Если мы хотим отсортировать несколько байтов, мы рекурсивно переходим к каждому из 256 разделов и выполняем сортировку в тех, которые используют следующий байт. Но это не самая медленная часть. Медленная часть - это шаг 2 и шаг 3.

Если вы отпрофилируете этот код, вы обнаружите, что он тратит все свое время на обмен элементов местами. Сначала я подумал, что это из-за промахов кеша. Обычно, когда строка сборки, занимающая много времени, разыменовывает указатель, это промах в кэше. Я объясню, в чем была настоящая проблема, ниже, но даже при том, что моя интуиция ошиблась, это подтолкнуло меня к хорошему ускорению: если у нас есть промах в кэше для первого элемента, почему бы не попробовать поставить второй элемент на место во время ожидания для кеша промахнулись по первому?

Мне уже нужно хранить информацию о том, какие элементы поменялись местами, поэтому я могу их пропустить. Итак, что я делаю, так это перебираю все элементы, которые еще не были переставлены на свои места, и меняю их местами. За один проход по массиву это заменит как минимум половину всех элементов на свои места. Чтобы понять почему, давайте подумаем, как это работает в этом списке: {4, 3, 1, 2}: мы смотрим на первый элемент, 4, и меняем его местами на 2 в конце, давая нам следующий список: {2 , 3, 1, 4}, затем мы смотрим на второй элемент, 3, и меняем его местами на 1, давая нам следующий список: {2, 1, 3, 4}, затем оказывается, что мы прошли итерацию на полпути по списку и обнаруживаем, что все оставшиеся элементы отсортированы (мы делаем это, проверяя, что смещение, сохраненное в массиве суммы префиксов, такое же, как начальное смещение следующего раздела), поэтому мы закончили, но наш список не отсортирован. Чтобы решить эту проблему, можно например, когда мы дойдем до конца списка, просто начать с самого начала, заменив все несортированные элементы на свои места. В этом случае нам нужно только переставить 2 на место, чтобы получить {1, 2, 3, 4}, после чего мы знаем, что все разделы отсортированы, и можно остановиться.

В Sound of Sorting это выглядит так:

Детали реализации

Вот как выглядит приведенный выше алгоритм в коде:

struct PartitionInfo
{
    PartitionInfo()
        : count(0)
    {
    }
 
    union
    {
        size_t count;
        size_t offset;
    };
    size_t next_offset;
};
 
template<typename It, typename ExtractKey>
void ska_byte_sort(It begin, It end, ExtractKey & extract_key)
{
    PartitionInfo partitions[256];
    for (It it = begin; it != end; ++it)
    {
        ++partitions[extract_key(*it)].count;
    }
    uint8_t remaining_partitions[256];
    size_t total = 0;
    int num_partitions = 0;
    for (int i = 0; i < 256; ++i)
    {
        size_t count = partitions[i].count;
        if (count)
        {
            partitions[i].offset = total;
            total += count;
            remaining_partitions[num_partitions] = i;
            ++num_partitions;
        }
        partitions[i].next_offset = total;
    }
    for (uint8_t * last_remaining = remaining_partitions + num_partitions, * end_partition = remaining_partitions + 1; last_remaining > end_partition;)
    {
        last_remaining = custom_std_partition(remaining_partitions, last_remaining, [&](uint8_t partition)
        {
            size_t & begin_offset = partitions[partition].offset;
            size_t & end_offset = partitions[partition].next_offset;
            if (begin_offset == end_offset)
                return false;
 
            unroll_loop_four_times(begin + begin_offset, end_offset - begin_offset, [partitions = partitions, begin, &extract_key, sort_data](It it)
            {
                uint8_t this_partition = extract_key(*it);
                size_t offset = partitions[this_partition].offset++;
                std::iter_swap(it, begin + offset);
            });
            return begin_offset != end_offset;
        });
    }
}

Алгоритм начинается так же, как и сортировка подсчета выше: я считаю, сколько элементов попадает в каждую секцию. Но я изменил второй цикл: во втором цикле я встраиваю массив индексов во все разделы, в которых есть хотя бы один элемент. Мне это нужно, потому что мне нужен способ отслеживать все разделы, которые еще не были завершены. Также я сохраняю конечный индекс для каждого раздела в переменной next_offset. Это позволит мне проверить, завершена ли сортировка раздела.

Третий цикл намного сложнее сортировки со счетом. Это три вложенных цикла, и только самый внешний является нормальным для цикла for:

Внешний цикл перебирает все оставшиеся несортированные разделы. Он останавливается, когда остается только один несортированный раздел. Этот предыдущий раздел не нужно сортировать, если все остальные разделы уже отсортированы. Это важная оптимизация, потому что случай, когда все элементы попадают только в один раздел, довольно распространен: при сортировке четырехбайтовых целых чисел, если все целые числа маленькие, то при первом вызове этой функции, которая сортирует по старшему байту, все ключи будут иметь одинаковое значение и попадут в один раздел. В этом случае этот алгоритм немедленно перейдет к следующему байту.

Средний цикл использует std :: partition для удаления завершенных разделов из списка оставшихся разделов. Я использую специальную версию std :: partition, потому что std :: partition развернет свой внутренний цикл, а я этого не хочу. Вместо этого мне нужно развернуть самый внутренний цикл. Но поведение custom_std_partition идентично поведению std :: partition. Этот цикл означает, что если элементы попадают в разделы разного размера, например, для входной последовательности {3, 3, 3, 3, 2, 5, 1, 4, 5, 5, 3, 3, 5, 3, 3}, где разделы для 3 и 5 больше, чем для других разделов, это очень быстро завершит разделы для 1, 2 и 4, а затем после этого внешний цикл и внутренний цикл должны пройти только по разделам для 3 и 5. Вы могли подумать, что я мог бы использовать здесь std :: remove_if вместо std :: partition, но мне нужно, чтобы действие было неразрушающим, потому что мне понадобится тот же список разделов при выполнении рекурсивных вызовов. (не показано в этом листинге кода)

Самый внутренний цикл, наконец, меняет местами элементы. Он просто перебирает все оставшиеся несортированные элементы в разделе и меняет их местами в их окончательную позицию. Это был бы обычный цикл for, за исключением того, что нужно развернуть этот цикл, чтобы получить высокую скорость. Поэтому я написал функцию под названием «unroll_loop_four_times», которая принимает итератор и счетчик цикла, а затем разворачивает цикл.

Почему это быстрее

Этот новый алгоритм сразу оказался намного быстрее, чем сортировка по американскому флагу. Что имело смысл, потому что я думал, что обманул промахи кеша. Но как только я отпрофилировал код, я заметил, что этот новый алгоритм сортировки на самом деле имел немного больше промахов в кэше. Также было больше ошибочных предсказаний ветвей. Он также выполнил больше инструкций. Но как-то на это ушло меньше времени. Это было довольно загадочно, поэтому я описал это как только мог. Например, я запустил его в Valgrind, чтобы увидеть, что, по мнению Valgrind, должно происходить. В Valgrind этот новый алгоритм был на самом деле медленнее, чем сортировка по американскому флагу. В этом есть смысл: Valgrind - это просто симулятор, поэтому что-то, что выполняет больше инструкций, имеет немного больше промахов в кеше и немного больше неверных предсказаний ветвлений, будет медленнее. Но почему бы ему быстрее работать на реальном оборудовании?

Мне потребовалось больше дня, на разглядывание чисел при профилировании кода, прежде чем я понял, почему это было быстрее: лучше параллелизм на уровне инструкций. Вы не могли бы изобрести этот алгоритм на старых компьютерах, потому что на старых компьютерах он был бы медленнее. Большая проблема с сортировкой по американскому флагу заключается в том, что ей нужно дождаться завершения текущего свопа, прежде чем он сможет начаться при следующем обмене. Не имеет значения, что нет промаха в кэше: современные процессоры могут выполнять несколько свопов одновременно, если только им не нужно ждать завершения предыдущего. Развертывание внутреннего цикла также помогает в этом. Современные процессоры великолепны, поэтому они могут запускать несколько циклов параллельно даже без развертывания цикла, но развертывание цикла помогает.

Команда perf в Linux имеет метрику, называемую «инструкций за такт», которая измеряет параллелизм на уровне инструкций. В сортировке по американскому флагу мой процессор выполняет 1,61 инструкции за такт. В этом новом алгоритме сортировки он достигает 2,24 инструкций за такт. Неважно, нужно ли вам выполнить дополнительно еще несколько инструкций, если вы можете делать на 40% больше за единицу времени.

Проблема с промахами в кэше и неверными предсказаниями ветвлений оказалась отвлекающим маневром: их значения на самом деле очень низкие для обоих алгоритмов. Таким образом, небольшое увеличение, которое я увидел, было небольшим увеличением до небольшого числа. Поскольку существует только 256 возможных точек вставки, есть вероятность, что значительная их часть всегда будет в кеше. А для многих реальных входных данных количество возможных точек вставки будет намного меньше. Например, при сортировке строк обычно получается меньше тридцати, потому что мы просто не используем так много разных символов.

При этом для небольших коллекций сортировка по американскому флагу выполняется быстрее. Кажется, что параллелизм на уровне инструкций действительно применяется в коллекциях из более чем тысячи элементов. Итак, мой окончательный алгоритм сортировки на самом деле смотрит на количество элементов в коллекции, и если оно меньше 128, я вызываю std :: sort, если меньше 1024, я вызываю сортировку по американскому флагу, а если больше этого, я запускаю свой новый алгоритм сортировки.

std :: sort на самом деле представляет собой аналогичную комбинацию, сочетающую быструю сортировку, сортировку вставкой и сортировку кучей, поэтому в некотором смысле они также являются частью моего алгоритма. Если бы я достаточно постарался, я мог бы построить входную последовательность, которая фактически использует все эти алгоритмы сортировки. Эта входная последовательность была бы моим наихудшим случаем: мне пришлось бы вызвать наихудшее поведение сортировки по основанию, чтобы мой алгоритм вернулся к std :: sort, а затем мне также пришлось бы запустить наихудшее поведение быстрой сортировки, поэтому этот std :: sort возвращается к сортировке кучей. Итак, давайте поговорим о худших и лучших случаях.

Лучший и худший случай

Наилучший случай для моей реализации сортировки по основанию - это если входные данные помещаются в несколько разделов. Например, если у меня есть тысяча элементов, и все они попадают только в три раздела (скажем, у меня просто число 1 сто раз, число 2 - четыреста раз и число 3 - пятьсот раз), тогда мои внешние циклы почти ничего не делают, и мой внутренний цикл может переставить все на свои места в красивых длинных непрерывных прогонах.

Мой другой лучший случай - это уже отсортированные последовательности: в этом случае я перебираю данные ровно дважды: один раз для просмотра каждого элемента и один раз для замены каждого элемента самим собой.

Наихудший случай для моей реализации может быть достигнут только при сортировке данных переменного размера, таких как строки. Для ключей фиксированного размера, таких как целые числа или числа с плавающей запятой, я не думаю, что это действительно плохой случай для моего алгоритма. Один из способов построить наихудший случай - отсортировать строки «a», «ab», «abc», «abcd», «abcde», «abcdef» и т.д. Так как radix sort просматривает один байт за раз, и это byte позволяет выделить из себя только один элемент, это займет время O (n ^ 2). Моя реализация определяет это, записывая, сколько было рекурсивных вызовов. Если их слишком много, я возвращаюсь к std :: sort. В зависимости от вашей реализации быстрой сортировки это также может быть худшим случаем для быстрой сортировки, и в этом случае std :: sort возвращается к сортировке кучей. Я кратко отладил это, и мне показалось, что std :: sort не вернулся к сортировке кучей для моего тестового примера. Причина этого в том, что в моем тестовом примере были отсортированные данные, а std :: sort, похоже, использует правило медианы трех для выбора точки поворота, которое выбирает хорошую точку поворота для уже отсортированных последовательностей. Зная это, вероятно, можно создать последовательности, которые попадут в наихудший случай как для моего алгоритма, так и для быстрой сортировки, используемой в std :: sort, и в этом случае алгоритм вернется к сортировке кучей. Но я не пытался построить такую ​​последовательность.

Я не знаю, насколько распространен этот случай в реальном мире, но одна уловка, которую я взял из реализации ускоренной реализации поразрядной сортировки, заключается в том, что я пропускаю общие префиксы. Итак, если вы сортируете сообщения журнала и у вас много сообщений, начинающихся с «warning:» или «error:», то моя реализация Radix-сортировки сначала отсортирует их по отдельным разделам, а затем внутри каждого из этих разделов будет пропускать общий префикс и продолжать сортировку с первого отличающегося символа. Такое поведение должно помочь снизить частоту возникновения наихудшего случая.

В настоящее время я возвращаюсь к std :: sort, если мой код повторяется более шестнадцати раз. Я выбрал это число, потому что это была первая степень двойки, для которой определение наихудшего случая не срабатывало при сортировке некоторых файлов журнала на моем компьютере.

Резюме алгоритма и его наименование

Алгоритм сортировки, который я предоставляю в виде библиотеки, называется «Ska Sort». Потому что я не собираюсь придумывать новые алгоритмы очень часто в своей жизни, так что я с таким же успехом могу поставить свое имя на одном из них, когда его (этот новый достойный алгоритм) сделаю. Улучшенный алгоритм сортировки байтов, который я описал выше в разделах «Оптимизация внутреннего цикла» и «Детали реализации», является лишь небольшой частью этого (домена моих алгоритмов). Алгоритм называн «Ska Byte Sort».

Таким образом, Ska Sort:

• Алгоритм сортировки по основанию на месте

• Сортирует по одному байту (на 256 разделов)

• Возвращается к std :: sort, если коллекция содержит меньше некоторого порога элементов (в настоящее время 128)

• Использует внутренний цикл сортировки по американскому флагу, если коллекция содержит меньше большего порога элементов (в настоящее время 1024)

• Использует Ska Byte Sort, если коллекция больше этого (порога - перев.)

• Вызывает себя рекурсивно для каждого из 256 разделов, используя следующий байт в качестве ключа сортировки

• Возвращается к std :: sort, если он повторяется слишком много раз (в настоящее время 16 раз)

• Использует std :: partition для сортировки логических значений

• Автоматически преобразует целые числа со знаком, числа с плавающей запятой и типы символов в правильный целочисленный тип без знака

• Автоматически обрабатывает пары, кортежи, строки, векторы и массивы, сортируя по одному элементу за раз

• Пропускает общие префиксы коллекций (например, при сортировке строк)

• Предоставляет две точки настройки для извлечения ключа сортировки из объекта: объект функции, который может быть передан в алгоритм, или функция с именем to_radix_sort_key (), которую можно поместить в пространство имен вашего типа.

Итак, Ska Sort - сложный алгоритм. Конечно, сложнее простой быстрой сортировки. Одна из причин этого заключается в том, что в Ska Sort у меня гораздо больше информации о типах, которые я сортирую. В алгоритмах сортировки на основе сравнения все, что у меня есть, - это функция сравнения, которая возвращает логическое значение. В Ska Sort я могу знать, что «для этой коллекции мне сначала нужно выполнить сортировку по логическому значению, а затем по плавающему значению», и я могу написать собственный код для обоих этих случаев. На самом деле мне часто нужен собственный код: код, сортирующий кортежи, должен отличаться от кода, сортирующего строки. Конечно, у них один и тот же внутренний цикл, но им обоим нужно выполнять разную работу, чтобы добраться до этого внутреннего цикла. При сортировке на основе сравнения вы получаете одинаковый код для всех типов.

Оптимизации, которых я не делал

Если у вас достаточно времени, чтобы пощелкать по ссылкам, приведенным выше, вы обнаружите, что есть две оптимизации, которые считаются важными в моих источниках, которых я не делал.

Во-первых, часть, в которой говорится о сортировке чисел с плавающей запятой, сортирует 11 бит за раз, а не по одному байту за раз. Это означает, что он делит диапазон на 2048 разделов вместо 256 разделов. Преимущество здесь заключается в том, что вы можете отсортировать четырехбайтовое целое число (или четырехбайтовое число с плавающей запятой) за три прохода вместо четырех. Я опробовал это в своем (упоминавшемся ранее - перев.) предыдущем сообщении в блоге и обнаружил, что это работает быстрее только в некоторых случаях. В большинстве случаев это было медленнее, чем сортировка по одному байту за раз. Возможно, стоит попробовать еще раз этот трюк для сортировки по основанию счисления на месте, но я этого не делал.

Во-вторых, в статье American Flag Sort говорится об управлении рекурсиями вручную. Вместо того, чтобы делать рекурсивные вызовы, они хранят стек всех разделов, которые еще нужно отсортировать. Затем они зацикливаются, пока этот стек не станет пустым. Я не пробовал эту оптимизацию, потому что мой код и так слишком сложен. Эту оптимизацию проще выполнить, если вам нужно только отсортировать строки, потому что вы всегда используете одну и ту же функцию для извлечения текущего байта. Но если вы можете сортировать целые числа, числа с плавающей запятой, кортежи, векторы, строки и многое другое, это сложно.

Демонстрация производительности

Наконец, мы подошли к тому, насколько быстрым на самом деле является этот алгоритм. Со времени моего предыдущего сообщения в блоге я изменил способ вычисления этих чисел. В своем предыдущем сообщении в блоге я совершил большую ошибку: я измерил, сколько времени уходит на настройку моих тестовых данных и их сортировку. Проблема в том, что настройка может занимать значительную часть времени. Так что на этот раз я также измеряю настройку отдельно и вычитаю это время из измерений, так что у меня остается только время, необходимое для фактической сортировки данных. Итак, приступим к нашему первому измерению: Сортировка целых чисел: (сгенерировано с использованием std :: uniform_int_distribution)

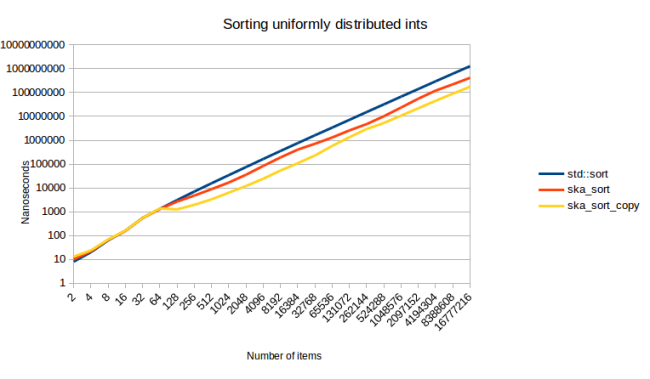
Этот график показывает, сколько времени занимает сортировка различного количества элементов. Раньше я не упоминал ska_sort_copy, но, по сути, это алгоритм из моего предыдущего сообщения в блоге, за исключением того, что я изменил его так, чтобы он возвращался к ska_sort вместо возврата к std :: sort. (ska_sort, конечно, может решить вернуться к std :: sort)

У меня есть одна проблема с этим графиком: даже несмотря на то, что я сделал шкалу логарифмической, все равно очень трудно увидеть, что происходит. В прошлый раз я добавил еще одну строку внизу, которая показывала относительный масштаб, но на этот раз у меня есть лучший подход. Вместо логарифмической шкалы я могу разделить общее время на количество элементов, чтобы получить время, которое алгоритм сортировки тратит на элемент:

С помощью этой визуализации мы можем гораздо яснее увидеть, что происходит. На всех рисунках ниже в качестве шкалы используется «наносекунды на элемент», как на этом графике. Давайте немного разберем этот график:

Для первой пары элементов мы видим, что линии практически одинаковы. Это потому, что для менее чем 128 элементов я возвращаюсь к std :: sort. Таким образом, вы ожидаете, что все строки будут точно такими же. Любая разница в этой области - это шум измерения.

Затем мы видим, что std :: sort - это в точности алгоритм сортировки O (n log n). Рост линейный, когда мы делим время на количество элементов, что является именно тем, чего вы могли бы ожидать от O (n log n). Реально впечатляет то, как она образует ровную прямую линию, после того, как количество (сортируемых) элементов превысит небольшое пороговое значение. ska_sort_copy - это действительно алгоритм сортировки O (n): стоимость одного элемента остается в основном постоянной по мере увеличения общего количества элементов. Но ska_sort… более сложный.

Волны, которые мы видим в строке ska_sort, связаны с количеством рекурсивных вызовов: ska_sort самый быстрый, когда количество элементов велико. Поэтому линия сначала убывает. Но затем в какой-то момент нам нужно рекурсивно создать кучу разделов размером чуть более 128 элементов, что происходит медленно. Затем эти разделы растут по мере увеличения количества элементов, и алгоритм снова работает быстрее, пока мы не дойдем до точки, где размер разделов снова превышает 128 элементов, и нам нужно добавить еще один рекурсивный шаг. Один из способов визуализировать это - посмотреть на график сортировки коллекции int8_t:

Как видите, вначале стоимость (сортировки - перев.) единичного значения резко снижается. Каждый раз, когда алгоритму приходится возвращаться к другим разделам, мы видим, что начальная часть кривой накладывается, давая нам волны графика для сортировки целых чисел.

Выше я отметил, что ska_sort работает быстрее всего, когда есть несколько разделов для сортировки элементов. Итак, давайте посмотрим, что происходит, когда мы используем std :: geometry_distribution вместо std :: uniform_int_distribution:

Этот график снова сортирует четыре байта int, поэтому вы ожидаете увидеть те же «волны», которые мы видели в равномерно распределенных int. Я использую std :: geometry_distribution с 0,001 в качестве аргумента конструктора. Это означает, что он генерирует числа от 0 до примерно 18000, но большинство чисел будут близки к нулю (теоретически он может генерировать числа, которые намного больше, но 18882 - это наибольшее число, которое я измерил при генерации вышеуказанных данных). И поскольку большинство чисел близки к нулю, мы увидим мало рекурсий, и из-за этого мы видим мало волн, делающих (алгоритм – перев.) во много раз быстрее, чем std :: sort.

Кстати, эта шишка в начале меня удивляет. Для всех остальных данных, которые мне удалось найти, ska_sort начинает опережать std :: sort на 128 элементах. Здесь вроде ska_sort начинает выигрывать только потом. Я не знаю почему. Я мог бы исследовать это в другой момент времени, но я не хочу менять порог, потому что это хорошее число для всех других данных. Изменение порога немного сдвинуло бы все остальные строки вверх. Кроме того, поскольку мы сортируем там несколько элементов, разница в абсолютном выражении не так велика: от 15,8 микросекунд до 16,7 микросекунд для 128 элементов и от 32,3 микросекунд до 32,9 микросекунд для 256 элементов.

Давайте рассмотрим еще несколько вариантов использования. Вот мой вариант использования в «реальном мире», о котором я говорил в предыдущем сообщении в блоге, где мне нужно было сортировать врагов в игре по расстоянию до игрока. Но я хотел, чтобы все враги, которые сейчас находятся в бою, были первыми, отсортированные по расстоянию, а затем все враги, которые не участвуют в бою, также отсортированные по расстоянию. Итак, я сортирую по std :: pair:

Это оказался тот же график, что и сортировка целых чисел, за исключением того, что каждая строка сдвинута на немного вверх. Чего, я полагаю, следовало ожидать. Но приятно видеть, что трюк с преобразованием, который я должен использовать для чисел с плавающей запятой, и разбиение, которое я должен выполнить для пар, не добавляют значительных накладных расходов. Более интересный график для сортировки int64:

Это момент, когда ska_sort_copy иногда работает медленнее, чем ska_sort. На самом деле я решил снизить порог, при котором ska_sort_copy возвращается к ska_sort: теперь он будет выполнять сортировку по основанию копирования только тогда, когда ему нужно выполнить менее восьми итераций по входным данным. Это означает, что я изменил код, так что для int64s ska_sort_copy на самом деле просто вызывает ska_sort. Основываясь на приведенном выше графике, вы можете утверждать, что он все равно должен выполнять сортировку по основанию счисления копирования, но вот измерение сортировки 128-байтовой структуры, которая имеет int64 в качестве ключа сортировки:

По мере увеличения структур ska_sort_copy становится медленнее. Из-за этого я решил заставить ska_sort_copy вернуться к ska_sort для ключей сортировки такого размера.

Еще одна вещь, на которую следует обратить внимание из приведенного выше графика, заключается в том, что похоже, что std :: sort и ska_sort (в некоторый момент прим.перев.) сближаются. Так ska_sort в какой-то момент становится медленнее? Не похоже. Вот как это выглядит, когда я сортирую 1024-байтовую структуру:

И снова это очень интересный график. Хотел бы я потратить время на то, чтобы выяснить, откуда взялся этот большой разрыв в конце. Это не шум измерения. Это воспроизводимо. Графики строились с запуском Google Benchmark тридцать раз, чтобы уменьшить вероятность случайного отклонения.

Говоря о больших данных, в моем предыдущем сообщении в блоге худшим случаем была (описана) сортировка структуры с 256-байтовым ключом сортировки. Что в данном случае означает использование std :: array в качестве ключа сортировки. Это было очень медленным при копирующей поразрядной сортировке, потому что на самом деле нам нужно сделать 256 проходов по данным. Поразрядная сортировка на месте должна проверять только достаточное количество байтов, пока не сможет различить два фрагмента данных, так что это может быть и быстрее. И если посмотреть на тесты, выглядит это так:

ska_sort_copy вернется к ska_sort для этого ввода, поэтому его график будет выглядеть идентично. Итак, я исправил худший случай из моего предыдущего сообщения в блоге. Одна вещь, которую я не мог описать в моем предыдущем сообщении в блоге, - это сортировка строк, потому что ska_sort_copy просто не может сортировать строки, потому что не может сортировать данные переменного размера.

Итак, давайте посмотрим, что происходит, когда я сортирую строки:

Здесь я создаю входные данные: беру от одного до трех случайных слов из своего файла слов и объединяю их. Еще раз я очень рад видеть, насколько хорошо работает мой алгоритм. Но этого следовало ожидать: уже было известно, что поразрядная сортировка отлично подходит для сортировки строк.

Но сортировка строк - это еще и тот случай, когда я могу попасть в худший вариант. Теоретически вы можете получить случаи, когда вам нужно сделать много проходов по данным, потому что во входных данных просто много байтов, и многие из них похожи. Итак, я попробовал, что происходит, когда я сортирую строки разной длины, объединяя от нуля до десяти слов из моего файла слов:

Здесь мы видим, что ska_sort, похоже, становится алгоритмом O (n log n) при сортировке миллионов длинных строк. Однако он не работает медленнее, чем std :: sort. Мое лучшее предположение для такой восходящей кривой - это то, что ska_sort должен выполнять много рекурсий с этими данными. Он не выполняет достаточно рекурсий, чтобы запустить мое обнаружение наихудшего случая, но эти рекурсии по-прежнему дороги, потому что они требуют еще одного прохода по данным.

Одна вещь, которую я пробовал, - это понизить предел рекурсии до восьми, и в этом случае я обнаружил худший случай, начиная с миллиона элементов. Но в этом случае график практически не изменится. Причина в том, что это ложное срабатывание: я не попал в худший вариант. Алгоритм сортировки все еще преуспел в разделении данных на множество более мелких разделов, поэтому, когда я возвращаюсь к std :: sort, ему гораздо легче, чем при сортировке всего диапазона.

Наконец, вот как это выглядит, когда я сортирую контейнеры, которые немного сложнее строк:

Для этого я генерирую векторы от 0 до 20 int. Итак, я сортирую вектор векторов. Этот всплеск в конце очень интересен. Мое обнаружение слишком большого количества рекурсивных вызовов здесь не срабатывает, поэтому я не уверен, почему сортировка становится намного дороже. Возможно, моему процессору просто не нравится иметь дело с таким большим объемом данных. Но я рад сообщить, что ska_sort быстрее, чем std :: sort, как и во всех других графиках.

Поскольку ska_sort кажется всегда быстрее, я также сгенерировал входные данные, которые намеренно запускают худший случай для ska_sort. На графике ниже показан наихудший случай, начиная с 128 элементов. Но ska_sort обнаруживает это и возвращается к std :: sort:

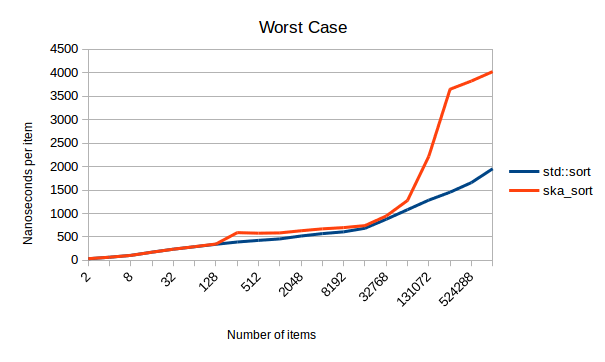
Для этого я сортирую случайные комбинации векторов {}, {0}, {0, 1}, {0, 1, 2},… {0, 1, 2,…, 126, 127}. Поскольку каждый элемент сообщает моему алгоритму только о том, как отделить 1/128 входных данных, ему придется выполнить рекурсию 128 раз. Но на шестнадцатой рекурсии ska_sort сдается и возвращается к std :: sort. На приведенном выше графике вы видите, сколько там накладных расходов. Накладные расходы больше, чем мне хотелось бы, особенно для больших коллекций, но для небольших коллекций они кажутся очень низкими. Я не рад, что эти накладные расходы существуют, но я рад, что ska_sort обнаруживает худший случай и, по крайней мере, не переходит в O (n ^ 2).

Проблемы

Ska_sort не идеален, и у него есть проблемы. Я верю, что он будет быстрее, чем std :: sort почти для всех данных, и его почти всегда следует предпочесть std :: sort.

Самая большая проблема - сложность кода. Особенно магия шаблонов для рекурсивной сортировки последовательных байтов. Так, например, в настоящее время при сортировке по std :: pair <int, int> это приведет к созданию экземпляра алгоритма сортировки восемь раз, потому что будет восемь различных функций для извлечения байта из этих данных. Я могу придумать способы уменьшить это число, но они могут быть связаны с накладными расходами во время выполнения. Это требует дополнительных исследований, но сложность кода также затрудняет такие изменения. Пока вы можете получить при этом медленную компиляцию, если ваш ключ сортировки сложный. Самый простой способ обойти это - попытаться использовать более простой ключ сортировки.

Другая проблема заключается в том, что я не уверен, что делать с данными, которые я не могу отсортировать. Например, этот алгоритм не может отсортировать вектор из std :: sets. Причина в том, что std :: set не имеет операторов произвольного доступа, и мне нужен произвольный доступ при сортировке по одному элементу за один раз. Я мог бы написать код, который позволяет мне сортировать std :: sets с помощью std :: advance на итераторах, но код может быть медленным. В качестве альтернативы я мог бы вернуться к std :: sort. Сейчас я не делаю ни того, ни другого: я просто выдаю ошибку компиляции. Причина в том, что я предоставляю точку настройки, функцию, называемую to_radix_sort_key (), которая позволяет вам писать собственный код для превращения ваших структур в сортируемые данные. Если бы я делал автоматический откат всякий раз, когда я не могу что-то отсортировать, использование этой точки настройки было бы более раздражающим: прямо сейчас вы получаете сообщение об ошибке, когда вам нужно его предоставить, и когда вы его предоставите, ошибка исчезнет. Если я вернусь к std :: sort для данных, которые я не могу отсортировать, ваше единственное замечание будет заключаться в том, что сортировка немного замедлится. Вам нужно будет либо профилировать этот код и сравнить с std :: sort, либо выполнить функцию сортировки, чтобы убедиться, что она действительно использует вашу реализацию to_radix_sort_key (). Так что пока я решил выдавать сообщение об ошибке, когда не могу отсортировать тип. Затем вы можете решить, хотите ли вы реализовать to_radix_sort_key () или хотите использовать std :: sort. или вам нужно будет выполнить функцию сортировки, чтобы убедиться, что она действительно использует вашу реализацию to_radix_sort_key ().

Так что пока я решил выдавать сообщение об ошибке, когда не могу отсортировать тип. Затем вы можете решить, хотите ли вы реализовать to_radix_sort_key () или хотите использовать std :: sort.

Другая проблема заключается в том, что сейчас может быть только одно поведение сортировки для каждого типа. Вы должны предоставить мне ключ сортировки, и если вы предоставите мне целое число, я буду отсортировать ваши данные в порядке возрастания. Если вы хотите, чтобы это было в порядке убывания, в настоящее время для этого нет простого интерфейса. Для целых чисел вы можете решить эту проблему, перевернув знак в ключевой функции, так что это может быть не так уж и плохо. Но со строками становится сложнее: если вы предоставите мне строку, я отсортирую строку с учетом регистра в порядке возрастания. В настоящее время нет возможности выполнять сортировку строк без учета регистра. (или, может быть, вам нужна сортировка с учетом (значений) чисел, чтобы «bar100» появлялось после «bar99», но прямо сейчас этого сделать нельзя). Я думаю, что это решаемая проблема, я просто еще не выполнил эту работу.

Исходный код и использование

Я загрузил код на github. Под лицензией Boost.

Интерфейс работает несколько иначе, чем другие алгоритмы сортировки. Вместо предоставления функции сравнения вы предоставляете функцию, которая возвращает ключ сортировки, который алгоритм сортировки использует для сортировки ваших данных. Например, предположим, что у вас есть вектор врагов, и вы хотите отсортировать их по расстоянию до игрока. Но вы хотите, чтобы все враги, которые находятся в бою с игроком, были первыми, отсортированные по расстоянию, а затем все враги, которые не участвуют в бою, также отсортированные по расстоянию. В классическом алгоритме сортировки это можно сделать так:

std::sort(enemies.begin(), enemies.end(), [](const Enemy & lhs, const Enemy & rhs)
{
    return std::make_tuple(!is_in_combat(lhs), distance_to_player(lhs))
         < std::make_tuple(!is_in_combat(rhs), distance_to_player(rhs));
});

Вместо этого в ska_sort вы бы сделали это так:

ska_sort(enemies.begin(), enemies.end(), [](const Enemey & enemy)
{
    return std::make_tuple(!is_in_combat(enemy), distance_to_player(enemy));
});

Как видите, преобразование довольно простое. Точно так же предположим, что у вас есть группа людей, и вы хотите отсортировать их по фамилии, а затем по имени. Вы могли сделать это:

ska_sort(contacts.begin(), contacts.end(), [](const Contact & c)
{
    return std::tie(c.last_name, c.first_name);
});

Здесь важно использовать std :: tie, потому что предположительно last_name и first_name являются строками, и вы не хотите их копировать. std :: tie захватит их по ссылке.

Ну и, конечно, если у вас есть просто вектор простых типов, вы можете просто отсортировать их напрямую:

ska_sort(durations.begin(), durations.end());

Здесь я предполагаю, что «длительности» - это вектор double, и вы можете захотеть отсортировать их, чтобы найти медиану, 90-й процентиль, 99-й процентиль и т.д. Поскольку ska_sort уже может сортировать double, никакого специального кода не требуется.

И последний случай - это сортировка коллекции настраиваемых типов. ska_sort принимает только одну функцию настройки, но что делать, если у вас есть вложенный пользовательский тип? В этом случае мой алгоритм должен был бы перейти к типу верхнего уровня, а затем натолкнуться на тип, который он не понимает. Когда это произойдет, вы получите сообщение об ошибке об отсутствии перегрузки для to_radix_sort_key (). Что вам нужно сделать, так это предоставить реализацию функции to_radix_sort_key (), которую можно найти с помощью ADL для вашего пользовательского типа:

struct CustomInt
{
    int i;
};
int to_radix_sort_key(const CustomInt & i)
{
    return i.i;
}
 
//... later somewhere
 
std::vector<std::vector<CustomInt>> collections = ...;
ska_sort(collections.begin(), collections.end());

В этом случае ska_sort вызовет to_radix_sort_key () для вложенных CustomInts. Вы должны сделать это, потому что нет эффективного способа предоставить пользовательскую функцию extract_key на верхнем уровне (на верхнем уровне вам нужно будет преобразовать std :: vector <CustomInt> в std :: vector <int>, а для этого потребуется копия)

Наконец, я также предоставляю копирующую функцию сортировки, ska_sort_copy, которая будет намного быстрее для маленьких ключей. Чтобы использовать её, вам необходимо предоставить второй буфер того же размера, что и входной буфер. Затем возвращаемое значение функции сообщит вам, находится ли окончательная отсортированная последовательность во втором буфере (функция возвращает истину) или в первом буфере (функция возвращает ложь).

std::vector<int> temp_buffer(to_sort.size());
if (ska_sort_copy(to_sort.begin(), to_sort.end(), temp_buffer.begin()))
    to_sort.swap(temp_buffer);

В этом коде я выделяю временный буфер, и если функция сообщает мне, что результат оказался во временном буфере, я меняю его на входной буфер. В зависимости от вашего варианта использования, возможно, вам не придется делать свопинг. И чтобы сделать это быстро, вам не нужно выделять временный буфер только для сортировки. Вы захотите повторно использовать этот буфер.

Вопросы-ответы

Я поговорил об этом с несколькими людьми, и все обычные вопросы, которые я получаю, связаны с людьми, которые не верят, что мой код на самом деле быстрее.

В: Разве Radix Sort не O (n + m), где m велико, так что на самом деле он медленнее, чем алгоритм O (n log n)? (или, по-другому: не является ли сортировка по основанию O (n * m), где m больше, чем log n?)

О: Да, сортировка radix имеет большие постоянные коэффициенты, но в моих тестах она начинает превосходить std :: sort при 128 элементах. А если у вас большая коллекция, скажем, тысяча элементов, радиксная сортировка станет явным победителем.

В: Разве Radix Sort не переходит в алгоритм O (n log n)? (или, по-другому: разве худший случай Radix Sort не O (n log n) или, может быть, даже O (n ^ 2)?)

A: В некотором смысле Radix Sort должен выполнять log (n) передач данных. При сортировке int16 вы должны выполнить два прохода по данным. При сортировке int32 вам нужно выполнить четыре прохода по данным. При сортировке int64 вам нужно выполнить восемь проходов и т.д. Однако это не O (n log n), потому что это постоянный коэффициент, не зависящий от количества элементов. Если я отсортирую тысячу int32, мне придется выполнить четыре прохода по этим данным. Если я отсортирую миллион int32, мне все равно придется сделать четыре прохода по этим данным. Объем работы растет линейно. И если целые числа в первом байте разные, мне даже не нужно делать второй, третий или четвертый проход. Мне всего лишь нужно сделать достаточно проходов, пока я не смогу их все отличить.

Таким образом, наихудший случай для сортировки по основанию - O (n * b), где b - это количество байтов, которые мне нужно прочитать, пока я не смогу различить все элементы по отдельности. Если вы заставите меня сортировать много длинных строк, то количество байтов может быть довольно большим, а сортировка по основанию может быть медленной. Это график «наихудшего случая» выше. Если у вас есть данные, в которых сортировка поразрядная выполняется медленнее, чем std :: sort (то, что я не мог найти, кроме случаев намеренного создания неверных данных), сообщите мне. Мне было бы интересно узнать, сможем ли мы найти какие-нибудь оптимизации для этих случаев. Когда я пытался построить более правдоподобные строки, ska_sort всегда был явно быстрее.

А если вы сортируете что-то фиксированного размера, например, числа с плавающей точкой, то худшего случая просто не может быть. Вы ограничены количеством байтов, и вы сделаете не более четырех проходов по данным.

В: Если бы эти графики производительности были верны, мы бы все сортировали поразрядно.

A: Они верны. Не знаю, что тебе сказать. Код находится на github , попробуйте сами. И да, я действительно ожидаю, что мы будем все сортировать по системе radix. Честно говоря, я не знаю, почему раньше все остановились на Quick Sort.

Планы на будущее

Есть несколько очевидных улучшений, которые я могу внести в алгоритм. Алгоритм в настоящее время находится в хорошем состоянии, но если мне когда-нибудь захочется поработать над этим снова, вот три вещи, которые я могу сделать:

Как я сказал в разделе проблем, в настоящее время нет способа сортировать строки без учета регистра. Добавить эту особенность не так уж сложно, но вам понадобится какой-то общий способ настройки поведения сортировки. В настоящее время все, что вы можете сделать, это указать собственный ключ сортировки. Но вы не можете изменить то, как алгоритм использует этот ключ сортировки. Вы всегда получаете элементы, отсортированные в порядке возрастания, просматривая по одному байту за раз.

Когда я возвращаюсь к std :: sort, я снова начинаю сортировку с самого начала. Как я уже сказал выше, я возвращаюсь к std :: sort, когда разбиваю ввод на разделы, содержащие менее 128 элементов. Но давайте предположим, что один из этих разделов - это все строки, начинающиеся с «warning:», а один раздел - это все строки, начинающиеся с «error:», тогда, когда я возвращаюсь к std :: sort, я мог бы пропустить общий префикс. У меня есть информация о том, сколько байтов уже отсортировано. Я подозреваю, что тот факт, что std :: sort должен начинаться с самого начала, является причиной того, почему линии в графе для сортировки строк настолько параллельны между ska_sort и std :: sort. Эта оптимизация может значительно ускорить откат к std :: sort.

Я мог бы также захотеть написать функцию, которая может принимать либо функцию сравнения, либо функцию extract_key. Это будет работать следующим образом: если вы передадите объект функции, который принимает два аргумента, будет использована сортировка на основе сравнения, а если вы передадите объект функции, который принимает один аргумент, будет использована сортировка поразрядная. Причина создания такой функции заключается в том, что она может быть обратно совместима с std :: sort.

Заключение

В итоге у меня есть алгоритм сортировки, который быстрее, чем std :: sort для большинства входных данных. Алгоритм сортировки находится на github и под лицензией boost, так что пробуйте.

В основном я сделал две вещи:

• Я оптимизировал внутренний цикл поразрядной сортировки на месте, в результате получился алгоритм ska_byte_sort

• Я предоставляю алгоритм ska_sort, который может выполнять сортировку Radix для произвольных типов или комбинаций типов.

Чтобы использовать его в настраиваемых типах, вам необходимо предоставить функцию, которая предоставляет «ключ сортировки» для ska_sort, который должен быть int, float, bool, vector, string, кортежем или парой, состоящей из одного из них. Список поддерживаемых типов велик: подойдет любой примитивный тип или что угодно с operator [], поэтому std :: array, std :: deque и другие также будут работать.

Если сортировка данных имеет решающее значение для производительности вашего кода (вполне вероятно, что это так, учитывая, насколько важна сортировка для нескольких других алгоритмов), вам следует попробовать этот алгоритм. Он самый быстрый при сортировке большого количества элементов, но даже для небольших коллекций он никогда не медленнее, чем std :: sort (потому что он использует std :: sort, когда коллекция слишком мала)

Основные уроки, которые следует извлечь, заключаются в том, что даже «решенные» проблемы, такие как сортировка, стоит время от времени пересматривать. И всегда хорошо изучать основы как следует. Я и не ждал, что постигну что-нибудь на курсе «Введение в алгоритмы», но на сей день (всё таки) написал данный алгоритм, и также испытываю соблазн еще раз попытаться написать более быструю хеш-таблицу.

Если вы действительно используете этот алгоритм в своем коде, дайте автору знать, насколько он подходит вам. Спасибо!