28.03.2022 11:46
IvanWiz 2 1600 Источник
Первая статья в серии "Методы выявления причинно-следственной связи в динамическом ценообразовании", продолжающая доклад "Causal Methods in Dynamic Pricing" (Ваня Горбань, Денис Пятых) ODS'21.
Первая статья в серии "Методы выявления причинно-следственной связи в динамическом ценообразовании", продолжающая доклад "Causal Methods in Dynamic Pricing" (Ваня Горбань, Денис Пятых) ODS'21.

Мы привыкли, что Machine Learning предоставляет нам большое количество предиктивных методов, которые с каждым годом предсказывают события лучше и лучше. Деревья, леса, бустинги, нейронные сети, обучение с подкреплением и другие алгоритмы машинного обучения позволяют предвидеть будущее все более отчетливо. Казалось бы, что нужно еще? Просто улучшать методы и тогда мы рано или поздно будем жить в будущем так же спокойно, как и в настоящем. Однако не все так просто.

Когда мы рассматриваем бизнес задачи, мы часто сталкиваемся с двумя моментами. Во-первых, мы хотим понять что к чему относится и что с чем связано. Нам важна интерпретация. Чем сложнее модели мы используем, тем более нелинейные они. Тем больше они похожи на черную коробку, в которой очень сложно выявить связи, понятные человеческому разуму. Все же мы привыкли мыслить довольно линейно или близко к тому. Во-вторых, мы хотим понять - если мы подергаем вот эту "ручку", изменится ли результат в будущем и насколько? То есть, мы хотим увидеть причинно-следственную связь между нашим целевым событием и некоторым фактором. Как сказал Рубин - без манипуляции нет причинно следственной связи. Мы часто ошибочно принимаем обыкновенную корреляцию за эту связь. В этой серии статей мы сконцентрируемся на причинах и следствиях.

Но что не так с привычными нам методами ML? Мы строим модель, а значит, предсказывая значение целевого события мы можем менять значение одного из факторов - одной из фич и тогда мы получим соответствующее изменение таргета. Вот нам и предсказание. Все не так просто. По конструкции, большинство ML методов отлично выявляют корреляцию между признаком и таргетом, но ничего не говорят о том, произошло ли изменение целевого события именно из-за изменения значения фичи. То есть, ничего не говорят нам о том - что здесь было причиной, а что следствием.

Чтобы прояснить о чем я, давайте посмотрим на задачу с другой стороны - чуть более формальной. Часто можно встретить следующую запись для модели машинного обучения:

\begin{equation}y = a(X)+\epsilon\end{equation}

Здесь y - наше целевое событие, a(X) - некоторый ML алгоритм, \epsilon- неустранимая ошибка. На самом деле a(X) в уравнении выше мы не знаем и часть просто предполагаем, что он именно такой, исходя из известных нам свойств целевого события и признакового пространства.

После "обучения" модели, мы получаем оценку алгоритма \hat{a}(X), с помощью которого получаем предсказания:

\begin{equation} \hat{y} = \hat{a}(X) \end{equation}

При этом, существует некоторая ошибка нашей оценки \hat{\epsilon} = y-\hat{y}, которую мы можем найти. Наш алгоритм строится с целью минимизации различных функций потерь от предсказания и фактического значения целевой переменной.

Вернемся к основному вопросу. Предположим, среди наших X присутствует некоторый признак, через который мы можем влиять на таргет, что мы очень хотим делать. Назовем его T. Оставшееся множество признаков обозначим

X\setminus T \equiv X_{\overline{T}}

Для того, чтобы это вписать в нашу формулу, предлагаю записать множество признаков следующим образом: X\equiv\left\{X_{\overline{T}}, T\right\}. Тогда наше предсказание выглядит:

\begin{equation} \hat{y} = \hat{a}(X_{\overline{T}}, T) \end{equation}

Под "воздействием" мы понимаем следующее: действительно ли, меняя T в реальности, я изменю y? Обозначим

\hat{y}_{\Delta T} = \hat{a}(X_{\overline{T}},T+\Delta T) \ \ и \ \ y_{\Delta T} = a(X_{\overline{T}},T+\Delta T).

Записывая строго (и предпологая определенный вид распределения ошибки и данных), мы хотим, чтобы следующее утверждение было верно:

\hat{y}\sim\mathcal{N}(y, \hat{\sigma}^2) \implies \hat{y}_{\Delta T} \sim \mathcal{N}(y_{\Delta T}, \hat{\sigma}^2)

То есть, мы хотим, чтобы изменив T мы получили результат и были уверены в нем также, как если бы он был изменен естественным образом. Однако, оказывается, что модели машинного обучения часто так не работают. Они находят корреляции, но это не значит, что изменив наше воздействие мы изменим результат.

Иллюстрацию этого удобно привести с помощью графа причинно-следственных связей. Подробности этого мы оставим за пределами этой статьи, но то, что я покажу будет понятно на интуитивном уровне. Предположим, наши данные описываются следующим образом:

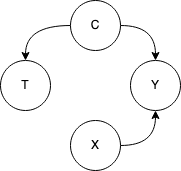
Здесь стандартно: Y - таргет, X - признаки объекта, T - наше воздействие. За C мы принимаем здесь так называемый Confounder - переменную, воздействующую на T и на Y. Если переменная C является не наблюдаемой для нас, то стандартная модель машинного обучения, глядя на корреляцию между изменениями T и Y сможет заметить эту связь. Однако, очевидно что изменяя T мы не изменим Y - для этого должна измениться C! Здесь мы увидели частный случай проблемы эндогенности - проблема упущенной переменной. Видно, что когда мы пытаемся не просто найти корреляции между переменными и прогнозировать изменения в таргете, исходя из наблюдений, а пытаемся влиять на таргет - все становится немного сложнее.

Давайте попробуем также посмотреть на проблемы причинно-следственной связи с точки зрения их отличий от проблем Machine Learning и Statistical Learning. Отличная иллюстрация приводится в книге Elements of Causal Inference: Foundations and Learning Algorithms (Peters et al., 2017):

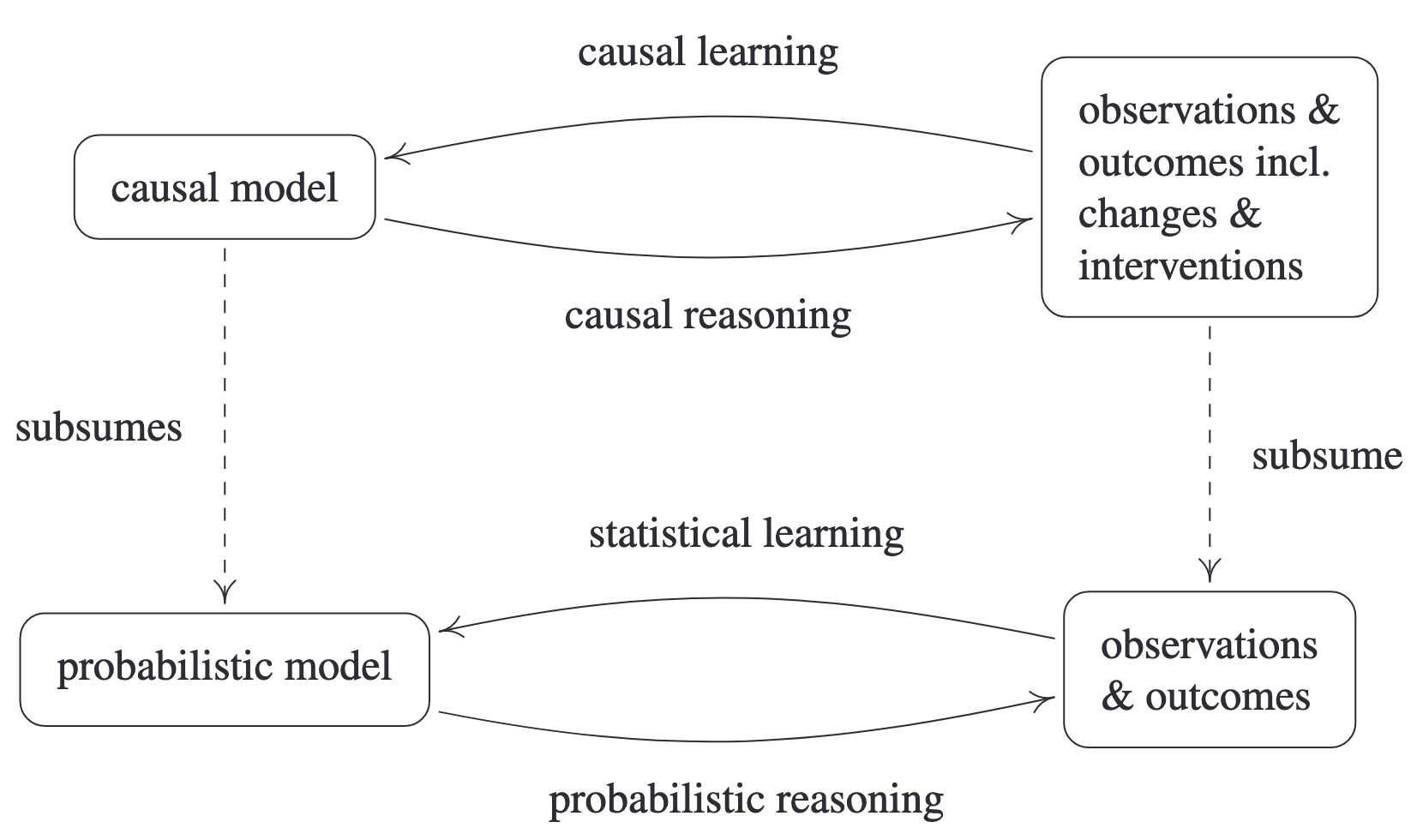
Типичные задачи эконометрики - statistical learning, машинного обучения - probabilistic reasoning и их связь с задачами causal learning - выявления причинно-следственных связей и causal reasoning - предсказания (управления) с учетом этих связей.
Типичные задачи эконометрики - statistical learning, машинного обучения - probabilistic reasoning и их связь с задачами causal learning - выявления причинно-следственных связей и causal reasoning - предсказания (управления) с учетом этих связей.

Ещё одна иллюстрация, которая помогает понять эволюцию мысли от корреляции к причинно-следственной связи (из книги The Book of Why: The New Science of Cause and Effect (Judea Pearl, Dana Mackenzie)):

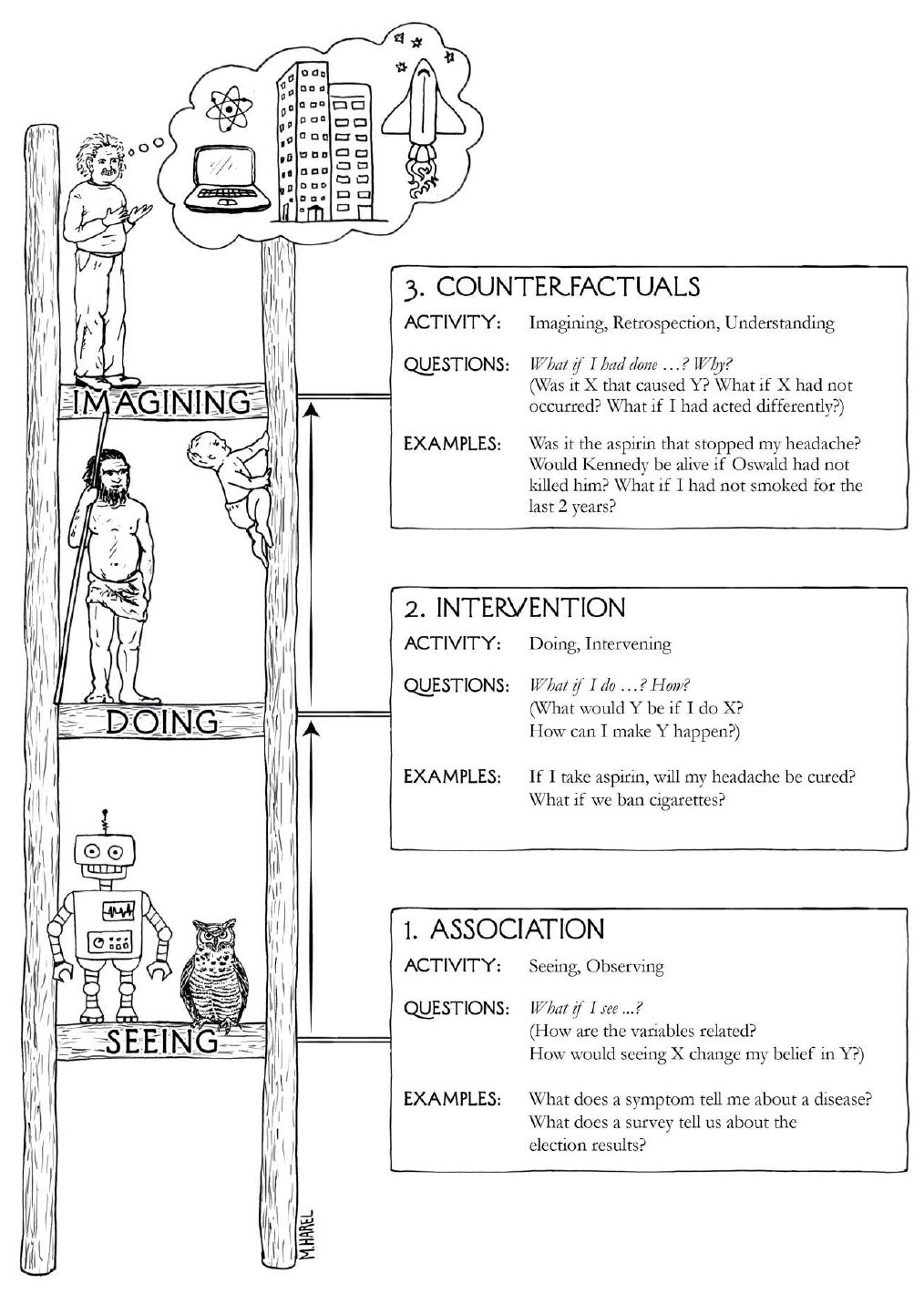
Иллюстрация Maayan Harel. Мысль эволюционирует от связи наблюдений с результатом в попытки изменить реальность с помощью доступных инструментов. Финальной ступенью является сослагательное наклонение и создание воображаемых миров для понимания реальных процессов и альтернативных исходов.
Иллюстрация Maayan Harel. Мысль эволюционирует от связи наблюдений с результатом в попытки изменить реальность с помощью доступных инструментов. Финальной ступенью является сослагательное наклонение и создание воображаемых миров для понимания реальных процессов и альтернативных исходов.

Но давайте вернемся к эндогенности. Следующий раздел для того, чтобы узнать или вспомнить что же это такое.

Эндогенность

Строго говоря, эндогенность - это корреляция объясняющей переменной (признака) с ошибкой. В математической записи это выглядит следующим образом:

\begin{align*}y = a(X)&+\epsilon\\ corr(x, \epsilon) \ne 0&, x\in X \end{align*}

Если говорить о предыдущем примере, то в нем как раз это и происходит, за счет того, что C\in\epsilon. Давайте посмотрим - какие еще бывают варианты эндогенности.

Принято выделять следующие проблемы:

  • Проблема упущенной переменной (omitted variable)

  • Обратная причинно-следственная связь (reverse causality)

  • Ошибка в измерениях (measurement error)

Все эти типы эндогенности отличаются присутствием корреляции ошибки и одного из признаков.

Выглядит очень теоретически. К чему это приводит на практике? Сейчас приготовьтесь испытать дежавю (особенно, если вы смотрели телевизор в последние несколько лет):

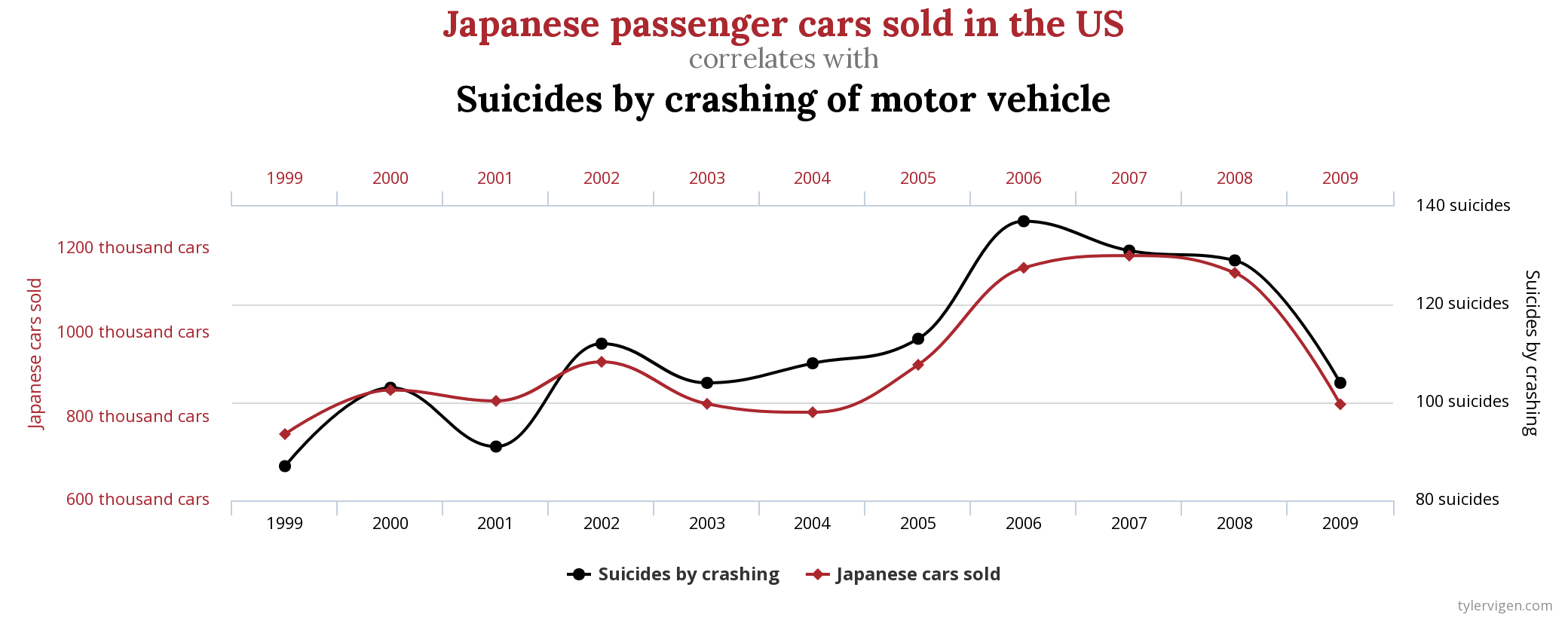
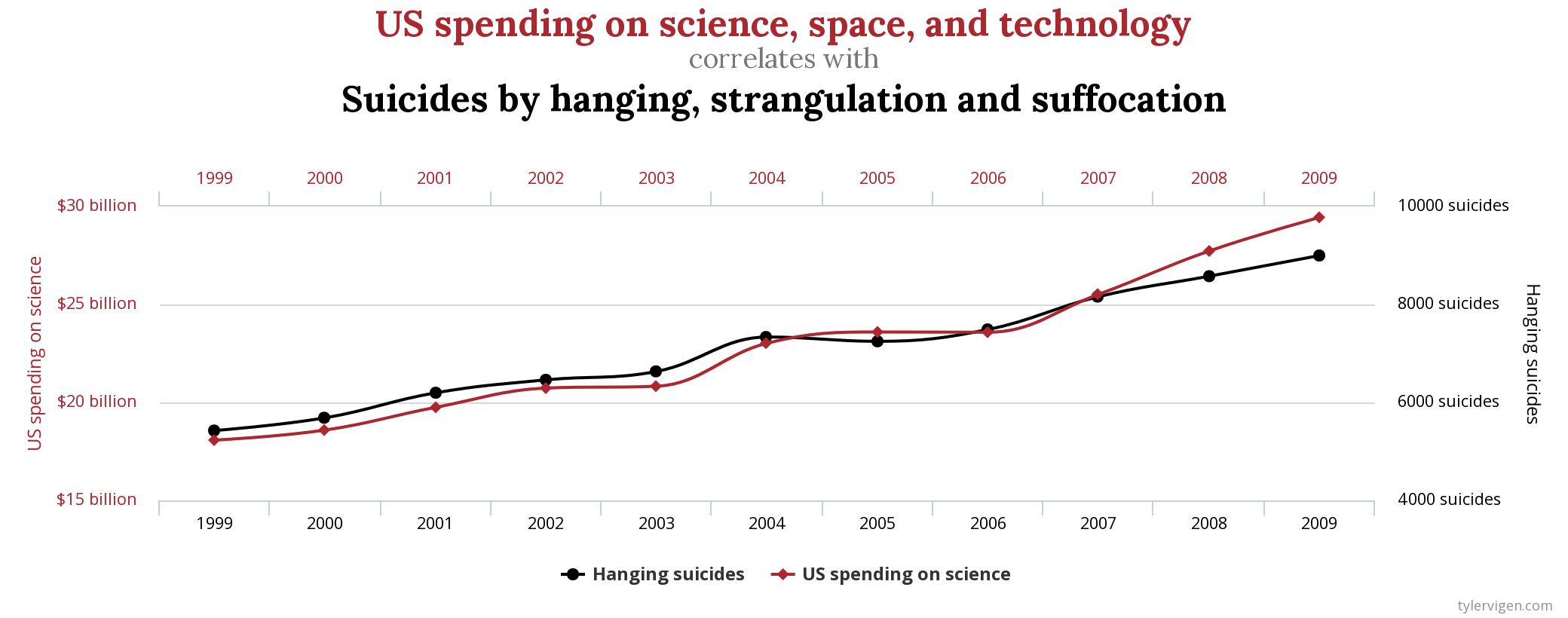
Иллюстрации взяты из источника: https://www.tylervigen.com/spurious-correlations. Первая и третья иллюстрация действительно могут быть названы "ложными", так как процесс, который объединяет их сложно формализуем и лежит глубоко, однако второй пример вполне может быть признаком активности автомобильного рынка и притока водителей-новичков на дороги. В целом, постаравшись, все эти процессы можно объяснить проблемой ommited variable (кроме разве что маргарина).
Иллюстрации взяты из источника: https://www.tylervigen.com/spurious-correlations. Первая и третья иллюстрация действительно могут быть названы "ложными", так как процесс, который объединяет их сложно формализуем и лежит глубоко, однако второй пример вполне может быть признаком активности автомобильного рынка и притока водителей-новичков на дороги. В целом, постаравшись, все эти процессы можно объяснить проблемой ommited variable (кроме разве что маргарина).

Поставим себя на место парламентария - законотворца, который к нашему всеобщему сожалению не освоил отличие корреляций от причинно-следственных связей. Дабы укрепить семейные связи в первом случае наш герой может принять решение запретить маргарин к примеру. Это будет логично. Во втором случае, для спасения жизней своих сограждан он, пожалуй, предложит наложить эмбарго на продажу японских автомобилей, что вызовет политическую напряженность, но главное, что благое дело сделано. И, наконец, он избавит граждан США от заразы науки и технологий, тем самым пытаясь значительно снизить смертность. Что ж, может быть и не стоит изучать причинно-следственные связи, в конце концов срок депутата ограничен.

Задача

Что ж, надеюсь, что вы как минимум порадовались, посмотрев на красивые картинки, теперь перейдем к задаче, которую мы излагали в докладе. Перед нами стояла проблема улучшения системы ценообразования для товаров (мобильной техники и аксессуаров) с целью повышения прибыли бизнеса с партии этих товаров. Давайте разберем эту формулировку по словам, чтобы понять - что же от нас хотят. Начнем с конца:

  • Партия товаров

    Я предлагаю рассматривать некоторый аксессуар. Например, некоторое универсальное зарядное устройство для смартфонов. Для простоты, пусть его технология не будет подвержена старению, хотя бы на горизонте года. Пусть его продажи несильно зависят от выхода новых моделей смартфонов. Партия (stock) это заранее известный объем закупки. Мы можем воспринимать её как набор зарядных устройств, который мы купили, скажем, в январе и следующая поставка будет через год.

  • Повышение прибыли

    Прибыль давайте также понимать довольно просто. Это наша выручка (цена, умноженная на количество проданного товара) минус наши издержки (стоимость закупки). Цену хранения единицы товара будем считать пренебрежимо малой. В конце концов, для зарядных устройств это очень близко к правде. Записывая формально:

    \pi= pq - c q

    Здесь \pi- прибыль, p - розничная цена, q - количество проданного товара, c-оптовая цена закупки товара.

  • Улучшение системы ценообразования Из предыдущего упрощенного уравнения не понятно - причем здесь цена? Максимум для \piздесь достигается за счет увеличения цены до бесконечности. Но на то она и упрощенная. Давайте сделаем её чуть реалистичней:

    \begin{equation}\pi(p) = pq(p) - cq(p)\end{equation}

    Здесь мы отразили немного больше зависимостей. Очевидно, объем проданного товара зависит от цены. При этом, чем выше цена, тем меньше объем продаж. При этом, закупка у нас фиксирована и мы имеем закупленную партию как факт, так что цена закупки - константа.

Казалось бы, давайте просто решим простейшую задачу оптимизации и выставим оптимальную цену. Но, все не так просто. Во-первых у нас целый год. Все, что не будет продано за год будет продаваться с большим дисконтом и приносить убыток, хранить это станет также дорого. Мы можем считать, что все, что не продано за год - выброшено.

Во-вторых, есть конкуренты и, повышая цену, мы теряем в продажах гораздо больше, чем было бы, будь мы монополистами. В-третьих, у нас может быть очень мало истории колебания цен, чтобы выявить зависимость q(p) при больших изменениях цены.

Начнем с казалось бы более простых задач и попробуем решить все проблемы, которые описали выше и некоторые другие.

Оптимальная цена

Начнем с выставления оптимальной в моменте цены. Как выставить эту цену?

На помощь здесь конечно придет простейшая теория оптимизации и основы микроэкономики. Решим задачу оптимизации, дабы найти оптимальную цену. Из FOC:

\begin{equation}p^*\dot{q}(p^*)+q(p^*)-c\dot{q}(p^*) = 0\end{equation}

$$ $$

И что мы видим? Нам позарез нужно понять зависимость q(p) для решения уравнения. Для начала мы решили оценить её с помощью простой модели линейной регрессии:

q = \alpha+\beta_1 p + {\beta_KX}+\epsilon

Здесь X - набор признаков, и, соответственно, коэффициентов при нем тоже несколько, надеюсь, никого не запутает такая нотация. \epsilon предполагаем i.i.d (это очень сильное предположение, особенно учитывая автокорреляцию ошибок, если мы смотрим во времени, но, чтобы не размывать целей примера, здесь я не буду углубляться в решение этой задачи).

В результате решения этой задачи мы можем получить некую оценку \hat{\beta}_1, которая показывает нам каким образом количество продаж товара зависит от цены. Звучит это просто, но на деле конечно нас ждут не дождутся проблемы:

  • На каждый товар не так много наблюдений, потому есть большой риск не увидеть статистической значимости в нашем коэффициенте

  • Есть товары, цена которых исторически не менялась, а значит наша модель не сработает для них в целом (нарушены базовые предположения OLS)

  • Есть товары, для которых мы видим положительную оценку \hat{\beta}_1(как бы вы интерпретировали её?)

Так как мы являемся последователями стоической философии, то мы представляли даже худшие варианты развития событий - такие как столкновение с метеоритом или чума, так что то, что мы увидели нас даже обрадовало. Какие идеи у нас возникли для решения этих задач?

Число наблюдений

Очевидным способом борьбы с этой бедой кажется объединение товаров в одну выборку. Но каким образом различать их? Предположим, что зависимости не универсальны и не отличаются от товара к товару. Первой попыткой может быть добавить dummy переменные (или fixed effects) на различные товары. Но тогда мы добавим огромное число переменных и выигрыш от объединения будет крайне невелик.

Есть другой вариант - в рамках одного класса товаров, давайте опишем их некоторыми признаками, присутствие которых обусловленно классом товара, а их значения могут отличаться от одного товара к другому. Например, если это зарядные устройства, то они могут различаться типом, производителем, мощностью. Таким образом мы, вводя некоторые вполне валидные предположения, выиграем от роста количества наблюдений.

Отсутствие изменения цены

Здесь мы можем пойти двумя путями. Первый уже произошел автоматически. В результате перехода от индивидуальных товаров к их группе, мы уже добавили вариацию в цену (предполагая единую зависимость от цены для всей группы). Второй путь - рандомизация. Для тех товаров, которые не имели исторических изменений в цене, мы можем волевым усилием устроить случайные изменения цены в разумных пределах.

Положительная корреляция цены и продаж

Эта проблема интересна, особенно в контексте нашей прошлой дискуссии о причинно-следственной связи и проблеме эндогенности. Давайте подумаем - может ли быть такое, что повышая цену мы начинаем продавать больше товара? Вполне возможно, но рост продаж вряд ли будет объясняться ростом цены, особенно в контексте наших товаров. Переводя на графический язык, положительный коэффициент говорит нам о следующей зависимости между ценой и продажами:

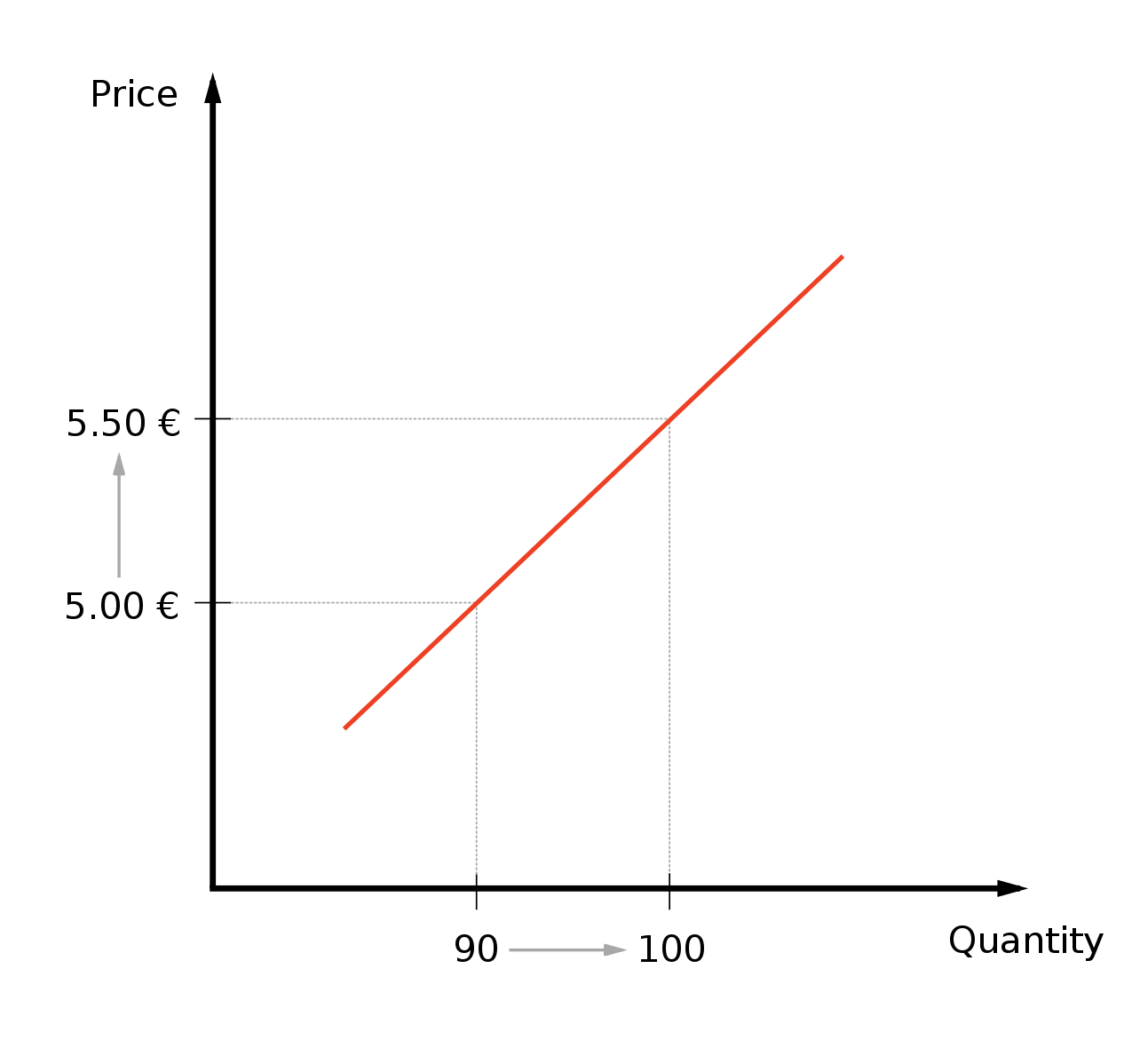
Думаю этот график довольно наглядно показывает, что как бы нам ни хотелось ничего не делать с этим коэффициентом - не выйдет. Маловероятно, что повышая цену мы добьемся этим увеличения продаж. В противном случае, нам стоило бы поставить цену на данное зарядное устройство равной бесконечности и перепрофилировать бизнес.

И снова эндогенность

Мы задумались. То ли половина наших товаров “неправильные”, то ли здесь где-то зарыта какая-то другая собака ???? . Тут мы вспоминаем про проблемы эндогенности, которые мы недавно разбирали в теории и думаем - возможно ли что где-то здесь мы столкнулись с одной из них? Вполне. Давайте посмотрим что это могло быть. Огласим весь список снова:

  1. Упущенная переменная

  2. Обратно причинно-следственная связь

  3. Ошибка измерений

Предположим, что третье мы можем исключить. Мы верим нашим данным - там все хорошо и нет систематически искажающей результаты ошибки. Что насчет остальных?

Упущенная переменная. Вполне может быть. Что если мы в рамках года взяли только осень и забыли включить сезонную компоненту в анализ? Мы увидим повышение цен на товары (которое мы проводили) и повышение спроса. Более того, здесь мы чувствуем сразу присутствие и второй проблемы - мы повысили цену зная, что будет повышение спроса, а значит, повысятся продажи, а значит мы можем безболезненно поднять цену, чтобы подогнать оптимальную под возросший спрос. Вот вам и обратная причинно-следственная связь.

Еще? Давайте подумаем. Конкуренты. Что если в момент повышения наших цен - конкуренты подняли цены ещё больше. Все покупатели конечно расстроились, что такое вот происходит, но пришли к нам, так как у нас стало дешевле. Тогда можно сказать, что цены конкурентов являются упущенной переменной. Включив её, мы скорректируем нашу ошибку, наш bias.

Можно продолжить. Но зачем? Эти упражнения полезны и интересны для кого-то, но помогают ли они нам решить проблему на практике? Как получить адекватную и близкую к реальной зависимость спроса от предложения? Очень просто. Omitted variable, которую мы можем таки отыскать, мы можем просто включить в регрессионную модель, тем самым скорректировав отклонение. Однако кто гарантирует, что мы не забыли что-нибудь? Кто гарантирует, что мы включили все упущенные переменные, а тем более - кто гарантирует, что мы не забыли где-нибудь обратную причинно следственную связь? Что с ней делать?

Здесь нам на помощь приходят инструментальные переменные.

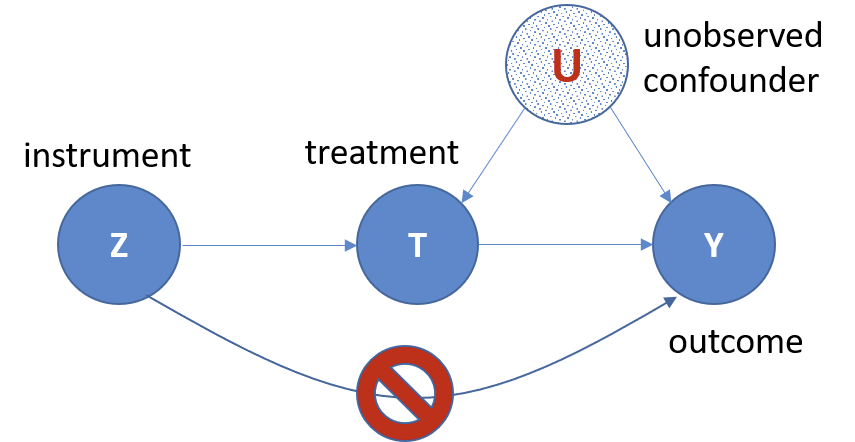
https://www.microsoft.com/en-us/research/blog/adversarial-machine-learning-and-instrumental-variables-for-flexible-causal-modeling/
https://www.microsoft.com/en-us/research/blog/adversarial-machine-learning-and-instrumental-variables-for-flexible-causal-modeling/

Стандартно инструментальные переменные обозначаются как Z. На картинке выше видно, что инструментальная переменная должна быть подобрана так, чтобы воздействовать на итоговую зависимую переменную только через treatment переменную, которую мы хотим избавить от эндогенности (в случае на картинке - от unobserved confounder).

Давайте посмотрим как выглядит наша проблема в более строгой формулировке.

E[\hat{\beta}] = E[(X^TX)^{-1}(X^TY)] = E[(X^TX)^{-1}(X^T(X\beta+\epsilon))]\\ = E[\beta+X^T\epsilon] = \beta + E[X^T\epsilon]

Второе слагаемое и есть bias, который мы получаем за счет эндогенности. Если существует переменная, коррелирующая с Y и X, соответственно

exist\ \ x: E[x\epsilon]\ne 0

Классический пример использования инструментальной переменной - 2-stage least squares (2SLS) оценка. Название может подсказать нам, что этот метод имеет нечто общее с OLS (ordinary least squares) или МНК оценкой.

Шаги здесь следующие и довольно простые. Пусть у нас есть парочка инструментальных переменных z_1 \ и \space z_2. Также есть наша переменная x_k,являющаяся эндогенной (в нашем примере - это цена). Тогда два этапа выглядят так:

  1. Оценить OLS:

    x_k \sim x_{\overline{k}},z_1, z_2,

    где x_{\overline{k}}- экзогенные иксы x_{\overline{k}} = \{1, x_1, \dots, x_{k-1}\}, а z_1, z_2- инструментальные переменные для x_k. В итоге получим некоторую \hat{x}_k.

  2. Наша оценка получается из подстановки результата предыдущего этапа вместо x_kТак как \hat{x}_kэкзогенная по определению, то при выполнении некоторых предположений несмещенной оценкой \beta_{k}является \hat{\beta}_{k_z}:

    \hat{y} = \hat{\beta} x_{\overline{k}}+\hat\beta_{k_z}\hat{x}_k

Мы здесь опустили некоторые предположения касательно инструментов, но это все же статья не только об инструментальных переменных и не такая техническая, как это возможно, поэтому интересующихся отсылаю к наилучшему источнику по теме: J.M. Wooldridge, Econometric Analysis of Cross Section and Panel Data, Chapter 5.

А не слабовато?

Вкратце - все конечно зависит от инструментов, но в целом, часто мы получаем достаточно маломощные оценки интересующего нас эффекта. В случае нашей задачи - оценки эластичности цены. Чем мощнее эта оценка, тем точнее мы можем оптимизировать цену и тем меньше изначальная выборка нам требуется для этой оптимизации.

Method of Direct Estimation

Данный метод был представлен в статье M. Ratkovic, D. Tingley, Causal Inference Through the Method of Direct Estimation. Он позволяет проводить оценку причинно-следственных связей, фокусируясь на мгновенном причинно-следственном эффекте (instantaneous causal effect), который иначе можно рассматривать как причинно-следственный эффект на уровне одного наблюдения. В своей статье Ratkovic and Tingley строят регрессию с высокой степенью нелинейности между ковариатами и treatment переменной (это например наша цена), которую затем используют для предсказания альтернативных исходов (counterfactuals). Другими словами, они строят регрессию, а затем, подставляя другие значения treatment переменной пытаются понять что с этим наблюдением было б если бы все было иначе.

Пока это выглядит немного смазанно. Давайте посмотрим подробнее на алгоритм, думаю станет понятней.

Пусть наша цена - treatment и обозначим её за T. Также, спрос (который у нас является таргетом) обозначим за Y(T). Причинно-следственный эффект изменения цены на спрос можно тогда обозначить за

\Delta_i(Y''_i,Y'_i) = Y_i(T''_i)-Y_i(T_i'),

здесь T'=T, a T''=T+\delta, где дельта - небольшое изменение нашей цены. В пределе мы хотим оценить частную производную:

lim_{\delta \rightarrow0}\nabla_{T_i}(\delta) = lim_{\delta \rightarrow0}\frac{\mathbb{E}\{Y_i(T_i+\delta)-Y_i(T_i)|X_i\}}{\delta}

Здесь видно, что если мы оценим \mathbb{E}\{Y_i(T_i)|X)линейной моделью, то получим просто коэффициент при эффекте воздействия. Однако мы не хотим делать предположения о линейной зависимости и добавляем нелинейные взаимодействия тритмента и переменных. В статье предлагается вид:

Y_i=\mu_Y+R^o(T_i,X_i)^Tc^o+\epsilon_i

c^o- параметры модели, R^o(T_i, X_i)^T- B-spline базис. Далее предлагается отфильтровать нелинейные компоненты при помощи L1 регуляризатора. Полученное подмножество называем R_{TX}(T_i, X_i). В дальнейшем после оценки параметров регрессии мы получаем искомый предел как:

lim_{\delta \rightarrow0}\hat{\nabla}{T_i}(\delta) = lim_{\delta \rightarrow0}\frac{R_{TX}(T_i+\delta, X_i)-R_{TX}(T_i, X_i)}{\delta}\hat{c}_{TX}

Казалось бы, все просто. Однако здесь нигде не учитывается эндогенность. Как мы оценим то же самое, если включим инструментальные переменные?

В статье предлагается аналог 2SLS оценки, называемый LICE (Local Instantaneous Causal Effect). Во-первых, оценивается так называемый instantaneous encouragement - эффект от небольшого изменения инструмента на одном наблюдении. Он показывает эффект от изменения инструмента на тритмент (переменную воздействия):

\nabla_{Z_i}^{IV}(\delta) = \mathbb{E}(T_i(Z_i+\delta) - T_i(Z_i)|X_i)

Вторая часть оценки LICE - instantaneous intent to treat on the treated - показывает эффект от изменения инструмента на целевую переменную:

\nabla_{T_i}^{IV}(\delta) = \mathbb{E}\{Y_i(T_i(Z_i)+\nabla_{Z_i}^{IV}(\delta))-Y_i(T_i(Z_i))|X_i\}

Итак, в итоге:

LICE =lim_{\delta \rightarrow0}\nabla^{IV}{T_i, Z_i}(\delta)= lim_{\delta \rightarrow0}\frac{\nabla^{IV}{T_i}(\delta)}{\nabla^{IV}{Z_i}(\delta)}

Можно показать, что:

LICE =lim_{\delta \rightarrow0}\nabla^{IV}_{T_i, Z_i}(\delta)=\hat{\theta}^{TSLS} = \frac{Cov(Y_i,Z_i|X_i)}{Cov(T_i,Z_i|X_i)}

Отсюда видно, что для фиксированных параметров наблюдения мы можем предсказать эффект от воздействия на него, имея наше воздействие T и инструментальную переменную Z.

ML модификация MDE

Мы не удовлетворились имеющимися моделями линейной регрессии и решили обобщить метод на работу с произвольным алгоритмом следующим образом. Давайте для начала посмотрим как выглядят модели линейной регрессии в статье:

Y_i=\mu_Y+R_1(T_i, X_i)^Tc_1+R_2(X_i)^Tc_2+\epsilon_i^Y\\T_i=\mu_Y+R_3(Z_i, X_i)^Tc_3+R_4(X_i)^Tc_4+\epsilon_i^T

Заменим линейную регрессию на произвольный алгоритм:

Y_i=a_1(T_i,X_i)+\epsilon_i^Y\\T_i=a_2(Z_i,X_i)+\epsilon_i^T

В качестве алгоритмов мы выбрали модели случайного леса. И конечно это лишь звучит просто, в дальнейшем возникло много особенностей ввиду того, что в общем случае решение, выдаваемое лесом не является гладким, так что нам пришлось аппроксимировать его гладкой функцией. Но об этом в другой раз.

Во второй части этой статьи вы узнаете как мы в итоге решили проблему негладкости решения, а также как реализовали систему динамической оптимизации цены. Надеюсь эта статья была вам полезна, ну или хотя бы расширила ваш кругозор. Спасибо!

Комментарии (2)


  1. MentalBlood
    28.03.2022 12:32
    #24208623

    Поставим себя на место парламентария — законотворца, который к нашему всеобщему сожалению не освоил отличие корреляций от причинно-следственных связей. Дабы укрепить семейные связи в первом случае наш герой может принять решение запретить маргарин к примеру. Это будет логично. Во втором случае, для спасения жизней своих сограждан он, пожалуй, предложит наложить эмбарго на продажу японских автомобилей, что вызовет политическую напряженность, но главное, что благое дело сделано. И, наконец, он избавит граждан США от заразы науки и технологий, тем самым пытаясь значительно снизить смертность

    Ну подождите, он же просто учитывает только одну корреляцию, забывая про другие


    Похоже, что каузальность это сжатая и ультиматизированная форма множества корреляций. Ну действительно, наша уверенность в истинности определенных причинно-следственных связей основана на стабильности корреляций, соответствующих им


  1. Oz_Alex
    28.03.2022 14:39
    #24209301

    Как Мегафон может объяснить семь лет попыток списать у меня деньги со счёта, когда мой телефон с мегафоновской симкой просто лежит на столе в Австралии, изредка принимает смс для логина в госуслуги и просто заряжается без каких-либо действий с моей стороны?
    На счету с первой попытки списания хрен пойми за что больше 300 рублей не было ни разу.

    Скриншот смс