На прошлом уроке мы изучили некоторые способы поиска областей интереса на изображении. Напомню, что мы делали:

• пытались найти по цвету (чаще всего так делать не надо);

• пытались найти круглый знак посредством функции HoughCircles (иногда работает);

• а еще мы изучили морфологические операции (открытие закрытие).

Сегодняшний урок будет более глубоко посвящен работе с контурами, так как часто контур помогает выдели фичи на изображения, а так же области интересов (благодаря контуру, мы можем охватить форму объекта).

Для начала вспомним, как находить контуры:

import cv2
import numpy as np

my_photo = cv2.imread('DSCN1311.JPG')
filterd_image  = cv2.medianBlur(my_photo,7)
img_grey = cv2.cvtColor(filterd_image,cv2.COLOR_BGR2GRAY)

#set a thresh
thresh = 100

#get threshold image
ret,thresh_img = cv2.threshold(img_grey, thresh, 255, cv2.THRESH_BINARY)

#find contours
contours, hierarchy = cv2.findContours(thresh_img, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)

#create an empty image for contours
img_contours = np.uint8(np.zeros((my_photo.shape[0],my_photo.shape[1])))

cv2.drawContours(img_contours, contours, -1, (255,255,255), 1)

cv2.imshow('origin', my_photo) # выводим итоговое изображение в окно
cv2.imshow('res', img_contours) # выводим итоговое изображение в окно

cv2.waitKey()
cv2.destroyAllWindows()

Обратите внимание, что перед выделением контуров мы используем фильтрацию. Вот что у нас получилось:

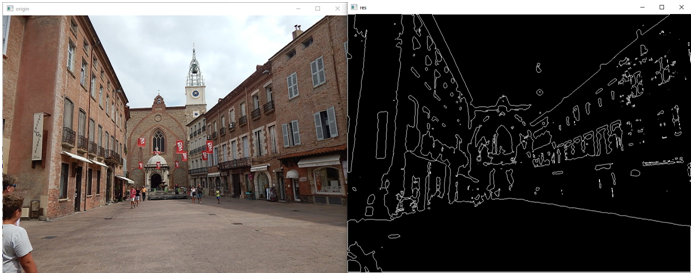
Без фильтрации у нас бы получилось вот что (для сравнения, справа без фильтра, слева с фильтром):

Теперь посмотрим, а что именно у нас возвращает findContours и как с этим работать:

contours, hierarchy = cv2.findContours(thresh_img, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
print(type(contours),type(hierarchy))

Мы получили вывод:

<class 'tuple'> <class 'numpy.ndarray'>

Таким образом, сам контур – это обыкновенный тьюпл, а второе возвращенное значение массив numpy. Если мы посмотрим этот тьюпл отладчиком, то увидим, что элементами этого тьюпла являются массив numpy:

Иными словами, функция возвращает целое множество контуров. По идее, можно работать с каждым из контуров по отдельности. Давайте, например, выведем на экран четвертый (он на самом деле будет под номером 3, считаем же с нуля) контур:

img_contours = np.uint8(np.zeros((my_photo.shape[3],my_photo.shape[1])))

Вот что мы увидим на картинке:

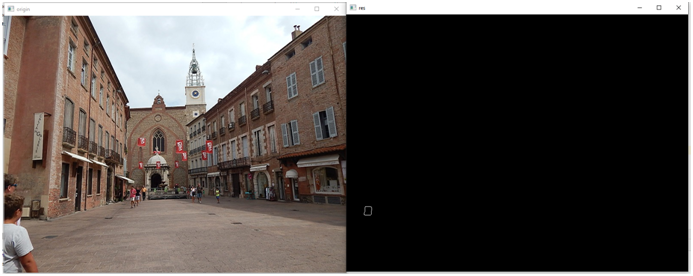
Можно вывести сразу несколько контуров:

sel_countours=[]
sel_countours.append(contours[3])
sel_countours.append(contours[7])
sel_countours.append(contours[8])
cv2.drawContours(img_contours, sel_countours, -1, (255,255,255), 1)

Вот что мы увидим:

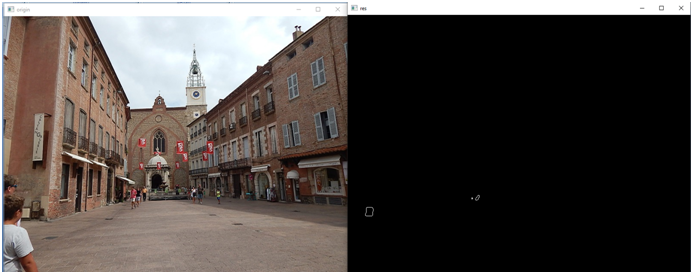
Найдем самый большой контур:

max=0
sel_countour=None
for countour in contours:
    if countour.shape[0]>max:
        sel_countour=countour
        max=countour.shape[0]

cv2.drawContours(img_contours, [sel_countour], -1, (255,255,255), 1)

Смотрим:

Надо сказать, что контур может храниться как в виде точек, так и в виде отрезков, в зависимости от установлено параметра аппроксимации:

contours, hierarchy = cv2.findContours(thresh_img, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)

В нашем случае установлен Simple, значит, контур храниться в виде отрезков, если мы нарисуем по точкам, то контура не получиться:

for point in sel_countour:
    y=int(point[0][1])
    x=int(point[0][0])
    img_contours[y,x]=255

Смотрим:

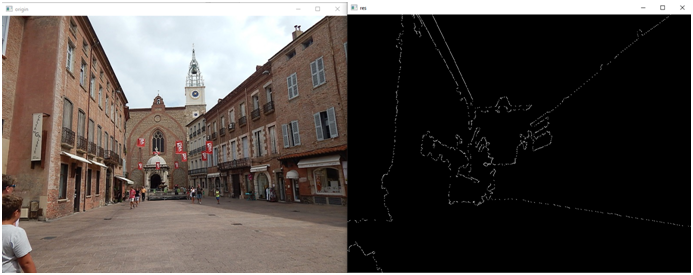
Но если вы укажете функции findContours что надо искать контуры без аппроксимации:

contours, hierarchy = cv2.findContours(thresh_img, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)

То контур будет как на предыдущей картинке.

С другой стороны, если у вас аппроксимация включена, то вы можете нарисовать контур, соединив точки линиями:

last_point=None
for point in sel_countour:
    curr_point=point[0]
    if not(last_point is None):
        x1=int(last_point[0])
        y1=int(last_point[1])
        x2=int(curr_point[0])
        y2=int(curr_point[1])
        cv2.line(img_contours, (x1, y1), (x2, y2), 255, thickness=1)
    last_point=curr_point

Получится то же самое, что и на первой картинке.

И так, функция findContours возвращает сгруппированные наборы точек, которые являются точками контура (или концами отрезков контура, в зависимости от типа аппроксимации).

Полученный контур мы можем и далее аппроксимировать:

import cv2
import numpy as np
import os
img = cv2.imread("DSCN1311.JPG")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
thresh = 100

#get threshold image
ret,thresh_img = cv2.threshold(gray, thresh, 255, cv2.THRESH_BINARY)

# find contours without approx
contours,_ = cv2.findContours(thresh_img,cv2.RETR_TREE,cv2.CHAIN_APPROX_NONE)

max=0
sel_countour=None
for countour in contours:
    if countour.shape[0]>max:
        sel_countour=countour
        max=countour.shape[0]

# calc arclentgh
arclen = cv2.arcLength(sel_countour, True)

# do approx
eps = 0.0005
epsilon = arclen * eps
approx = cv2.approxPolyDP(sel_countour, epsilon, True)

# draw the result
canvas = img.copy()
for pt in approx:
    cv2.circle(canvas, (pt[0][0], pt[0][1]), 7, (0,255,0), -1)

cv2.drawContours(canvas, [approx], -1, (0,0,255), 2, cv2.LINE_AA)

img_contours = np.uint8(np.zeros((img.shape[0],img.shape[1])))
cv2.drawContours(img_contours, [approx], -1, (255,255,255), 1)


cv2.imshow('origin', canvas) # выводим итоговое изображение в окно
cv2.imshow('res', img_contours) # выводим итоговое изображение в окно

cv2.waitKey()
cv2.destroyAllWindows()

Давайте посмотрим, что получиться:

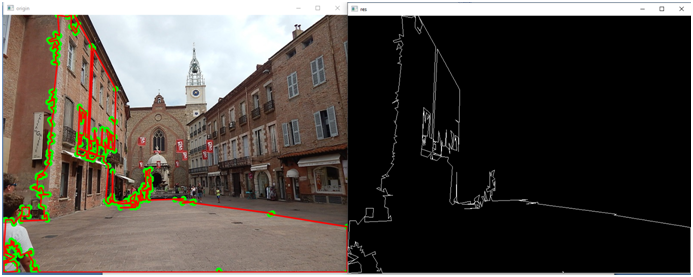
Мы можем управлять точность аппроксимации, меняя значение переменной eps. Поставим, например, вместо 0.0005 значение 0.005 и картинка будет уже совсем другой:

А теперь более внимательно рассмотрим кусок кода, ответственный за аппроксимацию:

# calc arclentgh
arclen = cv2.arcLength(sel_countour, True)

# do approx
eps = 0.0005
epsilon = arclen * eps
approx = cv2.approxPolyDP(sel_countour, epsilon, True)

Функция arcLength возвращает длину дуги контура. Давайте попробуем посмотреть длины разных контуров.  Только давайте сначала отсортируем контуры в порядке уменьшения их длин. Для этого определим кастмную сортировочную функцию:

def custom_sort(countour):
    return -countour.shape[0]

Теперь мы можем отсортировать контуры:

contours=list(contours)
contours.sort(key=custom_sort)

Самый длинный контур будет первым:

sel_countour=contours[0]

# calc arclentgh
arclen = cv2.arcLength(sel_countour, True)
print(arclen)

Остальные контуры будут поменьше, например, вот контур под индексом 5:

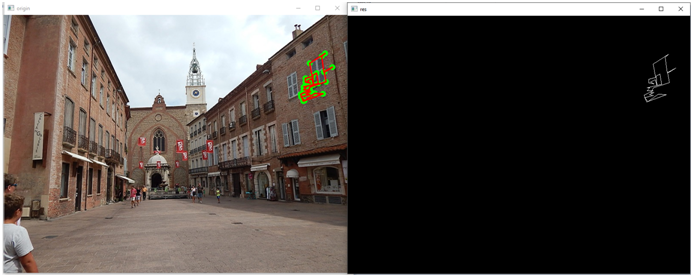
Идем дальше. Получив длину дуги контура, мы вычисляем так называемый эпсилон – параметр, характеризующий точность аппроксимации. В качестве критерия используется максимальное расстояние между исходной кривой и ее аппроксимацией.

Аппроксимируемый контур – это, по сути те же точки, соединенные отрезками, так что его можно вывести и так:

last_point=None
for point in approx:
    curr_point=point[0]
    if not(last_point is None):
        x1=int(last_point[0])
        y1=int(last_point[1])
        x2=int(curr_point[0])
        y2=int(curr_point[1])
        cv2.line(img_contours, (x1, y1), (x2, y2), 255, thickness=1)
    last_point=curr_point

И так, теперь мы знаем, что представляет собой полученный контур – это отрезки. Мы можем даже аппроксимировать эти отрезки, получив более грубый контур, избавиться тем самым от мелких деталей. Но что делать дальше? Как я уже писал в части 4, контур можно превратить в граф или в геометрические примитивы, тем самым описав его инвариантно к смещению, повороту и даже масштабированию.

Сейчас мы попробуем создать такое инвариантное описание объекта. Пусть это будет обыкновенная шариковая ручка:

Логично предположить, что надо работать с самым длинным контуром. Найдем, его, это мы уже умеем:

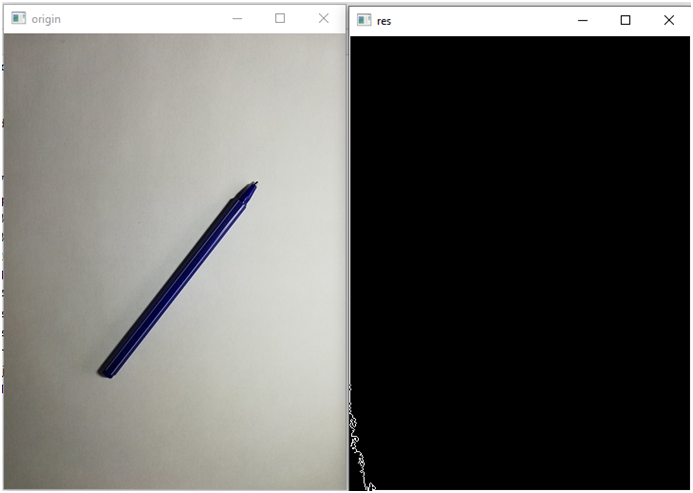
Нет, не угадали, придется перебирать. К счастью, контур оказался второй по длине:

contours,_ = cv2.findContours(thresh_img,cv2.RETR_TREE,cv2.CHAIN_APPROX_NONE)
contours=list(contours)
contours.sort(key=custom_sort)
sel_countour=contours[1]

Аппроксимируем его:

Как оказалось, при значении eps=0.005 контур имеет всего 7 элементов:

eps = 0.005
epsilon = arclen * eps
approx = cv2.approxPolyDP(sel_countour, epsilon, True)
print(len(approx))

Посмотрим, как будет выделен контур в других положениях:

В последнем случае мы получили, кстати, не 7, а 9 элементов. Короче, тут засада с тенью. В общем, надо как-то избавиться от мелких деталей. Но как? Поднять порог аппроксимации? Давайте сделаем 0.01:

Количество элементов стало 6. На других фотографиях, тоже кстати 6. Такой вот шестиугольник:

Теперь попробуем описать данный контур инвариантно. Можно сделать это двумя способами:

- углы между гранями контура;

- отношении длин сторон.

Оба способа будут инвариантны к смещению, повороту и масштабированию. Но вопрос: а с какой стороны считать? Один из вариантов, это найти центр контура и за начало взять самую удаленную от него точку. Как найти центр? Как среднюю координату всех точек контура.

sum_x=0.0
sum_y=0.0
for point in approx:
    x = float(point[0][0])
    y = float(point[0][1])
    sum_x+=x
    sum_y+=y
xc=sum_x/float(len((approx)))
yc=sum_y/float(len((approx)))

Отобразим центр после вывода контура:

cv2.circle(img_contours, (int(xc), int(yc)), 7, (255,255,255), 2)

Найдем точку, наиболее удаленную от центра:

max=0
beg_point=-1
for i in range(0,len(approx)):
    point=approx[i]
    x = float(point[0][0])
    y = float(point[0][1])
    dx=x-xc
    dy=y-yc
    r=math.sqrt(dx*dx+dy*dy)
    if r>max:
        max=r
        beg_point=i

Отрисуем ее:

point=approx[beg_point]
x = float(point[0][0])
y = float(point[0][1])
cv2.circle(img_contours, (int(x), int(y)), 7, (255,255,255), 2)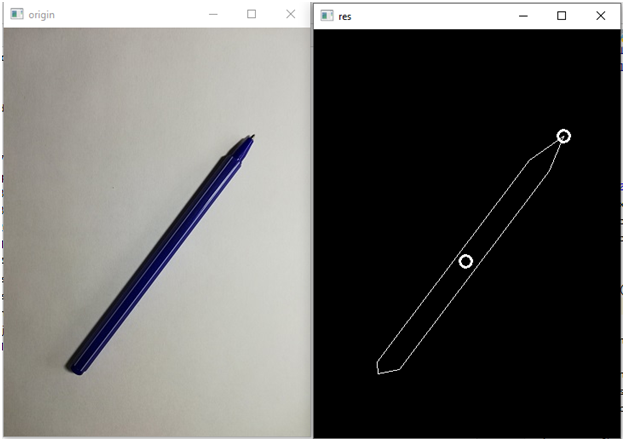

Теперь просто обойдем контур по часовой стрелке, начиная с найденной точки. Для этого преобразуем координаты точек в полярные и отсортируем их по углу.

Полярные координаты вычислим вот такой вот функцией:

def get_polar_coordinates(x0,y0,x,y,xc,yc):
    #Первая координата в полярных координатах - радиус
    dx=xc-x
    dy=yc-y
    r=math.sqrt(dx*dx+dy*dy)

    #Вторая координата в полярных координатах - узел, вычислим относительно начальной точки
    dx0=xc-x0
    dy0=yc-y0
    r0 = math.sqrt(dx0 * dx0 + dy0 * dy0)
    scal_mul=dx0*dx+dy0*dy
    cos_angle=scal_mul/r/r0
    sgn=dx0*dy-dx*dy0 #опредедляем, в какую сторону повернут вектор
    angle=math.acos(cos_angle)
    if sgn<0:
        angle=2*math.pi-angle
    return angle,r

Здесь мы задаем точку начала отчета, искомую точку и наш центр. Первая координата, это радиус, его мы вычислим по теореме Пифагора. Угол найдем через скалярное произведение. Тут, правда, есть засада. Через скалярное произведение мы вычислим угол между векторами, но не направление. Чтобы его вычислить, нам надо найти определить матрицы векторов. Знак это и будет направление вращения. Но нам надо не просто отрицательный угол, иначе при сортировке первая точка будет не начало отчета, а точка с самым отрицательным углом. Поэтому если направление в другую сторону, то вычтем этот угол из угла 2 пи радиан (360 градусов).

Если не понятно, то я сейчас наглядно продемонстрирую проблему. Но, давайте сначала отсортируем:

polar_coordinates=[]
x0=approx[beg_point][0][0]
y0=approx[beg_point][0][1]
print(x0,y0)
for point in approx:
    x = int(point[0][0])
    y = int(point[0][1])
    angle,r=get_polar_coordinates(x0,y0,x,y,xc,yc)
    polar_coordinates.append(((angle,r),(x,y)))
print(polar_coordinates)
polar_coordinates.sort(key=polar_sort)

А потом нарисуем:

img_contours = np.uint8(np.zeros((img.shape[0],img.shape[1])))
size=len(polar_coordinates)
for i in range(1,size):
    _ , point1=polar_coordinates[i-1]
    _, point2 = polar_coordinates[i]
    x1,y1=point1
    x2,y2=point2
    cv2.line(img_contours, (x1, y1), (x2, y2), 255, thickness=i)
_ , point1=polar_coordinates[size-1]
_, point2 = polar_coordinates[0]
x1,y1=point1
x2,y2=point2
cv2.line(img_contours, (x1, y1), (x2, y2), 255, thickness=size)

Смотрим, что получилось:

Для того, чтобы увидеть обход, я первые линии сделал тонкими, но по мере обхода они становятся толще.

А теперь уберем из функции перевода в полярные координаты наши манипуляции с определением направления вращения:

def get_polar_coordinates(x0,y0,x,y,xc,yc):
    #Первая координата в полярных координатах - радиус
    dx=xc-x
    dy=yc-y
    r=math.sqrt(dx*dx+dy*dy)

    #Вторая координата в полярных координатах - узел, вычислим относительно начальной точки
    dx0=xc-x0
    dy0=yc-y0
    r0 = math.sqrt(dx0 * dx0 + dy0 * dy0)
    scal_mul=dx0*dx+dy0*dy
    cos_angle=scal_mul/r/r0
    #sgn=dx0*dy-dx*dy0 #опредедляем, в какую сторону повернут вектор
    angle=math.acos(cos_angle)
    #if sgn<0:
    #    angle=2*math.pi-angle
    return angle,r

И вот тогда какая ерунда получится:

Так что, вернем что закоментили на место и продолжим.

Приступим к инвариантному описанию. Углы между гранями контура. Здесь мы будем исходить из того, что углы положительны и меньше 180 градусов, то есть не будем делать тех манипуляций с определением направление. Хотя… лучше даже определить не углы а косинусы углов, они примут значения от 0 до 1. По сути, это уже будет обычный вектор, который мы можем подать на вход какого-нибудь алгоритма классификации, например, нейросеть.

И так, функция вычисления косинуса угла между гранями (!!!!!!!):

def get_cos_edges(edges):
    dx1, dy1, dx2, dy2=edges
    r1 = math.sqrt(dx1 * dx1 + dy1 * dy1)
    r2 = math.sqrt(dx2 * dx2 + dy2 * dy2)
    return (dx1*dx2+dy1*dy2)/r1/r2

Обратите внимание, что в функцию мы задаем относительные координаты, а не абсолютные. И их нам надо вычислить, для этого напишем еще одну функцию:

def get_coords(item1, item2, item3):
    _, point1 = item1
    _, point2 = item2
    _, point3 = item3
    x1, y1 = point1
    x2, y2 = point2
    x3, y3 = point3
    dx1=x1-x2
    dy1=y1-y2
    dx2=x3-x2
    dy2=y3-y2
    return dx1,dy1,dx2,dy2

Ну, и собственно, код получения инвариантного описания:

coses=[]
coses.append(get_cos_edges(get_coords(polar_coordinates[size-1],polar_coordinates[0],polar_coordinates[1])))
for i in range(1,size-1):
    coses.append(get_cos_edges(get_coords(polar_coordinates[i-1], polar_coordinates[i],polar_coordinates[i+1])))
coses.append(get_cos_edges(get_coords(polar_coordinates[size-2], polar_coordinates[size-1],polar_coordinates[0])))

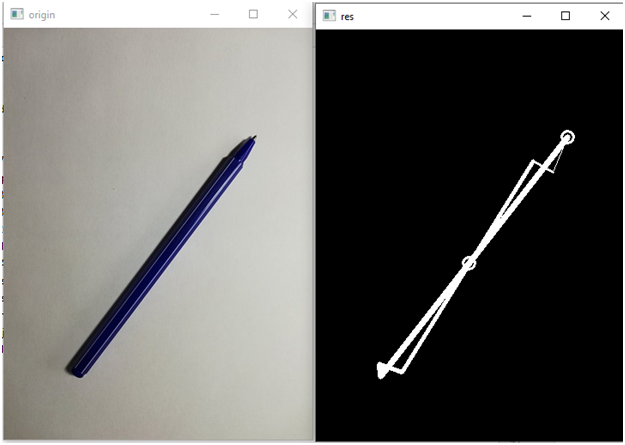
print(coses)

Запустим программу и посмотрим эти вектора для разных положений ручки:

Сформированный вектор:

[0.8435094506704439, -0.9679482843035412, -0.7475204740128089, 0.12575426475263257, -0.7530074822433576, -0.9513518107379842]

Посмотрим в другом положении:

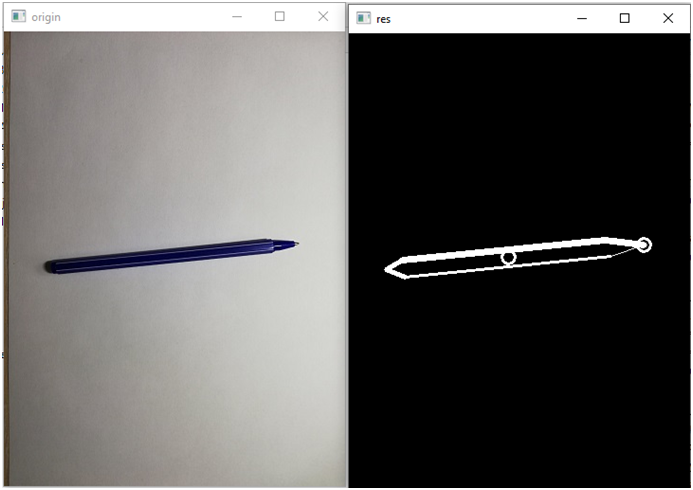
Сформированный вектор:

[0.8997284651496198, -0.9738348113021638, -0.886281044605172, 0.6119832801209469, -0.9073303511520623, -0.9760783176138438]

Как видим, первые две цифр оказались близкие, третья чуть дальше, четвертая сильно изменилась, так же предпоследняя, а вот последняя тоже почти совпала.

Для чистоты эксперимента, еще в одном положении:

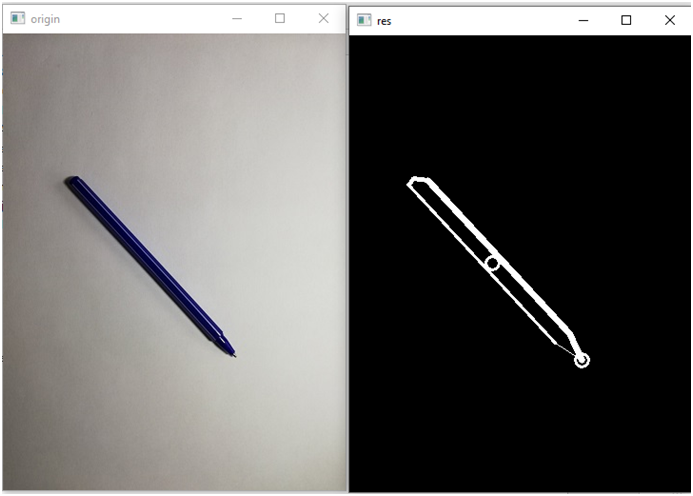
Вектор:

[0.8447017514267182, -0.968529494204698, -0.20124730714807806, -0.4685934718394871, -0.7702667523702886, -0.9517100095171195]

Видим аналогичную ситуацию.

Конечно, это не есть хорошо, что какие-то цифры вектора сильно «плывут» (опять тень мешает, будь она неладна). Это осложнит идентификацию. Но у нас еще есть другой вариант, который мы рассмотрим на следующем уроке. А сейчас, в заключение, урока, я приведу весь код примера:

import cv2
import numpy as np
import math
import os
img = cv2.imread("Samples/1.jpg")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
thresh = 100

def custom_sort(countour):
    return -countour.shape[0]

def polar_sort(item):
    return item[0][0]

def get_cos_edges(edges):
    dx1, dy1, dx2, dy2=edges
    r1 = math.sqrt(dx1 * dx1 + dy1 * dy1)
    r2 = math.sqrt(dx2 * dx2 + dy2 * dy2)
    return (dx1*dx2+dy1*dy2)/r1/r2

def get_polar_coordinates(x0,y0,x,y,xc,yc):
    #Первая координата в полярных координатах - радиус
    dx=xc-x
    dy=yc-y
    r=math.sqrt(dx*dx+dy*dy)

    #Вторая координата в полярных координатах - узел, вычислим относительно начальной точки
    dx0=xc-x0
    dy0=yc-y0
    r0 = math.sqrt(dx0 * dx0 + dy0 * dy0)
    scal_mul=dx0*dx+dy0*dy
    cos_angle=scal_mul/r/r0
    sgn=dx0*dy-dx*dy0 #опредедляем, в какую сторону повернут вектор
    if cos_angle>1:
        if cos_angle>1.0001:
            raise Exception("Что-то пошло не так")
        cos_angle=1
    angle=math.acos(cos_angle)
    if sgn<0:
        angle=2*math.pi-angle
    return angle,r

def get_coords(item1, item2, item3):
    _, point1 = item1
    _, point2 = item2
    _, point3 = item3
    x1, y1 = point1
    x2, y2 = point2
    x3, y3 = point3
    dx1=x1-x2
    dy1=y1-y2
    dx2=x3-x2
    dy2=y3-y2
    return dx1,dy1,dx2,dy2

#get threshold image
ret,thresh_img = cv2.threshold(gray, thresh, 255, cv2.THRESH_BINARY)

# find contours without approx
contours,_ = cv2.findContours(thresh_img,cv2.RETR_TREE,cv2.CHAIN_APPROX_NONE)
contours=list(contours)
contours.sort(key=custom_sort)
sel_countour=contours[1]

# calc arclentgh
arclen = cv2.arcLength(sel_countour, True)

# do approx
eps = 0.01
epsilon = arclen * eps
approx = cv2.approxPolyDP(sel_countour, epsilon, True)

sum_x=0.0
sum_y=0.0
for point in approx:
    x = float(point[0][0])
    y = float(point[0][1])
    sum_x+=x
    sum_y+=y
xc=sum_x/float(len((approx)))
yc=sum_y/float(len((approx)))

max=0
beg_point=-1
for i in range(0,len(approx)):
    point=approx[i]
    x = float(point[0][0])
    y = float(point[0][1])
    dx=x-xc
    dy=y-yc
    r=math.sqrt(dx*dx+dy*dy)
    if r>max:
        max=r
        beg_point=i

polar_coordinates=[]
x0=approx[beg_point][0][0]
y0=approx[beg_point][0][1]

for point in approx:
    x = int(point[0][0])
    y = int(point[0][1])
    angle,r=get_polar_coordinates(x0,y0,x,y,xc,yc)
    polar_coordinates.append(((angle,r),(x,y)))

polar_coordinates.sort(key=polar_sort)

img_contours = np.uint8(np.zeros((img.shape[0],img.shape[1])))
size=len(polar_coordinates)
for i in range(1,size):
    _ , point1=polar_coordinates[i-1]
    _, point2 = polar_coordinates[i]
    x1,y1=point1
    x2,y2=point2
    cv2.line(img_contours, (x1, y1), (x2, y2), 255, thickness=i)
_ , point1=polar_coordinates[size-1]
_, point2 = polar_coordinates[0]
x1,y1=point1
x2,y2=point2
cv2.line(img_contours, (x1, y1), (x2, y2), 255, thickness=size)

cv2.circle(img_contours, (int(xc), int(yc)), 7, (255,255,255), 2)

coses=[]
coses.append(get_cos_edges(get_coords(polar_coordinates[size-1],polar_coordinates[0],polar_coordinates[1])))
for i in range(1,size-1):
    coses.append(get_cos_edges(get_coords(polar_coordinates[i-1], polar_coordinates[i],polar_coordinates[i+1])))
coses.append(get_cos_edges(get_coords(polar_coordinates[size-2], polar_coordinates[size-1],polar_coordinates[0])))

print(coses)

point=approx[beg_point]
x = float(point[0][0])
y = float(point[0][1])
cv2.circle(img_contours, (int(x), int(y)), 7, (255,255,255), 2)

cv2.imshow('origin', img) # выводим итоговое изображение в окно
cv2.imshow('res', img_contours) # выводим итоговое изображение в окно

cv2.waitKey()
cv2.destroyAllWindows()