На прошлом уроке я рассказал о том, как повысить контрастность изображения и как выделить на изображении особе точки. Затем мы попробовали работать с найденными особыми точками. В частности, превратили эти точки в список  координат и попытались объединить близкие точки в одну, так как у нас получилось очень много точек рядом. В статье был предложен следующий алгоритм: при составлении списка, перед добавлением в список очередной точки проверять, находится ли она близко от последней, если да, то добавлять в тот же список, если нет, то начинать новый список.  Только проблема в том, что обход точек был через развертку, и могло получиться так, что близкие точки попадают в разные списки. Поэтому объединение точек получилось «криво».  Сегодня мы исправим этот недочет.

Для начала, почему мы вообще начали все эти хитрости с алгоритмом? Дело в том, что если решать задачу «в лоб», то время работы алгоритма у нас будет пропорционально квадрату размера списка. Собственно, давайте сначала проверим, насколько критично будет время работы алгоритма «в лоб» при разных ситуациях. И так, нам нужно перебрать все точки и сравнить их расстояния со всеми точками:

#Сначала создадим список точек
heigh=img_blank.shape[0]
width=img_blank.shape[1]
points=[]
for x in range(0,width):
    for y in range(0,heigh):
        if img_blank[y,x,2]==255:
            points.append((x,y))

#Теперь будем обрабатывать этот список
points_count=len(points)
print("Количество обрабатываемых точек: ",points_count)
beg_time=time.perf_counter()
lists=[0]*points_count
for i in range(0,points_count):
    for j in range(i+1,points_count):
        p1=points[i]
        p2=points[j]
        if p1==0 or p2==0:
            continue
        r=get_distance(p1,p2)
        if r<10:
            if lists[i]==0:
                lists[i]=[]
            lists[i].append(p2)
            points[j]=0
end_time=time.perf_counter()
print("Прошло времени ",end_time-beg_time)

centers=[]
for ls in lists:
    if ls!=0:
        centers.append(calk_center(ls))

print("Осталось точек ",len(centers))

Вот что у нас вышло:

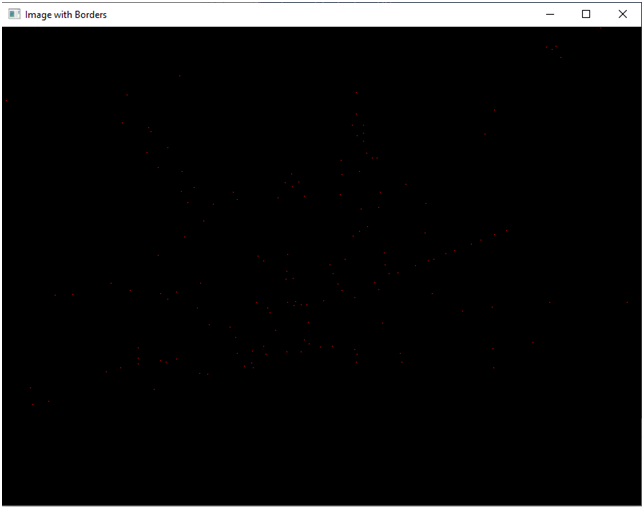
На моем компе (Intel(R) Core(TM) i3-8350K CPU @ 4.00GHz   4.01 GHz, памяти 16 Гб) время работы составило 0,5 секунды. Точек, напоминаю, 2829, после обработки осталось 146.  Для разового запуска это, конечно, мелочь, а вот для программы, работающей в режиме реального времени, это критично. Хуже, если кол-во точек повысить. В своем эксперименте я повысил их количество до 12247, просто поменяв порог чувствительности. Теперь программа выполнялась уже 10 секунд, оставив после объединения 455 точек.

Как же решить эту проблему? Если честно, то обсуждение теории алгоритмов выходит за рамки цикла уроков о компьютерном зрении, но все-таки, я поделюсь с вами одной идейкой, как ускорить процесс объединения точек. Не нужно перебирать список для каждого из его элементов. Можно перебрать его один раз, сразу помещая элемент (точку) в определенный список (кластер). Правда, тут, возникает проблема. Мы не знаем заранее, какие будут кластеры. Не беда. Давайте создавать их по мере перебора. Сначала у нас нет ни одного кластера. Поэтому мы создаем один и помещаем в него нашу точку. Точнее, помещать ее не нужно. Просто запомним ее координаты, а для следующих точек будем корректировать эти координаты кластера, которые, по сути, центр масс входящий в кластер точек. Если окажется, что точка слишком далека от центра кластера, создаем точно так же новый кластер. Вот, собственно, и сам алгоритм:

# Python программа для иллюстрации
# обнаружение угла с
# Метод определения угла Харриса

import cv2
import numpy as np
import math
import time

#Вычслить расстояние между точками
def get_distance(p1,p2):
    x1,y1=p1
    x2,y2=p2
    l = math.sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2))  # Евклидово расстояние между последней и текущей точкой
    return l

#получить центр масс точек
def get_center(centers, point):
    l=len(centers)
    res=-1
    min_r=9999999999999.0
    for i in range(0,l):
        center=centers[i]
        x,y,count=center
        r=get_distance(point,(x,y))
        if r>=10:
            continue
        if r<min_r:
            res=i
            min_r=r
    return res

#Добавить точку в центр масс
def add_to_center(center, point):
    x1,y1,count=center
    count+=1
    x2,y2=point
    x=x1+(x2-x1)/float(count)
    y=y1+(y2-y1)/float(count)
    return x,y,count

# путь к указанному входному изображению и
# изображение загружается с помощью команды imread
image = cv2.imread('DSCN1311.jpg')

# конвертировать входное изображение в Цветовое пространство в оттенкахсерого
operatedImage = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# изменить тип данных
# установка 32-битной плавающей запятой
operatedImage = np.float32(operatedImage)

# применить метод cv2.cornerHarris
# для определения углов с соответствующими
# значения в качестве входных параметров
dest = cv2.cornerHarris(operatedImage, 2, 5, 0.07)

# Результаты отмечены через расширенные углы
dest = cv2.dilate(dest, None)

# Возвращаясь к исходному изображению,
# с оптимальным пороговым значением
img_blank = np.zeros(image.shape)
img_blank[dest > 0.05 * dest.max()] = [0, 0, 255]

#Сначала создадим список точек
heigh=img_blank.shape[0]
width=img_blank.shape[1]
points=[]
for x in range(0,width):
    for y in range(0,heigh):
        if img_blank[y,x,2]==255:
            points.append((x,y))

#Теперь будем обрабатывать этот список
points_count=len(points)
print("Количество обрабатываемых точек: ",points_count)
beg_time=time.perf_counter()
centers=[]

for i in range(0,points_count):
    point=points[i]
    center_index=get_center(centers,point)
    if center_index==-1:
        x,y=point
        centers.append((x,y,1))
    else:
        center = centers[center_index]
        centers[center_index]=add_to_center(center,point)
end_time=time.perf_counter()
print("Прошло времени ",end_time-beg_time)

print("Осталось точек ",len(centers))

img_blank1 = np.zeros(image.shape)
for center in centers:
    x,y,count=center
    img_blank1[int(y),int(x),2]=255

# окно с выводимым изображением с углами
cv2.imshow('Image with Borders', img_blank1)

if cv2.waitKey(0) & 0xff == 27:
    cv2.destroyAllWindows()

Теперь программа выполнялась 0.08 сек, и осталось после объединения 127 точек. «Что-то не сходиться», - скажете вы. Да, совершенно верно, результаты будут отличаться от тех, что были в предыдущем алгоритме. Да, мы ускорили обработку, но немного пожертвовали точностью.

Теперь поговорим о том, как нам этот набор точек превратить в граф. Чисто для того, чтобы научится, построим самый примитивный граф: начнем построение с какой-нибудь точки, соединим ее с ближайшей, ту со следующей ближайшей и так до тех пор, пока не обойдем все точки.  Это называется жадный алгоритм, и мы, по сути, решили задачу коммивояжера,  которая состоит в том, чтобы обойти все пункты по кратчайшему пути (ну, или почти по кратчайшему).  Поясню почему «почти по кратчайшему». Дело в том, что задача коммивояжера относится к классу NP-трудных задач. Наикратчайший путь возможно найти только полным перебором, но беда в том, что с увеличением количества пунктов время полного перебора возрастает очень резко. Алгоритмическая сложность такой задачи O(n!). То есть, если количество пунктов, которые надо обойти, равно 20, то нам потребуется 2 432 902 008 176 640 000 итераций. Пусть даже в секунду компьютер делает миллиард итераций, тогда для отработки алгоритма потребуется примерно 77 лет. А если итераций будет 21, то времени потребуется еще в 21 больше.  В общем, ясно, что полный перебор в данном случае – это не метод решения. Поэтому задачу поиска наикратчайшего пути заменяют задачей нахождение более-менее короткого пути («почти наикратчайшего» как было замечено выше).

В качестве «какой-нибудь» точки мы возьмем центр наиболее «весомого» кластера (того, за который «проголосовало» наибольшее количество рядом стоящих точек). Вот как мы его найдем, одновременно рисуя точки на экране:

img_blank1 = np.zeros(image.shape)
max=0
beg_point=None
for center in centers:
    x,y,count=center
    cv2.circle(img_blank1, (int(x),int(y)), 3,  (0, 0, 255), 2)
    if count>max:
        max=count
        beg_point=center

Потом, конечно, удалим эту точку из списка, и создадим список ребер графа:

centers.remove(beg_point)
graph=[]

Осуществим обход точек жадным алгоритмом, так как точек немного, можно решить задачу «в лоб»,  то есть через полный перебор точек в двойном цикле:

while len(centers)>0:
    min=999999999999
    next_point=None
    for center in centers:
        x1,y1,_=beg_point
        x2,y2,_=center
        r=get_distance((x1,y1),(x2,y2))
        if r<min:
            min=r
            next_point=center
    graph.append((beg_point,next_point))
    centers.remove(next_point)
    beg_point=next_point

Ну, и наконец, переберем наши ребра, чтобы отобразить их на экране:

for edge in graph:
    p1,p2=edge
    x1,y1,_=p1
    x2,y2,_=p2
    cv2.line(img_blank1, (int(x1), int(y1)), (int(x2), int(y2)), (255, 0, 0), thickness=1)

Вот что у нас получится:

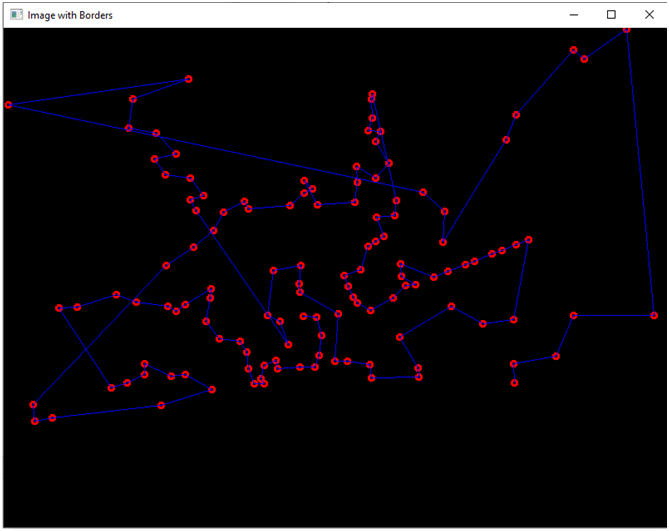
Возможно, кто-то спросит: «А какова практическая польза в этих вот красивых построения?». Отвечу. Вот представьте, что вам надо распознать на изображении какой-то объект (например, котика, человеческое лицо, дом, автомобиль). Сложность задачи заключается в том, что объект может находится в разных местах картинки, он может быть повернут под различным углом, может быть большим или маленьким (далеким и близким). Кроме того, объект может быть снят с разных ракурсов. Таким образом, нам необходимо каким-то образом сделать так, чтобы объект был инвариантен к переносу, к вращению, к изменению размера, и, желательно, к аффинным преобразованиям. Граф – это как раз пример такой структуры. Вот смотрите. Если у нас имеются координаты каких-то особых точек объекта, то при изменении его положения координаты точек изменятся. А если мы соединим некоторые точки линиями, и измерим расстояния между ними? Длины отрезков к изменению положения уже инварианты, сколько ни смещай объект, длины не изменятся. Более того, они инвариантны даже к вращению! А если мы возьмем не длины отрезков, а углы между ними? Тогда описание объекта станет инвариантным к изменению размеров (помните из школы теорему, что углы подобных треугольников равны?). А с графов мы вообще можем по всякий «извращаться».

В общем, мы сделали первый шаг к тому, чтобы выделять на изображениях фичи и работать с ними. На этой оптимистичной ноте я закончу этот урок, до новых встреч. В заключении полный текст программы данного примера (который строит граф):

# Python программа для иллюстрации
# обнаружение угла с
# Метод определения угла Харриса

import cv2
import numpy as np
import math
import time
import functools

#функция сравнения для сортировки спсика
def compare_function(item1, item2):
    _, _, count1 = item1
    _, _, count2 = item2
    if count1 < count2:
        return 1
    if count1 > count2:
        return -1
    return 0

#Вычслить расстояние между точками
def get_distance(p1,p2):
    x1,y1=p1
    x2,y2=p2
    l = math.sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2))  # Евклидово расстояние между последней и текущей точкой
    return l

#получить центр масс точек
def get_center(centers, point):
    l=len(centers)
    res=-1
    min_r=9999999999999.0
    for i in range(0,l):
        center=centers[i]
        x,y,count=center
        r=get_distance(point,(x,y))
        if r>=10:
            continue
        if r<min_r:
            res=i
            min_r=r
    return res

#Добавить точку в центр масс
def add_to_center(center, point):
    x1,y1,count=center
    count+=1
    x2,y2=point
    x=x1+(x2-x1)/float(count)
    y=y1+(y2-y1)/float(count)
    return x,y,count

# путь к указанному входному изображению и
# изображение загружается с помощью команды imread
image = cv2.imread('DSCN1311.jpg')

# конвертировать входное изображение в Цветовое пространство в оттенкахсерого
operatedImage = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# изменить тип данных
# установка 32-битной плавающей запятой
operatedImage = np.float32(operatedImage)

# применить метод cv2.cornerHarris
# для определения углов с соответствующими
# значения в качестве входных параметров
dest = cv2.cornerHarris(operatedImage, 2, 5, 0.07)

# Результаты отмечены через расширенные углы
dest = cv2.dilate(dest, None)

# Возвращаясь к исходному изображению,
# с оптимальным пороговым значением
img_blank = np.zeros(image.shape)
img_blank[dest > 0.05 * dest.max()] = [0, 0, 255]

#Сначала создадим список точек
heigh=img_blank.shape[0]
width=img_blank.shape[1]
points=[]
for x in range(0,width):
    for y in range(0,heigh):
        if img_blank[y,x,2]==255:
            points.append((x,y))

#Теперь будем обрабатывать этот список
points_count=len(points)
print("Количество обрабатываемых точек: ",points_count)
beg_time=time.perf_counter()
centers=[]

for i in range(0,points_count):
    point=points[i]
    center_index=get_center(centers,point)
    if center_index==-1:
        x,y=point
        centers.append((x,y,1))
    else:
        center = centers[center_index]
        centers[center_index]=add_to_center(center,point)
end_time=time.perf_counter()
print("Прошло времени ",end_time-beg_time)

print("Осталось точек ",len(centers))

img_blank1 = np.zeros(image.shape)
max=0
beg_point=None
for center in centers:
    x,y,count=center
    cv2.circle(img_blank1, (int(x),int(y)), 3,  (0, 0, 255), 2)
    if count>max:
        max=count
        beg_point=center

centers.remove(beg_point)
graph=[]

while len(centers)>0:
    min=999999999999
    next_point=None
    for center in centers:
        x1,y1,_=beg_point
        x2,y2,_=center
        r=get_distance((x1,y1),(x2,y2))
        if r<min:
            min=r
            next_point=center
    graph.append((beg_point,next_point))
    centers.remove(next_point)
    beg_point=next_point

for edge in graph:
    p1,p2=edge
    x1,y1,_=p1
    x2,y2,_=p2
    cv2.line(img_blank1, (int(x1), int(y1)), (int(x2), int(y2)), (255, 0, 0), thickness=1)



# окно с выводимым изображение графа
cv2.imshow('Image with Borders', img_blank1)

if cv2.waitKey(0) & 0xff == 27:
    cv2.destroyAllWindows()