Когда я взялась решать задачку по динамическому программированию — реализовать алгоритм, который рассчитывает расстояние Левенштейна — мне пришлось послушать пару небольших лекций и прочесть несколько статей (приведу их в конце), чтобы разобраться. Я решила попытаться пересказать алгоритм настолько просто, чтобы по этому объяснению можно было снять ролик для тиктока (когда он снова возобновит свою деятельность в РФ). Дальше — мало формул и много картинок.

Понятие редакционного расстояния

Расстояние Левенштейна, или редакционное расстояние, — метрика cходства между двумя строковыми последовательностями. Чем больше расстояние, тем более различны строки. Для двух одинаковых последовательностей расстояние равно нулю. По сути, это минимальное число односимвольных преобразований (удаления, вставки или замены), необходимых, чтобы превратить одну последовательность в другую.

Например, LEV(’БИБА’, ‘БОБА’) = 1, так как потребуется провести одну замену ‘И’ на ‘О’:

Расстояние между Австрией и Австралией по Левенштейну составит 2 — понадобится два удаления:

А вот между котиком и скотиной — 3 — две вставки и одна замена:

Существует также модификация метрики — расстояние Дамерау — Левенштейна, в котором добавлена операции перестановки символов. В данной статье мы не будем его рассматривать.

Практическое применение

Расстояние Левенштейна активно используется для исправления ошибок в словах, поиска дубликатов текстов, сравнения геномов и прочих полезных операций с символьными последовательностями.

Метрика названа в честь советского математика, выпускника мехмата МГУ Владимира Иосифовича Левенштейна. Он всю жизнь проработал в Институте Прикладной Математики им. М.В.Келдыша, умер в 2017 году.

Алгоритм Вагнера — Фишера

Итак, вычислим расстояние между двумя строками методом Вагнера — Фишера: составим матрицу D и каждый её элемент вычислим по рекуррентной формуле:

Немного пугает? Разберёмся, как использовать формулу для заполнения таблицы.

Ясно, что первые три строчки рекуррентной формулы помогут нам заполнить только первый столбец и первую строку таблицы. Для всех остальных ячеек мы будем пользоваться четвёртой строкой — той, что с минимумом. Здесь— символы, соответствующие ячейкам i и j. Оператор если символы и не равны друг другу, и если равны.

Обратите внимание, что первый символ последовательности будет иметь индекс 1, как принято в математике, а не 0.

Будем заполнять таблицу построчно.

Рассчитаем D(1,1), это символы ‘Г’ и ‘Л’. Они не равны друг другу, значит m(’Г’, ‘Л’) = 1. Тогда D(1,1) — это минимум между значениями D(0,1) + 1, D(1,0) + 1 и D(0, 0) + m(’Г’, ‘Л’) = D(0, 0) + 1. Эти клетки выделены голубым. То есть min(1+1, 1+1, 0+1) = min(2, 2, 1) = 1.

Рассчитаем следующую клетку, D(1, 2). Для этого просто сдвинем голубой уголок на одну клетку вправо:

Так как символы ‘Г’ и ‘А’ не равны, используем ту же формулу:

D(1, 2) = min(D(0,2) + 1; D(1,1) + 1; D(0, 1) + 1) = min(2+1; 1+1; 1+1) = 2.

Передвигая голубой уголок, аналогично заполним первые две строки и начало третьей, пока не доберёмся до совпадающих символов ‘Б’ в D(3,3):

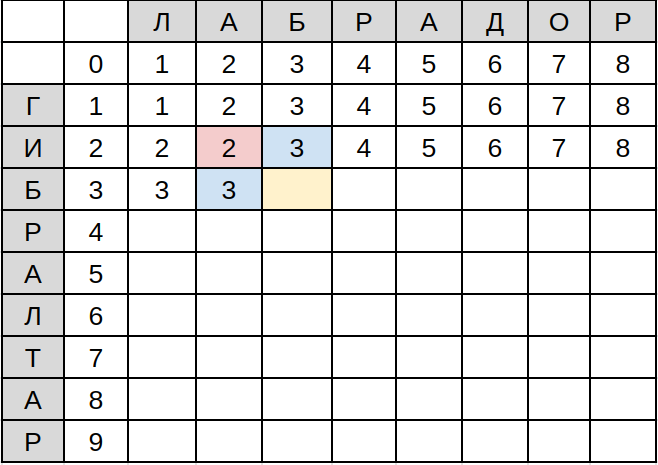
Из-за того, что символы совпадают, замена этим двум символам не нужна, поэтому при подсчёте минимума число в розовой ячейке не увеличивается на единицу, т.е. D(3, 3) = min(D(2,3) + 1; D(3,2) + 1; D(2, 2) + 0) = min(3+1; 3+1; 2+0) = 2.

Заполняем таким образом таблицу до самого конца.

Расстояние Левенштейна в этой мартице — нижняя правая ячейка, D(9,8):

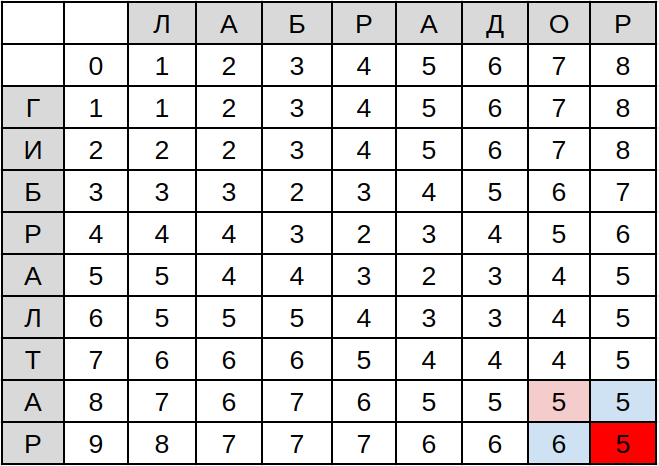
Ура! Нам понадобится 5 шагов, чтобы превратить Гибралтар в лабрадора.

Если вас интересует только понимание алгоритма, а не его реализация в коде, на этом всё.

Реализация в динамическом программировании

Если же реализовать всё-таки нужно, посмотрим, как это сделать на Python.

Так как мы заполняем матрицу, нам понадобится 2 цикла, длины которых равны длинам символьных последовательностей, которые мы хотим сравнить или преобразовать.

В целях минимизации используемой памяти мы располагаем строковые последовательности так, чтобы длины строк были минимальны. Это необязательно, но существенно сэкономит память, если одна из последовательностей длинная, а другая короткая.

def levenshtein(str_1, str_2):
    n, m = len(str_1), len(str_2)
    if n > m:
        str_1, str_2 = str_2, str_1
        n, m = m, n

Ясно, что хранить всю матрицу в памяти не нужно* — достаточно текущей и предыдущей строк. Циклы начинаются с 1 — так же, как индексы в таблице:

*нужно в случае, если задача стоит не посчитать расстояние, а составить редакционное предписание: последовательность односимвольных операций (вставок, удалений и замен), в результате которой одна последовательность превратится в другую. Эта задача сложнее формализуется, поэтому выходит за рамки данной статьи.

  current_row = range(n + 1)
  for i in range(1, m + 1):
		  previous_row, current_row = current_row, [i] + [0] * n

Проще основным случаем считать тот, когда символы равны, и в случае, если нет — прибавлять к ячейке в предыдущей строке по диагонали (розовой) единицу:

for j in range(1, n + 1):
		add, delete, change = previous_row[j] + 1, current_row[j - 1] + 1, previous_row[j - 1]
		if str_1[j - 1] != str_2[i - 1]:
			   change += 1
		current_row[j] = min(add, delete, change)

Весь алгоритм в таком случае будет выглядеть так:

def levenstein(str_1, str_2):
    n, m = len(str_1), len(str_2)
    if n > m:
        str_1, str_2 = str_2, str_1
        n, m = m, n

    current_row = range(n + 1)
    for i in range(1, m + 1):
        previous_row, current_row = current_row, [i] + [0] * n
        for j in range(1, n + 1):
            add, delete, change = previous_row[j] + 1, current_row[j - 1] + 1, previous_row[j - 1]
            if str_1[j - 1] != str_2[i - 1]:
                change += 1
            current_row[j] = min(add, delete, change)

    return current_row[n]

В данной реализации цены замены, удаления и вставки равны друг другу и единице, но, в зависимости от задачи, они могут принимать неравные значения.

Время работы этого алгоритма — m*n, т.е. равно произведению длин символьных последовательностей.

Когда не нужно изобретать велосипед

В коммерческой разработке и/или при обработке больших массивов слов писать метод самостоятельно чаще всего нет смысла. В Python есть библиотека, в оригинале написанная на C, а также библиотека, содержащая разные метрики оценки сходства строк. Также можно посчитать расcтояние в NLTK.

Заключение

На мой взгляд, разбор алгоритма вычисления расстояния Левенштейна — не только хорошая задачка для собеседования, но и просто увлекательное занятие. Заполнение таблицы напомнило мне азиатскую игру Го.

Здорово, когда не просто пользуешься реализацией алгоритма из коробки, но и понимаешь, как именно всё работает. Надеюсь, после этой статьи у вас стало на один такой алгоритм больше.

Литература

• https://medium.com/analytics-vidhya/levenshtein-distance-for-dummies-dd9eb83d3e09

• https://habr.com/ru/post/117063/

• https://tirinox.ru/levenstein-python/