Когда моя сестра переехала в другой город и познакомилась с соседями, оказалось, что дедушка и бабушка ее соседа и наши бабушка с дедушкой были хорошими друзьями и общались, живя рядом в другом городе – два поколения назад. Интересно, когда обнаруживаются такие неожиданные связи. Согласно теории сетей, пути, соединяющие узлы сети, зачастую короче, чем могло бы показаться.

Если каждый в сети знает k других людей, то можно упрощенно предположить, что, начав от этого человека и совершив n переходов от узла к узлу, мы найдем kⁿ человек. Учитывая экспоненциальный рост, потребуется совсем немного времени, чтобы построить путь от любого конкретного человека до любого другого в графе.

Но в реальных социальных сетях многие люди, знакомые конкретному человеку, также знают друг друга. Такое пересечение между друзьями друзей снижает количество новых людей, к которым я могу обратиться после каждого перехода на пути от стартового узла.  Может быть непросто найти такие пути, которые начинаются в сплоченном сообществе, а далее разветвляются до самых отдаленных уголков сети.

В главе 20 книги Networks Crowds and Markets ее авторы Дэвид Изли и Джон Клейнберг дают теоретический аппарат, описывающий, как в реальном мире могут возникать феномены, укладывающиеся в граф «мир тесен». В этой теории сочетается идея гомофилии, согласно которой схожие люди кучкуются вместе, и идея слабых связей, где отношения ветвятся в масштабах всей сети. Объяснение основано на работе Дункана Уоттса и Стива Строгаца. Давайте проследим эти примеры при помощи кода, написанного при помощи Neo4j.

Чтобы выполнить приведенный ниже код, войдите в песочницу и выберите “New Project.” (Новый проект). Далее из предлагаемых заготовок проектов выберите  “Graph Data Science”.

В песочницу загружен большой объем данных по «Игре престолов», которые не понадобятся нам для этого упражнения. Давайте их удалим.

MATCH (n) 
DETACH DELETE n;

Теперь заложим сетку из узлов Person, 30 на 30. Каждый узел Person получит три свойства: строку, столбец и координаты.

UNWIND RANGE(1,30) AS row
UNWIND RANGE(1,30) AS column
CREATE (p:Person {row:row, column:column, 
     coordinates:toString(column) + ', ' + toString(row)});

Создаем отношения KNOWS между каждым конкретным лицом и лицом, расположенным в сетке справа от него.

MATCH (p1:Person), (p2:Person)
WHERE p1.row = p2.row
     AND p1.column = p2.column - 1
CREATE (p1)-[:KNOWS]->(p2);

Создаем отношения KNOWS между каждым конкретным лицом и лицом, расположенным в сетке строго под ним.

MATCH (p1:Person), (p2:Person)
WHERE p1.column = p2.column
     AND p1.row = p2.row - 1
CREATE (p1)-[:KNOWS]->(p2);

Между каждым конкретным лицом и двумя лицами, смежными с ним по диагонали и находящимися на ряд ниже.

MATCH (p1:Person)-->(p2:Person)
WHERE p1.row = p2.row-1
WITH (p1), (p2)
MATCH (p2)--(p3)
WHERE p3.row = p2.row
CREATE (p1)-[:KNOWS]->(p3);

У нас получился красивый решетчатый паттерн. Выбираем Person и их соседей, а далее посмотрим, как работают эти взаимоотношения.

MATCH (p:Person {row:5, column:5})--(n) 
RETURN *;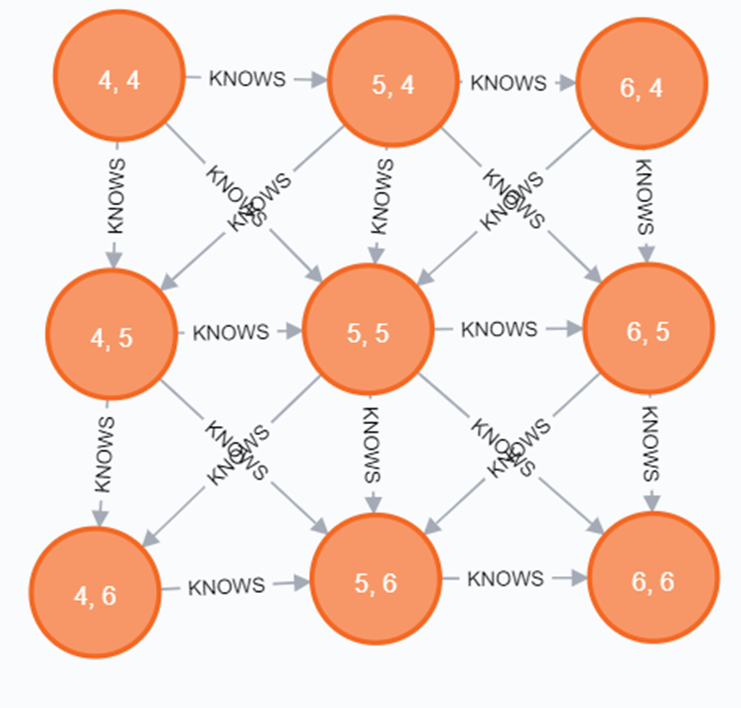

Я вижу на этой картинке множество треугольников. Воспользуемся библиотекой для data science на графах, чтобы определить, какова пропорция таких людей в кругу знакомых данного человека, которые также знают друг друга. Сначала создадим в памяти именованный граф.

CALL gds.graph.create('base-grid', 'Person', {KNOWS:
     {orientation:"UNDIRECTED"}});

Далее выполним алгоритм подсчета треугольников.

CALL gds.alpha.triangleCount.stream('base-grid') 
YIELD  coefficient
RETURN avg(coefficient) AS averageClusteringCoefficient

Результат 0,44 означает, что в среднем лишь около половины знакомых конкретного человека также знакомы друг с другом. Такой уровень перекрытия соседей может обусловить сравнительно длинные пути по сравнению с теми, которые мы могли бы ожидать в сети, где большинство узлов имеет степень 8.

Проверим эту идею. Вызовем процедуру allShortestPaths, чтобы найти кратчайший путь между каждыми двумя узлами в графе. Далее обобщим результаты.

CALL gds.alpha.allShortestPaths.stream('small-world')
YIELD sourceNodeId, targetNodeId, distance
RETURN max(distance) AS maxDistance, 
     min(distance) AS minDistance, 
     avg(distance) AS avgDistance, 
     count(distance) AS pathCount;

Я был впечатлен, что мой бесплатный сервер-песочница смог вычислить 809 100 путей примерно за секунду. Диаметр графа – это самый длинный из кратчайших путей между узлами. Диаметр в 29 переходов в этом графе вполне логичен. Никакие два узла не будут находиться дальше друг от друга, чем расположенные на противоположных краях сетки.

Рассмотрим распределение длин путей.

CALL gds.alpha.allShortestPaths.stream('base-grid')
YIELD sourceNodeId, targetNodeId, distance
RETURN distance, count(*) AS pathCount
ORDER BY distance;

Вот схема с результатами.

Теперь давайте изменим граф, добавив в него случайные взаимосвязи между такими узлами, которые не являются смежными в сетке. Можно сравнить эти слабые связи с такими отношениями: есть некоторые люди, которых вы знаете, но которые выпадают из основного круга ваших друзей.

Воспользуемся процедурой apoc.periodic.iterate, чтобы перебрать все узлы и добавить к каждому узлу две несмежных связи.

CALL apoc.periodic.iterate(
     'MATCH (p1) RETURN p1',
     'MATCH (p2)
      WHERE p1 <> p2 AND NOT EXISTS((p1)--(p2))
      WITH p1, p2, rand() AS rand
          ORDER BY rand LIMIT 2
      MERGE (p1)-[:KNOWS {adjacent:False}]->(p2)',
     {batchSize:1}
)

Давайте вновь взглянем на Person с координатами  5, 5. Теперь у этого узла десять связей. Восемь из них в сетке являются смежными, а две новых связи – несмежные.

MATCH (p:Person {row:5, column:5})--(n) 
RETURN *;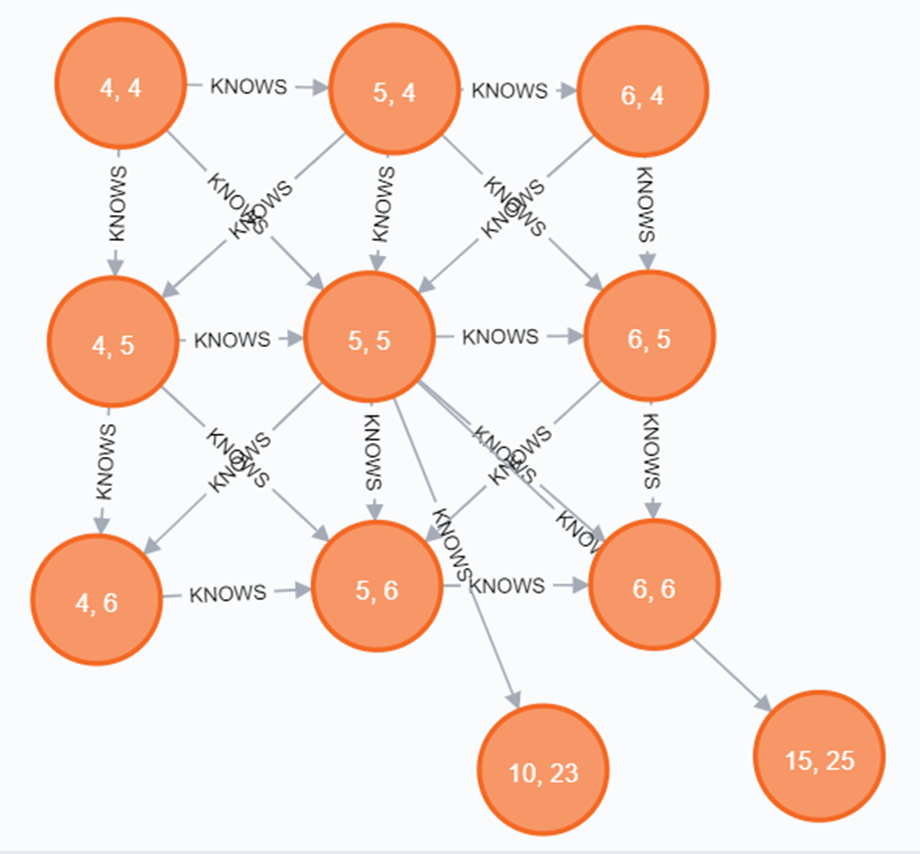

Создадим в памяти новый граф, который проанализируем при помощи библиотеки Graph Data Science Library.

CALL gds.graph.create('small-world', 'Person', 
     {KNOWS:{orientation:"UNDIRECTED"}});

Каков средний коэффициент кластеризации для нового графа?

CALL gds.alpha.triangleCount.stream('base-grid') 
YIELD  coefficient
RETURN avg(coefficient) AS averageClusteringCoefficient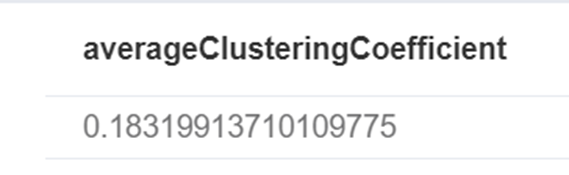

В новом графе в среднем насчитывается 18% человек, которые знают рассматриваемого человека и при этом знают друг друга. При появлении двух новых друзей на каждого человека и меньшим пересечением между друзьями должны находиться более короткие пути между узлами.

Давайте повторно прогоним allShortestPaths и проверим статистику.

CALL gds.alpha.allShortestPaths.stream('small-world')
YIELD sourceNodeId, targetNodeId, distance
RETURN max(distance) AS maxDistance, 
     min(distance) AS minDistance, 
     avg(distance) AS avgDistance, 
     count(distance) AS pathCount;

Диаметр графа резко уменьшился с 29 до 5, а средняя дистанция сократилась всего до 3. И вправду мир тесен!

Рассмотрим новое распределение длин путей.

CALL gds.alpha.allShortestPaths.stream('small-world')
YIELD sourceNodeId, targetNodeId, distance
RETURN distance, count(*) AS pathCount
ORDER BY distance;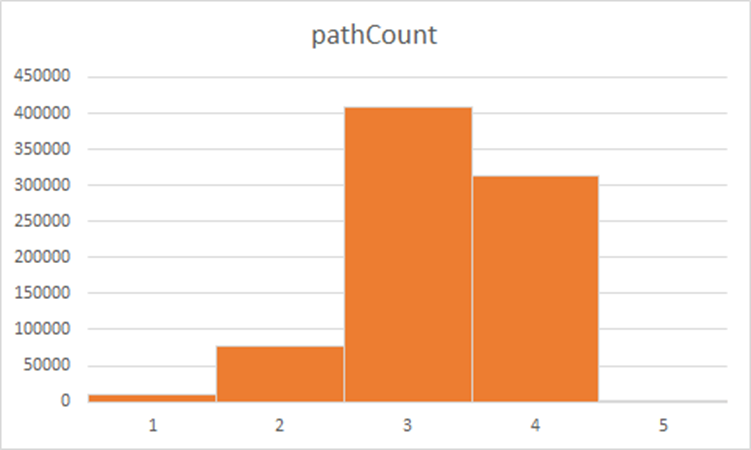

Очень мал процент таких людей, которые отстоят друг от друга на пять переходов. Огромное большинство кратчайших путей теперь включают по три-четыре перехода.

Мы начали с сети, где каждый знал только своих прямых соседей. Добавив по две несмежных связи для каждого узла, мы резко снизили диаметр графа и среднюю длину кратчайшего пути. Можно заново прогонять код с большим или меньшим количеством несмежных связей для каждого узла и посмотреть, как меняются результаты. Изли и Клейнберг показывают, что модель «мир тесен» развивается даже в случае, когда не у каждого человека есть несмежные связи. При создании единственной несмежной связи для подмножества узлов все равно удается существенно сократить длину путей между узлами.