Привет, меня зовут Герман, я занимаюсь С++ разработкой анимаций и графического движка в Константе.

Введение

Если ты сейчас здесь, скорее всего, тебе интересна компьютерная графика и фотореалистичный рендеринг. В этой статье я постарался рассказать об основных понятиях и объяснить базовые принципы трассировки лучей. Если внимательно ее прочитать, в конце можно получить правдоподобную фотографию мыльного пузыря и не только.

Что такое трассировка лучей

Я предполагаю, что мои читатели уже знакомы с понятиями вектора, матрицы, системы координат и имеют базовое представление о графическом пайплайне и шейдерах GLSL. Мы будем заниматься трассировкой лучей, поэтому для начала хорошо бы понять, что это за зверь. Итак, трассировка лучей - это набор алгоритмов и инструментов в компьютерной графике, позволяющий получать реалистичные рендеры. Название метода говорит само за себя: мы берем источник света и следим за тем, как испускаемые им лучи взаимодействуют с окружающей средой (отражаются и преломляются) перед тем, как быть воспринятыми человеческим глазом.

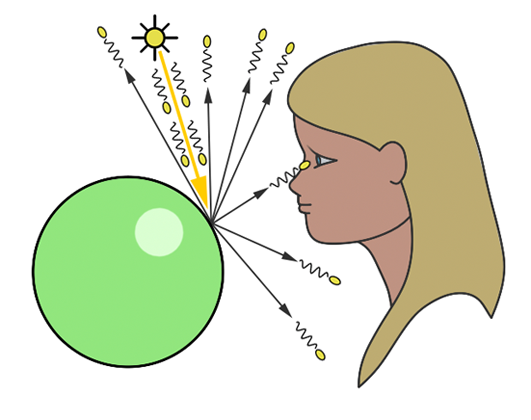
При этом далеко не все лучи достигают наблюдателя. При программировании такого алгоритма трассировки лучей, который еще называется "прямой", нам придется выпускать очень много лучей для получения изображения на экране. Посмотрим на рисунок 4: в первые секунды рендера большая часть лучей не достигла наблюдателя, из-за чего наблюдается картина с черными пятнами на изображении. Спустя же некоторое время, основная часть лучей, составляющих кадр сцены, достигает наблюдателя (рис. 5), и мы получаем итоговый рендер. Проблема в том, что прямой алгоритм, хотя и лучше описывает процесс распространения света, достаточно трудоемкий, и его не получится использовать для графики в реальном времени на большинстве современных систем. Но у нас есть решение этой проблемы: а что, если мы будем выпускать лучи не из источника света, а от наблюдателя, т.е. рассматривать только те лучи, которые нас достигли. Тогда нам не придется тратить лишнее время на "ожидание" прихода луча к наблюдателю. Такой алгоритм называется маршевым методом или обратной трассировкой лучей.

Маршевый метод или обратная трассировка лучей

Прежде чем говорить о самом алгоритме, нам нужно рассмотреть очень важный объект: знаковую функцию расстояния (Signed Distance Function, далее SDF). Она возвращает кратчайшее расстояние между заданной точкой в пространстве и некоторой поверхностью. Знак возвращаемого значения указывает, находится ли точка внутри этой поверхности или снаружи (отсюда название "функция расстояния со знаком"). Давайте покажу на примере.

Пример

В качестве примера рассмотрим SDF для сферы с радиусоми центром в точке . Тогда расстояние от точки до сферы будет определяться следующим образом:

Главной особенностью SDF является то, что по знаку значения функции в точке в пространстве сцены можно понять расположение этой точки относительно объекта (сфера, куб, плоскость и тп), расстояния до которого возвращает SDF. Возьмем случайную точку , если значение , то точка лежит вне объекта, если же , то точка находится внутри объекта и, наконец, если , точка лежит в точности на поверхности объекта. Заметим, что в реальных вычислениях можно считать, что точка лежит на поверхности объекта если значение , т.е. достаточно мало.

Так как дальше мы будем оперировать векторами, нам будут нужны векторные варианты записи формул для нахождения расстояний. В качестве примера векторный вид формулы SDF для сферы будет выглядеть так:

На языке glsl это запишется так:

float sphereSDF(vec3 p) {
    return length(p) - 1.0;
}

Функции расстояния для других объектов вы можете посмотреть здесь.

Теперь мы можем приступить к самому алгоритму обратной трассировки лучей. Прежде всего у нас есть плоскость экрана, которая состоит из пикселей. Давайте определим положение взгляда (камеры), тогда изображение, которое мы хотим получить, будет проецироваться на сетку (рис. 6), причем каждый узел сетки совпадает с пикселем выходного изображения. Таким образом, мы выпускаем лучи через каждый пиксель изображения и, если луч во что-то врезался (т.е. оказался на поверхности объекта, т.е. значение ), красим этот пиксель в цвет объекта.

Прежде всего мы должны определить направление лучей для трассировки. Для этого воспользуемся значением координаты пикселя изображения (gl_FragCoord). Векторы, образованные позицией взгляда и координатой конкретного пикселя (уже в нормализованных координатах), мы будет умножать на матрицы view и projection о которых можно более подробно прочитать здесь.

В обратной трассировке вся сцена определяется в терминах функции расстояния со знаком. Чтобы найти пересечение между лучом обзора и объектами на сцене, мы начинаем из стартовой позиции, совпадающей с положением взгляда в направлении вычисленного выше луча. На каждом шаге мы вычисляем значение SDF для каждого из объектов на сцене, получая значения Для того, чтобы понять, какой объект ближе всего к лучу, мы находим минимальное Далее, в зависимости от найденного значения, мы понимаем положение луча на сцене. Если значение достаточно мало, значит мы во что-то врезались, и можно заканчивать цикл, иначе мы будем двигаться дальше, пока не достигнем максимального числа итераций.

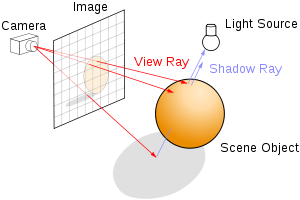
Мы могли бы каждый раз делать по очень маленькому шагу вдоль луча, но мы можем "шагать" более эффективно, используя алгоритм «трассировки сферами». Вместо того, чтобы на каждой итерации делать крошечный шаг, мы делаем максимальный возможный шаг. Этот максимально возможный шаг равен минимальному расстоянию из полученных (с помощью SDF) для каждого объекта на сцене.

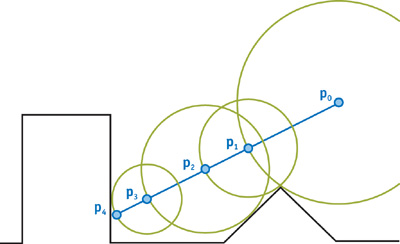
На рис. 7 - это камера. Синяя линия проходит вдоль направления луча, идущего от камеры через плоскость экрана. Первый сделанный шаг довольно большой, так как расстояние до ближайшей поверхности тоже велико. Поскольку точка на ближайшей поверхности не лежит на луче, мы продолжаем шагать до тех пор, пока в конце концов не столкнемся с поверхностью в точке

Реализованный на GLSL алгоритм марширования лучей выглядит так:

float depth = start;
for (int i = 0; i < MAX_MARCHING_STEPS; i++) {
    float dist = sceneSDF(eye + depth * viewRayDirection);
    if (dist < EPSILON) {
        // We're inside the scene surface!
        return depth;
    }
    // Move along the view ray
    depth += dist;

    if (depth >= end) {
        // Gone too far; give up
        return end;
    }
}
return end;

Если ты все сделал правильно, должно получиться что-то похожее:

Для того, чтобы сфера стала сферой, нам нужна модель освещения. Возьмем самую простую - освещение по Ламберту, для этого мы должны вычислить угол между источником света и нормалью к поверхности в точки пересечения луча взгляда и домножить цвет поверхности на величину этого угла. Для вычисления нормали к поверхности вспомним понятия градиента. Градиентом функции называется такой вектор:

Но для рендера в реальном времени мы не можем считать производные. Вместо того, чтобы брать действительную производную функции, мы будем считать ее аппроксимацию:

где - очень маленькая величина.

Умножая цвет сферы на величину угла между нормалью и источником освещения, мы получим:

Готово! Мы познакомились с базовыми инструментами трассировки лучей и смогли нарисовать объемную сферу. Во второй части моей статьи познакомимся с более сложной моделью освещения, тенями, и начнем изучать преломление света и понятие интерференции, которые нам пригодятся в рендере мыльного пузыря.

Исходный код фрагментного шейдера для плоского изображения

const int MAX_MARCHING_STEPS = 255;
const float MIN_DIST = 0.0001;
const float MAX_DIST = 100.0;
const float EPSILON = 0.0001;

float sphereSDF(vec3 samplePoint) {
    return length(samplePoint) - 1.0;
}

vec3 rayDirection(float fieldOfView, vec2 size, vec2 fragCoord) {
    vec2 xy = fragCoord - size / 2.0;
    float z = size.y / tan(radians(fieldOfView) / 2.0);
    return normalize(vec3(xy, -z));
}

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
	vec3 dir = rayDirection(45.0, iResolution.xy, fragCoord);
    vec3 eye = vec3(0.0, 0.0, 5.0);
    float dist = shortestDistanceToSurface(eye, dir, MIN_DIST, MAX_DIST);
    
    if (dist > MAX_DIST - EPSILON) {
        // Didn't hit anything
        fragColor = vec4(0.0, 0.0, 0.0, 0.0);
		return;
    }
    
    fragColor = vec4(1.0, 0.0, 0.0, 1.0);
}

Исходный код фрагментного шейдера для объемного изображения

const int MAX_MARCHING_STEPS = 255;
const float MIN_DIST = 0.0001;
const float MAX_DIST = 100.0;
const float EPSILON = 0.0001;

float sphereSDF(vec3 samplePoint) {
    return length(samplePoint) - 1.0;
}

float shortestDistanceToSurface(vec3 eye, vec3 marchingDirection, float start, float end) {
    float depth = start;
    for (int i = 0; i < MAX_MARCHING_STEPS; i++) {
        float dist = sceneSDF(eye + depth * marchingDirection);
        if (dist < EPSILON) {
			return depth;
        }
        depth += dist;
        if (depth >= end) {
            return end;
        }
    }
    return end;
}
            
vec3 rayDirection(float fieldOfView, vec2 size, vec2 fragCoord) {
    vec2 xy = fragCoord - size / 2.0;
    float z = size.y / tan(radians(fieldOfView) / 2.0);
    return normalize(vec3(xy, -z));
}

vec3 estimateNormal(vec3 p) {
    return normalize(vec3(
        sphereSDF(vec3(p.x + EPSILON, p.y, p.z)) - sphereSDF(vec3(p.x - EPSILON, p.y, p.z)),
        sphereSDF(vec3(p.x, p.y + EPSILON, p.z)) - sphereSDF(vec3(p.x, p.y - EPSILON, p.z)),
        sphereSDF(vec3(p.x, p.y, p.z  + EPSILON)) - sphereSDF(vec3(p.x, p.y, p.z - EPSILON))
    ));
}

vec3 lambertIllumination(vec3 p, vec3 lightPos) {
    
    vec3 lightVector = normalize(lightPos - p);
    vec3 n = estimateNormal(p);
    return vec3(1.0, 0.0, 0.0) * max(0.0, dot(n, lightVector));
}


void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
	vec3 dir = rayDirection(45.0, iResolution.xy, fragCoord);
    vec3 eye = vec3(0.0, 0.0, 5.0);
    float dist = shortestDistanceToSurface(eye, dir, MIN_DIST, MAX_DIST);
    
    if (dist > MAX_DIST - EPSILON) {
        // Didn't hit anything
        fragColor = vec4(0.0, 0.0, 0.0, 0.0);
		return;
    }
    
    // The closest point on the surface to the eyepoint along the view ray
    vec3 p = eye + dist * dir;
    
    vec3 color = lambertIllumination(p, vec3(3.0, 2.0, 4.0));
    
    fragColor = vec4(color, 1.0);
}