23.08.2022 09:00
Igorec_matveev 3 1100 Источник

Итак, вам нужно ускорить модель объекта управления в несколько раз. Вы попробовали рекуррентные сетки, а потом решили вспомнить Ляпунова и Понтрягина и сделать это без data science. Поехали!

Введение

В этом блоге мы уже выпустили серию статей про суррогатные модели, которыми можно заменять сложные технические системы. Была статья и про расчет системы управления приводом элерона самолета через рекуррентную нейросеть на ячейках GRU.

Сеть GRU продемонстрировала неплохие результаты по части ускорения выполнения исходной модели, но очень сильно ошибалась на промежутках с сильной осцилляцией и вообще при высокой динамике выходной величины. Вторая проблема, как всегда с нейросетями, была в экстраполяции: модель была очень чувствительна к предыстории (показаниям, которые предшествовали началу моделирования), а чем больше берешь предысторию, тем меньше данных остается в датасете.

Вот и мы поставили себе следующую цель: повысить качество моделирования выходной величины, заменив объект управления на алгоритм динамического регрессора.

Основные этапы работы

Рассмотрим систему управления приводом элерона самолета. Модель представлена рисунке 1 в виде функциональных блоков MATLAB/SIMULINK.

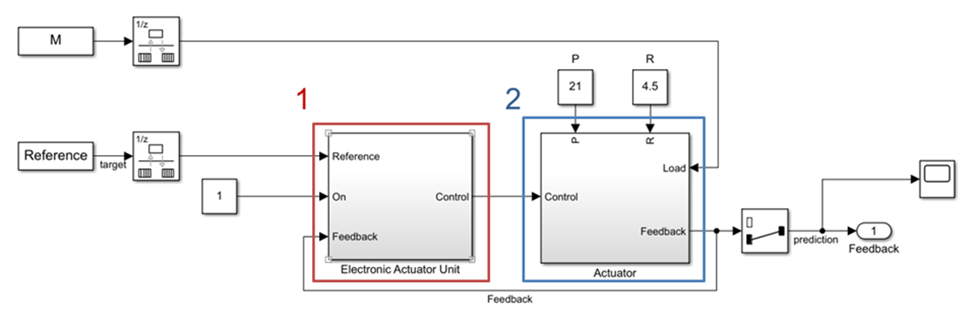
Рисунок 1 – Система управления приводом элерона самолета
Рисунок 1 – Система управления приводом элерона самолета

Слева находится блок управления, мы его не трогаем. Справа находится привод, который получает из внешнего мира реакцию на свои перемещения (момент сопротивления среды M) и, конечно, сигнал управления.

В этой работе мы заменим блок справа на DR (Dynamic Regressor) при помощи алгоритма идентификации параметров динамического объекта, который исходные авторы метода [1] упоминают в контексте адаптивных систем и бессенсорного управления.

В этих методах звено считается объектом с динамическими характеристиками, которые постоянно нужно пересчитывать. При этом это не простой фильтр входных данных типа сглаживания, а модель, которая должна научиться изменять свои характеристики самостоятельно, в зависимости от входных данных.

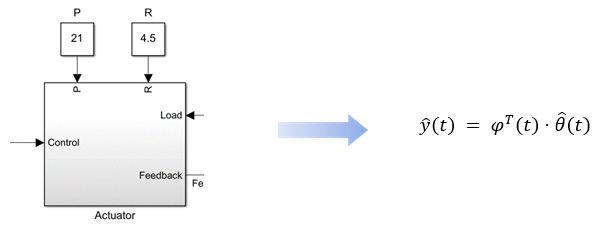
Рисунок 2 – Замена функционального блока системы на модель с динамической линейной регрессией
Рисунок 2 – Замена функционального блока системы на модель с динамической линейной регрессией

Итак, наш DR создан, чтобы заменить объект, заданный в виде дифференциальных уравнений с начальными условиями (форма Коши):

\dot y=f(y(t),u(t)), \qquad y(0)=0

где y(t) \in \mathbb{R}– вектор состояния системы;
u(t)\in \mathbb{R}^{n\times2}– вектор управления.

Замена на Dynamic Regressor:

\hat y(t) = \phi^T(t) \cdot \hat \theta(t)

где \hat y(t) \in \mathbb{R}– оценка выходной переменной (перемещение звена);
\hat \theta(t) \in \mathbb{R}^{5\times1}– вектор неизвестных параметров;
\phi(t) \in \mathbb{R}^{5 \times 1}– вектор входных сигналов или регрессор модели.

Вектор \phi(t) включает в себя управляющие сигналы с контроллера C_1(t), C_2(t)постоянные P, R, которые отвечают за режим работы привода и внешний суммарный момент сил M(t).

\phi(t)=col(M(t),C_1(t),C_2(t),P,R)

В задаче у нас известен сигнал управления «Reference», который управляемый объект должен отрабатывать, минимизируя отклонение между своим выходом и эталоном (считаем, что объект управления сделан правильно и имеет только отрицательную обратную связь).

e(t)=R(t)-y(t)\rightarrow0

где R(t) \in \mathbb{R}– референсный сигнал;
y(t) \in \mathbb{R}– выходная переменная объекта управления с ДУ.

В последнем уравнении выходной сигнал с объекта управления (который описывается дифференциальными уравнениями) y(t) заменяем на модель с динамическим регрессором \hat y(t).

Тогда ошибку можно переписать в следующем виде:

e(t)=R(t)-\hat y(t)=R(t) - \phi^T(t) \cdot \hat \theta(t) \rightarrow 0

Осталось только определить вектор неизвестных постоянных. Никакой магии, DR для этого использует градиентный метод оценивания параметров, в качестве функционала ошибки – квадратичный критерий. Вычислим оценки неизвестных параметров:

L(t)=\frac{1}{2}e^2(t) \rightarrow 0 \\ \\ \dot {\hat \theta} = -\gamma \nabla_\hat \theta L(t)=\gamma \cdot \phi(t) \cdot e(t) \\ \\ \dot {\hat \theta} =\gamma \cdot \phi(t) \cdot [y(t) - \phi^T(t) \cdot \hat \theta(t)] \\ \\ \hat \theta(t) = \int_{t_0}^{t} \dot{\hat\theta}(t) dt + \hat\theta(0)

В каждый момент времени формируется новый вектор оценок параметров линейной регрессии \hat\theta(t)и происходит адаптация под характер эталонного сигнала R(t).

Условия, при которых динамический регрессор выдает адекватную оценку параметров модели, важно учитывать при построении моделей. Для модели вида:

\hat y(t) = \phi^T(t) \cdot \hat \theta(t)

где y(t) \in \mathbb{R}, \phi(t) \in \mathbb{R}^{n \times 1}, \hat \theta(t) \in \mathbb{R}^{n\times1}

Вектор оценок \hat \theta(t)сходится к своим истинным значениям или ошибка e_\theta(t) параметров сходится к нулю асимптотически, если выполняется условие незатухающего возбуждения, которое накладывается на регрессор \phi(t):

\int_{t}^{t+T}\phi(\tau)\cdot\phi^T(\tau)d\tau \geq \rho I

где существуют такие положительные числа Tи \rho, для которых выполняется данное неравенство.

Теперь, к делу!

Моделирование показало практически одинаковые результаты по скорости вычисления искомой величины в сравнении с сетью GRU. Зато максимальная относительная ошибка составила 7% для всего времени моделирования! Как и ожидается, выход DR-модели в целом четко следует заданным входным командам:

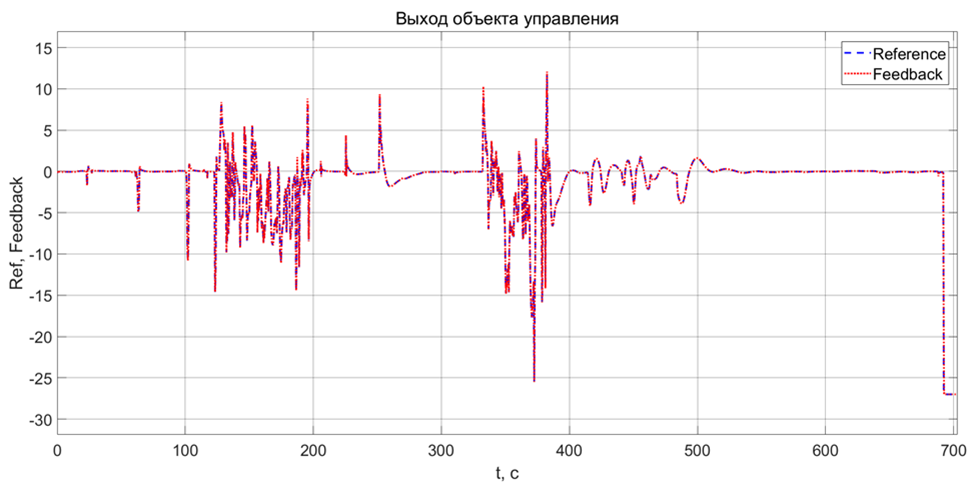
Рисунок 3 – Расчет величины перемещения звена привода элерона
Рисунок 3 – Расчет величины перемещения звена привода элерона

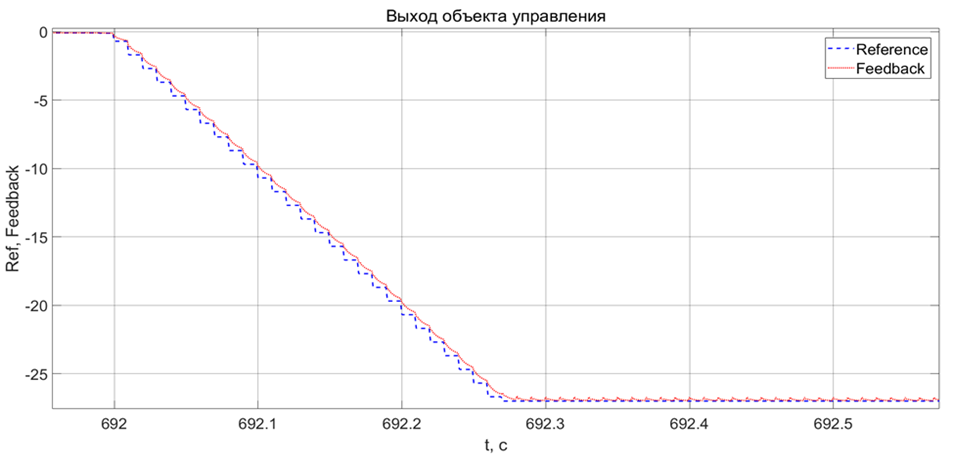
Если приблизиться, обратная связь по DR-модели очень плотно следует за сигналом управления – хорошо, тут ничего не нарушается.

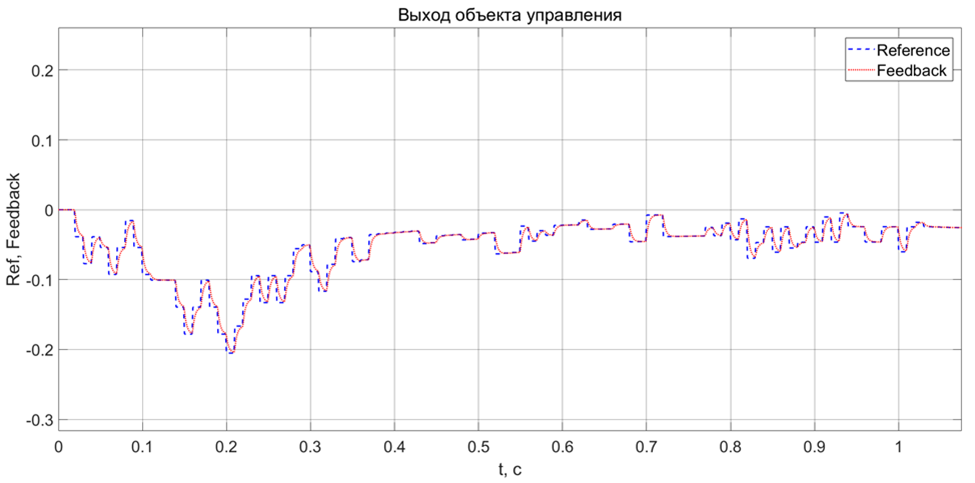
Рисунок 4 – Начальный момент времени моделирования
Рисунок 4 – Начальный момент времени моделирования

И напоследок сравним результаты на участках с сильной динамикой:

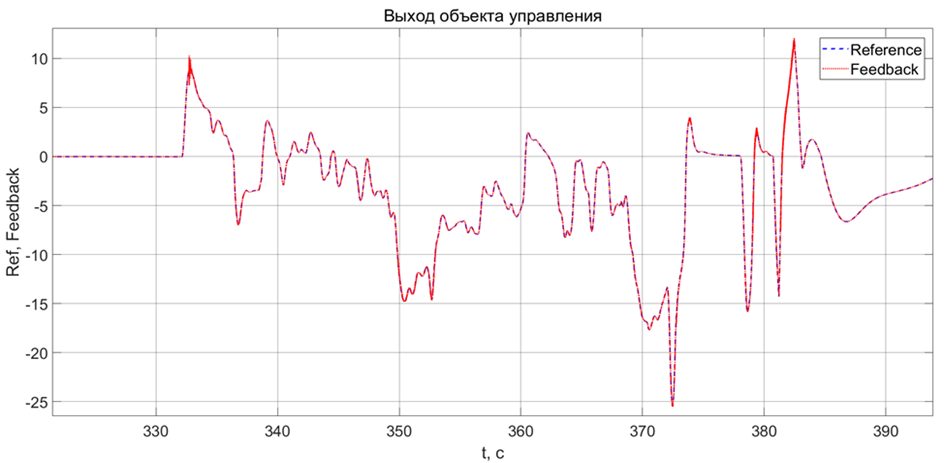
Рисунок 5 – Участок с сильной осцилляцией
Рисунок 5 – Участок с сильной осцилляцией

Как на участке с колебаниями, так и на участке с резким скачком, DR-модель отрабатывает нормально.

Рисунок 6 – Заключительный участок времени моделирования
Рисунок 6 – Заключительный участок времени моделирования

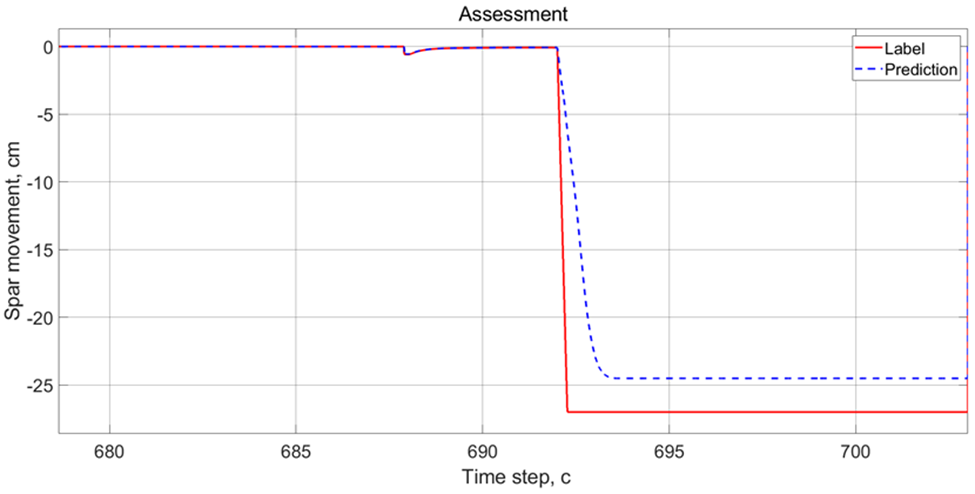
К слову, нейронная сеть тут допустила большую ошибку на заключительном этапе расчета, что ярко проиллюстрировано на рисунках 6 и 7.

Рисунок 7 – Заключительный участок времени моделирования с сетью GRU
Рисунок 7 – Заключительный участок времени моделирования с сетью GRU

Заключение

Система управления с динамическим регрессором показала гораздо лучшие результаты по моделированию величины перемещения звена привода элерона самолета, чем GRU-нейросеть.

Это доказывает, что инвестиции в изучение моделируемой системы позволяют выбрать такой метод, который будет работать гораздо лучше нейросетей.

Максимальная относительная ошибка составила 7%. Процесс расчета ускорен в 5 раз (7.34 сек вместо 36.6 сек). Преимущество разработанной методики заключается в онлайн-обучении или адаптации к новым оценкам параметров линейной модели в процессе моделирования.

Ссылки на полезные источники

Игорь Матвеев

Инженер, ЦИТМ Экспонента@Igorec_matveev

Николай Капырин

Инженер, ЦИТМ Экспонента @n_kapyrin

Комментарии (3)


  1. Arastas
    23.08.2022 11:21
    #24655796

    Приятно, что кто-то с Хабра читает АиТ, хотя и несколько неожиданно. ;)

    Вы в заключении пишете про расширенный регрессор. Вы его как-то расширяли?


    1. Igorec_matveev Автор
      23.08.2022 11:35
      #24655824
      +1

      Спасибо за замечание. Это была опечатка! В работе пока рассматривали применение динамического регрессора. В будущем, планируем провести эксперименты с расширением для ускорения сходимости :)


      1. Arastas
        23.08.2022 11:41
        #24655840

        Вы знаете, я не уверен, что термин «динамический регрессор» используется. Есть динамические регрессионные модели, есть динамическое расширение регрессора.