Задачник по теории информации + ML. Часть 2 / forpes.ru

11.09.2022 20:17

greck 0 1400 Источник

В части 1 мы познакомились с понятием энтропии.

В этой части я рассказываю про Взаимную Информацию (Mutual Information) – концепцию, которая открывает двери в помехоустойчивое кодирование, алгоритмы сжатия, а также даёт новый взгляд на задачи регрессии и Machine Learning.

Это необходимая компонента, чтобы в следующей части перейти к задачам ML как к задачам извлечения взаимной информации между факторами и прогнозируемой величиной. Один из способов объяснения успешности ML моделей заключается в том, что они создают естественное бутылочное горлышко, ограниченное автоподстраиваемым значением бит информации, через которое пропускается (дистиллируется) информация о входных данных. Но про это – в следующей части.

Здесь будет три важных картинки:

первая – про визуализацию энтропий двух случайных величин и их взаимную информацию;
вторая – про понимание самой концепции зависимости двух случайных величин и про то, что нулевая корреляция не значит независимость;
и третья – про то, что пропускная способность информационного канала имеет простую геометрическую интерпретацию через меру выпуклости функции энтропии.

Также мы докажем упрощённый вариант теоремы Шаннона-Хартли о максимальной пропускной способности канала с шумом.

Материал довольно сложный, изложен неподробно и больше похож на заметки для лектора. Подразумевается, что вы будете самостоятельно изучать непонятные моменты или писать мне вопросы, чтобы я раскрыл их понятнее и подробнее.

2. Mutual Information

Когда есть две зависимые величины, можно говорить о том, сколько информации об одной содержится в другой. Последние задачи в части 1 по сути были про это – про Взаимную Информацию двух случайных величин.

Рассмотрим, для примера, пару= (вес_человека, рост_человека). Для простоты будем считать, что это целые числа в килограммах и сантиметрах с конечным числом возможных значений. Теоретически, мы могли бы собрать данные 7 млрд. людей и построить двумерное распределение для пары — распределение двух зависимых случайных величин. Можно построить отдельно распределение только веса $\mathrm{Pr}(w=x)$ (забыв про рост), и распределение роста $\mathrm{Pr}(h=y)$ (забыв о существовании веса). Эти два распределения называются маржинальными распределениями для совместного распределения на плоскости

Эти маржинальные распределения естественно в данном контексте называть априорными распределениями — они соответствуют нашему знанию о весе и росте, когда мы ничего не знаем про человека.

Ясно, что информация о росте человека заставит нас пересмотреть распределение веса, например, сообщение "рост = 2 метра 10 см" сместит распределение веса в область больших значений. Новое распределение веса после получения сообщения естественно назвать апостериорным. Соответственно, можно записать формулу информации, полученной в этом сообщении, как разность энтропий априорного и апостериорного распределений:

$I_{w}(``h=2.10 ")=\\=H(\{\mathrm{Pr}(w=x)\}_x) - H(\{\mathrm{Pr}(w=x | h=2.10)\}_x)$

Здесь снаружи фигурных скобок я пишу индекс, по которому нужно "бежать" внутри фигурных скобок, чтобы получить список, а если индексов два, то матрицу.

Важно отметить, что никто не гарантирует, что эта величина будет положительная. Возможно такое совместное распределение при котором условное распределение $\{\mathrm{Pr}(w = x|h = 2.10)\}_x$ имеет большую энтропию (неопределенность), нежели маржинальное распределение $\{\mathrm{Pr}(w = x)\}_x$ . Но в среднем для зависимых случайных величин значение $I_{w}(``h=x")$ положительно, а именно, мат. ожидание этой величины положительно:

$M_{I_{w}(``h= \cdot")}=\sum_x \mathrm{Pr}(h=x) \cdot I_{w}(``h=x") \ge 0$

Эту величину естественно назвать информацией о величине в величине . Оказывается, она симметрична относительно перестановки в паре .

Опр. 2.1: Взаимная информация двух случайных величин – это

$\mathrm{MI}(w, h) = \sum_x \mathrm{Pr}(h=x) \cdot I_{w}(``h=x")$

или

$\mathrm{MI}(w, h) = \sum_x \mathrm{Pr}(w=y) \cdot I_{h}(``w=y")$

или

$\mathrm{MI}(w, h) = H(w) + H(h) - H(\{w,h\})$

Это три эквивалентных определения. $H(\{w,h\})$ — это энтропия дискретного распределения, у которого значения не числа, а пары чисел $\{y,x\}$ . Эквивалентность докажем ниже.

Есть визуализация того, чему равно значение MI:

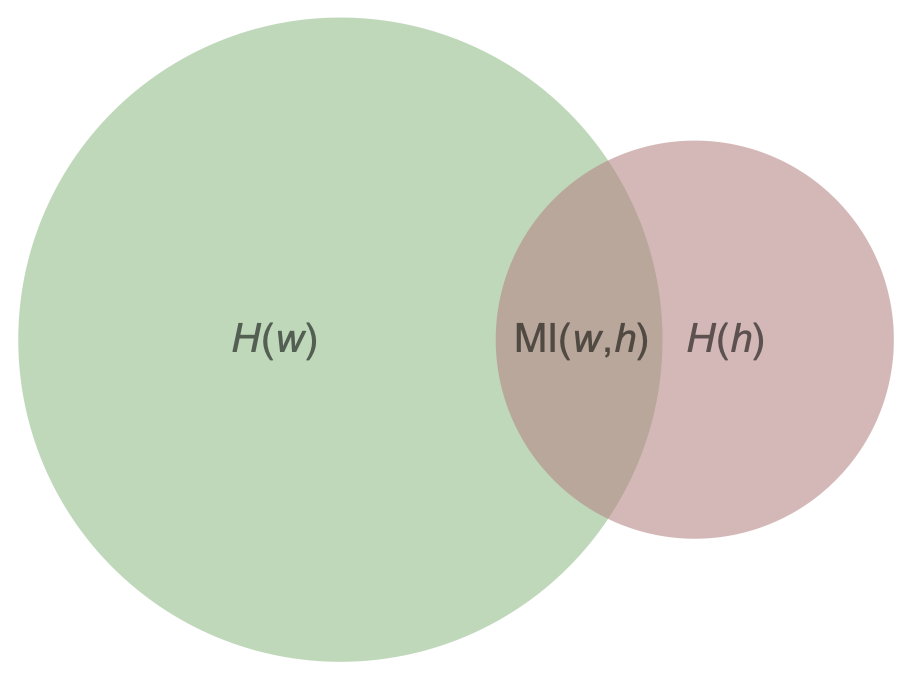
Энтропиям случайных величин соответствуют круги – зелёный и красноватый, их площади равны и , а коричневая площадь их пересечения как раз равна $\mathrm{MI}(w,h).$

Энтропия как мера

Эта визуализация, с одной стороны, не более чем визуализация, подчёркивающая, что энтропия – это неотрицательная величина, и что $\mathrm{MI}(w,h)$ тоже неотрицательная величина, которая меньше либо равна обеих энтропийи . Но, с другой стороны, есть интересные результаты, что можно построить пространство с мерой, в котором случайная величина соответствует подмножеству, объединение подмножеств соответствует прямому произведению случайных величин (то есть объединение в пару), а мера подмножеств и есть энтропия соответствующих случайных величин.

Распишем подробнее первое выражение:

$\mathrm{MI}(w, h) = \sum_x \mathrm{Pr}(h=x) \cdot I_{w}(``h=x")\\= \sum_x \mathrm{Pr}(h=x) \cdot ( H(\{\mathrm{Pr}(w=y)\}_y) - H(\{\mathrm{Pr}(w=y|h=x)\}_y)) \\ = H(\{\mathrm{Pr}(w=y)\}_y) - \sum_x \mathrm{Pr}(h=x) \cdot H(\{\mathrm{Pr}(w=y|h=x)\}_y)\\ = H(w) - H( w | h)$

Запись — это просто сокращение для

$\sum_x P(h=x) \cdot H(\{\mathrm{Pr}(w=y|h=x)\}_y)$
и называется условной энтропией.

Для независимых случайных величин

$I(``h=x") =\\= H({\mathrm{Pr}(w=y)}) - H({\mathrm{Pr}(w=y|h=x)})=0$

так как по определению независимости $\mathrm{Pr}(w=y) = \mathrm{Pr}(w=y | h=x)$ для любого а значит для независимых случайных величин взаимная информация равна 0.

Оказывается, в обратную сторону тоже верно, то есть утверждение $\mathrm{MI}(w, h) = 0$ эквивалентно независимости случайных величин. А вот для корреляции двух случайных величин аналогичное утверждение было бы неверным.

Чтобы увидеть эквивалентность определений MI, удобно ввести обозначения:

$P = \{ p_{x,y} \}_{x,y}$
— вероятности того, что рост и вес равны $(x,\; y)$ .
$R = \{ r_{x} \}_x = \{\sum_y p_{x,y}\}_x$
— вероятности того, что рост равен (маржинальное распределение роста).
$Q = \{ q_{y} \}_y = \{\sum_x p_{x,y}\}_y$
— вероятности того, что вес равен (маржинальное распределение веса).

Будем считать, что все эти числа не равны 0.

Во-первых, заметим, что $\mathrm{Pr}(w=y | h=x) = p_{x, y} / r_x.$

Далее делаем подстановки и простые преобразования и получаем эквивалентность первого и третьего определения:

$\mathrm{MI}(w, h) =\\=\sum_x \mathrm{Pr}(h=x) \cdot (H(\{q_y\}_y) - H(\{\mathrm{Pr}(w=y | h=x)\}_y ) = \\ \ \ = \sum_x r_x \cdot (H(Q) - \sum_y p_{x,y}/r_x \cdot \log (r_x/p_{x,y})) = \\ \ \ = H(Q) - \sum_{x,y} r_x \cdot (p_{x,y} / r_x) \cdot\log( r_x / p_{x,y}) = \\ \ \ = H(Q) - \sum_{x,y} p_{x,y} \log (r_x / p_{x,y}) = \\ \ \ = H(Q) + \sum_{x,y} p_{x,y} \log (1 / r_x) - \sum_{x,y} p_{x,y} \log (1 /p_{x,y}) = \\ \ \ = H(Q) + \sum_{x} r_x \log (1 / r_x) - \sum_{x,y} p_{x,y} \log (1/p_{x,y}) = \\ \ \ = H(Q) + H(R) - H(P)$

Рассмотрение случая, когда какие-то из вероятностей равны нулю оставим учебникам.

Задача 2.1: Приведите пример случайных величин, для которых корреляция равна нулю, а $\mathrm{MI}$ не равна нулю.

Задача 2.2: Две случайные величины много раз измерили и нанесли точки на плоскость. Какие картинки соответствуют зависимым случайным величинам, а какие – независимым?
Для каких из них корреляция x и y равна 0?

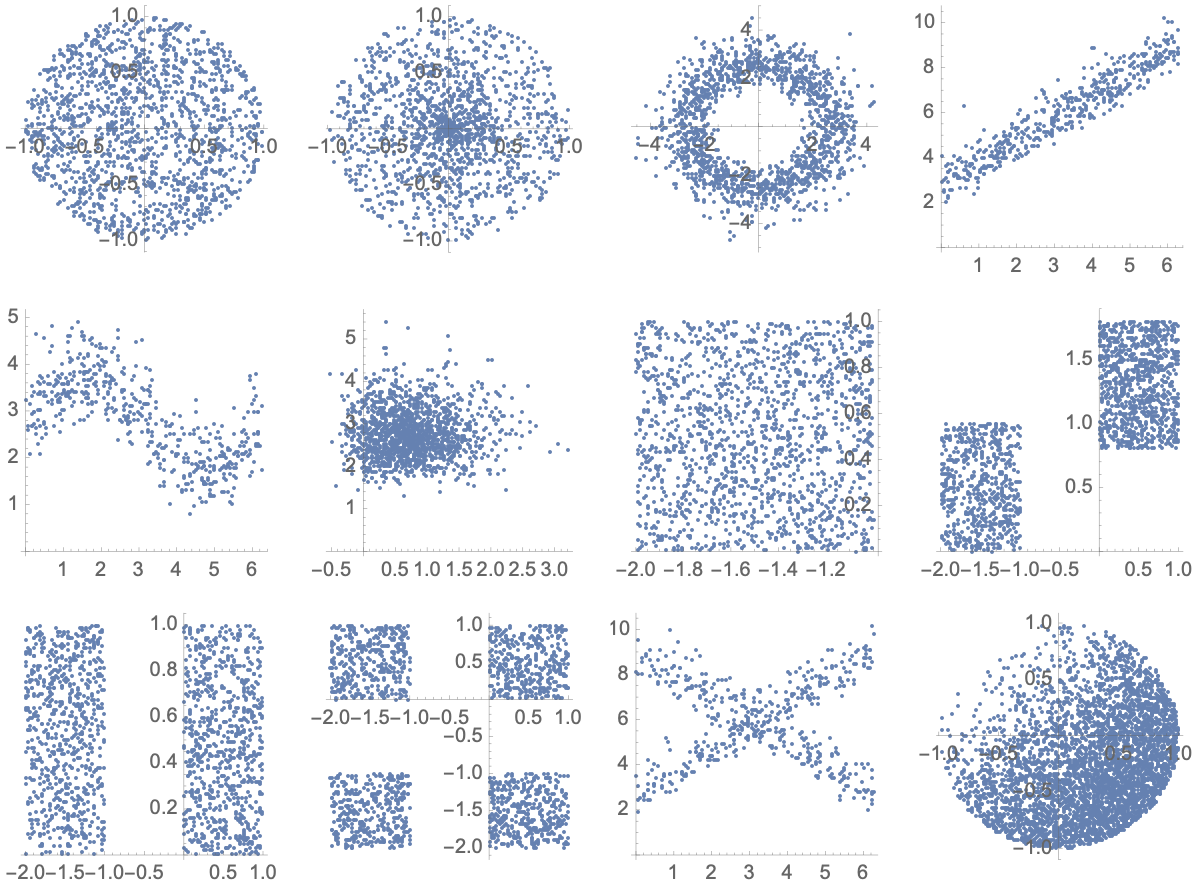
Результаты измерения двух случайных величин.
На каких из 12 картинок эти две величины зависимы? — Результаты измерения двух случайных величин. На каких из 12 картинок эти две величины зависимы?

Ответы

Зависимые: 3-й, 4-й, 5-й, 8-й, 11-й, 12-й.

Корреляция равна нулю для всех, кроме 4-го, 5-го, 8-го и 12-го.

Задача 2.3: Посчитайте MI(w="число делится на 6", h="число делится на 15"). Предполагается, что мы берём одно из натуральных чисел случайно и все числа равновероятны. Чтобы не мучатся с понятием равномерного распределения на натуральных числах, считайте, что мы случайно берём число из множества {1, ..., 30}.

Ответ

Мы знаем маржинальные распределения: $R= \{5/6, 1/6\}$ и $Q=\{14/15, 1/15\}.$ Кроме того, мы знаем что вероятность делится и на 6, и на 15 равна 1/30. Из этого выводится матрица совместных вероятностей:

$P = \|p_{xy}\| =\\=\left\|\begin{array}{cc} 5/6 - (1/15 - 1/30) & 1/6 - 1/30 \\ 1/15 - 1/30 & 1/30\end{array}\right\|=\\=\left\|\begin{array}{cc} 4/5 & 2/15\\ 1/30 & 1/30\end{array}\right\|$

Используем формулу $\mathrm{MI} = H(w) + H(h) - H({w,h})$ и получаем
MI=0.0311278

Задача 2.4: Докажите, что есть ещё одно эквивалентное определение

$\mathrm{MI}(w, h) = D_{KL}( \{\mathrm{Pr}(w = x, h = y)\}_{x,y}, \;\{\mathrm{Pr}(w=x) \cdot \mathrm{Pr}(h=y) \}_{x,y}),$

то есть MI – это то, насколько код Хаффмана для потока пар $\{w,h\},$ построенный в предположении независимости случайных величин (то есть в предположении, что совместное распределение равно произведению маржинальных), будет менее эффективен, чем код Хаффмана, построенный на настоящем совместном распределении. Измеряется в сэкономленных битах на символ (символ – измерение пары $\{w,h\}$ ).

Мы до сих пор жили в области дискретных распределений. Переход к непрерывным величинам получается просто.

Вспомним про задачу 1.7. Давайте предположим, что у нас есть вещественные случайные величины , но мы их дискретизировали — первую на корзинки размера $\varepsilon_1$ , а вторую — на корзинки размера $\varepsilon_2$ . Подставив в выражение

$H(\{q_y\}_y) + H(\{r_x\}_x) - H(\{p_{x,y}\}_{x,y})$

вместо H приближенную формулу (см. задачу 1.7)

$\log(1/\varepsilon) - \int_{-\infty}^{+\infty} \rho(x)\log(\rho(x))dx$

для энтропий дискретизированного непрерывного распределения, мы получим, что из первого слагаемого вылезет $\log(1/\varepsilon_1),$ из второго слагаемого — $\log(1/\varepsilon_2),$ а из третьего вычитаемого — $\log(1/(\varepsilon_1\cdot \varepsilon_2)$ и эти три кусочка сократятся.
Таким образом, взаимную информацию непрерывных величин естественно определить как предел MI дискретизированных случайных величин при стремлении к корзинкам нулевого размера.

Опр. 2.2: Взаимная информация двух непрерывных случайных величин равна

$\mathrm{MI}(h,w) = H(\rho_h) + H(\rho_w) - H(\rho_{(h,w)}).$

Здесь мы пользуемся H из определения 1.6 части 1.

Задача 2.5: Оцените $\mathrm{MI}(predict, target)$ для какой-либо имеющейся у вас задачи прогноза чего-либо. Посчитайте $\mathrm{MI}(predict, target) / H(target)$ , насколько близко это отношение к 1?

Задача оценки MI двух случайных величин по множеству их измерений по сути сводится к задаче расчета матрицы $\|p_{xy}\|$ совместного распределения для дискретизированных значений этих случайных величин. Чем больше корзинок в дискретизации, тем меньше неточность, связанная с этой дискретизацией, но тем меньше статистики для точной оценки $p_{xy}$ .

Оценка MI по наблюдаемым измерениям — отдельная большая тема, и мы к ней ещё вернёмся в задаче 3.1.

Задача 2.6: Докажите, что для любой строго монотонной функции верно, что $\mathrm{MI}(w,h) = \mathrm{MI}(f(w), h).$

Ответ

Пусть . Возьмём две формулы

$\mathrm{MI}(w, h) = H(h) - H(h | w) =\\= H(h) - \int (\rho(y) dy) H(h | w = y)$ $\mathrm{MI}(w_f, h) = H(h) - H(h | w_f) =\\= H(h) - \int (\rho_f(z) dz) H(h | w_f = z)$

Первые слагаемые просто совпадают, а вычитаемые равны, так как их физический смысл — это среднее значение , где — это разные случайные величины, получаемые из при фиксирования значения или, что то же самое при фиксировании значения . Усреднение происходит по распределению значений или, что, опять же, неважно.

Посмотрите на интегралы. Значения и просто совпадают, и в обоих формулах происходит усреднение этой величины по одной и той же вероятностной мере $\mu$ просто по-разному параметризованной: $d\mu = \rho(x) dx = \rho_f(z) dz$ .

Опр. 2.6: Информационный канал — это цепь Маркова длины 2, задающая зависимость между между двумя зависящими случайными величинами, одна из которых называется input, а другая — output. Часто под информационным каналом имеют в виду лишь матрицу переходных вероятностей: $T=\|t_{y,x}\|=\|\{\mathrm{Pr}(output = y | \; input = x)\}_{y,x}\|,$ без фиксирования значения входного распределения. Распределение на входе будем обозначать как вектор $R= \|\{r_x\}_x\|=\|\{\mathrm{Pr}(input=x)\}_x\|,$ а распределение значений на выходе как вектор $Q = \|\{q_y\}_y\|=\|\{\mathrm{Pr}(output=y)\}_y\|.$

Для дискретных распределений мы для каждого из M возможных входов имеем распределение на N возможных значениях выхода, то есть мы по сути имеем матрицу из M столбцов и N строчек, в которой все числа неотрицательные, а сумма чисел в каждом столбце равна 1.

Такие матрицы называются стохастическими матрицами, а точнее левыми стохастическими матрицами (left stochastic matrix).

Про левые и правые стохастические матрицы

У левых стохастических матриц сумма чисел в каждом столбце равна 1, а у правых – в каждой строчке. Бывают ещё дважды стохастические матрицы, в которых и столбцы и строчки суммируются в 1. Я выбрал вариант, когда вектор вероятностей значений на входе рассматривается как столбец, и чтобы получить вектор вероятностей значений на выходе нужно проделать обычное матричное умножение $Q = T \cdot R$ .

В англоязычной литературе вектор вероятностей принято рассматривать как строчку, матрицу переходов транспонировать (и она станет правой стохастической) и умножать на матрицу слева: $Q=R\cdot T$ . Я боюсь, это будет многим непривычно , поэтому выбрал вариант столбцов и левых стохастических матриц перехода.

Таким образом, информационный канал суть левая стохастическая матрица T. Задавая распределение $r_x = \mathrm{Pr}(input=x)$ на входе, вы получаете распределение $q_y = \mathrm{Pr}(output=y)$ на выходе, просто умножая матрицу $T= \|t_{y,x}\|$ на вектор :

$q_y = \sum_x t_{yx} \cdot r_x$

Пропускной способностью информационного канала называется максимальное значение $\mathrm{MI}(input, output)$ , достижимое на некотором распределении $R=\{r_x\}_x$ на входе.

Информационный канал для передачи бит, в котором 1 из-за помех превращается в 0 с вероятностью $\varepsilon_1,$ а 0 превращается в 1 c вероятностью $\varepsilon_0$ задается матрицей

$T = \left\|\begin{array}{cc} 1-\varepsilon_0 & \varepsilon_1\\ \varepsilon_0 & 1-\varepsilon_1 \end{array}\right\|$

Задача 2.7: Пусть есть информационный канал с помехами, в котором 1 превращается в 0 с вероятностью $\varepsilon_1,$ а 0 превращается в 1 c вероятностью $\varepsilon_0.$ Чему равно значение $\mathrm{MI}(input, \;output)$ при условии, что на вход поступает случайный бит с распределением $R=\{0.5, 0.5\}$ ? На каком распределении на входе достигается максимум $\mathrm{MI}(input, output)$ и чему он равен, то есть какая пропускная способность у этого канала?

Ответ:

Здесь удобно воспользоваться формулой

$\mathrm{MI} = H(Q) - \sum_x p_x \cdot H( \{\mathrm{Pr}(output = y | \; input = x)\}_y ).$

Имеем:

Распределение на входе:
$R = \{r_0, r_1\}$
Распределение на выходе:
$Q = \{q_0, q_1\} = \{r_0 \cdot (1 - \varepsilon_0) + r_1 \cdot \varepsilon_1, r_1 \cdot (1 - \varepsilon_1) + r_0 \cdot \varepsilon_0\}$
Совместное распределение, то есть распределение на парах (вход, выход): $P =\{\{r_0 \cdot (1 - \varepsilon_0), r_1 \cdot \varepsilon_1\}, \{r_1 \cdot (1 - \varepsilon_1), r_0 \cdot \varepsilon_0 \}\}$
И два условных распределения:
- $\{\mathrm{Pr}(output = y|\; input = 0)\}_y = \{1 - \varepsilon_0, \varepsilon_0 \},$
- $\{\mathrm{Pr}(output = y |\; input = 1)\}_y = \{\varepsilon_1, 1 - \varepsilon_1 \}.$

Если воспользоваться формулой MI, то получим:

$MI = H(Q) - r_0 \cdot H(\{1 - \varepsilon_0, \varepsilon_0 \}) - r_1\cdot H(\{\varepsilon_1, 1 - \varepsilon_1\})$

А эта формула не что иное как мера выпуклости функции (aka JSD, см. ниже) на отрезке $x \in [\varepsilon_1, 1 - \varepsilon_0]$ , а именно, это значение этой функции на выпуклой сумме абсцисс концов этого отрезка минус выпуклая сумма значений этой функции на концах отрезка (ординат отрезка).

На рисунке показана функция $f(x) = H(\{x, 1 -x \})$ . Отрезок KL делится точкой A в пропорции . Длина отрезка AB и есть значение MI.

Максимальная длина отрезка достигается в такой точке, в которой производная равна углу наклона отрезка.

Обобщая задачу 2.7 на многомерный случай, получаем:

Утверждение 2.1: Пропускная способность канала определяется мерой выпуклости функции $f(x) = H({x_1, x_2, \ldots, x_k})$ в симплексе, который является образом стохастического преобразования, задаваемым информационным каналом, а именно, максимальным значением разницы от афинной (aka выпуклой) суммы вершин симплекса и афинной суммы значений функции на вершинах симплекса. Максимум берётся по всем возможным весам, задающих афинную сумму.

Интересно, что на значение пропускной способности канала можно посмотреть как на некоторую меру объема, заключённого в симплексе, задаваемом множеством условных распределений как вершинами.

Опр. 2.4: Пусть есть несколько распределений ${P_1, P_2, \ldots, P_n}$ на одном и том же множестве значений. Дивергенция Шаннона-Джейсона (Jensen–Shannon Divergence, JSD) этого набора c весами $\{\pi_1, \ldots, \pi_n\}$ вычисляется как $\mathrm{MI}(input, output)$ для

$R=\{\pi_1, \ldots,\pi_n\}, \\ T=\|P_1,P_2,\ldots, P_n\|$

то есть

${\rm JSD}_{\pi_1, \ldots, \pi_n}(P_1, P_2, \ldots, P_n) =\\= H\left(\sum_{i=1}^n \pi_i P_i\right) - \sum_{i=1}^n \pi_i H(P_i).$

Чем сильнее распределения отличаются друг от друга, тем больше JSD. Максимум

$\max_{\pi_1, \ldots, \pi_n} {\rm JSD}{\pi_1, \ldots, \pi_n}(P_1, P_2, \ldots, P_n) = C(T)$

и есть пропускная способность канала $T=\|P_1,P_2,\ldots, P_n\|.$

Задача 2.8: Пусть есть две зависимые нормальные величины , с дисперсиями $\sigma_w^2$ и $\sigma_h^2$ соответственно, и пусть первая получается из второй добавлением независимого нормального шума c дисперсией $\sigma^2_n$ : Тогда $\sigma_w^2 = \sigma_h^2 + \sigma_n^2.$ Чему равна взаимная информация $\mathrm{MI}(w, h)$ ?

Ответ

Энтропии величин и равны

${1 \over 2}\cdot (1+\log(2\pi (\sigma_h^2 + \sigma_n^2))\\\;\;\;\mathrm{ и } \;\;\;\;{1 \over 2}\cdot (1+\log(2\pi \sigma_h^2))$

Энтропия пары вещественных случайных величин $\{w,h\}$ равна

$H(\rho_{(w,h)})={1\over 2}(1 + \log(2\pi \sigma_h^2)) + {1\over 2}(1 + \log(2\pi \sigma_n^2))$

Последнее равно после сумме энтропий двумерного распределения пары $\{h,noise\}$ (энтропия пары независимых равна сумме их энтропий). А энтропия пары $\{h, w\}=\{h,h+noise\}$ равна энтропии пары $\{h,noise\},$ потому что линейное преобразование вектора случайных величин даёт вектор с той же энтропией (докажите это!).

Поэтому по формуле $\mathrm{MI}(h,w) = H(\rho_h) + H(\rho_w) - H(\rho_{(h,w)})$ мы получаем

$\mathrm{MI}(w, h) = {1 \over 2}\log(1+ {\sigma_h^2 \over \sigma_n^2})$

Замечание 1: Когда дисперсия (мощность) шума равна дисперсии (мощности) сигнала каждое измерение содержит 0.5 бита информации о значении

Замечание 2: Собственно, этот результат и есть теорема Шаннона-Хартли в упрощённом виде.

Задача 2.9: Пусть есть две зависимые величины , где имеет экспоненциальное распределение с параметром $\lambda$ , а $h_k = \mathrm{floor}(k \cdot w) / k$ . Чему равна взаимная информация $\mathrm{MI}(w, h_k)$ ? Другими словами, сколько информации сохраняется при округлении экспоненциальной случайной величины до какого-то знака. Сравните $\mathrm{MI}(w, h_{10})$ и $\mathrm{MI}(w, h_{100}).$

Ответ

Задача на понимание. Из первой случайной величины однозначно определяется значение второй. Значит информация MI равна просто энтропии второй величины, то есть $H(\lambda^{1/k})/(1 - \lambda^{1/k})$ .

Задача 2.10: Пусть есть две зависимые величины , где имеет бета-распределение с параметрами $(\alpha,\;\beta)$ , а сэмплируется из биномиального распределения с параметрами . Чему равна взаимная информация $\mathrm{MI}(w, h_k)$ ? Другими словами, сколько бит информации про истинный CTR рекламного объявления можно извлечь в среднем из статистики кликов на k показах.

Задача 2.11: Две зависимые величины получаются следующим образом – сначала сэмплируется случайная величина $\lambda$ из экспоненциального распределения со средним $\lambda_0$ , а потом сэмплируются две пуассоновские случайные величины с параметром $\lambda$ . Чему равна взаимная информация $\mathrm{MI}(w, h)$ ? Одна из возможных интерпретаций этой задачи такая: чему равна взаимная информация между числом продаж в одну неделю и числом продаж в другую неделю некого неизвестного нам товара.

Последние задачи являются примером того, как зависимости случайных величин можно моделировать с помощью графических вероятностных моделей, в частности, байесовских сетей.

Задача 2.12: Случайная величина получается из независимых случайных величин $\{f_1,\ldots, f_n,\; noise\}$ с распределением $\mathcal{N}(0,1)$ по формуле

$target=\sum_i w_i\cdot f_i+w_{noise}\cdot noise$

Константные веса $\{w_1,\ldots,w_n\}$ вам неизвестны, но априорное знание о них, это то, что они независимо были сэплированы из $\mathcal{N}(0,1)$ . Вы решаете задачу вычисления оценок весов $\{\hat{w_i}\}_i$ классическим методом регрессии и строите прогноз

$predict = \sum_i \hat{w_i}\cdot f_i$

Как будет расти квадратичная ошибка $mse = M_{(target - predict)^2}$ и значение $\mathrm{MI}(predict, target)$ с ростом размера обучающего пула? Проанализируйте ответ для случая $w_{noise}=0$ .

Задачник по теории информации + ML. Часть 2 +4

2. Mutual Information

Комментарии (0)