Суффиксное дерево (Suffix Tree, ST) – это структура данных, которая позволяет "проиндексировать" строку за линейное время от её длины, чтобы потом быстро находить подстроки (за время О(длина искомой подстроки)).

Тема построения ST и его применения хорошо раскрыта в интернет (википедия, статья на хабр про алгоритм Вейнера, язык Си, и статья на хабр про алгоритм Укконена).
Но всегда есть соблазн поучаствовать в соревновании "написать проще и яснее", хотя шансов мало. Тем не менее, рискну.

Соблазн возникает в связи со следующими моментами:

• В наступившем мире больших данных соверешенно непонятно, как бы мы жили без линейных алгоритмов поиска похожих кусочков в гигабайтах данных (поиск строк в текстах, расшифровка ДНК, антиплагиат, алгоритмы сжатия за счет выявления повторений и др.). Suffix Tree и Suffix Array – главные структуры данных, позволяющие решать все эти задачи.

• ST по праву считается сложной структурой данных. Если в институте на экзамене вас спрашивают линейный алгоритм построения ST, есть серьёзные основания считать, что вас валят.

• Несмотря на сложность, алгоритм построения ST умещается в 35 строк на python (см. ниже метод _build_tree). Их буквально можно выучить и воспроизводить по памяти как некое произведение искусства, как воплощенный в набор символов труд человеческой мысли, причём не одного человека, и первые из них точно гении. :) Есть соблазн, всматриваясь в код, прикоснуться к великому и чему-то научиться.

Первый линейный алгоритм построения ST относится к 1973 году, но новые алгоритмы и варианты улучшения продолжали всё это время появляться:

• Weiner, 1973 – первый линейный алгоритм построения ST от последнего символа к первому.

• Ukkonen's algorithm, 1995 – первый простой алгоритм от первого символа к последнему, который позволяет строить дерево в режиме онлайн (когда символы берутся последовательно из некоторого потока).

• Farach, 1997 – Optimal suffix tree construction with large alphabets – эффективный алгоритм для алфавитов любой длины (в оценке времени работы отсутствует длина алфавита).

• Dany Breslauer, Giuseppe F. Italiano, 2011 – Near real-time suffix tree construction – эффективный онлайн алгоритм, который работает в среднем больше, чем Ukkonen's algorithm, а именно, вместо , где – длина текста, но зато и среднее, и худшее худшее время обработки одного символа равно, а у Ukkonen's algorithm на обработку одного символа может уйти время .

Что такое суффиксное дерево

Возьмём текст "abrakadabra".

Множество суффиксов этого текста – это строки

abrakadabra
brakadabra
rakadabra
akadabra
kadabra
adabra
dabra
abra
bra
ra
a

Их можно переупорядочить так, чтобы произошло максимальное количество "склеек" соседних строк по первым символам:

Например, так

abrakadabra
abra
adabra
akadabra
a
brakadabra
bra
rakadabra
ra
kadabra
dabra

В результате склейки одинаковых соседних по вертикали символов получается такое дерево:

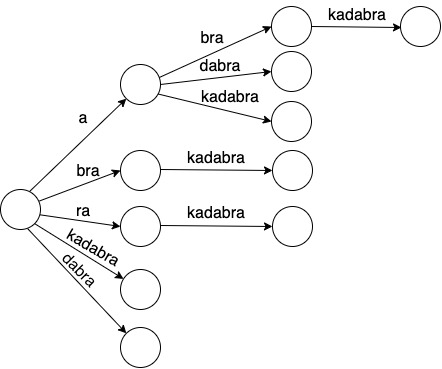
Это и есть суффиксное дерево: дерево, у которого есть выделенная вершина – корень (самая левая вершина), и у которого на рёбрах написаны подстроки исходного текста. Любой путь от корня до какой-либо вершины соответствует строке, которая получается соединением строк, написаных на рёбрах. Любой суффикс таким образом можно "прочитать" от корня дерева и оказаться в вершине. Но обратное неверно, не все внутренние вершины дерева соответствуют какому-то суффиксу, так как некоторые вершины появляются просто как необходимость разветвить разные суффиксы. На этом дереве таких примеров нет. Но попробуйте построить дерево для "abac". В нём будет внутренняя вершина, соответствующая строке "a", которая не является суффиксом.

Пути "ra-kadabra" и "bra-kadabra" можно каждый "схлопнуть" в одно ребро, и говорить про виртуальную вершину внутри ребра, в которой хранится суффикс.

Есть замечательная визуализация процесса построения суффиксного дерева "от первого символа к последнему", она соответствует наивному алгоритму последовательного добавления суффиксов в порядке уменьшения длины.

Наивный алгоритм построения суффиксного дерева

Можно представить себе такой алгоритм построения этого дерева. Сначала мы имеем просто один узел – корень. Потом, на шаге 1, добавляем в дерево слово abrakadabra. Появляется ребро с этим словом и ещё один узел. На втором шаге добавляем второй по длине суффикс brakadabra, а на шаге 3 – суффикс rakadabra. Интересное начинается на шаге 4: при добавлении суффикса akadabra мы видим, что у нас уже есть ребро, начинающееся на букву 'а', поэтому мы "пойдём" по нему и разветвим его в нужной точке.

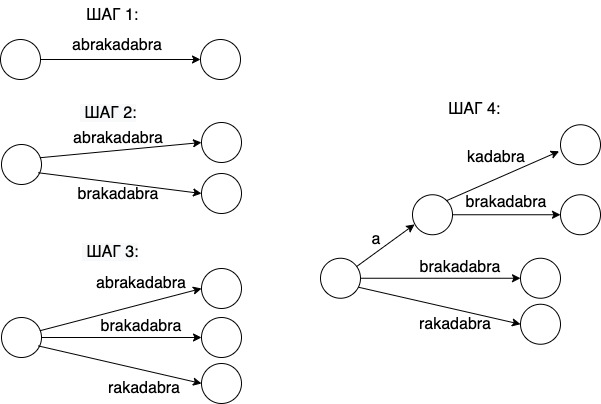
Так мы будем поступать, добавляя оставшиеся суффиксы, и получим дерево, показанное на первом рисунке (проделайте это полезное упражнение, ещё раз см. визуализацию).

Описанный наивный алгоритм конструирования суффиксного дерева не самый эффективный. Отдельный шаг для текста длины n может потратить время порядка n, самих шагов тоже n, поэтому грубая оценка даёт оценку. Но место, которое необходимо для хранения суффиксного дерева, оценивается как. Это просто понять, если заметить, что на каждом шаге (добавление ещё одного суффикса) наивного алгоритма появляется ребро и узел или не появляется. Место, которое тратится на каждое ребро – это просто два индекса начала и конца соответствующей подстроки текста.

То, что дерево занимает место, даёт надежду на то, что есть линейный алгоритм его построения. Удивительно, что такой алгоритм есть, мы разберём Укконена, но для начала расскажем, зачем нужно суффиксное дерево.

Применение суффиксного дерева

ST не только содержит все суффиксы, оно содержит все подстроки. И чтобы проверить, содержит ли text подстроку x, достаточно просто попробовать "прочитать" текст x, двигаясь от корня по рёбрам, и если это удаётся, то значит x является подстрокой.

С помощью суффиксного дерева можно за линейное время решать такие задачи:

Задача 1: Проверить, есть ли подстрока x в тексте text.

Задача 2: Найти наибольшую общую подстроку в текстах text1 и text2.

Задача 3: Найти самую длинную подстроку, которая встречается в тексте text более k раз.

Задача 4: Найти подстроку длины k, которая встречается максимальное количество раз.

Задача 5: Найдите в тексте топ 10 по частоте слов длины k или больше.

Задача 6: Найти в тексте text подстроку, которая подходит под регулярное выражение x, в котором есть один символ '*', соответствующий любой строке, в том числе пустой.

Задача 7: Дана база правильных слов. Напишите быструю функцию от аргумента word, исправляющую в слове word одну или две опечатки типа "замена одной буквы на другу", "удалена одна буква", "вставлена одна лишняя буква". Функция должна предлагать 10 вариантов для исправления опечаток, если входное слово word неправильное. Для того, чтобы функция работала быстро, можно и нужно построить некоторую структуру данных на базе правильных слов.

Задачи как бы простые, но сложность заключается в умении решать их за линейное время от размера входных данных. Все они могут быть решены с помощью ST. Используются идеи типа

• хранить в узлах какие-то дополнительные данные (например, глубину узла в символах, или количество листьев в поддереве);

• перед построением дерева добавлять в конец текста специальный уникальный символ $;

• для множества слов можно построить ST для текста, который получается соединением всех слов в один текст через специальный разделительный символ $.

Линейный алгоритм построения суффиксного дерева

Суть алгоритма buld_tree в том, что последовательно строится дерево для текстов "a*", "ab*", "abr*", "abra*", "abrak*", ... , где звёздочка * означает "все остальные слипшиеся символы". Состояние алгоритма определяется активной точкой:

• n – номер нового символа перед звёздочкой * , который мы хотим учесть и, как-бы, оторвать от звёздочки (сорри, раньше n было равно длине текста, теперь это индекс обрабатываемой буквы) и модифицировать соответствующим образом дерево;

• node – узел из которого мы шагаем в данный момент;

• edge – ребро, по которому мы шагаем; определяется парой индексов (first, last) и соответствует подстроке text[first: last];

• i – индекс внутри [first, last], который задаёт позицию на ребре, где именно мы находимся.

Есть ещё скрытый индекс j, такой, что текст text[j: first-1] как раз привёл бы нас из корня дерева в вершину node. Будем этот факт условно записывать в виде равенства
node = Node(text[j:first-1]).

В методе build_tree(node, n) внутри цикла while мы как бы находимся в режиме наивного алгоритма добавления некого суффикса text[j:end] в дерево и модифицируем дерево по мере необходимости. 

В данный момент мы прочитали от корня текст text[j:n] и хотим двигаться дальше, а именно, хотим прочитать очередной символ text[n+1] на ребре edge. Для этого увеличиваем на 1 переменные n и i и проверяем, верно ли, что text[i] == text[n], и если верно, то двигаемся по ребру дальше. В какой-то момент движение по ребру обрывается, например, новый символ не тот: text[i] != text[n]. И тогда мы должны врезать в ребро (в активную точку) новый узел и ответвиться от него продолжением text[n: end].

И вот сложный момент: когда мы, по мере необходимости, создаём новый узел new_node=Node(text[j:n]), мы делаем ещё рекурсивный вызов – отвлекаемся на подзадачу "пройти путь text[first:n] из узла Node(text[j+1:first-1]) и там тоже, если нужно, создать новый узел и вернуть ссылку на него". 

Ещё раз: двигаясь текстом text[n-k: n] из node=Node(text[j:first-1]) по ребру text[first:last] и встретившись с необходимостью создать новый узел new_node=Node(text[j:n]), мы понимаем, что аналогичная необходимость может ждать нас на пути из suff_node=Node(text[j+1:first-1]), если мы пойдём из него тем же текстом text[n-k: n]. И мы делаем рекурсивный вызов для решения этой подзадачи. При решении этой подзадачи, в свою очередь, также может случится рекурсивный вызов для решения подзадачи уже для узла Node(text[j+2: first-1]) и так далее.

Важная оптимизация – давайте в узлах Node(text[j:x]) создавать и хранить ссылки на узлы Node(text[j+1:x]). Назовём такие ссылки суффиксными ссылками. Это позволит нам не тратить время на поиск узла Node(text[j+1:x]) для рекурсивного вызова. Делая рекурсивный вызов, полезно также передать количество проработанных первых символов в тексте text[n-k:n], которые уже должны уметь читаться из узла Node(text[j+1:x]) (то есть для них должен быть путь из вершины Node(text[j+1:x])). Этот аргумент называется в коде skip.

Далее предлагаю просто помедитировать на код, который, в отличие от описаний на русском языке, однозначный и полный.

from collections import defaultdict
from typing import Optional


class Node:
    text = ""  # for debug purpose

    def __init__(self, edges=None, suff_link=None, parent=None):
        self.edges = edges if edges is not None else defaultdict(type(None))
        self.suff_link: Optional[Node] = suff_link
        self.parent: Optional[Node] = parent

    def __str__(self):
        if self.parent:
            idxs = [e.idxs for e in self.parent.edges.values() if e.target_node == self][0]
            return f"{self.parent}{self.text[idxs[0]: idxs[1]]}_"
        else:
            return "_"


class Edge:
    def __init__(self, idxs=None, target_node=None):
        self.idxs = idxs
        self.target_node: Optional[Node] = target_node


class SuffixTree:
    # node =  < suffix_link, parent, edges >
    # edges = { first_char => edge }
    # edge =  < idxs, target_node >
    # idxs = (first, last) # corresponds to label = text[first: last]
    def __init__(self, text):
        self.text = text
        self.joker_edge = Edge(idxs=(0, 1))
        self.joker = Node(edges=defaultdict(lambda: self.joker_edge))
        self.root = Node(suff_link=self.joker)
        self.joker_edge.target_node = self.root
        self.infty = len(self.text)
        self._build_tree(self.root, 0, self.infty)

    def __str__(self):
        return f"SuffixTree(text='{self.text}')"

    def pp(self, node=None, indent=0):
        node = node or self.root
        space = "    " * indent
        print(space + f"ID    : {node}")
        print(space + f"link  : {node.suff_link}")
        print(space + f"edges : ")

        for c, edge in node.edges.items():
            print(space + f"  -{c} {edge.idxs}={self.text[edge.idxs[0]: edge.idxs[1]]}:")
            self.pp(edge.target_node, indent + 1)

    def _build_tree(self, node: Node, n: int, infty: int, skip: int = 0):
        while n < infty:
            c = self.text[n]
            edge = node.edges[c]
            if edge is not None:
                first, last = edge.idxs
                i, n0 = first, n
                if skip > 0:
                    can_skip = min(skip, last - first)
                    i += can_skip
                    n += can_skip
                    skip -= can_skip

                while (
                    i < last and n < infty and
                    (self.text[i] == self.text[n] or edge is self.joker_edge)
                ):
                    i += 1
                    n += 1

                if i == last:  # go to the next node
                    node = edge.target_node
                else:  # splitting edge
                    middle_node = Node(parent=node)
                    middle_node.edges[self.text[i]] = edge
                    node.edges[c] = Edge(idxs=(first, i), target_node=middle_node)
                    edge.idxs = (i, edge.idxs[1])
                    edge.target_node.parent = middle_node
                    middle_node.suff_link = self._build_tree(node.suff_link, n0, n, i - first)
                    node = middle_node
            else:  # no way to go; creating new leaf
                new_leaf = Node(parent=node)
                node.edges[c] = Edge(idxs=(n, self.infty), target_node=new_leaf)
                node = node.suff_link
        return node


text = "abrakadabra"
Node.text = text
tree = SuffixTree(text)

tree.pp()

ID    : _
link  : _
edges : 
  -a (0, 1)=a:
    ID    : _a_
    link  : _
    edges : 
      -b (1, 4)=bra:
        ID    : _a_bra_
        link  : _bra_
        edges : 
          -k (4, 11)=kadabra:
            ID    : _a_bra_kadabra_
            link  : None
            edges : 
      -k (4, 11)=kadabra:
        ID    : _a_kadabra_
        link  : None
        edges : 
      -d (6, 11)=dabra:
        ID    : _a_dabra_
        link  : None
        edges : 
  -b (1, 4)=bra:
    ID    : _bra_
    link  : _ra_
    edges : 
      -k (4, 11)=kadabra:
        ID    : _bra_kadabra_
        link  : None
        edges : 
  -r (2, 4)=ra:
    ID    : _ra_
    link  : _a_
    edges : 
      -k (4, 11)=kadabra:
        ID    : _ra_kadabra_
        link  : None
        edges : 
  -k (4, 11)=kadabra:
    ID    : _kadabra_
    link  : None
    edges : 
  -d (6, 11)=dabra:
    ID    : _dabra_
    link  : None
    edges :

Не все суффиксные ссылки создаются, они создаются по мере необходимости. На картинке ниже пунктиром показаны две такие ссылки:

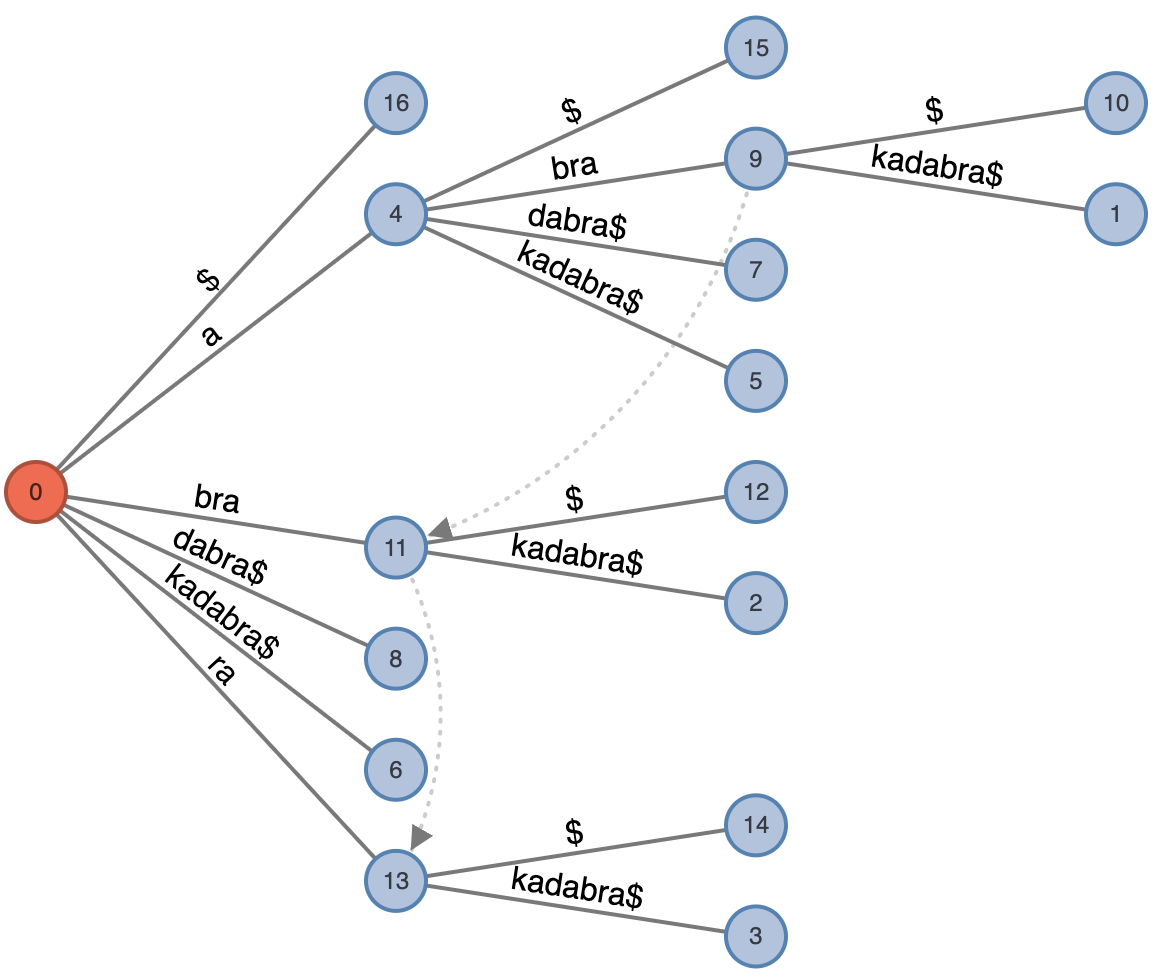
У меня будет очень оригинальное объяснение, почему алгоритм работает линейное время. В визуализации алгоритма буквы имеют три цвета:

• белый – недобавленные буквы, то есть буквы, слипшиеся в звёздочку; самой первой белой буквой мы можем как раз заниматься в данный момент;

• зеленый – буквы, которым соответствуют начала суффиксов, которые ещё предстоит добавить;

• голубой – буквы, для которых суффиксы уже добавлены (пусть со звёздочкой на конце).

На каждое нажатие кнопки Next алгоритм тратит время (задача для самостоятельного решения). Таких нажатий будет не более, чем 2 * len(text), так как каждое нажатие – это либо закрашивание буквы в зелёный или голубой цвет или перекрашивание зелёной буквы в голубой.

Моя статья про краткость. :) Если вам нужно подробнее и точнее, то читайте ответ на stackoverflow.

Про Suffix Array

Выше мы начали разговор с массива суффиксов:

abrakadabra"
"abra"
"adabra"
"akadabra"
"a"
"brakadabra"
"bra"
"dabra"
"kadabra"
"rakadabra"
"ra"

Отсортированный массив суффиксов (каждый суффикс – это просто индекс его начала), называется суффиксным массивом (Suffix Array). Как получить такой массив? Попытка решить задачу в лоб, вызвав метод sort, даст квадратичный алгоритм в худшем случае, а точнее . Действительно, количество операций сравнения оценивается как , а каждое сравнение в худшем случае даёт , например, когда текст состоит из повторений одного символа.

Тем не менее, есть алгоритм, который сортирует индексы суффиксов за линейное время – и это хорошая тема для следующей статьи. Одна из простых идей (но не работающих) – обычный рекурсивный алгоритм QuickSort, только в рекурсивном вызове нужно передавать длину общего префикса у всех строк в сортируемом подмассиве. Suffix Array проще для понимания, в нём можно делать привычный поиск методом деления пополам (но нужна mlr-оптимизация), и ещё из Suffix Array можно за линейное время построить ST, и это даёт ещё один алгоритм построения ST за линейное время.