
Истоки понятия «лабиринт»
Первое упоминание термина “maze” датируется тринадцатым веком, а “labyrinth” — к четырнадцатым. Сама концепция лабиринтов восходит к эпохе греческого мифологического героя Тесея — древнего героя, успешно прошедшего Кносский лабиринт и сразившего Минотавра.
Однако в более современном контексте лабиринты не имеют ничего общего с убийством мифологических существ. Теперь лабиринты чаще всего представляют из себя прямоугольную головоломку, состоящую из коридоров и поворотов, которые в конечном итоге ведут к выходу. И точно так же, как древний герой Тесей путешествовал по лабиринту, чтобы сразить Минотавра, современный человек решает задачу поиска пути в лабиринте не только для того, чтобы найти выход из лабиринта, но и для гораздо более широкого круга целей — решения связанных задач наиболее эффективным и доступным образом.
Введение
Лабиринты являются неотъемлемой частью нашей реальности. Хотя лабиринты в реальном физическом мире редко походят на стереотипное описание лабиринтов (черно-белая прямоугольная головоломка), общая идея и концепция лабиринтов находят свое отражение во многих аспектах нашего быта. В нашей повседневной жизни мы часто сталкиваемся с ситуациями, в которых необходимо найти самый быстрый и эффективный маршрут к заданному пункту назначения. Например, когда мы ищем в продуктовом магазине отдел с молоком, мы можем просто просмотреть каждый отдел, пока мы не найдем молоко. Однако это не самый эффективный способ. Если воспользоваться подсказками в магазине или полученными ранее воспоминаниями о том, куда ведут разные пути в магазине, поиск молока может стать гораздо более эффективным процессом. В некотором смысле мы должны использовать этот же процесс при решении задачи поиска пути в реальных лабиринтах. Метод/алгоритм, выбранный нами для поиска решения лабиринта, влияет на эффективность процесса.
Эффективность
Эффективность вычислительного алгоритма — это количество вычислительных ресурсов, используемых указанным алгоритмом, и время, необходимое для получения желаемого результата. Можно повысить эффективность алгоритма, удалив вложенные циклы for, кэшируя промежуточные или предыдущие результаты и уменьшив временную сложность алгоритма.
Временная сложность
Временная сложность измеряет время выполнения каждого оператора в коде алгоритма. При анализе фрагмента кода на предмет его временной сложности используется нотация большого “O”. Временная сложность — это функция от размера входных данных, равная максимальному количеству элементарных операций, проделываемых алгоритмом для решения экземпляра задачи указанного размера. «Существует связь между объемом входных данных (n) и количеством выполненных операций (N) относительно времени».
Константное (постоянное) время — O(1)
Линейное время — O(n)
Логарифмическое время — O(log(n))
Квадратичное время — O(n²)
Кубическое время — O(n³)
Как правило, мы стремимся создать алгоритм, который будет выполняться за константное время: O(1). Это значило бы, что время выполнения алгоритма одинаково независимо от размера набора данных или количества входных данных. Логарифмическая временная сложность — O(log (n)) — указывает на то, что по мере роста размера входных данных количество операций растет логарифмически (или достаточно медленно). С другой стороны, алгоритм, который может похвастаться кубической временной сложностью — O (n³) — имеет время выполнения, пропорциональное кубу размера набора данных. В результате добросовестный программист попытается свести к минимуму временную сложность своих алгоритмов и методов, чтобы уменьшить время выполнения и затрачиваемые ресурсы.
На приведенном ниже графике показано сравнение различных временных сложностей:

Длина кода
Не следует путать временную сложность с количеством строк кода. Такой показатель, как количество строк кода чрезвычайно легко измерить, но почти невозможно интерпретировать. В первую очередь это потому, что один алгоритм может иметь меньшую временную сложность при количестве строк кода большем, чем у другого алгоритма со сравнительно большей временной сложностью. Ошибочно считать, что временная сложность напрямую связана с количеством строк кода.
Давайте рассмотрим это на примере конкретной задачи: даны массив целых чисел nums и целое число target, нам нужно вернуть индексы двух чисел, которые в сумме равны target. Алгоритмы, решающие эту задачу, могут иметь разные временные сложности.
Реализация с временной сложностью O(n²):
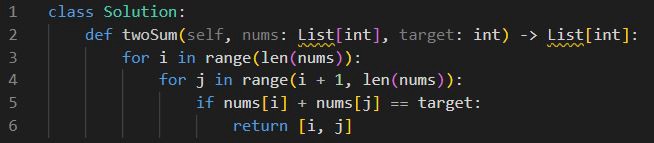
Реализация с временной сложностью O(n):

Оба этих подхода возвращают один и тот же результат. Однако мы прекрасно видим, что, несмотря на наличие дополнительной строки кода, второй пример выполняет задачу с временной сложностью O(n), а не O(n²), что в подавляющем большинстве случаев намного быстрее.
Несмотря на это, алгоритмы с меньшим количеством строк кода зачастую менее сложны, более читабельны и проще в использовании. Далее мы будем рассматривать разные алгоритмические подходы к одной и той же задаче, поэтому вполне ожидаемо, что все алгоритмы поиска решения лабиринта будут приблизительно одинакового объема. Следовательно, длину кода алгоритма все таки следует рассматривать как критерий при сравнении и противопоставлении рассматриваемых нами алгоритмов.
Алгоритмы поиска решения лабиринта
Алгоритмы поиска решения лабиринта представляют собой автоматизированные методы прохода. Отталкиваясь от конкретного лабиринт, можно использовать множество различных алгоритмов для нахождения его решения. В этой статье мы обсудим и проанализируем следующие хорошо известные алгоритмы поиска решения лабиринта:
Полный перебор/”Грубая сила” (Bruteforce Algorithm)
Алгоритм Тремо (Trémaux Algorithm)
Алгоритм случайного поведения мыши (Random Mouse Algorithm)
Метод следования вдоль стены (Wall-Follower Method)
Метод обнаружения тупиков (Dead-End Filling)
Алгоритм полного перебора
Алгоритм поиска решения лабиринта путем полного перебора (в простонародье “брутфорс”) исследует каждый проход, пока не найдет правильный путь. Работа алгоритмов такого типа обычно заключается в проверке всех возможных путей через лабиринт с постоянным перезапуском, когда сгенерированный путь оказывается неудачным. Такой подход зачастую имеет высокую временную сложность и делает программу неэффективной, поскольку она выполняет избыточный код. В результате временная сложность алгоритма такого типа часто составляет O(n!). С другой стороны, алгоритм полного перебора очень легок в реализации, поскольку он не требует маркировки развилок (что требуется для алгоритма Тремо) и зачастую состоит из небольшого количества операторов повторяющихся в цикле.
Алгоритм Тремо
Алгоритм Тремо, изобретенный Шарлем Пьером Тремо (Charles Pierre Trémaux), представляет из себя метод поиска решения лабиринта, который, чтобы обозначить путь, рисует линии и точки на протяжении всего лабиринта. Существует ряд правил, которым необходимо следовать в рамках этого алгоритма:
Выберите случайный проход и следуйте по нему до следующей развилки.
Помечайте начало и конец каждого прохода по мере их прохождения (на анимации ниже в качестве меток используются точки).
Если вы идете по проходу в первый раз, то вам нужно помечать его одной точкой.
Если вы зашли в тупик, вернитесь назад по тому же пути до первой развилки, пометив этот проход вторыми точками (на анимации две точки представлены крестом).
Проход, который отмечен двумя точками (на анимации это крест), не подлежит проходу и считается тупиком.
На развилке всегда выбирайте проход, отмеченный наименьшим количеством точек (в идеале не отмеченный ни одной точкой).
Этот алгоритм накладывает дополнительное требование помечать каждую пройденную развилку. Однако этот алгоритм более эффективен и имеет меньшую временную сложность, чем алгоритмы полного перебора и случайной мыши. Цена этой эффективности - более высокая сложность реализации. Впоследствии этот алгоритм был обобщен и назван “поиск в глубину”.
*Демонстрация работы алгоритма Тремо:

Пример реализации алгоритма Тремо на Python:
import random
from walker_base import WalkerBase
FOUND_COLOR = 'red'
VISITED_COLOR = 'gray70'
class Tremaux(WalkerBase):
class Node(object):
__slots__ = 'passages'
def __init__(self):
self.passages = set()
def __init__(self, maze):
super(Tremaux, self).__init__(maze, maze.start(), self.Node())
self._maze.clean()
self._last = None # Заготовка на будущее
def _is_junction(self, cell):
return cell.count_halls() > 2
def _is_visited(self, cell):
return len(self.read_map(cell).passages) > 0
def _backtracking(self, cell, last):
return last in self.read_map(cell).passages
def step(self):
# Сердечно прошу простить меня за этот ход
if self._cell is self._maze.finish():
self._isDone = True
self.paint(self._cell, FOUND_COLOR)
return
# print self._cell.get_position()
paths = self._cell.get_paths(last=self._last)
# print paths
random.shuffle(paths)
if self._is_visited(self._cell):
# Мы уже были здесь раньше
if self._backtracking(self._cell, self._last):
# Возвращаемся назад; проверяем, если какие-нибудь непосещенные отрезки пути
unvisited = filter(lambda c: not self._is_visited(c), paths)
if len(unvisited) > 0:
self._last = self._cell
self._cell = unvisited.pop()
else:
# Непосещенных отрезков пути нет
self.paint(self._cell, VISITED_COLOR)
# Ищем путь назад
passages = self.read_map(self._cell).passages
unvisited = set(self._cell.get_paths()).difference(passages)
self._last = self._cell
self._cell = unvisited.pop()
else:
# Мы пришли к уже посещенному ранее отрезку; разворачиваемся назад
self._cell, self._last = self._last, self._cell
else:
# Новый отрезок; двигаемся в случайном порядке
if len(paths) > 0:
# Не тупик
self.paint(self._cell, FOUND_COLOR)
self._last = self._cell
self._cell = paths.pop()
else:
# Тупик; возвращаемся
self.paint(self._cell, VISITED_COLOR)
self._cell, self._last = self._last, self._cell
self.read_map(self._last).passages.add(self._cell)
# print self.read_map(self._cell).passages
# print self.read_map(self._last).passages
# raw_input('...')Алгоритм случайного поведения мыши
Алгоритм случайного поведения мыши — крайне неинтеллектуальный и простой алгоритм. Часто он реализуется в качестве самого быстрого и простого варианта. В рамках этого алгоритма, как только мы начинаем двигаться по лабиринту и достигает развилки, мы “как мышь в лабиринте” случайным образом выбираем направление, в котором продолжим путь:
Следуем по текущему проходу, пока на пути нам не встретится развилка.
Затем мы случайным образом принимаем решение о следующем направлении, по которому мы будем следовать.
Этот алгоритм практически вслепую ищет выход из лабиринта и обычно занимает очень много времени. Несмотря на все это, мы всегда получим решение, так как алгоритм (“мышь”) в конечном итоге обязательно найдет правильный путь через лабиринт. Случайность и неэффективность, связанные с алгоритмами случайного поведения мыши, почти всегда являются причиной высокой временной сложности. Однако, этот алгоритм может случайным образом найти правильный путь с первой попытки/цикла, что дает нам временную сложность в лучшем случае O(1). Но, скорее всего, этот алгоритм будет неоднократно перебирать неудачные варианты, которые мы уже опробовали.
Пример кода алгоритма случайного поведения мыши на Python:
from random import choice
from maze_constants import *
from walker_base import WalkerBase
MOUSE_COLOR = 'brown'
class RandomMouse(WalkerBase):
def __init__(self, maze):
super(RandomMouse, self).__init__(maze, maze.start())
self._maze.clean()
self._last = None
self._delay = 50
def step(self):
if self._cell is self._maze.finish():
self._isDone = True
return
paths = self._cell.get_paths(last=self._last)
if len(paths) == 0:
# Мы попали в тупик
self._cell, self._last = self._last, self._cell
else:
self._last = self._cell
self._cell = choice(paths)
self.paint(self._cell, MOUSE_COLOR)
self.paint(self._last, OPEN_FILL)Метод следования вдоль стены
Одним из наиболее широко известных методов поиска решения лабиринтов является метод следования вдоль стены, также известный как “правило левой/правой руки”. Этот метод основан на внешней связности лабиринта — все стены должны быть соединены с внешней границей лабиринта. Если это так, то всегда можно найти выход из лабиринта, непрерывно следуя либо по левой, либо по правой стороне на протяжении всего лабиринта. Однако в тех случаях, когда не все стены соединены с внешними границами, этот метод не всегда будет находить решение. Этот метод/алгоритм полезен, если нам известно, что стены лабиринта связаны между собой. Алгоритм очень эффективен, так как не требует маркировки развилок или перезапуска при неудачных попытках; алгоритм просто следует по левой или правой стороне лабиринта.
Программирование метода следования вдоль стеной, вероятно, будет относительно простым и не потребует большого количества строк кода. В результате временная сложность, несомненно, будет лучше, чем у алгоритма полного перебора или случайного поведения мыши. Тем не менее, явная бесполезность этого метода для множество лабиринтов является большим минусом.
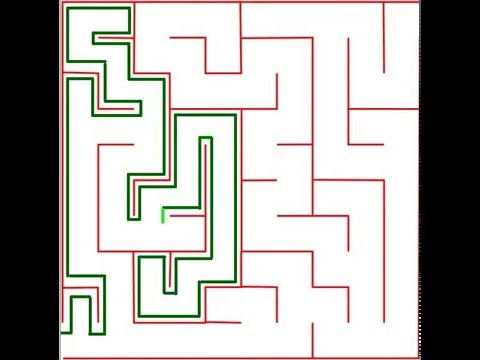
Пример реализации алгоритма следования вдоль стены.
Метод обнаружения тупиков
Алгоритм обнаружения тупиков использует другой подход к поиску решения лабиринта. Вместо того, чтобы пытаться пройти лабиринт как можно быстрее и эффективнее, алгоритм обнаружения тупиков заполняют все тупики, оставляя только правильный(е) путь(и). Правила этого алгоритма:
Найти все тупики в лабиринте.
Заполнить каждый путь из каждого тупика.
Последний (оставшийся) путь является правильным путем.
Преимущества использования алгоритма обнаружения тупиков заключаются в том, что он может найти несколько решений лабиринта, если они существуют, и алгоритм должен работать для любого типа лабиринта. Несмотря на это, алгоритм очень неэффективен, особенно если лабиринт большой. Алгоритм должен проверять каждый тупик, а затем заполнять/отмечать его. Это отнимает много времени и наводит меня на мысль, что любая более-менее разумная программа с реализацией этого алгоритма будет иметь временную сложность не менее O(n²). Видео алгоритма в действии можно посмотреть ниже:
Пример приложения с роботом
Я решила внедрить вышеперечисленные алгоритмы поиска решения лабиринта в настоящего робота, который будет пытаться найти выход из реального лабиринта. Сделать это можно с помощью Raspberri Pi Pico и MicroPython.
В этом проекте используется робот Yahboom Raspberry Pi Pico Robot:

В рамках этого руководства вам не помешало бы некоторое знание Python. Робот Yahboom Pico поставляется с Raspberry Pi Pico, и вы также можете докупить множество дополнительных в рамках набора Pico Sensor Kit. В этом проекте не будут использоваться датчики из набора Sensor Kit, поэтому вам достаточно приобрести только Pico Robot.
Для начала нам нужно будет собрать робота Yahboom из отдельных частей и Raspberry Pi Pico, а затем подготовить для запуска MicroPython. Колеса должны быть тщательно выровнены, чтобы избежать ошибок в движений при выполнении кода. MicroPython — это язык программирования, написанный на C и оптимизированный для работы на микроконтроллерах и аппаратных средствах. Он позволяет нам управлять оборудованием, подключенным к Raspberry Pi Pico, не сталкиваясь с трудностями, связанными с языками более низкого уровня, такими как C или C++.
После того, как все будет подготовлено, мы сможем протестировать различные алгоритмы на реальном лабиринте, собранном из цветных листов бумаги и пенопласта.
Установка программного обеспечения
Raspberry Pi Pico можно запрограммировать, подключив его к компьютеру через кабель micro-USB. Но для начала нам нужно установить MicroPython, после чего мы сможем начать программирование на устройстве. Самые актуальные версии файлов MicroPython UF2 можно найти в документации Raspberri Pi по MicroPython.

*Обратите внимание, что на Pico нужно удерживать BOOTSEL, чтобы библиотека отобразилась в Windows/Mac.
Кроме того, должны быть установлены компиляторы Thonny Python и MicroPython. Thonny позволит нам общаться с Raspberry Pi Pico и устройствами, подключенными к его контактам. Если MicroPython установлен на Raspberry Pi Pico, то соответствующая опция должна быть доступна в настройках интерпретатора Thonny:
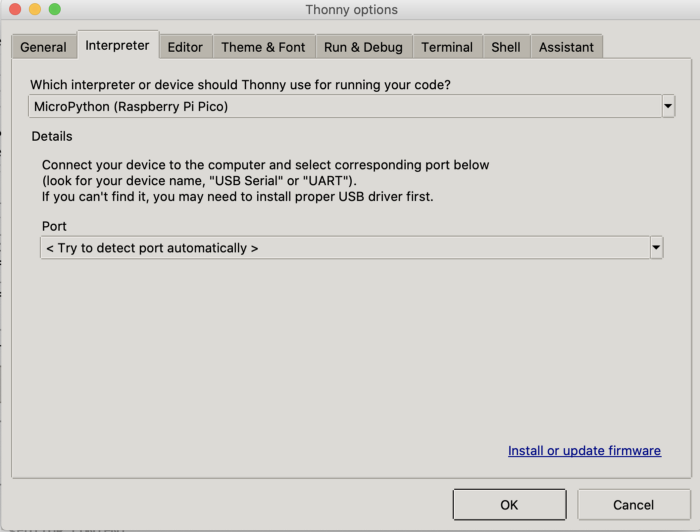
После успешного подключения к Thonny мы сможем получить доступ к Raspberry Pi Pico и начать программирование. Python-библиотека, которую рекомендуют производители робота, называется “Pico_Car”. Ее можно скачать здесь в разделе “библиотека” и впоследствии установить на Raspberry Pi Pico через Thonny. Кроме того, производители предоставляют приложение YahboomRobot на iOS для управления роботом. Чтобы использовать приложение, на Raspberry Pi Pico нужно загрузить и запустить “Bluetooth Control.py”. Файл можно скачать здесь в каталоге: “3. Robotics Course”. Если все правильно установлено и успешно запущено, то приложение должно выглядеть как на рисунке ниже, предоставляя нам возможность управлять роботом в режиме реального времени:

Чтобы управлять Raspberry Pi Pico без необходимости использовать это IOS-приложение, которое не позволяет нам запускать свой код, нам нужно реализовать управление через Bluetooth самостоятельно. Для этого мы должны использовать приложение для Android - Serial Bluetooth Terminal. Это приложение позволяет нам подключиться к Bluetooth-модулю Raspberry Pi Pico. Как только Pico получает ввод, определенный код может быть запущен или остановлен. Это позволяет нам запускать и останавливать программы по беспроводной связи и без необходимости подключать Pico к компьютеру каждый раз, когда нам нужно запустить фрагмент кода.
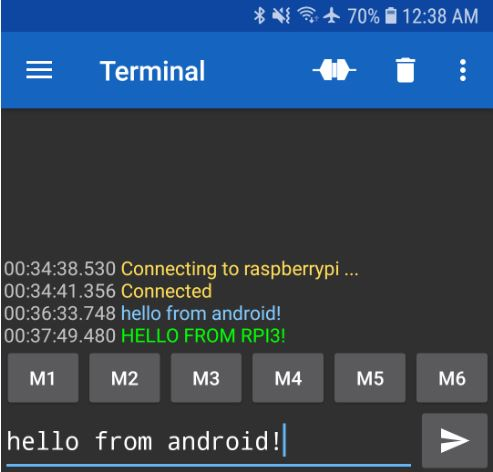
Значения M1 и M2 должны быть установлены в шестнадцатеричном формате в 31 и 32, чтобы запустить и остановить лабиринт соответственно.
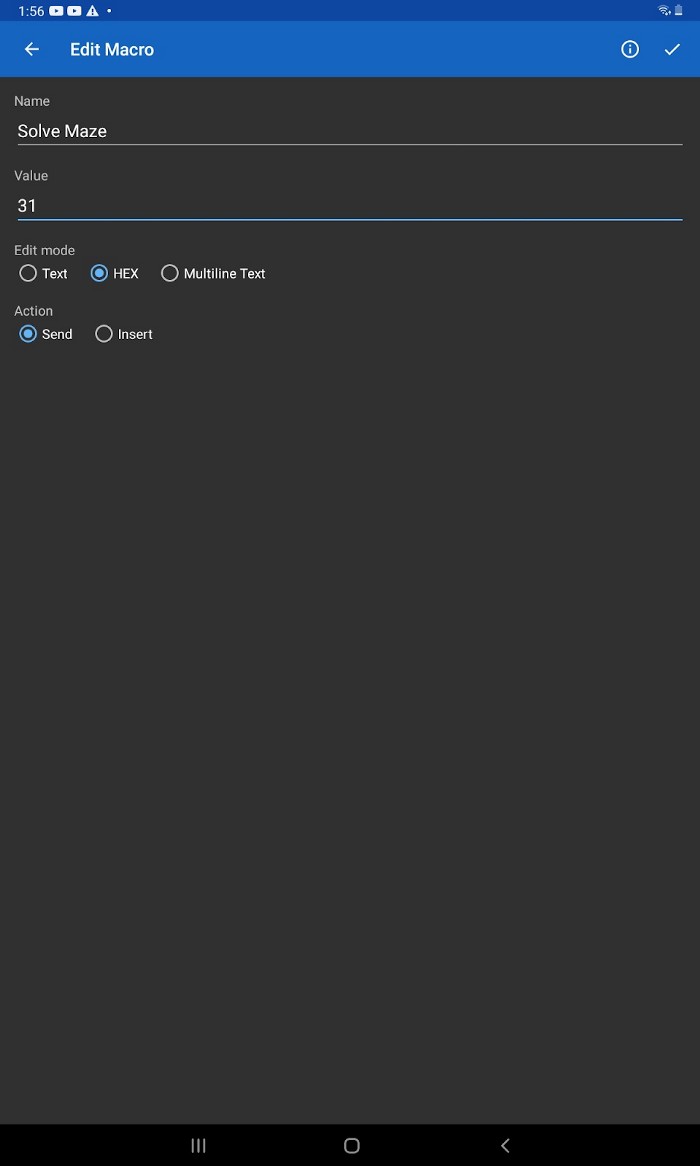
Теперь наконец настало время реализовать на практике алгоритмы, которые мы обсуждали в первой части этой статьи. Для начала нам нужно написать код полного перебора, адаптированный к аппаратному обеспечению Raspberry Pi Pico. В этом случае нам не нужно беспокоиться об использовании датчика цвета, поскольку мы просто используем уже инициализированный 2D-массив в качестве нашего лабиринта. Используя шаги, которые программа возвращает для решения лабиринта (например, влево, вправо, вверх или вниз), мы можем заставить робота двигаться в этих направлениях. Адаптированный код можно посмотреть здесь.


Используя реализованный алгоритм поиска решения лабиринта методом полного перебора (ссылка выше), робот может пройти предварительно указанный ей лабиринт. Если немного подкорректировать размеры лабиринта и ввести в код в виде двумерного массива под именем maze, то алгоритм может быть приспособлен для решения любого лабиринта. Стены/границы представлены в массиве как 1, а открытое пространство, через которое робот может пройти, представлено как 0:

Если бы это был реальный лабиринт, он выглядел бы следующим образом (начиная с левого верхнего индекса):

Поскольку Raspberry Pi Pico и его код теперь настроены, мы можем воссоздать лабиринт в реальной жизни, чтобы наш робот мог его пройти. Обратите внимание, что для bruteforcesolverRPIPICO.py, может потребоваться корректировка переменных speed и runtime в соответствии с масштабом и размерами лабиринта. Значение по умолчанию:
runtime = 2 #seconds
rotate_pause = 2 #seconds
speed = 175
Теперь робот может успешно пройти описанный выше лабиринт. Однако мы должны воссоздать лабиринт в реальной жизни. В этом случае для строительства стен лабиринта я буду использовать блоки пенопласта.

Пример робота, проходящего через лабиринт, можно найти в видео на YouTube:
В результате мы:
Собрали робота
Установили необходимое программное обеспечение (MicroPython и Thonny)
Убедились, что MicroPython установлен на Raspberry Pi
Настроили и запустили скрипт, не забыв взглянуть на уже готовое приложение под iOS.
Построили лабиринт и запустите скрипт с помощью Thonny, подключив робота к ПК
Реальные сценарии
Способность проходить лабиринты с помощью робота захватывает, но может быть трудно реализовать альтернативные применения этих алгоритмов в реальной жизни. Поиск решения лабиринта — это упрощенная версия задачи навигации, поэтому реализация алгоритмов навигации зиждется на тех же концепциях, что и поиск решения лабиринта.
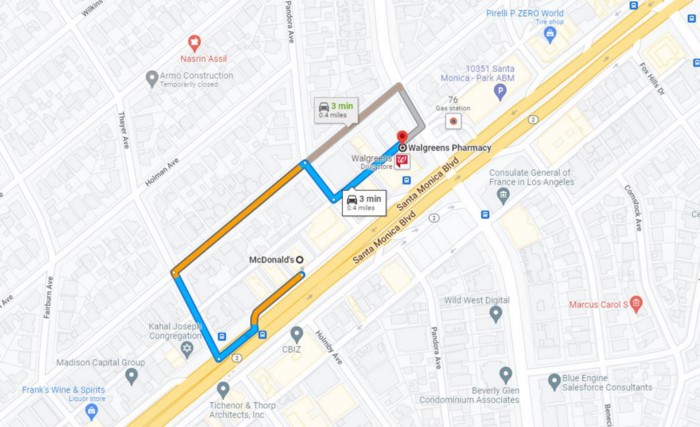
На примере ниже мы можем увидеть работу навигации Google Maps, где для построения пути от Mcdonald's до Walgreens Google тоже использует алгоритм для определения самого быстрого маршрута. Дороги в этом случае эквивалентны проходам в лабиринте (индексы со значениями 0 в массиве лабиринта). Google также пытается найти самый быстрый маршрут — обычно маршрут с наименьшим количеством поворотов и совокупным расстоянием.
Кроме того, в 2022 году Uber начал эксперименты с доставкой еды при помощи роботов; используя технологию поиска пути и GPS, холодильник на колесах будет доставлять покупателям их еду.

Дело в том, что аналогичные процессы и алгоритмы, используемые для нахождения решений лабиринтов, используются в интересных и очень полезных реальных приложениях. Не следует рассматривать концепцию поиска решения лабиринтов как изолированную область с немногими полезными применениями в реальной жизни, это не так.
Заключение
Роботы, способные находить путь в лабиринтах, — это концепция, которую многие могут счесть неинтересной или не столь ценной для общества. Однако для реализации этого проекта потребовалось всего около сотни строк кода. Кроме того, если бы алгоритм решения лабиринта полным перебором был адаптирован для использования датчика света или цвета, робот мог бы пройти любой лабиринт, не требуя предварительной информации о его размерах и конфигурации стен. Если бы у меня было больше времени, я бы обязательно реализовала эту идею в данном проекте. В ходе этого исследования я погрузилась в новую область удивительного мира алгоритмов, временной сложности и эффективности программ. Этот проект позволил мне в комфортном для меня темпе открыть для себя ранее неизведанную область исследований и ее связь с системами GPS и множеством перспективных идей и стартапов. В мире, которым вполне вероятно скоро будет править ИИ и сложные роботы, я чувствую себя немного спокойнее, зная, что получила важный опыт, экспериментируя с основами робототехники и алгоритмов.
Полезные ссылки:
“A Brief History of Mazes: National Building Museum.” National Building Museum |, 17 Mar. 2017, https://www.nbm.org/brief-history-mazes/.
“Simple Maze Solution (Brute Force, Depth First), Python.” Gist, https://gist.github.com/Chuwiey/1e34ed9e65d41b735d8c.
mikeburnfire. “Trémaux’s Algorithm.” YouTube, YouTube, 10 July 2020, https://www.youtube.com/watch?v=RjWSlz-aEr8.
Maze Solution #3 — Tremaux’s Algorithm: V19FA Intro to Computer Science (CIS-1100-VU01). https://vsc.instructure.com/courses/6476/modules/items/713459.
Anubabajide. “Anubabajide/Maze-Runner: Autonomous Maze Navigation Robot Using a Raspberry Pi.” GitHub, https://github.com/anubabajide/Maze-Runner.
Genetic Algorithm for Maze Solving Bot — GitHub Pages. https://shepai.github.io/downloads/GeneticAlgorithmVsBrute_by_Dexter_Shepherd.pdf.
“Trémaux’s Algorithm” Sample Maze Solved [1] — Researchgate. https://www.researchgate.net/figure/Tremauxs-algorithm-sample-maze-solved-1_fig8_315969093.
Cedars-Sinai Medical Center. “With Smiles and Beeps.” Robots Help Nurses Get the Job Done, Cedars-Sinai Medical Center, 26 Nov. 2021, https://www.cedars-sinai.org/newsroom/robots-help-nurses-get-the-job-donewith-smiles-and-beeps/.
“Raspberry Pi Documentation.” MicroPython, https://www.raspberrypi.com/documentation/microcontrollers/micropython.html.
McFarland, Matt. “Uber to Test Delivering Food with Robots.” CNN, Cable News Network, 13 May 2022, https://www.cnn.com/2022/05/13/cars/uber-robot-delivery-la
Jarednielsen. “Big O Factorial Time Complexity.” Jarednielsencom RSS, https://jarednielsen.com/big-o-factorial-time-complexity/.
Сегодня вечером состоится открытый вебинар на тему «Создание ассоциативного массива», на котором мы начнем реализовывать популярную структуру данных «ассоциативный массив» для хранения пар (ключ, значение). Рассмотрим несколько алгоритмов для решения этой задачи и сравним их эффективность:
1. Параллельные массивы;
2. Отсортированные массивы;
3. Двоичные деревья поиска.Регистрация для всех желающих доступна по ссылке.

