29.10.2022 21:26
apolozov 33 12000 Источник

Представьте, что у вас есть функция random(), которая генерируют случайным образом значения в промежутке [0;1]

Вычислите значение числа \pi

Это один из популярных вопросов на собеседовании в топовую IT компанию

В первую секунду может показаться, что ваш интервьюер слегка издевается над вам, но если вспомнить основы из теории вероятности, то все становится гораздо проще. Let's go!

База из теории вероятности

Классическое определение вероятности.

Вероятность, что событие A произойдет, равно отношению количеству благоприятных исходов mк количеству всех возможных исходов n

На языке математики это выглядит так: P(A) = \frac{m}{n}

Например у нас есть кубик. Какая вероятность что выпадет грань с четными значениями?

Решение

Набор всех исходов {{1, 2, 3, 4, 5, 6}} \Rightarrow n=6
Набор благоприятных исходов A= {2, 4, 6} \Rightarrow m=3
Значит P(A) = \frac{3}{6} = \frac{1}{2}

Геометрическое определение вероятности.

Предыдущее определение вероятности отличное, но оно обладает несколькими существенными ограничениями. Одним из таких ограничений является тот факт, что оно неприменимо к испытаниям с бесконечным количеством исходов. 

Чтобы стало понятно о чем речь - давайте решим задачку.

На отрезок [0;1]случайным образом брошена точка M.Найдите вероятность того, что она попадет в промежуток [0,5; 0,8]

Понятно, что здесь не получится использовать классическое определение, поскольку на отрезке бесконечно много точек. Тогда нам идет на помощь геометрическое определение

вероятности P(A)=\frac{S(A)}{S(\Omega)}, в нашем случае S(A) = 0.8 - 0.5=0.3, S(\Omega)=1

Следовательно P(A)=0,3

Решение задачи

Концепция

Построим геометрическую модель.

Введем систему координат с осями xи y
Расположим квадрат с единичной стороной, так чтобы начало системы координат находилось в левом углу.
Нарисуем единичный круг с центром в начале координат.

геометрическая модель
геометрическая модель

Будем случайным образом располагать точку в квадрате.
Наша исходная задача сводится к следующему вопросу.
Какая вероятность, что точка попадет в верхнюю правую четверть круга (область A)

Мы знаем, что S_{квадрата} = 1, а S_{A} =\frac{\pi r^2}{4}=(r=1)=\frac{\pi}{4}

Значит вероятность того, что точка попадет в искомую область равна P(A)=\frac{\pi}{4}

С другой стороны, после распределения n точек по квадрату, мы можем оценить количество точек, которое попало внутрь круга. Для этого точка с координатами (x,y)

должна удовлетворять неравенству \sqrt{x^2+y^2}\leq1

Тогда вероятность P(A)=\frac{m}{n}, где mколичество точек попавших внутрь круга, а n общее число точек.

Значит из верних соотношений имеем P(A)=\frac{\pi}{4}=\frac{m}{n} \Rightarrow \pi=4*\frac{m}{n}

Программируем

import random

def estimate_pi(n):
    num_point_circle = 0 #кол-во точек внутри круга
    num_point_total = n

    for i in range(n):
        x = random.uniform(0,1)
        y = random.uniform(0,1)
        distance = x**2 + y**2

        if distance <= 1: #определяем, что точка попала внутрь круга
            num_point_circle += 1

    return 4 * num_point_circle/num_point_total

n = 10000000 #общее количество точек (чем больше точек, тем лучше точность)
pi =  estimate_pi(n)

print(pi)

На этом все!

Надеюсь вам понравилась задача! Делитесь своими интересными задачками с собеседований, будем разбирать)

Связаться со мной @polozovs

Комментарии (33)


  1. middle
    29.10.2022 21:28
    #24863752
    +22

    Испокон веков для подсчёта числа пи использовали иголку.


    1. apolozov Автор
      29.10.2022 21:39
      #24863778

      Почитал, очень интересно и необычно)


  1. Markscheider
    29.10.2022 21:35
    #24863764
    +5

    Элегантно и просто. Спасибо.

    Единственное что -- вместо

    круг с центром в начале координат едичного радиуса

    привычнее читать "единичная окружность".


    1. apolozov Автор
      29.10.2022 21:38
      #24863774
      -1

      Да, так звучит лучше. Спасибо!


  1. cax
    29.10.2022 21:38
    #24863772
    +23

    Если мне не изменяет память, этот метод называется "метод Монте-Карло" ?


    1. middle
      29.10.2022 21:40
      #24863784
      +1

      Так и есть.


    1. apolozov Автор
      29.10.2022 21:42
      #24863786
      -1

      Википедия подсказывает, что это действительно так. Выше скидывали инфу как найти число пи с помощью иголки. Этот метод тоже из аналогичной группы численных методов для изучения случайных процессов.


    1. Source
      30.10.2022 00:48
      #24864098
      +11

      Я удивился, что в статье его не назвали. Это имхо и есть ответ на вопрос из собеседования: "Надо применить метод Монте-Карло", дальше всё довольно очевидно.

      Сомневаюсь, что кто-то не зная о нём, сможет прямо на собеседовании его придумать.


  1. panteleymonov
    30.10.2022 00:51
    #24864110
    +1

    Плохо соображаю на ночь глядя, но в целях оптимизации подумалось - если взять вместо круга сферу, то вероятность от трехмерной точки будет Пи/6. И таким образом увеличится вызов генератора случайного числа на одну итерацию до трех. Можно ли пойти в обратном направлении и уменьшить его до одного?


    1. thevlad
      30.10.2022 01:17
      #24864146
      +5

      Там надо не количество вызовов рандома оптимизировать, а сходимость у данного метода, которая достаточно паршивая и пропорциональна sqrt(n).

      PS: https://en.wikipedia.org/wiki/Quasi-Monte_Carlo_method


  1. Ninil
    30.10.2022 01:47
    #24864178
    +20

    Хмм... Уровень статей на Хабре непрерывно падает... мы этот метод разбирали в кружке информатики, когда я был в 6 классе. Метод Монте-Карло называется, причём первая же ссылка в поисковике(у меня по крайней мере) — на статю на хабре https://habr.com/ru/post/128454

    Ждём статей с программами вида «Звездное небо» и «вычисление факториала» %)))


    1. Source
      30.10.2022 03:48
      #24864278
      +4

      причём первая же ссылка в поисковике(у меня по крайней мере) — на статю на хабре

      которую справедливо заминусовали за бессодержательность и округления)

      Да, 11 лет назад Хабр был более требователен к качеству материала.


      1. ne555
        30.10.2022 09:48
        #24864518
        +1

        Да, 11 лет назад Хабр был более требователен к качеству материала.

        Такие высказывания встречаются нередко в комментах, типо: "статьи на Хабре раньше были лучше". Не соглашусь. Иногда в поисковике попадаются ссылки на статьи 10-летней давности и качество там "стыд 2010". Пример.


        1. Source
          30.10.2022 12:58
          #24864902

          Не соглашусь. Иногда ..

          Ключевое слово "иногда"


          1. ne555
            30.10.2022 13:20
            #24864930
            +1

            Да, иногда, но рандомно поманипулировал с url-Хабра рядом с 2010г., получаю низкосортные заметки, а не статьи технического уровня:


            1. Source
              30.10.2022 13:50
              #24864996

              А вы по какой логике их отбираете? Из 4 статей, только одна с рейтингом больше 20. И то в дисклеймере честно написано, что это комментарий выделенный в статью. Значит на тот момент на это был запрос, т.к. лицензии Creative Commons были не столь известны, как сейчас.

              Вы сравнивайте как сообщество реагирует на схожие статьи, а надёргать из поисковика то, что и в ленты то в своё время не попадало, всегда можно.

              P.S. А статьи из хабов "Блог компании X" вообще редко отличаются качеством, но они тут в качестве рекламы.


              1. ne555
                30.10.2022 14:28
                #24865076

                А вы по какой логике их отбираете?

                рандомно поманипулировал с url-Хабра рядом с 2010г.

                т.е. я даже не пытался выбрать что-то самое level уровня: 10 предложений.

                от момент на это был запрос, т.к. лицензии Creative Commons

                Там даже не постеснялись метку поставить "tutorial".

                "Блог компании X" вообще редко отличаются качеством, но они тут в качестве рекламы.

                Не хочу более спорить, но в некоторых корп.блогах пишут технически подкованные авторы, которые умеют и понимают (они также бы могли выдавать контент на высоком уровне и без рекламы, но их нашли и привлекли, контент не пострадал).

                А вывод я озвучил в своём первом комментарии в этой ветке. Ищите качественный контент, не стоит ограничиваться Хабром. Браузер с переводчиком, поиск по сайту и Nature; Science или Гугловская Академия. Там не так всё скверно с материалом прошлой эпохи. И пожалуй близкий к Хабру сайт — Slashdot.


    1. 0xd34df00d
      30.10.2022 19:12
      #24865614
      +2

      Ну про факториал есть что обсудить.


    1. andrejjm78
      01.11.2022 17:15
      #24872248

      А почему бы и нет. Лет 15 назад столкнулся с тем, что отсутствует толковое решение для комбинаторного расчета. Надо было найти число сочетаний из n объектов по k, причем точно. EXEL2003 вообще иногда выдавал дробные числа.

      С(7;1913)=18399302838933135756.


  1. longclaps
    30.10.2022 07:01
    #24864348
    +17

    У статьи два тэга: Python и Математика. Это прекрасно.

    Начнем с питона, перепишем авторское решение, сохранив его идею:

    from random import random

def estimate_pi(n):
    s = 0.
    for _ in range(n):
        x, y = random(), random()
        if 1. >= x * x + y * y:
            s += 4.
    return s / n

    Хм, в CPython 3.10 это работает в 3.5 раза быстрее. Как же так, дружище? Как же тэг Python?

    Ладно, что там с математикой? Про сходимость тут уже высказались, хорошо бы немного практики, чтобы цифры пощупать. Считаем по-всякому площадь сектора OAC.

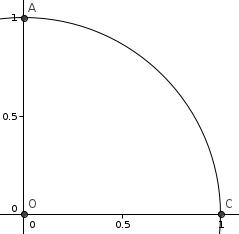
    Я умею интегрировать трапециями!

    from math import sqrt

def trapezoid_pi(n):
    s = .5  # значения в крайних точках интервала
    # берутся с весом 0.5, а значения эти - 1 и 0
    x = step = 1. / n
    for _ in range(n - 1):
        s += sqrt(1. - x * x)
        x += step
    return s * 4. / n

    Я могу интегрировать по Симпсону!

    from math import fsum

def simpson_pi(n):
    x, step, res = 0, 1. / n, [.5]
    for _ in range(n):
        x += step
        res.append(sqrt(1. - x * x))
    return (fsum(res[::2]) + fsum(res[1::2]) * 2.) * 8. / (n * 3)

    Правда, это даёт выигрыш в точности против трапеции всего 2.5 раза. Всё из-за особенности в точке C - там касательная к окружности идёт отвесно. Так это можно обойти: отдельно посчитаем площадь сегмента AB и четырехугольника OABC.

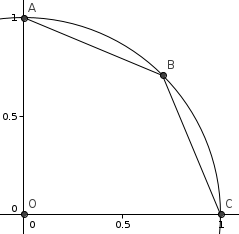
    from math import fsum, sqrt

def simpson45_pi(n):
    x, step, res, s5 = 0., 1. / n, [.0], sqrt(.5)
    for _ in range(n):
        x += step
        res.append(sqrt(1. - x * x * .5) - 1. + (1. - s5) * x)
    AB = (fsum(res[::2]) + fsum(res[1::2]) * 2.) * s5 * 2. / (n * 3)
    OABC = s5  # взял аналитически 
    return (OABC + AB * 2.) * 4.

    Да, а как же цифры? Вот они:

    Абсолютная погрешность против библиотечного значения π для n = 2 ** 3 == 8
(разбиение интервала на степень двойки дает мне выигрыш в точности)

estimate_pi   0.47564011559266456 # усредненно по большой выборке
trapezoid_pi  0.05177350923261992
simpson_pi    0.02040348381437518
simpson45_pi  0.00003003695260295


Погрешность для n = 2 ** 13, мельчить сильнее вроде незачем

estimate_pi   0.01486375361227077 # усредненно
trapezoid_pi  0.00000158604010281
simpson_pi    0.00000061939277884
simpson45_pi  0.00000000000000000

    Ну что тут скажешь? Друзья, не суйте Монте-Карло куда попало.

    А можно еще и с NumPy, но уж это как-нибудь в другой раз.


    1. panteleymonov
      30.10.2022 12:09
      #24864764
      +9

      А где генератор случайного числа? С таким же успехом можно арксинус от единицы на два умножить.


    1. demoth
      30.10.2022 14:09
      #24865034
      +1

      Ну раз питон-питон, то тогда так :)

      def estimate_pi(n: int) -> float:
   return sum(4
              for _ in range(n)
              if (x := random()) * x + (y := random()) * y < 1) / n


    1. 9982th
      01.11.2022 17:15
      #24872246

      Львиную долю ускорения в вашем варианте дает замена random.uniform на random.random, из вызова которого первый, собственно, и состоит, убирая лишний вызов функции. На втором месте замена возведения в степень на умножение, эффект от которой не столь впечатляющий, но хорошо заметный.
      Не могли бы вы пояснить смысл остальных оптимизаций, в частности, замены int на float и инкремента на 4 вместо 1 в счетчике?


  1. MUTbKA98
    30.10.2022 08:19
    #24864408
    +2

    Я вижу по коду, что на самом деле разрешается не только RNG, но и сложения, умножения, возведения в степень. Не проще ли тогда сразу взять и вычислить ряд, например, а на RNG забить? Так и быстрее, и точнее.


  1. Newm
    30.10.2022 08:37
    #24864422

    Кстати задача довольно интересная... Для проверки качества функции псевдослучайных чисел.

    Когда я запускал такую программку почти 40 лет назад на агате, точность оказалась так себе...


  1. ne555
    30.10.2022 09:29
    #24864482
    -6

    Например у нас есть кубик. Какая вероятность что выпадет грань с четными значениями? 1/2

    Набор всех исходов 6

    А вот и нет, решение неверное. В задаче называется "кубик", у кубика есть не только грани (6), но и рёбра (12) и их вершины (8). И какова же вероятность, что кубик выпадет не на чёт.числе/грани, а на вершине или ребре? явно не 1/2, более того кубик на практике реально иногда встает не на грань.

    На отрезок [0;1].

    на отрезке бесконечно много точек

    Тоже не верно, отрезок конечный и точек у него также конечное число, зависит от шага.


    1. SilverHorse
      01.11.2022 00:13
      #24869880
      +1

      И какова же вероятность, что кубик выпадет не на чёт.числе/грани, а на вершине или ребре?

      Ноль. С математическими абстракциями вы не знакомы, похоже...

      Тоже не верно, отрезок конечный

      ...как и с теорией множеств и определениями конечного множества и отрезка...


  1. Alexander_The_Great
    30.10.2022 10:50
    #24864624
    +3

    Зумеры изобрели метод стат. анализа (Монте-Карло)?


  1. chelaxe
    30.10.2022 13:22
    #24864936

    P=lambda n:sum([(1-(1/n/2+i/n)**2)**.5/n for i in range(0,n)])*4
P(1_000_000)


  1. Naf2000
    30.10.2022 20:51
    #24865806
    +3

    Метод Монте-Карло именно на примере числа пи описан в школьном учебнике информатике (Кушниренко и другие) издательство 1989 года. Этому детей учили


    1. Ninil
      31.10.2022 01:58
      #24866396
      +1

      Но не все дети, видать, учились)


    1. ilia_bonn
      01.11.2022 17:14
      #24872242

      У меня метод монте карло ни в школе не проходили (13 классов гимназии в Германии), ни в институте по статистике при обучении на бакалавра по психологии (статистика была как предмет из блока методологии в первых двух семестрах по 4 академических часа в неделю в каждом).


  1. Batyr1992
    01.11.2022 17:15
    #24872244

    Статья довольно баянистая, хотя мне данная иллюстрация нравится) мне кажется стоило добавить оценку погрешности , обычно такое рассматривается в численных методах