1. Преобразование Фурье и спектр сигнала

Во многих случаях задача получения (вычисления) спектра сигнала выглядит следующим образом. Имеется АЦП, который с частотой дискретизации Fd преобразует непрерывный сигнал, поступающий на его вход в течение времени Т, в цифровые отсчеты — N штук. Далее массив отсчетов подается в некую программку, которая выдает N/2 каких-то числовых значений (программист, который утянул из инета написал программку, уверяет, что она делает преобразование Фурье).

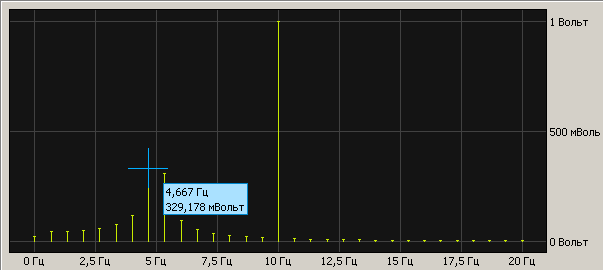
Чтобы проверить, правильно ли работает программа, сформируем массив отсчетов как сумму двух синусоид sin(10*2*pi*x)+0,5*sin(5*2*pi*x) и подсунем программке. Программа нарисовала следующее:


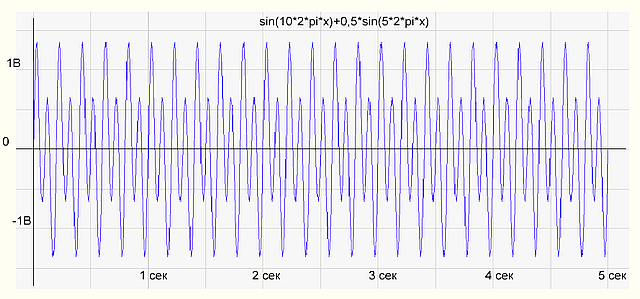
рис.1 График временной функции сигнала


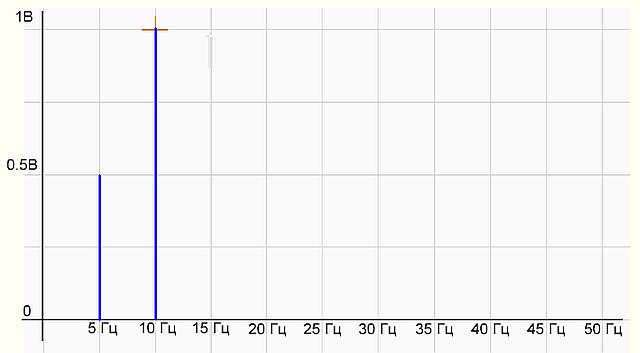
рис.2 График спектра сигнала

На графике спектра имеется две палки (гармоники) 5 Гц с амплитудой 0.5 В и 10 Гц — с амплитудой 1 В, все как в формуле исходного сигнала. Все отлично, программист молодец! Программа работает правильно.

Это значит, что если мы подадим на вход АЦП реальный сигнал из смеси двух синусоид, то мы получим аналогичный спектр, состоящий из двух гармоник.

Итого, наш реальный измеренный сигнал, длительностью 5 сек, оцифрованный АЦП, то есть представленный дискретными отсчетами, имеет дискретный непериодический спектр.

С математической точки зрения — сколько ошибок в этой фразе?

Теперь начальство решило мы решили, что 5 секунд — это слишком долго, давай измерять сигнал за 0.5 сек.


рис.3 График функции sin(10*2*pi*x)+0,5*sin(5*2*pi*x) на периоде измерения 0.5 сек


рис.4 Спектр функции

Что-то как бы не то! Гармоника 10 Гц рисуется нормально, а вместо палки на 5 Гц появилось несколько каких-то непонятных гармоник. Смотрим в интернетах, что да как…

Во, говорят, что в конец выборки надо добавить нули и спектр будет рисоваться нормальный.


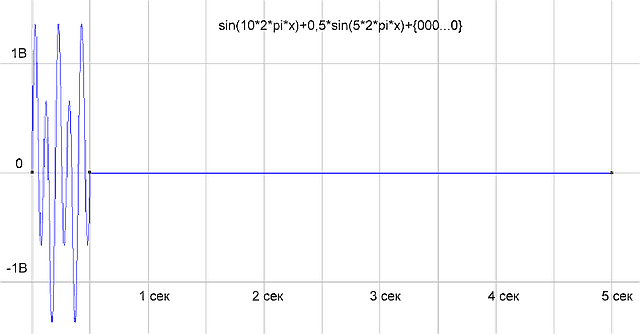
рис.5 Добили нулей до 5 сек


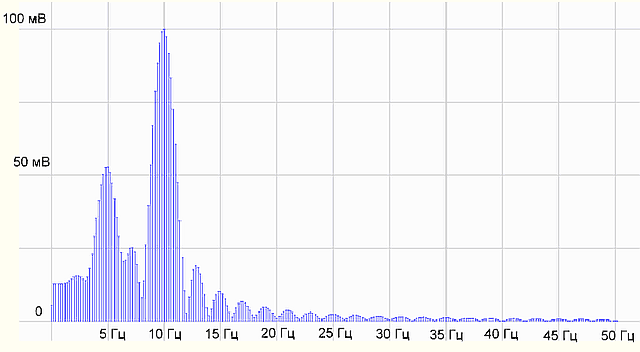
рис.6 Получили спектр

Все равно не то, что было на 5 секундах. Придется разбираться с теорией. Идем в Википедию — источник знаний.

2. Непрерывная функция и представление её рядом Фурье

Математически наш сигнал длительностью T секунд является некоторой функцией f(x), заданной на отрезке {0, T} (X в данном случае — время). Такую функцию всегда можно представить в виде суммы гармонических функций (синусоид или косинусоид) вида:

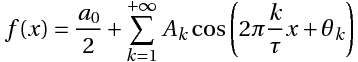(1), где:

k — номер тригонометрической функции ( номер гармонической составляющей, номер гармоники)
T — отрезок, где функция определена (длительность сигнала)
Ak — амплитуда k-ой гармонической составляющей,
?k- начальная фаза k-ой гармонической составляющей

Что значит «представить функцию в виде суммы ряда»? Это значит, что, сложив в каждой точке значения гармонических составляющих ряда Фурье, мы получим значение нашей функции в этой точке.

(Более строго, среднеквадратичное отклонение ряда от функции f(x) будет стремиться к нулю, но несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. См. https://ru.wikipedia.org/wiki/Ряд_Фурье.)

Этот ряд может быть также записан в виде:

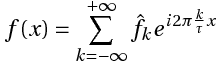(2),
где 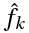, k-я комплексная амплитуда.

или

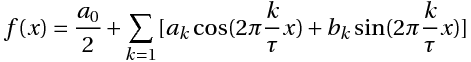(3)

Связь между коэффициентами (1) и (3) выражается следующими формулами:



и



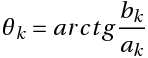
Отметим, что все эти три представления ряда Фурье совершенно равнозначны. Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. Но нам удобно использовать формулу (1), где ряд Фурье представлен в виде суммы косинусоид с соответствующими амплитудами и фазами. В любом случае неправильно говорить, что результатом преобразования Фурье действительного сигнала будут комплексные амплитуды гармоник. Как правильно говорится в Вики «Преобразование Фурье (?) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»

Итого:
Математической основой спектрального анализа сигналов является преобразование Фурье.

Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда) тригонометрических функций (синусоид и\или косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.

Отметим еще некоторые моменты, понимание которых требуется для правильного применения преобразования Фурье к анализу сигналов. Если рассмотреть ряд Фурье (сумму синусоид) на всей оси Х, то можно увидеть, что вне отрезка {0, T} функция представленная рядом Фурье будет будет периодически повторять нашу функцию.

Например, на графике рис.7 исходная функция определена на отрезке {-T\2, +T\2}, а ряд Фурье представляет периодическую функцию, определенную на всей оси х.

Это происходит потому, что синусоиды сами являются периодическими функциями, соответственно и их сумма будет периодической функцией.


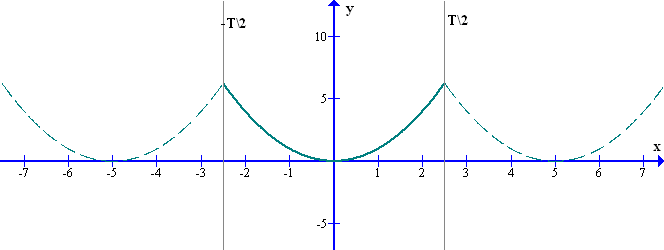
рис.7 Представление непериодической исходной функции рядом Фурье

Таким образом:

Наша исходная функция — непрерывная, непериодическая, определена на некотором отрезке длиной T.
Спектр этой функции — дискретный, то есть представлен в виде бесконечного ряда гармонических составляющих — ряда Фурье.
По факту, рядом Фурье определяется некоторая периодическая функция, совпадающая с нашей на отрезке {0, T}, но для нас эта периодичность не существенна.

Далее.

Периоды гармонических составляющих кратны величине отрезка {0, T}, на котором определена исходная функция f(x). Другими словами, периоды гармоник кратны длительности измерения сигнала. Например, период первой гармоники ряда Фурье равен интервалу Т, на котором определена функция f(x). Период второй гармоники ряда Фурье равен интервалу Т/2. И так далее (см. рис. 8).


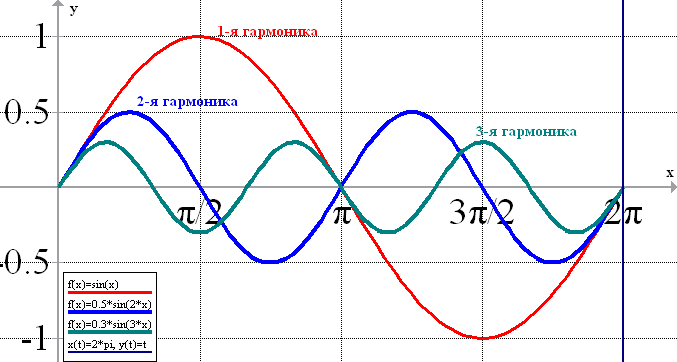
рис.8 Периоды (частоты) гармонических составляющих ряда Фурье (здесь Т=2?)

Соответственно, частоты гармонических составляющих кратны величине 1/Т. То есть частоты гармонических составляющих Fk равны Fk= к\Т, где к пробегает значения от 0 до ?, например к=0 F0=0; к=1 F1=1\T; к=2 F2=2\T; к=3 F3=3\T;… Fk= к\Т (при нулевой частоте — постоянная составляющая).

Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее.

Шаг между гармониками в этом случае равен 1 Гц.

Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.
Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.

Существует способ искусственного увеличения длительности сигнала путем добавления нулей к массиву отсчетов. Но реальную разрешающую способность по частоте он не увеличивает.

3. Дискретные сигналы и дискретное преобразование Фурье

С развитием цифровой техники изменились и способы хранения данных измерений (сигналов). Если раньше сигнал мог записываться на магнитофон и храниться на ленте в аналоговом виде, то сейчас сигналы оцифровываются и хранятся в файлах в памяти компьютера в виде набора чисел (отсчетов).

Обычная схема измерения и оцифровки сигнала выглядит следующим образом.


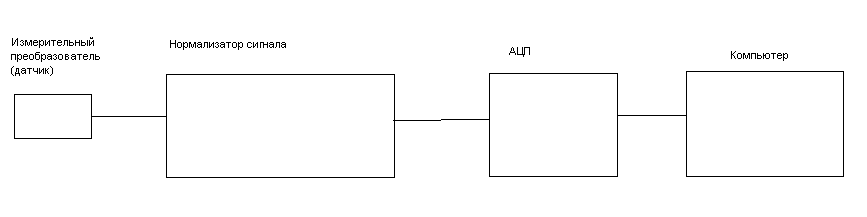
рис.9 Схема измерительного канала

Сигнал с измерительного преобразователя поступает на АЦП в течение периода времени Т. Полученные за время Т отсчеты сигнала (выборка) передаются в компьютер и сохраняются в памяти.


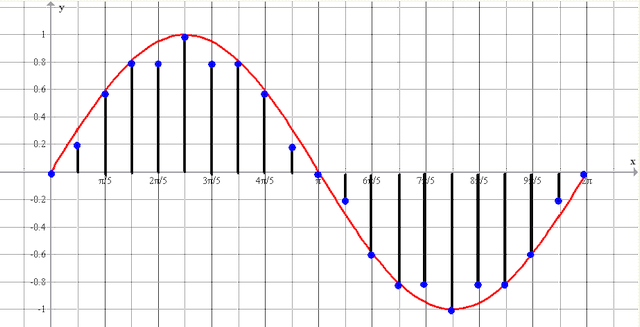
рис.10 Оцифрованный сигнал — N отсчетов полученных за время Т

Какие требования выдвигаются к параметрам оцифровки сигнала? Устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал) называется аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) ( Wiki).

Одним из основных параметров АЦП является максимальная частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в герцах. (( Wiki))

Согласно теореме Котельникова, если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени 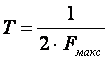, т.е. с частотой Fd ? 2*Fмакс, где Fd — частота дискретизации; Fмакс — максимальная частота спектра сигнала. Другими слова частота оцифровки сигнала (частота дискретизации АЦП) должна как минимум в 2 раза превышать максимальную частоту сигнала, который мы хотим измерить.

А что будет, если мы будем брать отсчеты с меньшей частотой, чем требуется по теореме Котельникова?

В этом случае возникает эффект «алиасинга» (он же стробоскопический эффект, муаровый эффект), при котором сигнал высокой частоты после оцифровки превращается в сигнал низкой частоты, которого на самом деле не существует. На рис. 5 красная синусоида высокой частоты — это реальный сигнал. Синяя синусоида более низкой частоты — фиктивный сигнал, возникающий вследствие того, за время взятия отсчета успевает пройти больше, чем пол-периода высокочастотного сигнала.


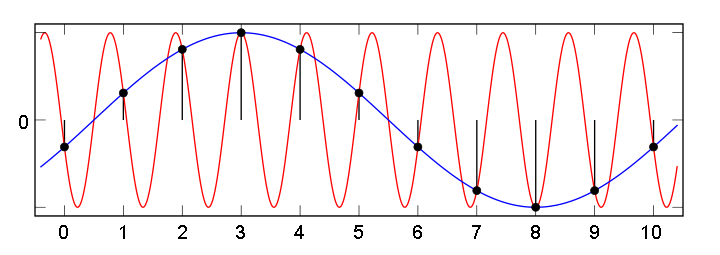
Рис. 11. Появление ложного сигнала низкой частоты при недостаточно высокой частоте дискретизации

Чтобы избежать эффекта алиасинга перед АЦП ставят специальный антиалиасинговый фильтр — ФНЧ (фильтр нижних частот), который пропускает частоты ниже половины частоты дискретизации АЦП, а более высокие частоты зарезает.

Для того, чтобы вычислить спектр сигнала по его дискретным отсчетам используется дискретное преобразование Фурье (ДПФ). Отметим еще раз, что спектр дискретного сигнала «по определению» ограничен частотой Fмакс, меньшей половине частоты дискретизации Fd. Поэтому спектр дискретного сигнала может быть представлен суммой конечного числа гармоник, в отличие от бесконечной суммы для ряда Фурье непрерывного сигнала, спектр которого может быть неограничен. Согласно теореме Котельникова максимальная частота гармоники должна быть такой, чтобы на нее приходилось как минимум два отсчета, поэтому число гармоник равно половине числа отсчетов дискретного сигнала. То есть если в выборке имется N отсчетов, то число гармоник в спектре будет равно N/2.

Рассмотрим теперь дискретное преобразование Фурье (ДПФ).



Сравнивая с рядом Фурье



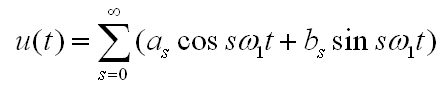
видим, что они совпадают, за исключением того, что время в ДПФ имеет дискретный характер и число гармоник ограничено величиной N/2 — половиной числа отсчетов.

Формулы ДПФ записываются в безразмерных целых переменных k, s, где k – номера отсчетов сигнала, s – номера спектральных составляющих.
Величина s показывает количество полных колебаний гармоники на периоде Т (длительности измерения сигнала). Дискретное преобразование Фурье используется для нахождения амплитуд и фаз гармоник численным методом, т.е. «на компьютере»

Возвращаясь к результатам, полученным в начале. Как уже было сказано выше, при разложении в ряд Фурье непериодической функции (нашего сигнала), полученный ряд Фурье фактически соответствует периодической функции с периодом Т. (рис.12).


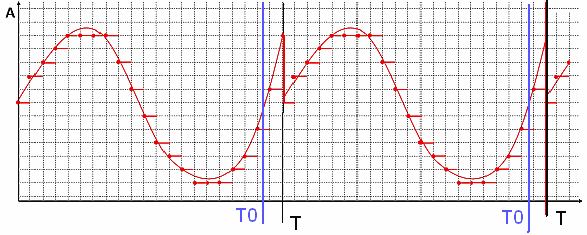
рис.12 Периодическая функция f(x) с периодом Т0, с периодом измерения Т>T0

Как видно на рис.12 функция f(x) периодическая с периодом Т0. Однако из-за того, что длительность измерительной выборки Т не совпадает с периодом функции Т0, функция, получаемая как ряд Фурье, имеет разрыв в точке Т. В результате спектр данной функции будет содержать большое количество высокочастотных гармоник. Если бы длительность измерительной выборки Т совпадала с периодом функции Т0, то в полученном после преобразования Фурье спектре присутствовала бы только первая гармоника (синусоида с периодом равным длительности выборки), поскольку функция f(x) представляет собой синусоиду.

Другими словами, программа ДПФ «не знает», что наш сигнал представляет собой «кусок синусоиды», а пытается представить в виде ряда периодическую функцию, которая имеет разрыв из-за нестыковки отдельных кусков синусоиды.

В результате в спектре появляются гармоники, которые должны в сумме изобразить форму функции, включая этот разрыв.

Таким образом, чтобы получить «правильный» спектр сигнала, являющегося суммой нескольких синусоид с разными периодами, необходимо чтобы на периоде измерения сигнала укладывалось целое число периодов каждой синусоиды. На практике это условие можно выполнить при достаточно большой длительности измерения сигнала.


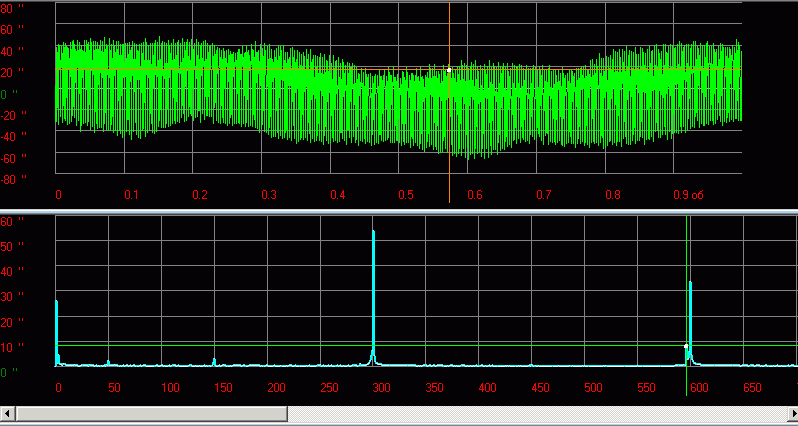
Рис.13 Пример функции и спектра сигнала кинематической погрешности редуктора

При меньшей длительности картина будет выглядеть «хуже»:


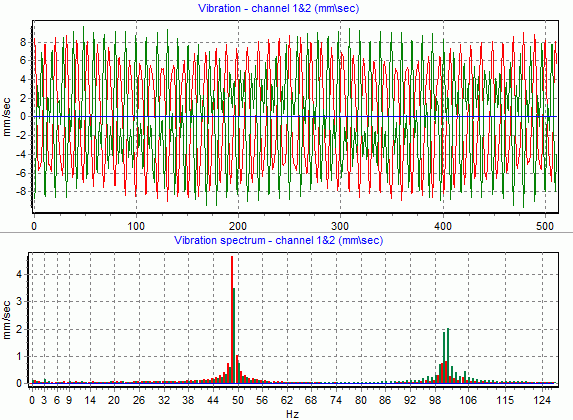
Рис.14 Пример функции и спектра сигнала вибрации ротора

На практике бывает сложно понять, где «реальные составляющие», а где «артефакты», вызванные некратностью периодов составляющих и длительности выборки сигнала или «скачками и разрывами» формы сигнала. Конечно слова «реальные составляющие» и «артефакты» не зря взяты в кавычки. Наличие на графике спектра множества гармоник не означает, что наш сигнал в реальности из них «состоит». Это все равно что считать, будто число 7 «состоит» из чисел 3 и 4. Число 7 можно представить в виде суммы чисел 3 и 4 — это правильно.

Так и наш сигнал… а вернее даже не «наш сигнал», а периодическую функцию, составленную путем повторения нашего сигнала (выборки) можно представить в виде суммы гармоник (синусоид) с определенными амплитудами и фазами. Но во многих важных для практики случаях (см. рисунки выше) действительно можно связать полученные в спектре гармоники и с реальными процессами, имеющими циклический характер и вносящими значительный вклад в форму сигнала.

Некоторые итоги

1. Реальный измеренный сигнал, длительностью T сек, оцифрованный АЦП, то есть представленный набором дискретных отсчетов (N штук), имеет дискретный непериодический спектр, представленный набором гармоник (N/2 штук).

2. Сигнал представлен набором действительных значений и его спектр представлен набором действительных значений. Частоты гармоник положительны. То, что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать».

3. Сигнал, измеренный на отрезке времени Т определен только на отрезке времени Т. Что было до того, как мы начали измерять сигнал, и что будет после того — науке это неизвестно. И в нашем случае — неинтересно. ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле, что при определенных условиях позволяет вычислить амплитуду и частоту его составляющих.

Использованные материалы и другие полезные материалы.

FourierScope — программа для построения радио сигналов и их спектрального анализа.
Graph — программа с открытым кодом, предназначенная для построения математических графиков.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ – КАК ЭТО ДЕЛАЕТСЯ
Дискретное преобразование Фурье (ДПФ)