Почему умножение матриц такое / forpes.ru

Главная
Почему умножение матриц такое

Почему умножение матриц такое +67

30.11.2022 21:02

Monotirg 89 28000 Источник

Наверное, каждый задавался вопросом, почему умножение матриц такое. В этой статье мы разберём из каких соображений оно вводится именно так.

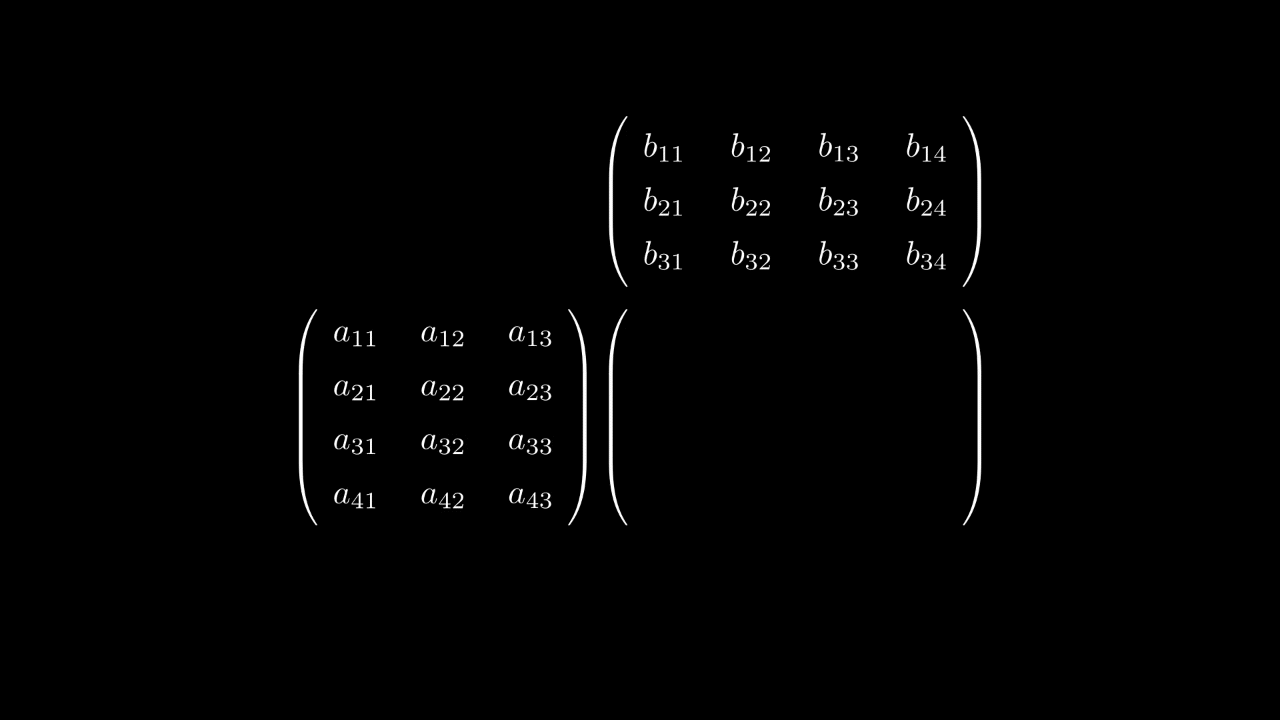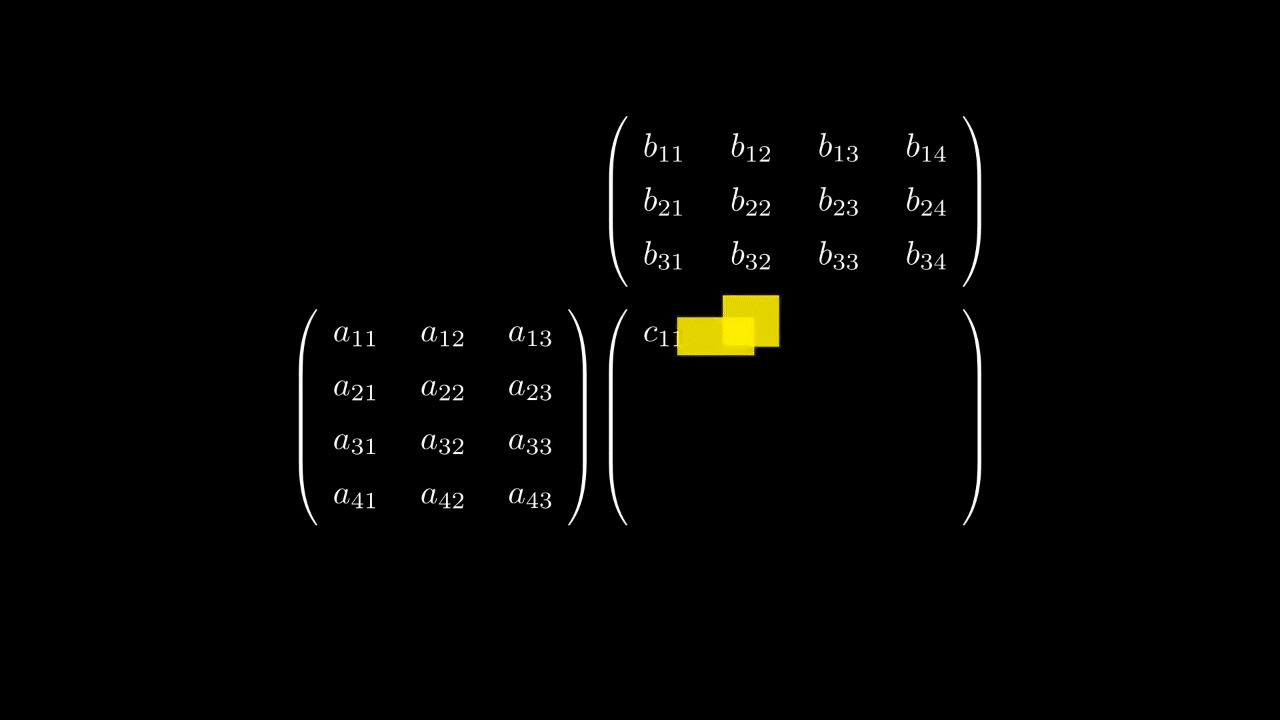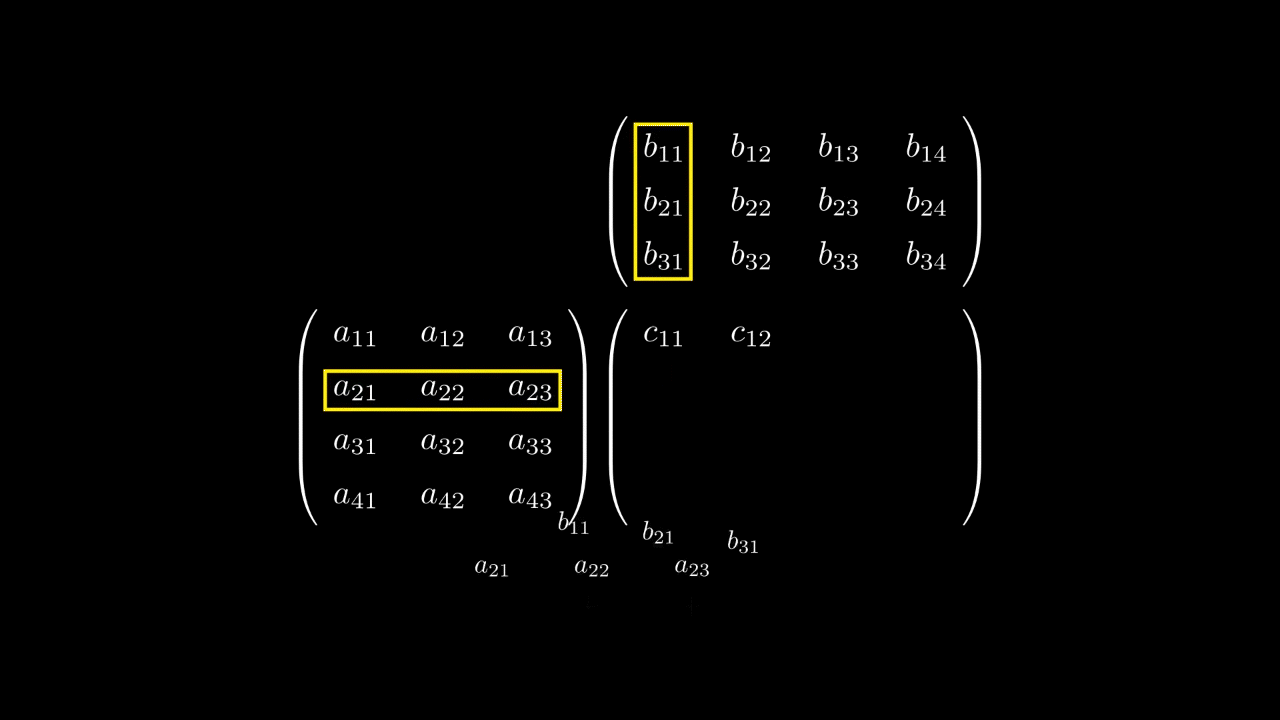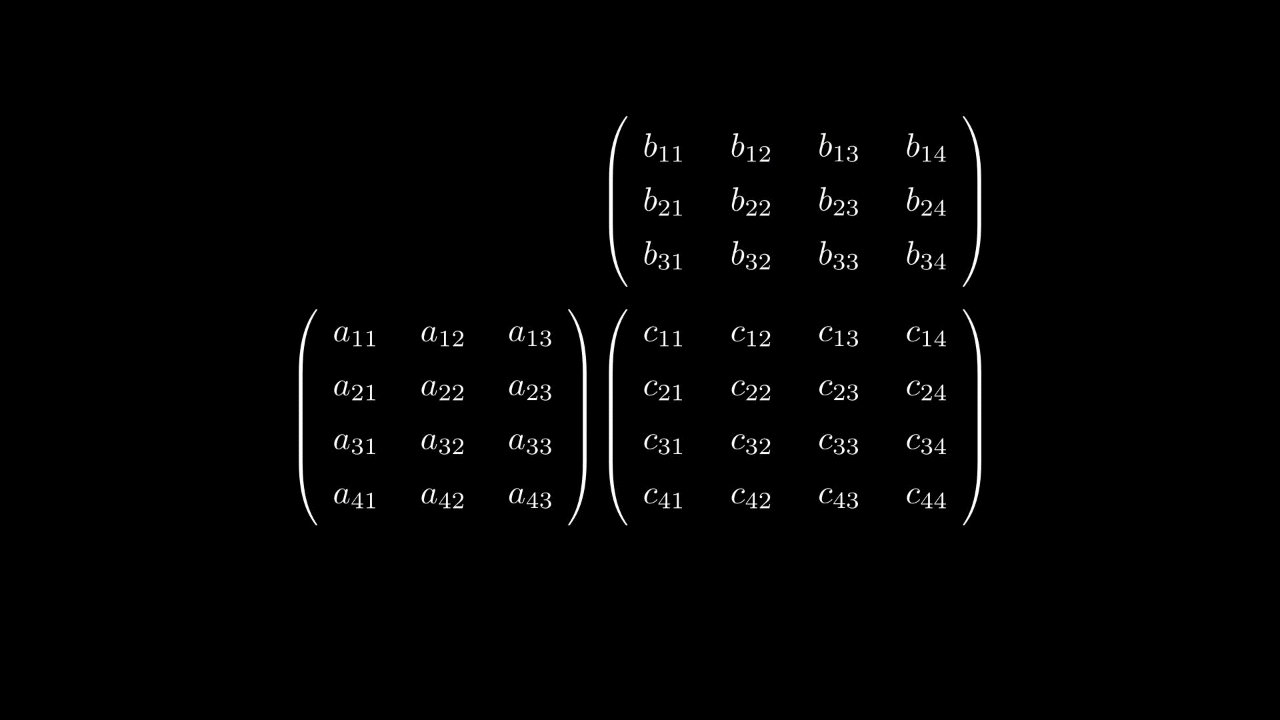
Маленькое предисловие

В дальнейшем нам понадобится такая структура, как векторное пространство, а точнее его частный случай $\mathbb{R}^n$ — пространство столбцов высотынад $\mathbb{R}.$ Кратко напомню, что под этим понимается.

Во-первых, $\mathbb{R}^n$ — это следующее множество

$\mathbb{R}^n=\{[x_1,\ldots,x_n] \,|\,x_i\in\mathbb{R}\},$

где таким образом $[x_1,\ldots,x_n]$ обозначен вектор-столбец высотыто есть

$[x_1,\ldots,x_n]=\left(\begin{array}{c} x_1 \\ \vdots \\ x_n \end{array}\right).$

Во-вторых, для любых векторов $x,y \in \mathbb{R}^n$ определено сложение

$x+y = [x_1,\ldots,x_n]+[y_1,\ldots,y_n]=[x_1+y_1,\ldots,x_n+y_n]$

и для любого вектора $x \in \mathbb{R}^n$ определено умножение на скаляр $\lambda \in \mathbb{R}$

$\lambda x = \lambda[x_1,\ldots,x_n] = [\lambda x_1,\ldots,\lambda x_n].$

В-третьих, каждый вектор $x \in \mathbb{R}^n$ единственным образом представим в следующем виде

$x=x_1e_1+\ldots+x_ne_n,$

где $x_1,\ldots,x_n$ — скаляры, а $(e_1,\ldots,e_n)$ — следующая система векторов

$e_1=[1,0,\ldots,0],\,e_2=[0,1,\ldots,0],\ldots,\,e_n=[0,0,\ldots,1].$

Такая система векторов называется базис, а скаляры, участвующие в разложение вектора, называются координатами этого вектора в данном базисе. Стоит отметить, что в $\mathbb{R}^n$ это не единственный базис, но везде далее под «зафиксируем базис» можно понимать именно эту систему векторов.

Умножение матрицы на вектор

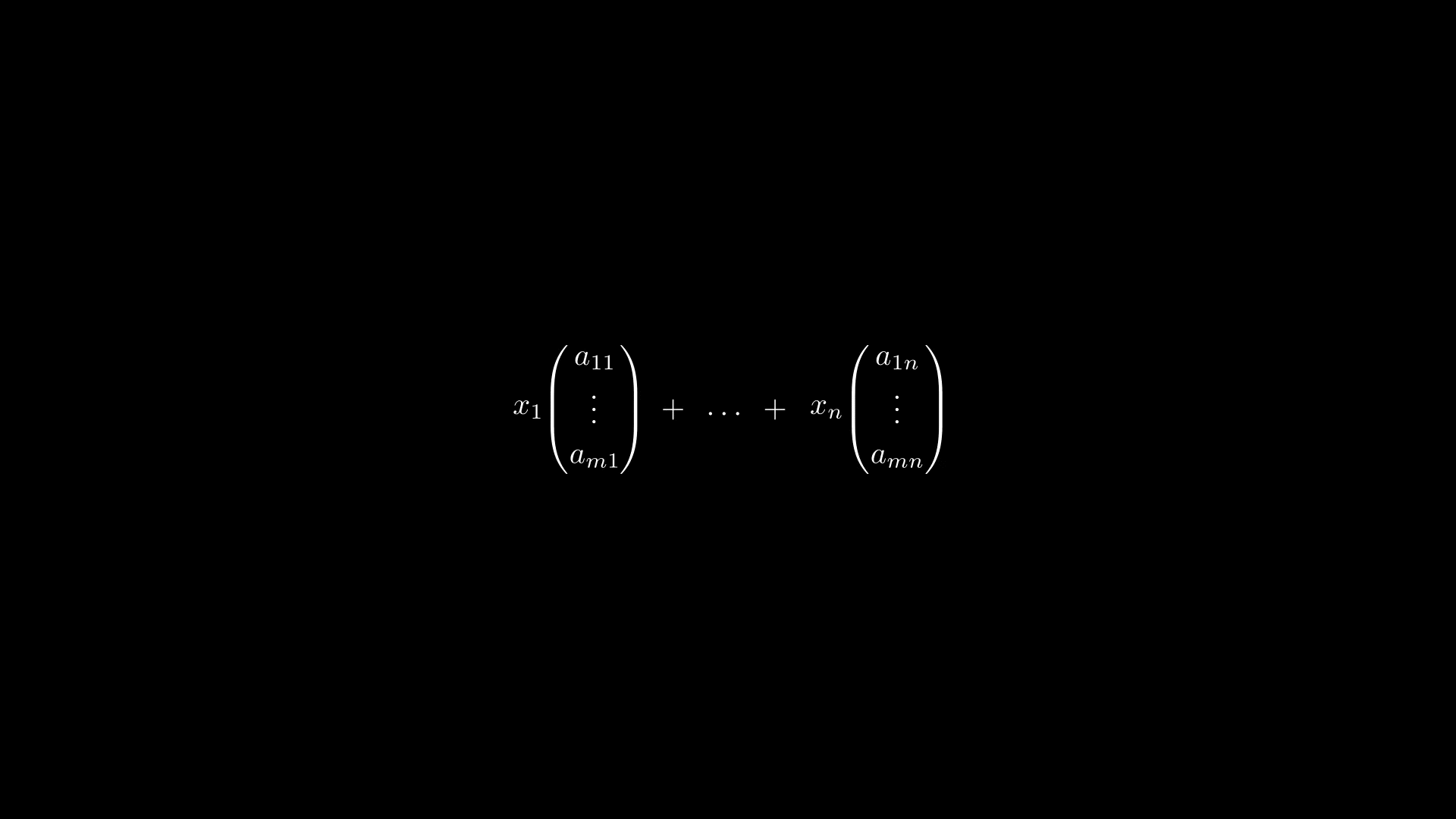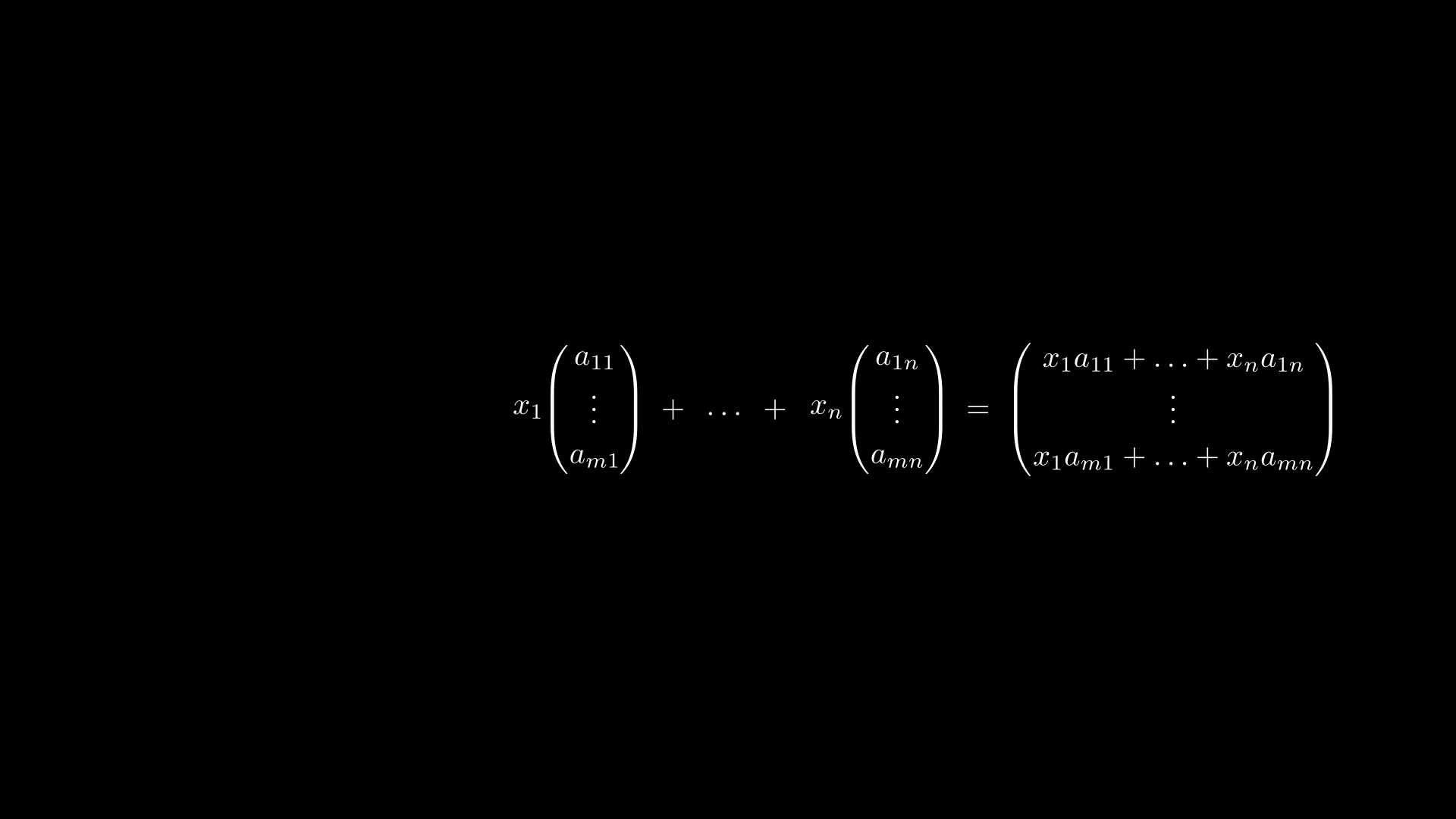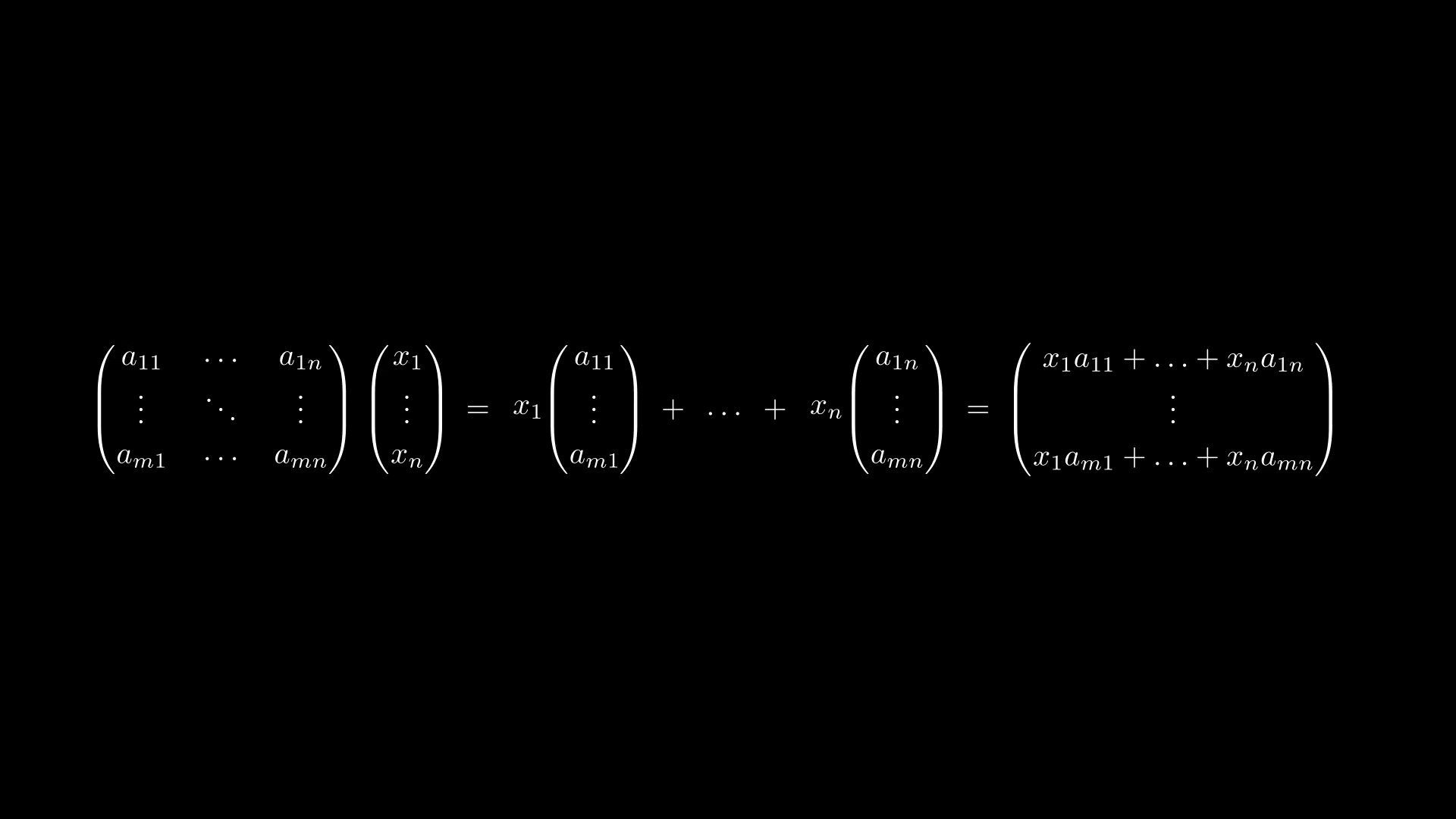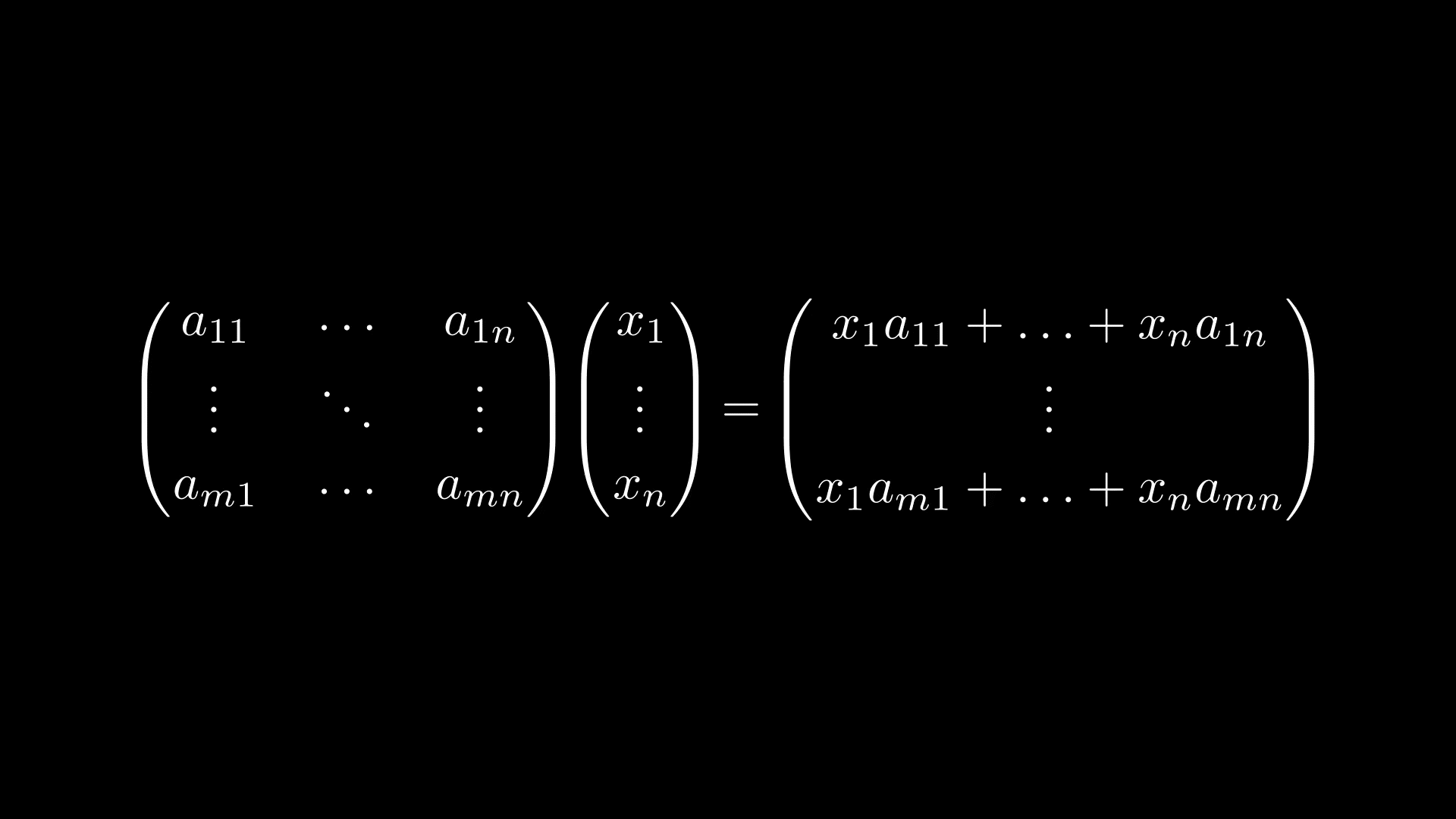
Прежде чем переходить к умножению матриц, посмотрим, из каких соображений вводится умножение матрицы на вектор. Для этого рассмотрим линейное отображение $\mathcal{A}$

$\mathcal{A}:\mathbb{R}^n \rightarrow \mathbb{R}^m.$

То, что $\mathcal{A}$ — линейное отображение, означает, что для любых векторов $x,y \in \mathbb{R}^n$ и любого скаляра $\lambda \in \mathbb{R}$ выполняются следующие два условия:

$\begin{array}{l} \mathcal{A}(x+y)=\mathcal{A}x + \mathcal{A}y.\\ \mathcal{A}(\lambda x)=\lambda\mathcal{A}x. \end{array}$

Или их можно объединить в одно

$\mathcal{A}(\lambda_1 x + \lambda_2 y)=\lambda_1\mathcal{A} x + \lambda_2 \mathcal{A}y.$

Нас интересует, как линейное отображение $\mathcal{A}$ действует на произвольный вектор $x \in \mathbb{R}^n.$ Для этого зафиксируем в $\mathbb{R}^n$ базис $(e_1,\ldots,e_n),$ а в $\mathbb{R}^m$ базис $(f_1,\ldots,f_m).$ Теперь мы можем разложить векторпо базису

$x = x_1e_1+\ldots+x_ne_n$

и представить $\mathcal{A}x$ в следующем виде

$\mathcal{A}x=\mathcal{A}(x_1e_1+\ldots+x_ne_n)=x_1\mathcal{A}e_1+\ldots+x_n\mathcal{A}e_n.$

Заметим, что $\mathcal{A}e_1,\ldots,\mathcal{A}e_n \in \mathbb{R}^m,$ а поскольку в $\mathbb{R}^m$ зафиксирован базис, то эти векторы также можно разложить по базису

$\mathcal{A}e_1 = a_{11}f_1+a_{21}f_2+\ldots+a_{m1}f_m, \\ \mathcal{A}e_2 = a_{12}f_1+a_{22}f_2+\ldots+a_{m2}f_m, \\ \ldots \\ \mathcal{A}e_n = a_{1n}f_1+a_{2n}f_2+\ldots+a_{mn}f_m.$

или тоже самое в векторной записи

$\begin{array}{cccc} \mathcal{A}e_1 = \left( \begin{array}{c} a_{11}\\ \vdots \\ a_{m1} \end{array} \right), & \mathcal{A}e_2 = \left( \begin{array}{c} a_{12}\\ \vdots \\ a_{m2} \end{array} \right), & \ldots &, & \mathcal{A}e_n = \left( \begin{array}{c} a_{1n}\\ \vdots \\ a_{mn} \end{array} \right) \end{array}.$

Подставляем в равенство выше и получаем

$x_1\mathcal{A}e_1+\ldots+x_n\mathcal{A}e_n= x_1 \left( \begin{array}{c} a_{11}\\ \vdots \\ a_{m1} \end{array} \right) + \ldots + x_n \left( \begin{array}{c} a_{1n}\\ \vdots \\ a_{mn} \end{array} \right) = \left( \begin{array}{c} x_1a_{11} + \ldots + x_na_{1n}\\ \vdots \\ x_1a_{m1} + \ldots + x_na_{mn} \end{array} \right)$

Но правая часть равенства есть не что иное, как формула умножения матрицы на вектор-столбец

$\left( \begin{array}{ccc} a_{11} & \ldots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \ldots & a_{mn} \end{array} \right) \left( \begin{array}{c} x_{1} \\ \vdots \\ x_n \end{array} \right),$

где столбцы матрицы есть векторы $\mathcal{A}e_1,\ldots,\mathcal{A}e_n$

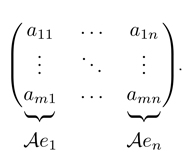
Получается, можно ввести умножение матрицы на вектор по следующему правилу

$\small \left( \begin{array}{ccc} a_{11} & \ldots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \ldots & a_{mn} \end{array} \right) \left( \begin{array}{c} x_{1} \\ \vdots \\ x_n \end{array} \right) = x_1 \left( \begin{array}{c} a_{11}\\ \vdots \\ a_{m1} \end{array} \right) + \ldots + x_n \left( \begin{array}{c} a_{1n}\\ \vdots \\ a_{mn} \end{array} \right) = \left( \begin{array}{c} x_1a_{11} + \ldots + x_na_{1n}\\ \vdots \\ x_1a_{m1} + \ldots + x_na_{mn} \end{array} \right).$

И такое определение умножения будет согласовано с тем, как линейное отображение $\mathcal{A}$ действует на вектор

Если теперь обозначить $y= \mathcal{A}x,$ то координаты вектора выражаются через координаты вектора следующим образом

$y_i = \sum_{i=1}^{n}a_{ij}x_j,\quad i = 1,\ldots,m,$

Кроме того, мы получили и другой важный результат, вернёмся к выражению для $\mathcal{A}x$

$\mathcal{A}x=\mathcal{A}(x_1e_1+\ldots+x_ne_n)=x_1\mathcal{A}e_1+\ldots+x_n\mathcal{A}e_n.$

Из него следует, что линейное отображение $\mathcal{A}$ полностью определяется своими значениями на базисных векторах, то есть, если нужно найти $\mathcal{A}x,$ то достаточно знать $\mathcal{A}e_1,\ldots,\mathcal{A}e_n.$

Далее, мы поместили эти векторы в матрицу и определили умножение так, что $\mathcal{A}x$ есть произведение соответствующей матрицынаПолучается, что линейному отображению можно поставить в соответствие матрицу, которая полностью его определяет

$\forall x \in \mathbb{R}^n: \mathcal{A}x = Ax.$

Такая матрица называется матрицей линейного отображения $\mathcal{A}$ в выбранных базисах пространств $\mathbb{R}^n$ и $\mathbb{R}^m.$

Если говорить более строго, то существует взаимно однозначное соответствие между линейными отображениями из $\mathbb{R}^n$ в $\mathbb{R}^m$ и матрицами размера $m \times n.$

Теперь мы можем перейти к умножению матрицы на матрицу.

Умножение матрицы на матрицу

Рассмотрим линейные отображения $\mathcal{A}$ и $\mathcal{B}$

$\mathcal{A} : \mathbb{R}^m \rightarrow \mathbb{R}^s, \quad \mathcal{B} : \mathbb{R}^n \rightarrow \mathbb{R}^m,$

и их композицию $\mathcal{C}$

$\mathcal{C} = \mathcal{A} \circ \mathcal{B}.$

Легко проверяется, что $\mathcal{C}$ будет линейным отображением

$\mathcal{C}(\lambda_1x+\lambda_2y)= (\mathcal{A} \circ \mathcal{B})(\lambda_1x+\lambda_2y)= \mathcal{A}(\mathcal{B}(\lambda_1x)+\mathcal{B}(\lambda_2y))=\mathcal{A}(\lambda_1\mathcal{B}x+\lambda_2\mathcal{B}y)= \\ = \lambda_1\mathcal{A}(\mathcal{B}x)+\lambda_2\mathcal{A}(\mathcal{B}y)=\lambda_1\mathcal{C}x+\lambda_2\mathcal{C}y.$

Поэтому, если зафиксировать в $\mathbb{R}^n, \mathbb{R}^m$ и $\mathbb{R}^s$ базисы, то каждому линейному отображению можно поставить в соответствие его матрицу

$\mathcal{A} \mapsto A, \quad \mathcal{B} \mapsto B, \quad \mathcal{C} \mapsto C.$

Нас теперь интересует, как между собой они связаны. Для этого рассмотрим следующее равенство

$(\mathcal{A} \circ \mathcal{B})x =\mathcal{A}(\mathcal{B}(x)) = \mathcal{A}y = z$

и найдём координаты вектора через координаты вектора

Так как $\mathcal{A}y=z,$ то

$z_i=\sum_{k=1}^{m}a_{ik}y_k, \quad i =1,\ldots,s.$

Но из равенства $y= \mathcal{B}x$ следует, что

$y_k=\sum_{j=1}^{n}b_{kj}x_j, \quad k = 1,\ldots,m.$

Подставляем в равенство выше и получаем

$z_i=\sum_{k=1}^{m}a_{ik}y_k= \sum_{k=1}^{m}a_{ik}\sum_{j=1}^{n}b_{kj}x_j=\sum_{j=1}^{n}(\sum_{k=1}^{m}a_{ik}b_{kj})x_j, \quad i =1,\ldots,s.$

С другой стороны, $(\mathcal{A} \circ \mathcal{B})x = \mathcal{C}x=z,$ то есть

$z_i= \sum_{j=1}^{n}c_{ij}x_j, \quad i = 1,\ldots,s.$

Сравнивая первое и второе равенство для координатполучаем такое соотношение

$c_{ij}=\sum_{k=1}^{m}a_{ik}b_{kj} \quad (i=1,\ldots,s;\,j=1,\ldots,n),$

которое является формулой умножения матрицы на матрицу.

Таким образом, умножение матрицы на матрицу вводится исходя из того, как действует композиция линейных отображений.

Другими словами, если линейным отображениям $\mathcal{A}$ и $\mathcal{B}$ поставить в соответствие их матрицыито композиции этих отображений $\mathcal{A} \circ \mathcal{B}$ ставится в соответствие матрица, которая является произведением матриц

Отсюда, кстати, следует, что матрицыиможно умножить только тогда, когда число столбцов матрицыравно числу строк матрицы

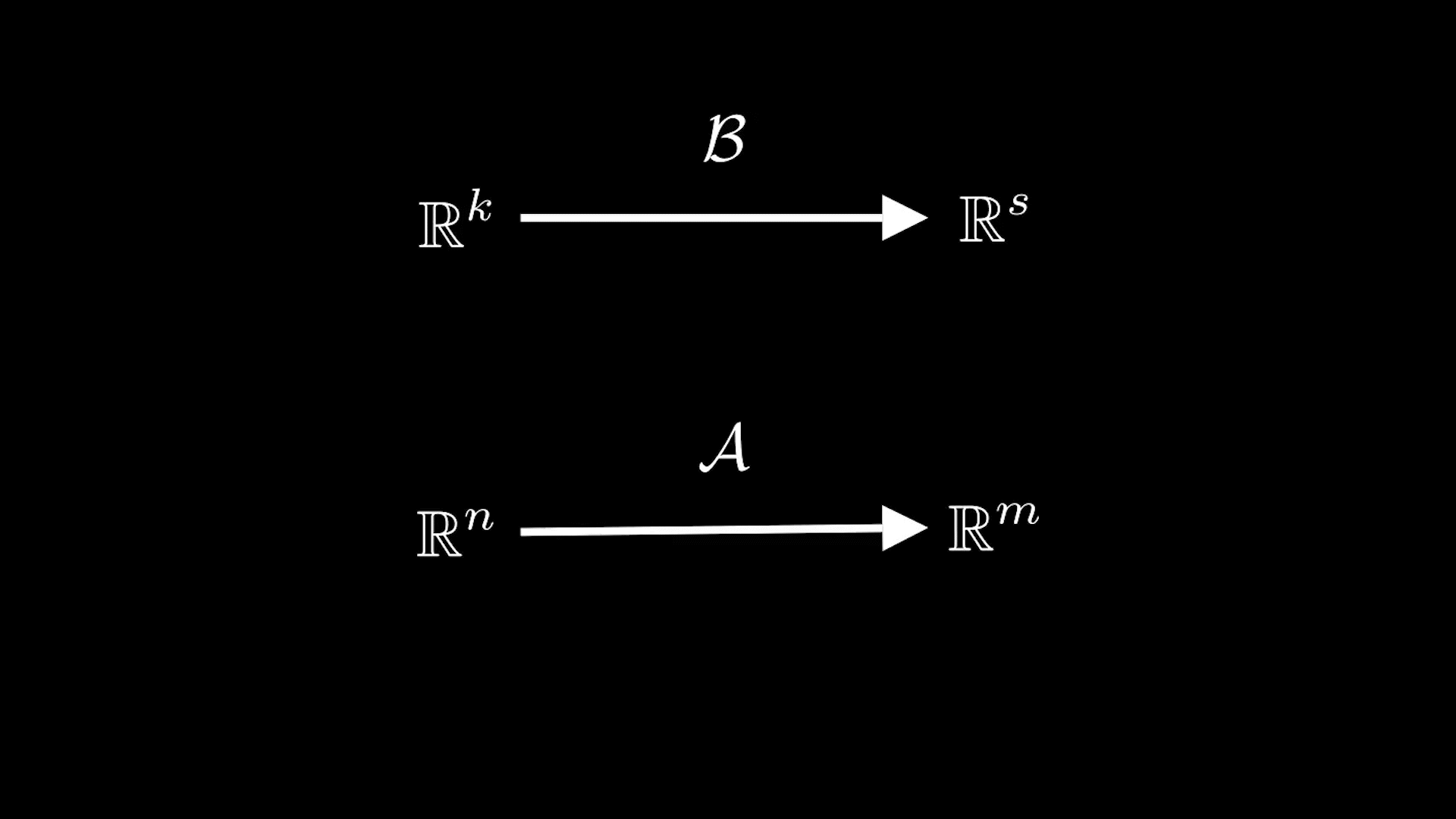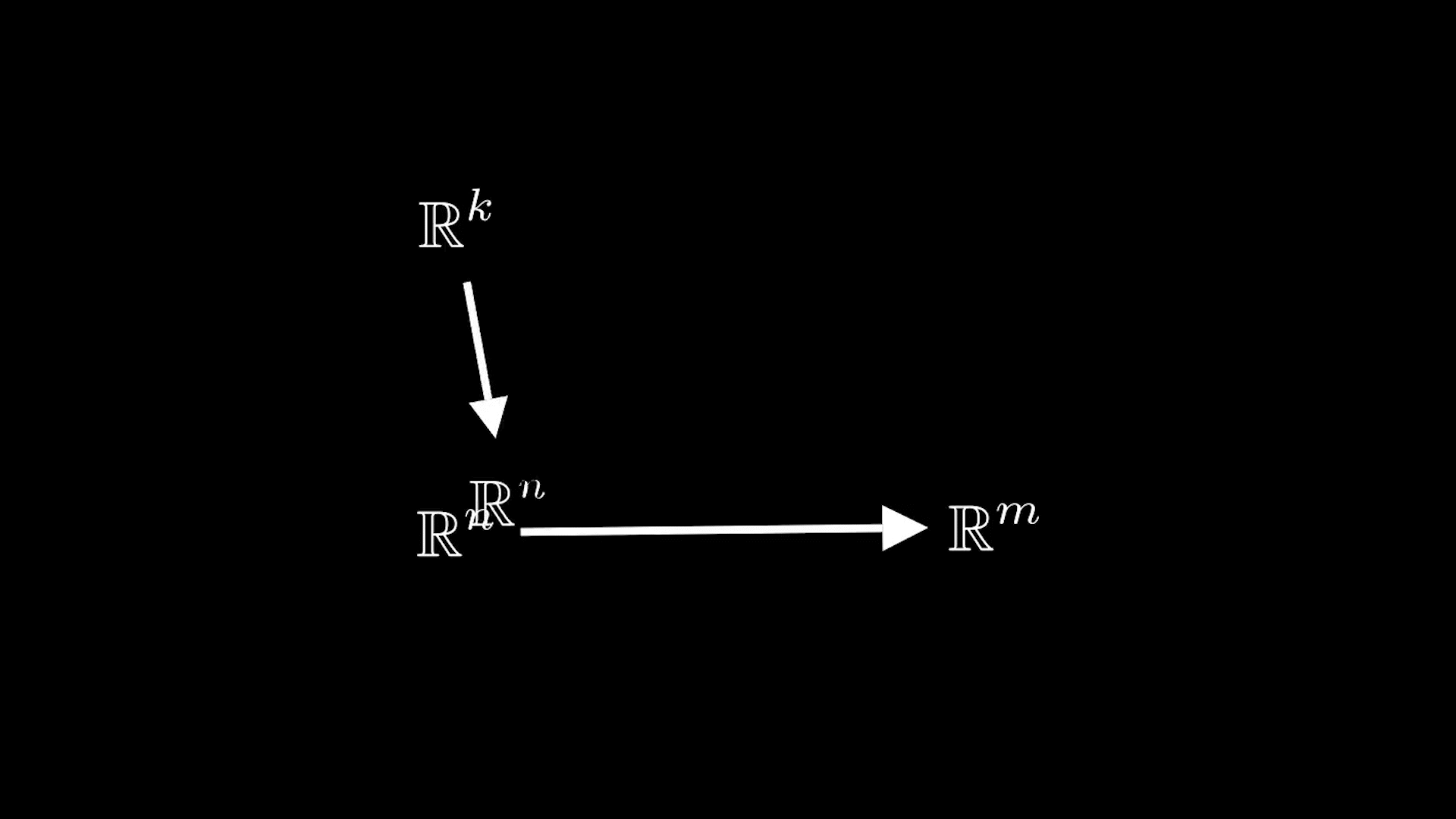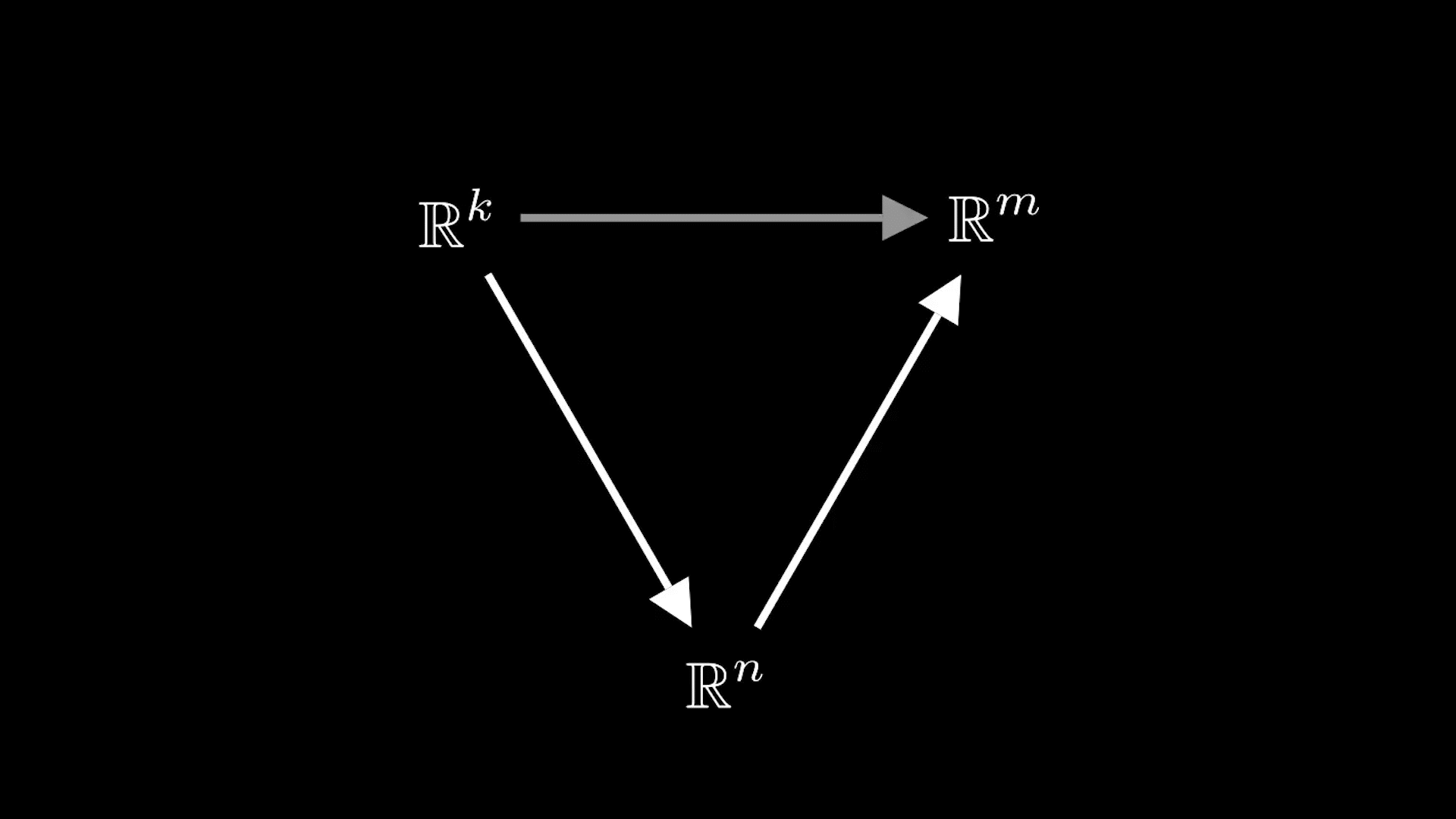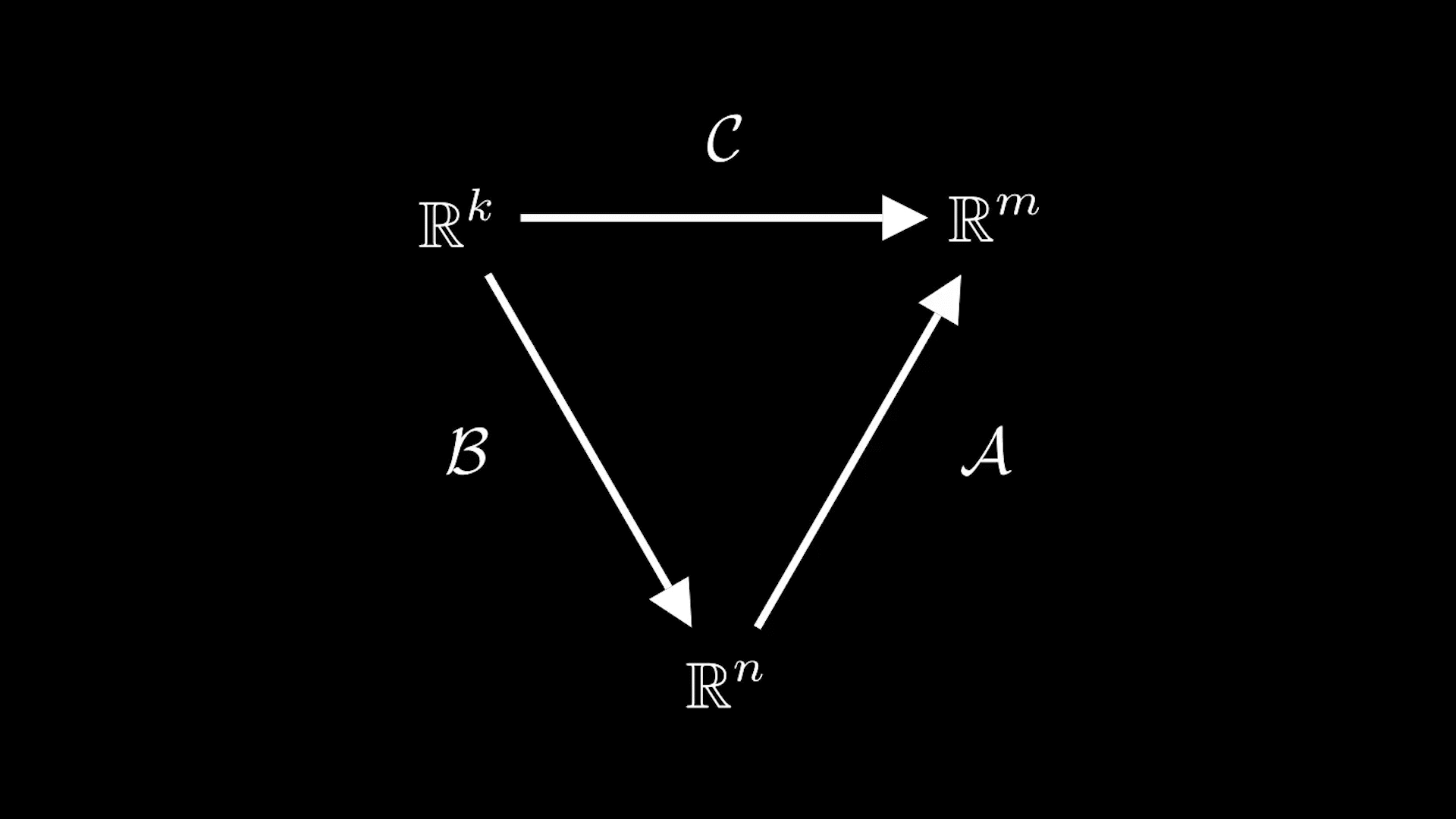
Пусть — матрица размера $m \times n,$ а — матрица размера $s\times k.$ Тогда, если в пространствах $\mathbb{R}^n,\mathbb{R}^m,\mathbb{R}^k$ и $\mathbb{R}^s$ зафиксировать базисы, то этим матрицам ставятся в соответствие линейные отображения $\mathcal{A}$ и $\mathcal{B}$

$\mathcal{A}:\mathbb{R}^n \rightarrow \mathbb{R}^m,\quad \mathcal{B}: \mathbb{R}^k \rightarrow \mathbb{R}^{s}.$

Но композиция $\mathcal{A} \circ \mathcal{B}$ определена только тогда, когда то есть число столбцов матрицыравно числу строк матрицы

Заключение

Таким образом, умножение матриц вводится исходя из того, как действуют линейные отображения. И это намекает на некую связь между ними.

Ниже оставлю различные учебники по алгебре, где можно про всё это прочитать более подробно, и другие различные источники.

Ссылки на литературу и различные источники

Основное:

[1] Введение в алгебру. В 3 частях. Часть 1. Основы алгебры. Кострикин А.И.

Дополнительное:

[1] Введение в алгебру. В 3 частях. Часть 2. Линейная алгебра. Кострикин А.И.

[2] Линейная алгебра и геометрия, Кострикин А.И., Манин Ю.И.

Прочее:

Для создания графики использовался manimCE: https://github.com/manimCommunity/manim

Кому интересно, то вот видео к статье:

Комментарии (89)

tempick
30.11.2022 22:13
#24966590
+18
Мне больше понравилось вот это видео, и в целом был интересен весь плейлист:
1. stanislavskijvlad
  01.12.2022 10:48
  #24967726
  Можно ссылку текстом, пожалуйста. А то здесь белое ничто.
  1. playermet
    01.12.2022 12:01
    #24967964
    +4
    Видео выше: https://www.youtube.com/watch?v=tnjBY4Yq6mY
    
    Оригинал на английском: https://www.youtube.com/watch?v=XkY2DOUCWMU
1. rukhi7
  01.12.2022 15:50
  #24968766
  +1
  Да и здесь мультфильмы тоже вполне себе ничего.
  
  Интересно посмотреть сколько кода (текста) требуется чтобы "нарисовать" такой мультфильм. Ждем статью посвященную рисованию-кодированию-creating mathematical animations!
  1. Un_ka
    01.12.2022 17:20
    #24969144
    +2
    Такие статьи уже есть:
    
    https://habr.com/ru/company/skillfactory/blog/556944/
    
    https://habr.com/ru/company/yandex_praktikum/blog/578910/
    
    rukhi7
    01.12.2022 21:46
    #24969964
    Интересно! Надо попробовать сделать такую штуку на WPF, можно будет сравнить реализации.

MechanicusJr
30.11.2022 22:39
#24966668
+1
это все прекрасно и в ИТ используется, как и физика ..

хотя тут уже были статьи про Эйнштен неправ, и про успехи
1. Terimoun
  01.12.2022 00:10
  #24966834
  +1
  ИТ без математики никуда, да.
  1. Format-X22
    01.12.2022 00:21
    #24966858
    +24
    Это смотря без какой именно области, потому что, так то, много где никуда, даже хлеба не купишь, но если брать типичный энтерпрайз и кодирование бизнес-логики, даже если это биг дата и хайлод, не такая и большая область требуется. И даже в 3д играх тоже, если ты не с нуля пишешь. Чрезмерно переоценивать требование тоже не стоит, как бы романтично не хотелось бы в это верить.
    
    kenoma
    01.12.2022 16:30
    #24968922
    +1
    Образ мышления и способность вникать в сложные конструкции радикально отличаются у тех кто умеет и кто не умеет в матан. Те же паттерны проектирования, без которых в энтерпрайзах никуда, почему-то сложнее даются чистым гуманитариям, решившим в айти.
    
    Prion
    01.12.2022 19:39
    #24969606
    +1
    в общей массе программистов, особенно среди разработчиков сайтов, какая доля подобных программистов? вопрос стоит не в том нужен ли матан вообще, а в том, нужен ли он всем?
  1. Prion
    01.12.2022 15:29
    #24968650
    +2
    Вы это скажите миллионам айтишникам в том числе без высшего образования (либо с высшим и каким нибудь гуманитарным) которые клепают сайт и приложения на коленке.
1. funca
  01.12.2022 01:15
  #24966964
  +2
  Ссылки на литературу и различные источники
  
  Да, интересно как много тут людей, у которых все эти ссылки подсвечены фиолетовым?

Daddy_Cool
01.12.2022 00:42
#24966906
+3
Интересная статья, но с названием по-моему дело обстоит проще, нам нужна вот такая операция - давайте назовем её умножением матриц. А то почему бы матрицы не "умножать" по рабоче-крестьянски типа c11=a11*b11, c12=a12*b12, и т. д... )))
1. SteamEngine
  01.12.2022 00:45
  #24966918
  +15
  Не по-рабочекрестьянски, а по-адамаровски...
1. nmrulin
  01.12.2022 00:51
  #24966926
  См. комментарий от 0:44 , если как вы будете умножать , то мы не получим из вектора X вектор Z как мы изначально хотели.
  1. Daddy_Cool
    01.12.2022 02:43
    #24967080
    +10
    ...И ничего страшного! Получим что-то другое. Я вот вовсе не хотел из вектора X получать вектор Z. ))) Я в том смысле, что в начале идет необходимость в чем-то, а потом придумывается название этому.
    
    nmrulin
    01.12.2022 14:40
    #24968488
    Так я не против . Можно умножать как угодно лишь бы такая модель нашла потом применение на практике . Традиционный метод позволяет создать наибольшее число таких математических моделей.
1. funca
  01.12.2022 01:23
  #24966988
  +8
  А то почему бы матрицы не "умножать" по рабоче-крестьянски типа
  
  Тогда бы умножение матриц стало коммутативным и доступным для понимания даже школьникам начальных классов. Преподаватели в универах останутся без работы.
  1. Daddy_Cool
    01.12.2022 02:46
    #24967082
    +2
    Ну там рядом торцевое произведение притулилось.
    https://ru.wikipedia.org/wiki/Произведение_Адамара
1. wataru
  01.12.2022 14:34
  #24968470
  Можно определять умножение, как вам угодно. Но вот такое, как стандартно принято, обладает всякими полезными свойствами (вроде как указанного в статье вычисления матрицы комбинированного линейного преобразования). Еще эта операция обладает всякими привычными свойствами умножения (вроде дистрибутивности со сложением и ассоциативности). Поэтому именно эта операция и считается умножением. Так удобно.
  1. 0xd34df00d
    01.12.2022 18:40
    #24969448
    +1
    Наверное, логичнее было бы назвать её композицией матриц, потому что она напрямую отражает композицию линейных операторов.
    
    wataru
    01.12.2022 22:07
    #24970030
    Возможно. Но тогда все равно хотелось бы ввести какое-то умножение матриц, да еще так, чтобы от него какая-то польза была. А почленное умножение не позволяет столько классных штук делать. Например, решать линейные уравнения.
    
    0xd34df00d
    01.12.2022 22:14
    #24970056
    +1
    Зачем? Умножение строк же вам не хочется ввести?
    
    wataru
    01.12.2022 22:35
    #24970134
    Ну так и сложения строк как такового нет. А вот всякие алгебраические структуры по аналогии с числами привычно складывать и умножать.
    
    0xd34df00d
    01.12.2022 23:27
    #24970260
    +1
    Но строки — это как раз канонические алгебраические структуры! В смысле, строка над алфавитом A — это свободный моноид (или свободная группа, если добавить для каждого символа «обратный символ») над алфавитом A.
    
    wataru
    02.12.2022 13:01
    #24971540
    Ну и где там про сложение строк? Но вообще, я уверен, что есть какая-то очень абстрактная теория, где над чем-то, на что можно натянуть термин "строка", можно проивзодить операцию, которую называют "сложением".
    
    Но сколько-нибудь распространенной операция сложения на строках не является. Потому что там аналогии со сложением чисел не получается. Ибо как произвольную строку вычесть из произвольной сторки? Именно поэтому в теории формальных языков строки конкатенируют, а не складывают. Если бы операция была похожа на сложение, его бы для удобства восприятия так и назвали.
    
    0xd34df00d
    02.12.2022 17:55
    #24972970
    +1
    А натуральные числа вы складываете или что вы с ними делаете?
    
    wataru
    02.12.2022 18:20
    #24973042
    Да, складываю. Я правда не понимаю, что к чему вы клоните? Натуральные числа — это частный случай строк? Ну тогда ваш изначальный вопрос снимается:
    
    Зачем? Умножение строк же вам не хочется ввести?
    
    Умножение "строк" тогда уже есть — умножение натуральных чисел.
    
    Мое утверждение, что раз есть сложение, то логочно и умножение ввести по аналогии с числами — не опровергнуто.
    
    0xd34df00d
    02.12.2022 18:39
    #24973124
    +1
    Да, складываю. Я правда не понимаю, что к чему вы клоните?
    
    Ну, получается, чтобы назвать операцию сложением, вычитать уметь не обязательно. Два произвольных натуральных числа вы вычесть тоже не можете.
    
    Натуральные числа — это частный случай строк?
    
    Кстати, да. Можно (но не то чтобы нужно) рассмотреть свободный моноид над алфавитом из одного символа. Между этим моноидом и натуральными числами будет очевидный моноидальный гомоморфизм (который даже изоморфизм).
    
    Умножение "строк" тогда уже есть — умножение натуральных чисел.
    
    Умножение строк над алфавитом из одного символа, да, так можно определить. Но как его доопределить до умножения на произвольном алфавите?
    
    wataru
    02.12.2022 18:46
    #24973146
    Ну, получается, чтобы назвать операцию сложением, вычитать уметь не обязательно. Два произвольных натуральных числа вы вычесть тоже не можете
    
    Ну, более чем в половине случаев — вычитать можно. Со строками же все гораздо хуже.
    
    0xd34df00d
    02.12.2022 23:55
    #24973782
    ИМХО это уже какое-то натягивание совы из определений на глобус, но ваш поинт я понял, хотя и не могу с ним согласиться.
1. Survtur
  01.12.2022 21:17
  #24969792
  +1
  Угу. Мне вот очень не нравится, что умножением иногда называют операции, в которых А*В != В*А. Назвали бы как-то иначе. Ну не знаю, трансплюкированием.

nmrulin
01.12.2022 00:44
#24966914
+35
По мне очень математически описано, чтобы понять статью надо врубиться в кучу новых терминов.

Тогда как на самом деле матрица исторически это запись системы уравнения

a11x1+a12x2+...=b1

a21x1+...=b2

...

Отсюда и правила по которым матрица A преобразует вектор X в вектор Y.

Пусть ещё есть матрица B , которая преобразует вектор Y в вектор Z.

Соответственно матрица A*B должна быть такая, чтобы сразу же преобразовать вектор X в вектор Z. Собственно всё.
1. punhin
  01.12.2022 14:34
  #24968468
  "матрица исторически это запись системы уравнений".
  
  Исторически - да, но сегодня в матрицы закладывается совершенно иной смысл, доводящий их до математической абстракции, в которой любое действие может иметь смысл (но его ещё нужно как-то понять). Без понимания сути выполняемых действий математика превращается в набор предметов, что-то вроде "линейной магии, высшей магии и основ магического анализа". Конечно, хочется понимать, что же ты делаешь, но, к сожалению, для непосвящённых математика всё больше превращается в религию с мистерией формул...
  1. oleg_rico
    01.12.2022 16:58
    #24969052
    +3
    Предлагаю вам понять комплексные числа и заодно мнимые числа вроде корня квадратного из -1.
    
    Математика - это прежде всего игра ума, абсолютная полная абстракция. А уже потом продукт этой самой игры ума приспосабливают для использования в каких-то практических целях. Но никак не наоборот.
    
    0xd34df00d
    01.12.2022 18:48
    #24969470
    +2
    А что там понимать? В зависимости от того, что удобнее — это либо напрямую описываемая соответствующая алгебраическая структура, либо фактор-кольцо многочленов над ℝ по идеалу, порожденному x² + 1, либо ещё как. Мне определение через фактор-кольцо кажется наиболее интуитивным (конечно, после того, как вы интернализировали понятие фактор-множества/группы/кольца/етц, но это на самом деле легко).
    
    nmrulin
    01.12.2022 23:44
    #24970296
    Ну обычные числа описывают предметы(здесь и сейчас). А комплексные - чаще всего процессы. Например колебания шарика на пружине можно представить как движение по кругу по двумя осям - действительной координате x. И мнимой координате y , которая пропорциональна скорости v.
    
    То есть мы сложный случай(процесс) выразили как простой(набор координат).
    
    "А уже потом продукт этой самой игры ума приспосабливают для использования в каких-то практических целях. Но никак не наоборот. " - ну почему Ньютон разработал дифференциальное исчисление конкретно под механические задачи. И в дальнейшем, в математике был например "Спор о струне" и т.д.

KvanTTT
01.12.2022 02:55
#24967086
-5
Вообще с матрицами можно делать все что угодно, с учетом того, что все функции раскладываются в ряд Тейлора.
1. Tiriet
  01.12.2022 04:15
  #24967132
  +9
  Функция Вейерштрасса не раскладывается в ряд Тейлора. функция модуля не раскладывается в ряд Тейлора в окрестности нуля. Вейвлеты высоких порядков не раскладываются в ряд Тейлора. Дельта-функция Дирака не раскладывается в ряд Тейлора в окрестности нуля.
  1. Refridgerator
    01.12.2022 07:19
    #24967262
    +1
    Попроще есть варианты — e^(-1/x²) в нуле тоже не раскладывается ряд Тейлора, хотя не имеет разрывов.
    
    Tiriet
    01.12.2022 08:27
    #24967340
    -3
    ? в окрестности нуля она прекрасно раскладывается в ряд Тейлора: exp(-1/(x*x)) = 0 (самый-самый простой и короткий ряд Тейлора- полином нулевого порядка!).
    
    в окрестности нуля x- бесконечно малая первого порядка, 1/x2- бесконечно большая второго порядка, exp(-1/(x*x))- бесконечно малая бесконечного порядка. в окрестности нуля ряд Тейлора нулевой, для любого eps>0 существует dx>0 такая, что |f(dx)-0|<eps.
    
    Refridgerator
    01.12.2022 08:48
    #24967388
    Не, ну если 0 рассматривать как ряд — то да, формально раскладывается. Но всё-таки степенной ряд — это ряд со степенями, задачей которого состоит аппроксимация функции. Из бесконечного ряда нулей исходную функцию не восстановишь. По вашей логике тогда и функция Вейерштрасса, и функция модуля, и даже функция знака тоже должны быть разложимы.
    
    Tiriet
    01.12.2022 12:24
    #24968058
    +2
    да, надо строже обращаться с терминами.
    
    функция разложима в ряд Тейлора в некоторой окрестности- это значит, что для функции этот ряд сходится и сходится именно к этой функции (с абсолютной точностью). как, например, summ(x^k)=1/(1-x)- это точное представление на интервале (-1..1)
    
    есть функции, которые с любой наперед заданной точностью на интервале могут быть аппроксимированы рядом Тейлора, но при этом ряд не сходится в точности к этой функции (как приведенная вами экспонента- она не аналитическая в нуле, хотя и абсолютно дифференцируема в нуле). Такие функции аппроксимируются частичным рядом Тейлора с погрешностью О(dx^k):
    
    f(x)= summ( a.i*x^i)[i=0..k-1] + O(x^k)
    
    а есть функции, которые и не раскладываются, и не аппроксимируются рядом Тейлора.
    
    Модуль недифференцируем в нуле, и потому в нуле в ряд Тейлора не раскладывается и не аппроксимируется (нет полиномиальной функции, имеющей погрешность порядка О(dx^k)- только О(1)), а в окрестности любой другой точки- раскладывается в ряд (то есть, может быть точно представлен рядом Тейлора). ф. Вейерштрасса вообще нигде не дифференцируема, и потому ни в какой точке не раскладывается в ряд Тейлора и не аппроксимируется рядом Тейлора, вейвлеты высоких порядков имеют локальную область поддержки, за пределами которой они нулевые, и потому раскладываются в ряд Тейлора в любой точке за пределами области поддержки, и не раскладываются и не аппроксимируются в ряд Тейлора ни в какой точке в области поддержки, ну и дельта-функция, как и модуль, разложима везде, кроме нуля.
    
    Refridgerator
    01.12.2022 13:34
    #24968310
    -1
    Я так и не понял, о какой разнице вы мне толкуете. Функцию модуля аналитически можно описать как sqrt(x^2) и по свойствам они ничем не будут отличаться. Её можно продифференцировать совершенно обычным стандартным образом — и получится функция x/sqrt(x^2), которая ничем не будет отличаться уже от функции знака (кроме точки 0, которая у функции знака принудительно доопределяется нулевым значением). Функция Вейерштрасса определяется в спектральном домене, и её в этом же спектральном домене можно совершенно легально продифференцировать. То, что после этого она перестанет сходиться во временном домене — так это проблема схождения, а не существования производной.
    
    Tiriet
    01.12.2022 14:43
    #24968506
    О_о. матанлиз все-таки строгая довольно дисциплина, там формулировки вылизаны до блеска, поэтому я и обратил Ваше внимание на разницу между " ф-я разложима в ряд Тейлора", "ф-я может быть аппроксимирована рядом Тейлора, но ряд не сходится к функции" и "ф-я не разложима и не может быть аппроксимирована рядом Тейлора"- это три сильно разных случая, и любой из них может реализовываться на всей оси, на отрезке или в точке.
    
    у функции модуля производная в нуле отсутствует, хоть как вы его через корни представляйте, поэтому в нуле она не разложима в ряд Тейлора, а в любой другой точке- разложима.
    
    Рассуждения про "проблема схождения, а не существования производной"- тоже весьма туманны, ряд Тейлора завязан на производную чуть менее, чем полностью, а производная- это предел отношения приращения функции к приращению аргумента в точке. У функции Вейерштрасса этот предел отсутствует в любой точке, поэтому ряд Тейлора для нее вообще нельзя построить, она не разложима и не может быть аппроксимирована ни с каким порядком точности, кроме нулевого. При чем тут "временные домены"? Дельта-функция или единичный скачок тоже во временном домене разложимы, только даже во временном домене для них ряды сходятся только в энергетической норме (L2), а в классическом смысле (в норме L1)- не сходятся, и ни дельта, ни скачок в норме L1 ни рядом Тейлора, ни рядом Фурье не аппроксимируются ни в какой окрестности нуля.
    
    Refridgerator
    01.12.2022 15:26
    #24968634
    Вы мне тут рассказываете про понимание математики, которое было ещё до появления комплексных чисел, не говоря уже об интеграле Фурье и функций Дирака с Хевисайдом. Математика 20-го века позволяет оперировать дискретными функциями как непрерывными, заодно расширяя понятия производной, позволяя ей иметь дробные порядки. С преобразованием Фурье функции Дирака тоже никаких проблем нет, степенной ряд соотносится с рядом Фурье через очевидную замену переменной, а сам степенной ряд можно рассматривать как частный случай z-преобразования, который допускает ещё и отрицательные значения степеней. Вся радио- и цифровая электроника строится на этом матаппарате.
    
    Tiriet
    01.12.2022 17:03
    #24969072
    Все мои рассуждения про сходимость ряда Тейлора в L1-норме остаются верными и для комплекснозначных функций комплексных аргументов (ибо теорема об аналитическом продолжении). Я прекрасно знаю, что ряд Фурье для единичного скачка элементарно вычисляется, но также я знаю, что в L1-норме он не сходится ни в вещественных числах, ни в комплексных- модуль погрешности ряда всегда остается порядка 9% от амплитуды скачка :-), и функция Вейерштрасса недифференцируема нигде, хотя и легко представима, как Вы выразились, во временном домене (как и вейвлеты Добеши, кстати). Собственно, поэтому я Вам и говорю, что в матанализе надо строго с терминами себя вести- там таких нюансов на каждом шагу по ведерку.
    
    Refridgerator
    01.12.2022 09:29
    #24967468
    -1
    Возможно не совсем очевидно, что при попытке разложения будет получаться 0+0·x+0·x²+0·x³+0·x⁴+…
    
    mayorovp
    01.12.2022 15:19
    #24968608
    Эдак можно и про функцию f(x)=0 написать, что она в ряд Тейлора не раскладывается...
    
    Refridgerator
    01.12.2022 15:45
    #24968742
    -1
    А где у вас в определении функции 0 x, то бишь аргумент? Так можно любое число назвать функцией. Ну и матрицей тоже можно назвать, 1x1. Ну и тензором тоже можно, чё мелочиться.
    
    mayorovp
    01.12.2022 15:51
    #24968768
    +3
    Назвать число функцией — для, нельзя. Но вот сопоставить каждому числу функцию, которая возвращает только его — без проблем можно.
    
    Точно так же как можно составить вектор, матрицу или тензор из одного элемента.
    
    Вы ещё скажите, что ноль не является вещественным числом, потому что у него нет дробной части.
    
    Refridgerator
    01.12.2022 16:05
    #24968814
    -1
    Я скажу, что не нужно менять причину и следствие. Функция конечно же может выродиться в константу, но для этого она должна быть сначала определена.
    
    mayorovp
    01.12.2022 16:11
    #24968842
    +1
    Кому должна?
    
    Функция, она же отображение — это правило, сопоставляющее каждому элементу из одного множества элемент из другого множества. Чем правило "любому элементу сопоставляется 0" хуже любого другого?
    
    Refridgerator
    01.12.2022 16:26
    #24968896
    -3
    Должна по определению. Правило «любому элементу сопоставляется 0» хуже любого другого тем, что оно необратимо и по смыслу мало отличается от выражений типа 0+0*0=0 с помощью которых доказываются равенства 2*2=5. И мне кажется, что графики моей и вашей функций таки заметно различаются, в отличие от разницы между abs(x) и sqrt(x*x), которую та же Mathematica регулярно использует в вычислениях. Так-то функция модуля для комплексного числа и определена через квадратный корень.
    
    mayorovp
    01.12.2022 17:55
    #24969280
    Должна по определению.
    
    Согласно общепринятому определению — не должна.
    
    Правило «любому элементу сопоставляется 0» хуже любого другого тем, что оно необратимо
    
    Обратимость — свойство биекции, от функции в общем случае не требуется быть обратимой.
    
    И мне кажется, что графики моей и вашей функций таки заметно различаются
    
    Так что, всё-таки функция, если у неё даже график построить можно?
    
    0xd34df00d
    01.12.2022 18:57
    #24969498
    +1
    Обратимость — свойство биекции
    
    В данном случае — инъекции. Сюръективность (или обратимость обратной функции, что в данном случае то же самое) тут не нужна.
    
    Refridgerator
    01.12.2022 22:26
    #24970106
    -1
    Товарищи минусующие. Я правильно понял, что определение модуля комплексного числа через корень — ошибочно, определение действительного числа как частного случая комплексного с нулевой мнимой составляющей — ошибочно, а умножение на ноль обратимо? Тогда расскажите пожалуйста, как правильно, а заодно и как правильно делить на ноль, чтобы получить исходное число или функцию.
    
    0xd34df00d
    01.12.2022 23:33
    #24970278
    +2
    определение действительного числа как частного случая комплексного с нулевой мнимой составляющей — ошибочно
    
    Не ошибочно, но методологически неправильно, потому что, похоже, проще всего строить алгебру, начиная с натуральных чисел, пополняя их до целых, затем до рациональных, затем до вещественных, а затем до комплексных. В обратную сторону идти как-то ИМХО сложнее.
    
    Минусы не ставил.
    
    Refridgerator
    02.12.2022 06:31
    #24970556
    Мне кажется более методологически неправильно превращать математику в религию в ущерб её прямому назначению — решение задач. Если моя, чисто практическая задача звучит как «найти минимум двух комплексных чисел» — то её нужно решить вне зависимости от того, определён порядок у комплексных чисел или нет. Или если во время численных вычислений требуется деление на ноль — это тоже нужно как-то решать. Это только в частных случаях типа sin(x)/x можно захардкодить проверку на abs(x)<eps и подсунуть заранее посчитанное значение.
    
    Я не вижу никакой проблемы отталкиваться от действительных чисел. Пространство интуитивно воспринимается скорее как непрерывное, а не дискретное, и понимание числа как «позиция» вполне согласуется с жизненным опытом. Согнутая в форме лука палка вполне согласуется с понятием «функция», которая непрерывна изначально, а не появляется из бесконечного количества бесконечно малых элементов. Комплексные числа вполне логично воспринимаются при переходе с линейки на миллиметровую бумагу. Часы со стрелками наглядно показывают умножение комплексных чисел, а заодно и переход на модульную арифметику, где количество возможных чисел ограничено.
    
    0xd34df00d
    02.12.2022 18:28
    #24973074
    +2
    Если моя, чисто практическая задача [...]
    
    Тогда вам на самом деле плевать, определять вещественные как частный случай комплексных, или комплексные выводить из вещественных.
    
    Мне кажется более методологически неправильно превращать математику в религию в ущерб её прямому назначению
    
    Если вы говорите о религии в смысле строгости, то есть риск получить всяких брадобреев, если забить на строгость.
    
    Refridgerator
    03.12.2022 11:39
    #24974542
    -1
    Я говорю, что если знание всех этих строгих формулировок не помогает решать задачи, а мешает этому - то ценность такого знания чуть меньше нуля по модулю. А также то, что качественное развитие математики так и просходило - когда кто-то начинал сомневаться в однозначности этой строгости.
    
    Refridgerator
    03.12.2022 11:45
    #24974556
    -1
    Парадокс брадобрея кстати разрешается элементарно, а заодно показывает ограниченность бинарной логики.
    
    Refridgerator
    03.12.2022 12:33
    #24974676
    -1
    Компилятор из описания var x=0 скорее выведет тип int, чем указатель на функцию возвращающую 0 типа real.
    
    mayorovp
    03.12.2022 12:52
    #24974726
    А из описания var f = x => 0 он выведет скорее функцию чем тип int. Но при чём тут вообще компилятор?
    
    Refridgerator
    03.12.2022 13:12
    #24974768
    -1
    А затем оптимизатор эту функцию вообще выкинет, как и все ссылки на неё. Вот и получится, что определить функцию вы попытались, но в исходном коде её почему-то не оказалось. При чём тут компилятор? Ну я хз, что на форуме математиков делают программисты.
    
    mayorovp
    03.12.2022 13:59
    #24974868
    Оптимизатор может что угодно выкинуть, включая программу целиком. Это вообще не аргумент.
    
    Refridgerator
    03.12.2022 16:54
    #24975176
    -1
    Это был ваш аргумент, а не мой. Спор был вообще о том, почему оппонент считает свои функции неразложыми, а мои - разложимыми, хотя они имеют один и тот же вид 0+остаточный член. Вы же привели 0 как функцию, у которой остаточный член тоже равен 0 и это доказывает мою неправоту, а ещё больше доказывает мою неправоту возможность записать этот ноль как вещественный тип, но без указания десятичной точки. Вероятно, проблемы нулей вам интереснее, чем неразложымые в ряд функции, но мне не сложно поддерживать и эту ветку обсуждения.
    
    0xd34df00d
    01.12.2022 18:55
    #24969484
    +1
    Так можно любое число назвать функцией.
    
    Можно, в Finord так и делают (если выкидывать из метатеории теорката объекты и рассматривать только стрелки, подразумевая под объектом его единицу).
    
    Refridgerator
    01.12.2022 21:42
    #24969944
    -2
    Да. В моей реализации dataflow-диаграмм (на c++ и c#) константа — это тоже функция. Но только потому, что там вообще всё — функция. Если например рассматривать константу «пи» как выражающую отношение длины окружности к длине её диаметра — то она равна 3.14… только в случае окружности на плоскости. В общем случае, для произвольной поверхности — эти значения будут отличаться.
    
    Что касается аппроксимации произвольной функции многочленом через разложение в степенной ряд — это прежде всего алгоритм, гарантирующий совпадение n-первых производных. Получить аппроксимацию функции многочленом можно и другими способами, типа МНК, гарантирующей минимизацию площади отклонения. Более того, если не ставить задачу интерполяции многочлена через n точек как поиск значения конкретных значений у коэффициентов многочленов — её сложность можно снизить с n^3 (вычисление через обратную матрицу) до n (вычисление через рациональный многочлен с бариоцентрическими координатами).
    
    0xd34df00d
    01.12.2022 21:58
    #24970006
    +1
    Ничё не понял.
    
    Что такое площадь отклонения? Я только MSE знаю, и оно выводится из соображений максимизации правдоподобия для одинаково распределённых (и ЕМНИП независимых) гауссовых ошибок зависимой переменной и отсутствия ошибок независимых переменных. Как только у вас зависимые ошибки начинают быть распределены по-разному, или появляются ошибки в независимых переменных, то голый МНК становится немножко неоптимальным статистически.
    
    Refridgerator
    01.12.2022 22:11
    #24970044
    Что такое площадь отклонения? Площадь — численная характеристика двумерной геометрической фигуры, которая показывает размер этой фигуры. Для функций считается через интеграл. Отклонение по площади — это разница между площадью функции и площадью аппроксимирующей функции. Чем она меньше, чем точнее аппроксимирующая функция соответствует исходной. При нуле соответственно имеем полное соответствие функции и её разложению в степенной ряд.
    
    0xd34df00d
    01.12.2022 22:14
    #24970054
    +1
    А, интеграл… То есть, вам прям на самом деле дана эта функция?
    
    Ну, считать аппроксиматор через MSE в таком случае — это что-то очень странное, ну да ладно.
    
    Refridgerator
    02.12.2022 06:39
    #24970566
    Есть много специальных функций, считать которые из определения не только затратно, но и численно неустойчиво. Гаммы, беты, эллиптические интегралы и всё такое. Как оптимизировать аппроксимант выбора особо нет — либо МНК, либо минимизация максимального отклонения, что в разы мучительнее и через умножение матриц не решается.
    
    0xd34df00d
    02.12.2022 18:30
    #24973082
    +2
    Научите решать МНК для нелинейного случая через фиксированное количество умножений матриц? А то я знаю аналитическое решение только для линейного случая, а иначе приходится делать всякие там спуски, Левенберги-Марквардты, вот это всё, и я не уверен, что это приятнее, чем считать из первых принципов.
    
    Refridgerator
    03.12.2022 12:29
    #24974664
    Это вопрос не ко мне, я в матрицах не силён. Обхожусь без них пока, гиперкомплексные числа все необходимые задачи покрывают.
    
    Refridgerator
    01.12.2022 16:00
    #24968800
    -1
    Не надоедает все мои комментарии подряд минусить? Для этого много ума не надо, равно как и для цитирования определений из википедии. Убедительнее будет решить проблемы, с которыми я сам справиться не смог, ну или показать Ваши решения, для которых не нашлось ответа в интернетах.
    
    mayorovp
    01.12.2022 15:22
    #24968618
    Как функция, не определённая в нуле, может не иметь в нём разрыва?
    
    Обычный устранимый разрыв первого рода.

DmitryKoterov
01.12.2022 06:06
#24967198
+19
Ну ваще офигеть, насколько аккуратно все математические значки и типографика в статье! Там и A одного стиля, и A другого стиля, с подвыподвертом. И ни одной орфографической ошибки не видно. Большущий респект. Видно, что человек сидел и полировал отображение, наслаждаясь процессом, как скульптор наслаждается вырезанием чего-то из дерева или камня. В наш век повального тяп-ляпства это как глоток свежего воздуха. Вот чем занимались математики 400 лет до того, как изобрели программировали (и до того, как додумались, что это можно не только читать, но и ЗАПУСКАТЬ) - полировали математические обозначения и язык.
1. Rhombus
  01.12.2022 14:43
  #24968504
  +2
  Вот чем занимались математики 400 лет до того, как изобрели
  программировали (и до того, как додумались, что это можно не только
  читать, но и ЗАПУСКАТЬ) - полировали математические обозначения и язык.
  
  Вообще-то 99% всей математики, которая нужна в физике, программировании, да и вообще почти везде, изобрели (или открыли, кому как больше нравится) задолго до программирования. Так что нет, не только обозначения и язык.
  1. AlexArt84
    01.12.2022 15:28
    #24968640
    Причем не математики открыли, а физики и инженеры. ????
    
    Rhombus
    01.12.2022 15:34
    #24968678
    +3
    Ну как, какой-нибудь Эйлер или Гаусс вполне себе математики. Но грань была не такая четкая, как сейчас, это да.
    
    Javian
    01.12.2022 18:56
    #24969492
    Собственно еще лет 40 назад были физико-математические факультеты. Физики были теми же математиками с некоторыми особенностями.
  1. 0xd34df00d
    01.12.2022 18:59
    #24969508
    +3
    Если вы говорите именно о 99% математики, нужной в программировании, а не о математике, нужной в 99% программирования, то её открыли где-то во время или позже появления программирования.

VPryadchenko
01.12.2022 10:07
#24967598
Это не по теме: мой старенький honor 10 lite спотыкается каждый раз на второй гифке (кажется, про умножение векторов). Что Вы туда запихнули?)

bear11
01.12.2022 11:44
#24967892
+3
Для полноты информации приведу ссылку на недавнюю новость о достижениях AI в умножении матриц: AI уменьшило число операций при перемножении матриц 4x4 с 49 до 47 действий:

https://science.slashdot.org/story/22/10/05/2049228/deepminds-game-playing-ai-has-beaten-a-50-year-old-record-in-computer-science

Вообще задача о том как именно и в каком порядке производить действия при перемножении матриц - интересна и нетривиальна.
1. mpa4b
  01.12.2022 17:15
  #24969120
  Про это аж в Nature написали, кстати. https://www.nature.com/articles/s41586-022-05172-4

rukhi7
01.12.2022 11:50
#24967914
+1
Больше всего понравился самый первый мультфильм, только слишком большая скорость воспроизведения там - не успеваешь рассмотреть-проверить!

Остальные мультфильмы тоже прикольные! Неплохо было бы иметь статью о том как такие мультфильмы программируются. Или они рисуются, или как этот процесс называется???

Я думаю очень популярная статья бы получилась!
1. Ktator
  01.12.2022 16:04
  #24968812
  Вот туториал от авторов библиотеки, про помощи которой делались эти мультики: https://docs.manim.community/en/stable/tutorials/index.html