26.09.2022 18:50
Monotirg 65 19000 Источник

В книге «Пятьдесят занимательных вероятностных задач с решениями - Ф. Мостеллер» есть интересная задача под номером 35.

В книге приводится решение этой задачи (что ясно из названия). В этой статье будет разобран другой подход к решению аналогичной задачи.

Первые шаги

Будем решать следующую задачу

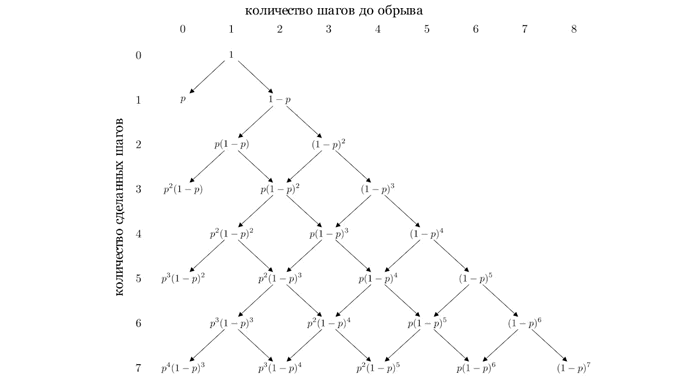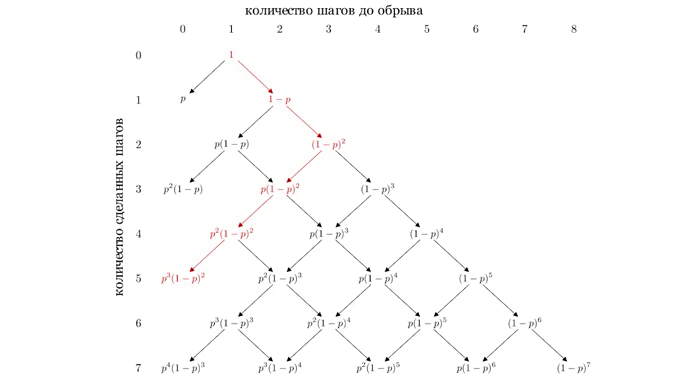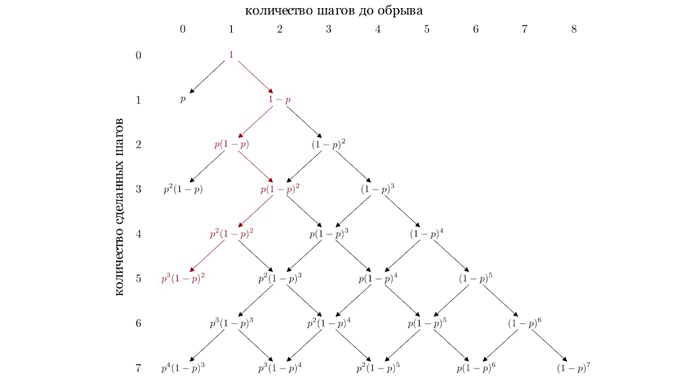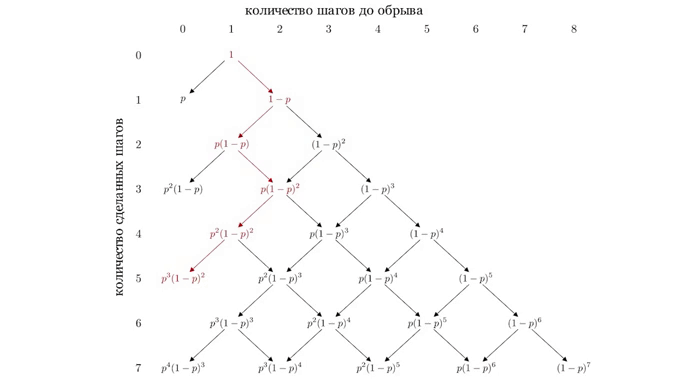
Прежде, чем переходить к решению задачи, рассмотрим, что может случится на первых шагах (рис. 1).

Рис. 1 Схема блуждания пьяницы за 7 шагов
Рис. 1 Схема блуждания пьяницы за 7 шагов

Например, вероятность того, что пьяница упадет ровно за три шага равнаp^2(1-p).Вероятность же упасть ровно за четыре шага равна0.Вообще говоря, пьяница не может упасть ровно за четное количество шагов, это можно объяснить следующим образом. Чтобы пьяница упал с обрыва, он должен находиться в начальном положение (на расстоянии одного шага от обрыва) и сделать шаг к обрыву. Пьяница находится в начальном положение только за четное количество шагов. Значит, он не может упасть за четное количество шагов.

Обозначим теперь заP_1вероятность того, что пьяница упал с обрыва, находясь при этом на расстоянии одного шага от него. Тогда,P_1можно представить в виде

P_1 = p_1 + p_3 + p_5 + \ldots = \sum_{n=0}^{\infty}p_{2n+1},

гдеp_{2n+1}вероятность того, что пьяница упадет ровно за2n+1шагов.

Получаем, что для решения задачи нужно ответить на два вопроса

  1. Какая явная формула уp_{2n+1}(очевидно, чтоp_{2n+1}зависит отp).

  2. Чему равна сумма ряда \sum_{i=0}^{\infty}p_{2n+1}.

Ответим сначала на первый вопрос.

Как в задаче про пьяницу возникают числа Каталана

Смотря на схему блуждания пьяницы (рис. 1), очевидно предположить, что

p_{2n+1} = p^{n+1}(1-p)^n,

но это не так и вот почему.

Вычислим p_5,то есть вероятность того, что пьяница упадет ровно за пять шагов. Он может упасть пройдя по одному из следующих путей:

1 \rightarrow 2 \rightarrow 3 \rightarrow 2 \rightarrow 1 \rightarrow 0, \\ 1 \rightarrow 2 \rightarrow 1 \rightarrow 2 \rightarrow 1\rightarrow 0.

Пьяница проходит по одному из путей с вероятностьюp^3(1-p)^2,кроме того, события пройти по первому пути и пройти по второму пути несовместны. Тогда, вероятность того, что пьяница упадет с обрыва ровно за пять шагов равна

p_5 = 2p^3(1-p)^2.

Можно вычислить и следующие вероятности

p_7 = 5p^4(1-p)^3, \quad p_9 = 14p^5(1-p)^4, \quad p_{11} = 42p^6(1-p)^5.

Получаем, чтоp_{2n+1}имеет вид

p_{2n+1} = c_np^{n+1}(1-p)^n,

где коэффициент c_nравен количеству путей, при которых пьяница упадет с обрыва ровно за 2n+1шагов.

Более строгое доказательство этого ниже

Строгое доказательство

Утверждение. Для любого целого неотрицательногоnверно, что

p_{2n+1} = c_np^{n+1}(1-p)^n,

где коэффициентc_nравен количеству путей, при которых пьяница упадет с обрыва ровно за2n+1шагов.

Доказательство. Доказательство проведем по индукции.

База индукции. Приn = 0утверждение верно, т.к.p_1 = p,где c_0 = 1.

Шаг индукции. Пустьp_{2n+1} = c_np^{n+1}(1-p)^n.Покажем, что из этого следует, чтоp_{2n+3} = c_{n+1}p^{n+2}(1-p)^{n+1}.

Рис. 1.1
Рис. 1.1

Поскольку,p_{2n+1} = c_np^{n+1}(1-p)^n,то вероятность того, что пьяница был в начальном положение ровно за2n+1шагов, учитывая только один путь, равна p^{n}(1-p)^n.Значит, чтобы он упал ровно за2n+3шагов, он должен сделать один шаг в сторону от обрыва и два шага в сторону обрыва (рис. 1.1).

Получаем, что пьяница упадет с обрыва ровно за2n+3шагов, учитывая только один путь, с вероятностью

p^{n}(1-p)^n \cdot (1-p) \cdot p^2 = p^{n+2}(1-p)^{n+1}.

Так как суть коэффициентаc_{n+1}- количество путей, при которых пьяница упадет с обрыва ровно за2n+3шагов, получаем

p_{2n+3} = c_{n+1}p^{n+2}(1-p)^{n+1}.

Значит, утверждение верно для любого целого неотрицательногоn.

Таким образом, чтобы ответить на первый вопрос, нужно найти явную формулу для c_n. Здесь и возникают числа Каталана.

Числа Каталана

Числами Каталана называется следующая последовательность чисел

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, \ldots

Они возникают во многих комбинаторных задачах среди которых:

  • Количество правильных скобочных последовательностей длины2n.

    Правильные скобочные последовательности длины 8
    Правильные скобочные последовательности длины 8

  • Количество путей Дика (Dyck path) длины2n.

    Пути Дика длины 8
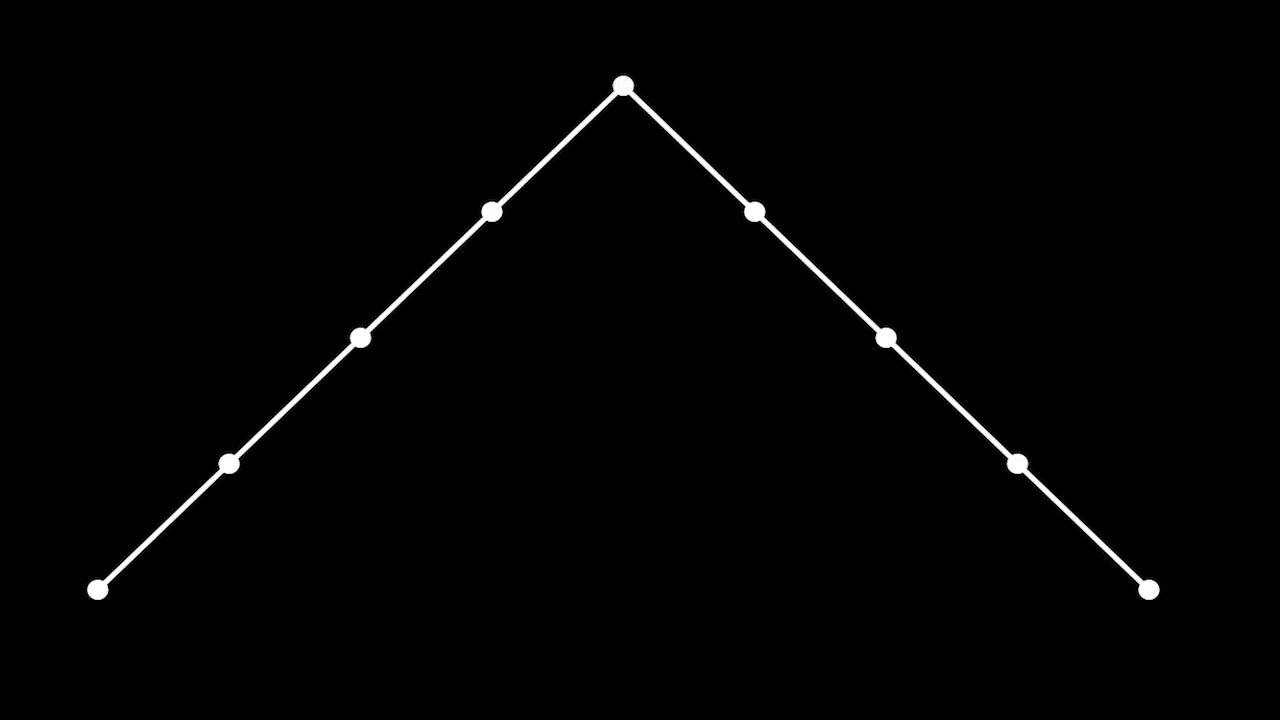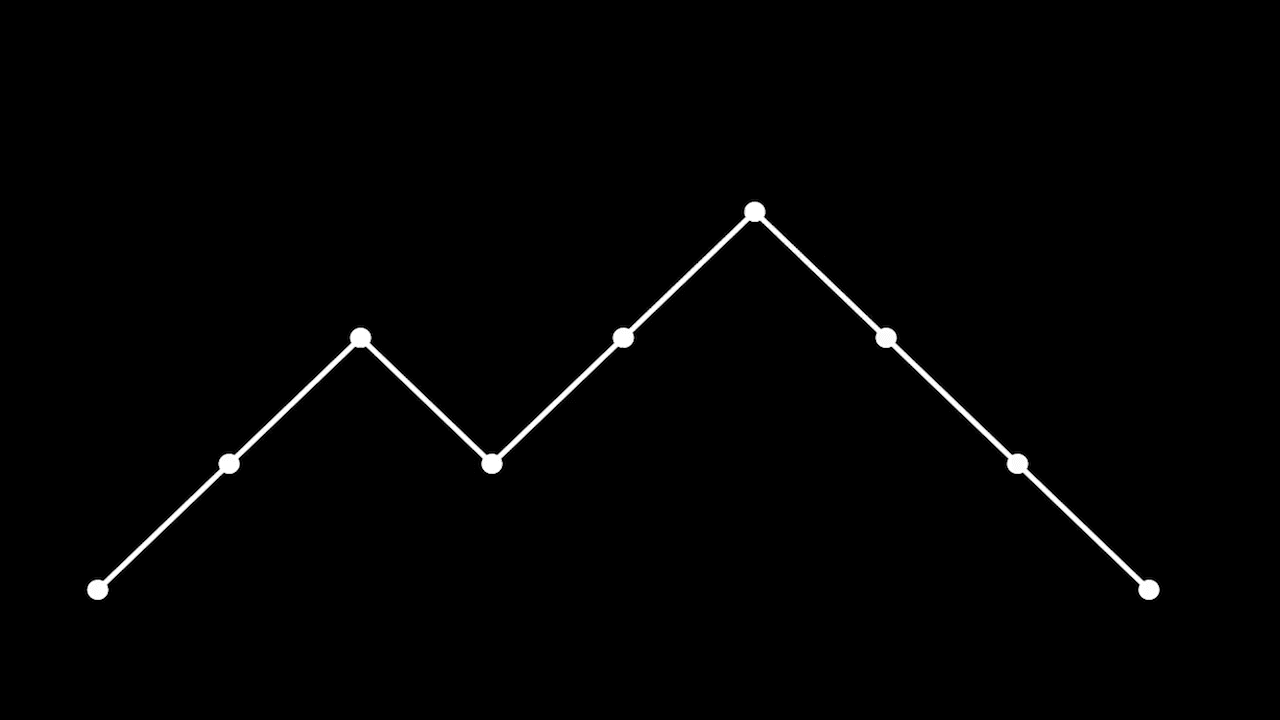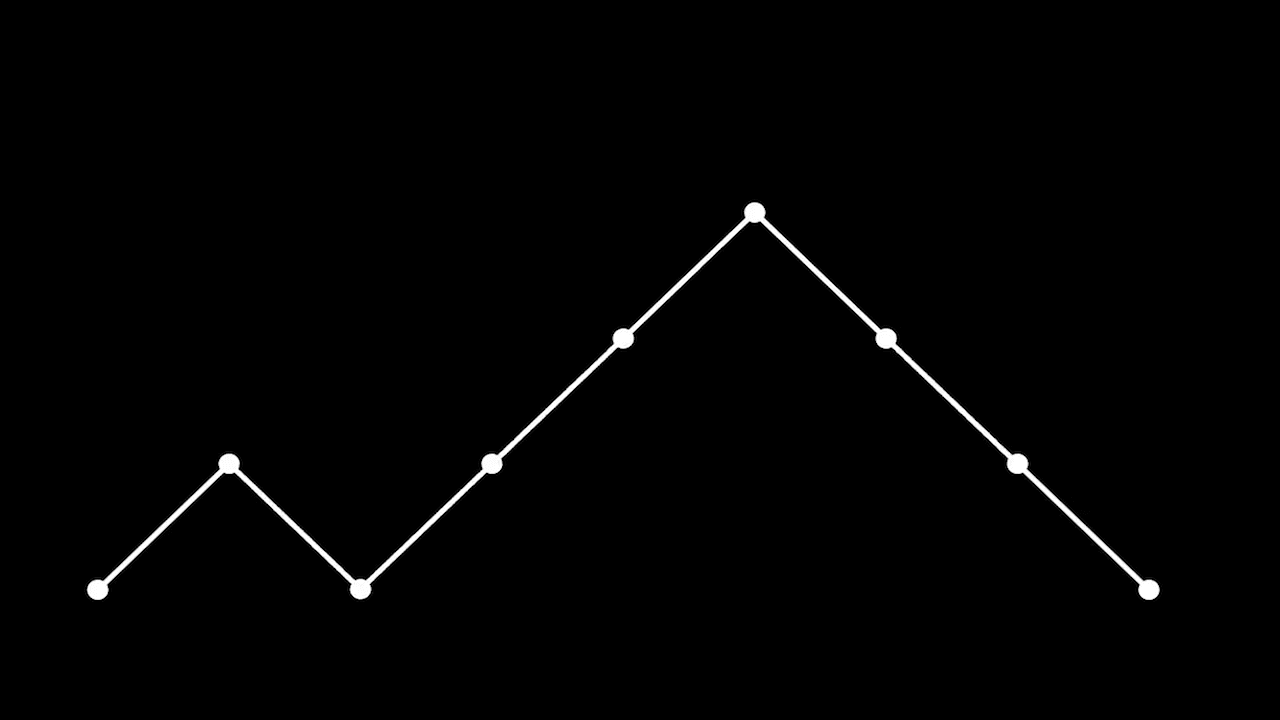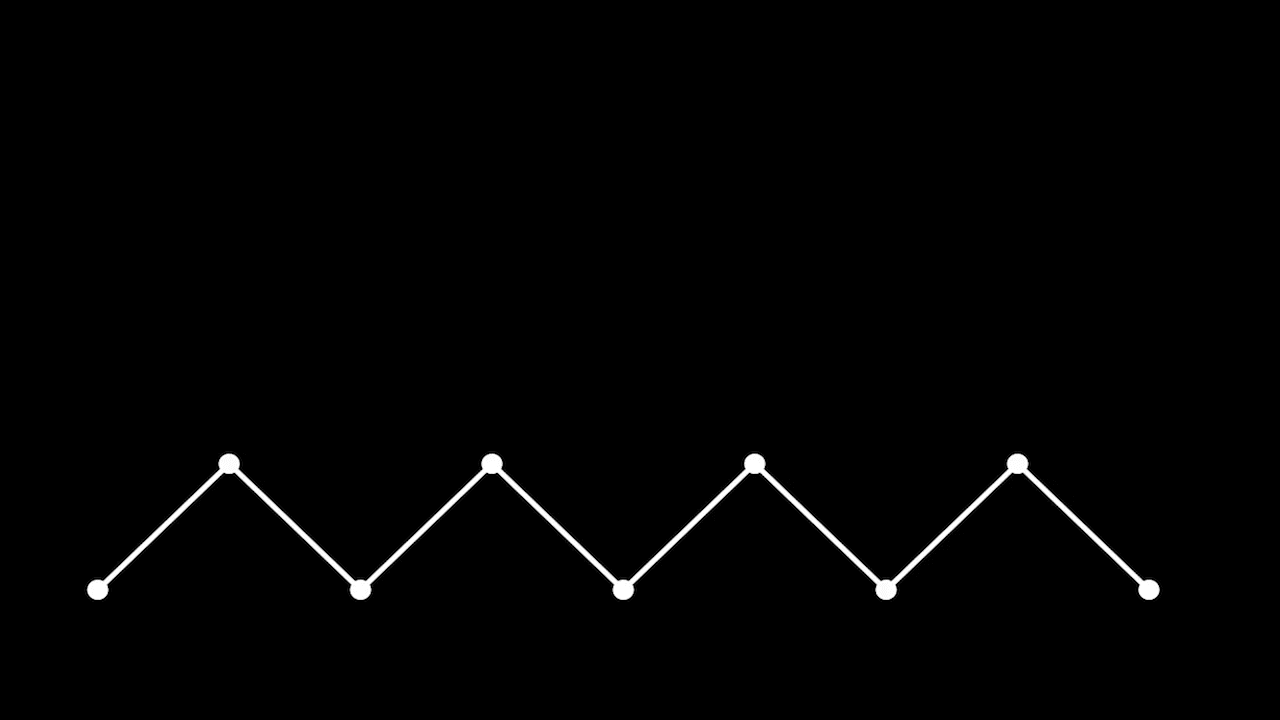
    Пути Дика длины 8

  • Количество различных триангуляций выпуклого(n+2)- угольника.

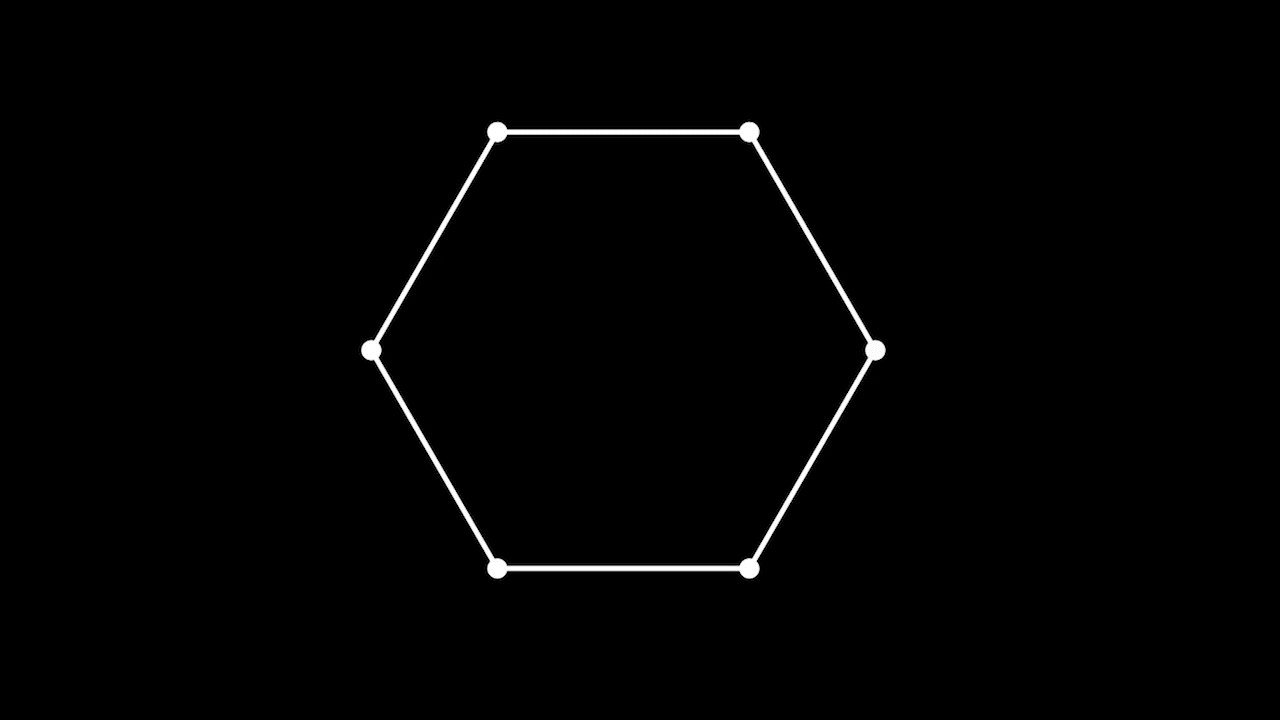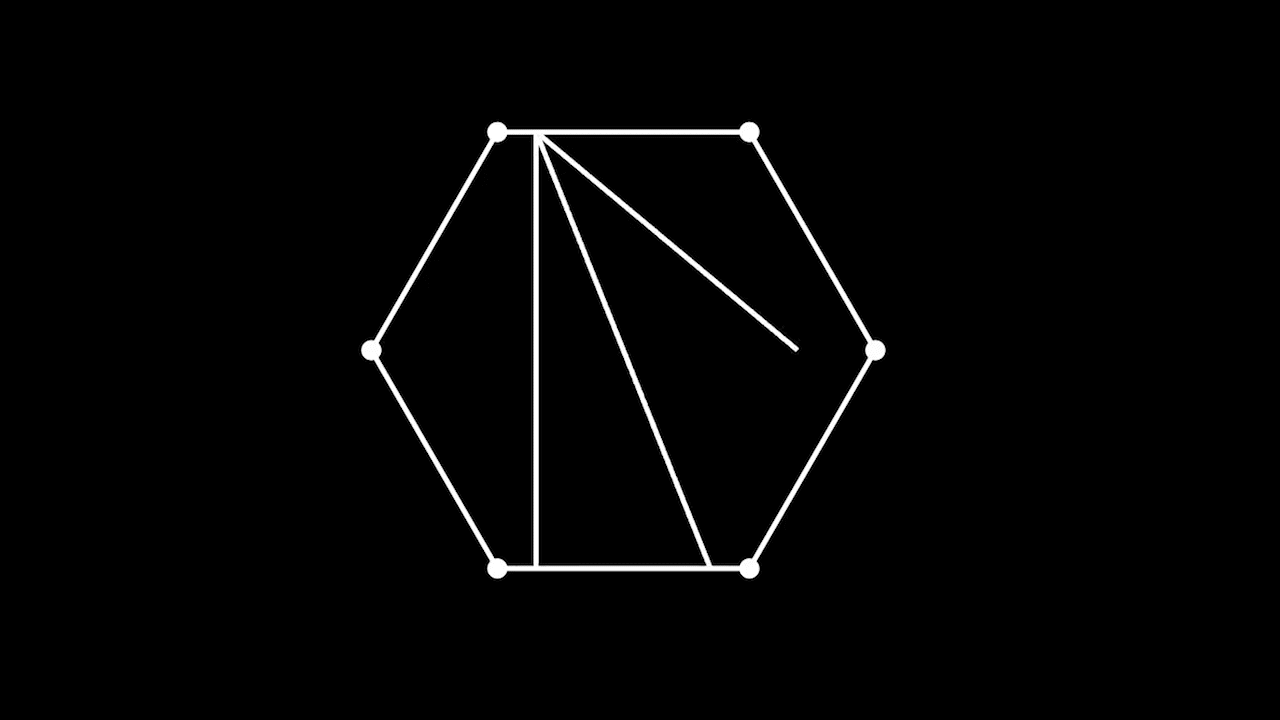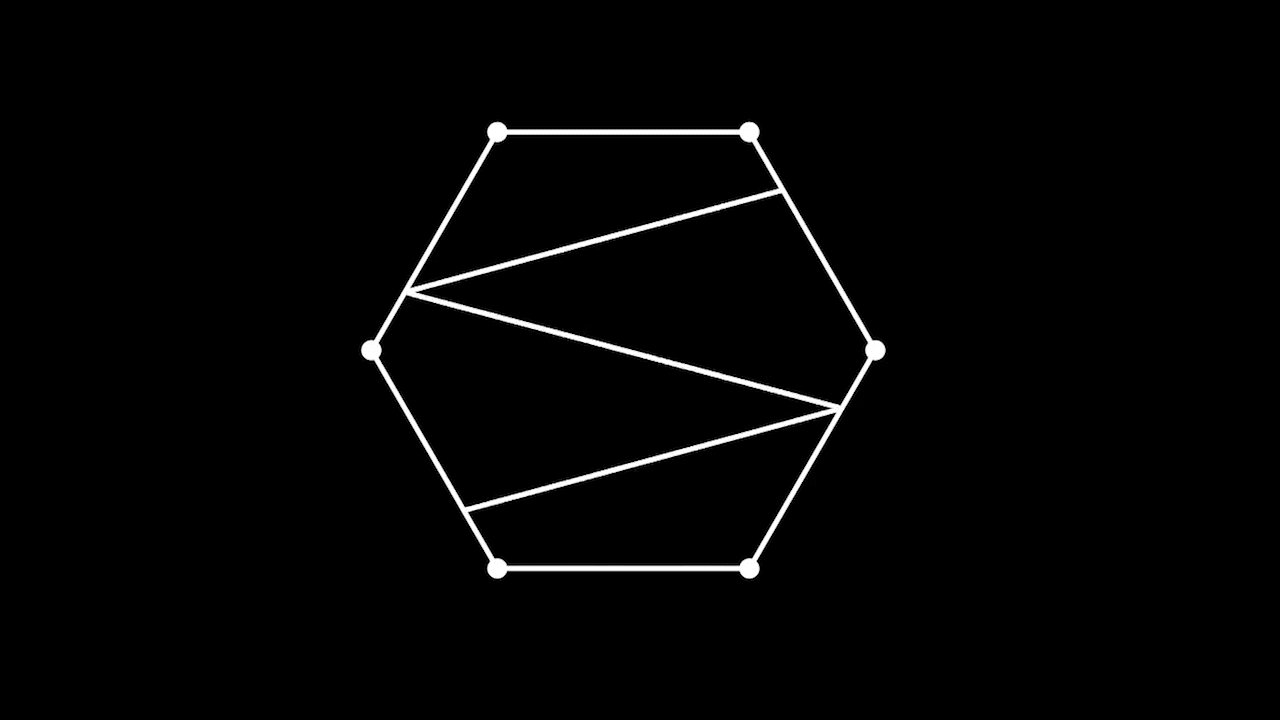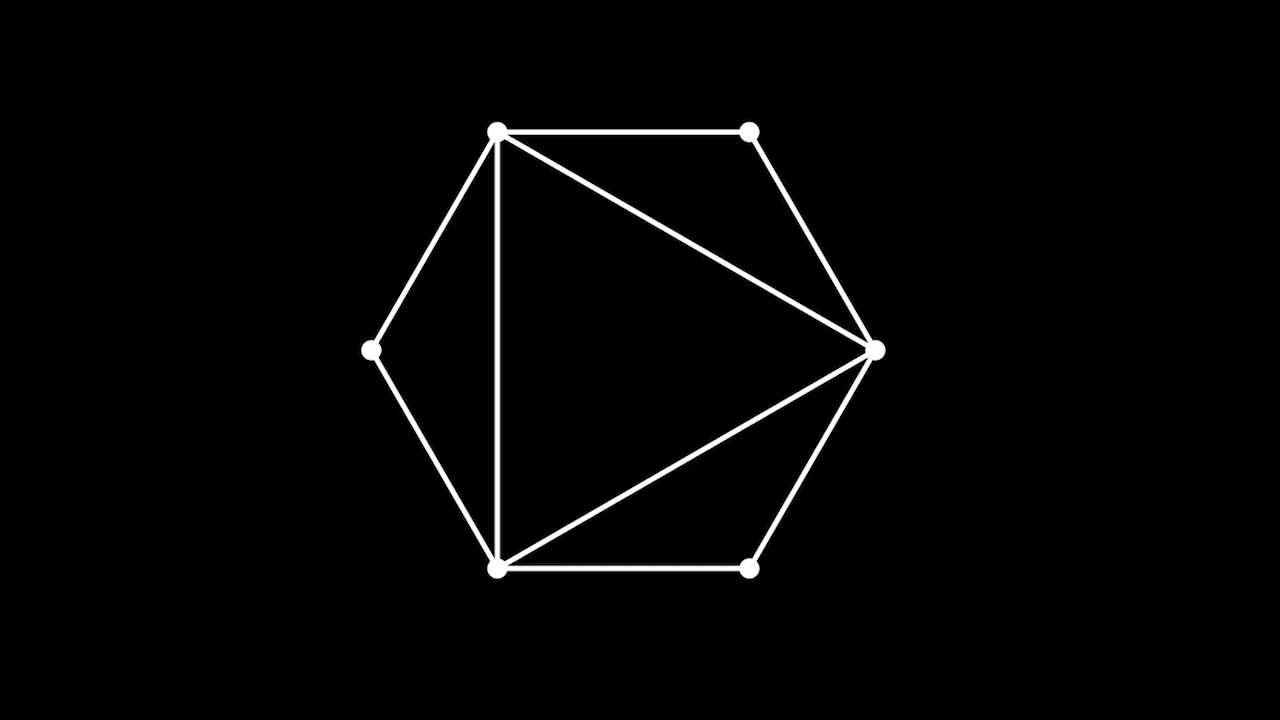
    Триангуляции правильного шестиугольника
    Триангуляции правильного шестиугольника
Первые числа Каталана, которые появляются в выше описанных задачах
Первые числа Каталана, которые появляются в выше описанных задачах

Важно отметить, что между структурами, которые появляются в этих задачах, можно установить взаимно однозначное соответствие. Так, например, каждой правильной скобочной последовательности ставится в соответствие путь Дика. Покажем это на примере нашей задачи.

Преобразуем сначала таблицу к следующему виду

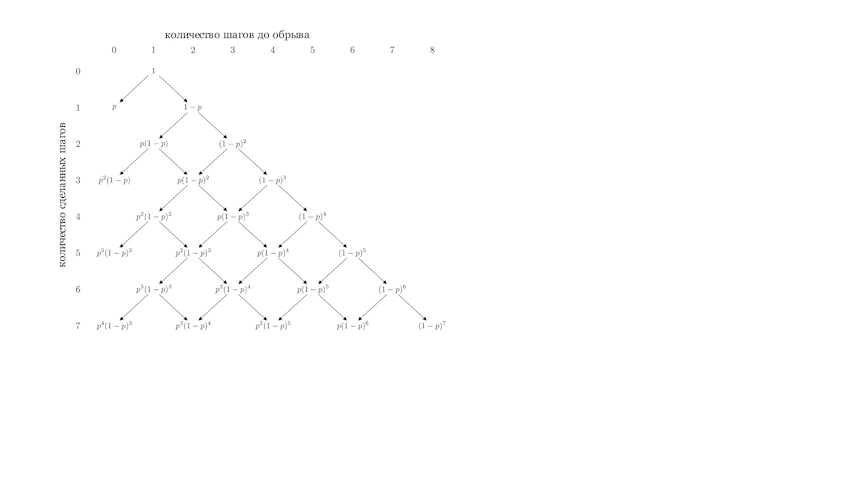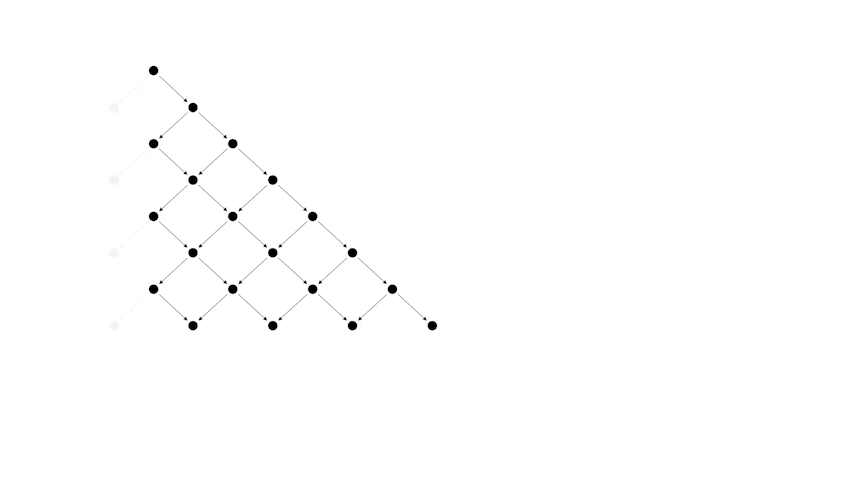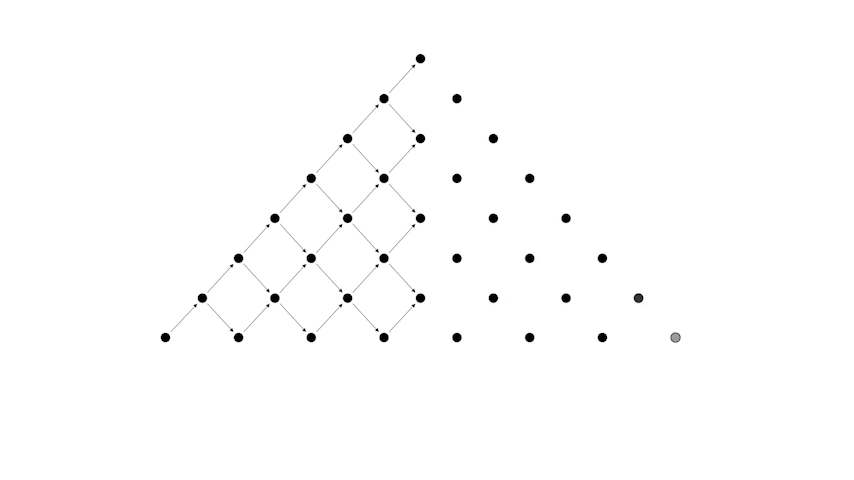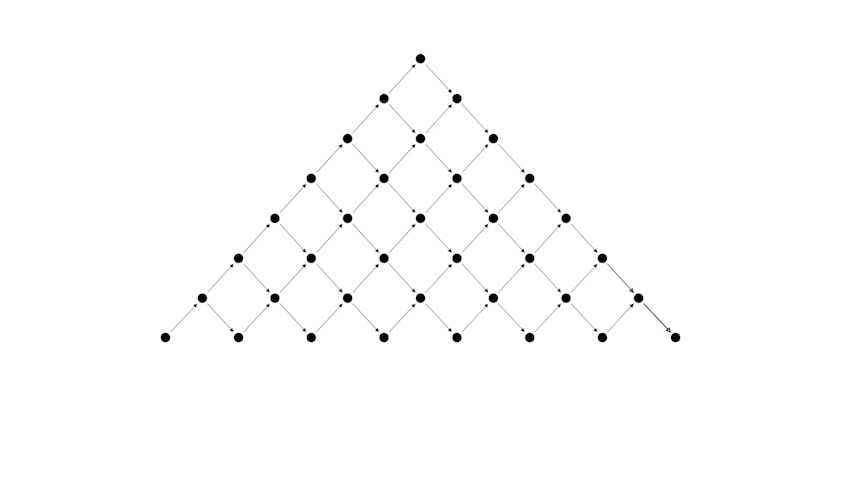
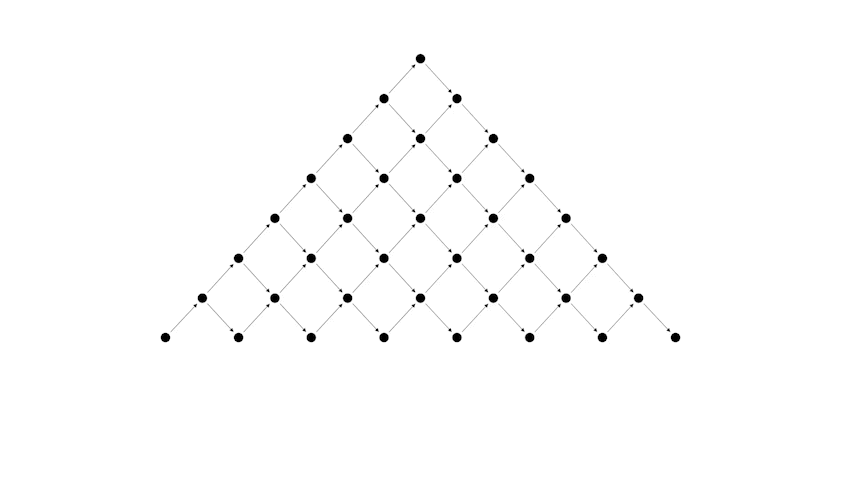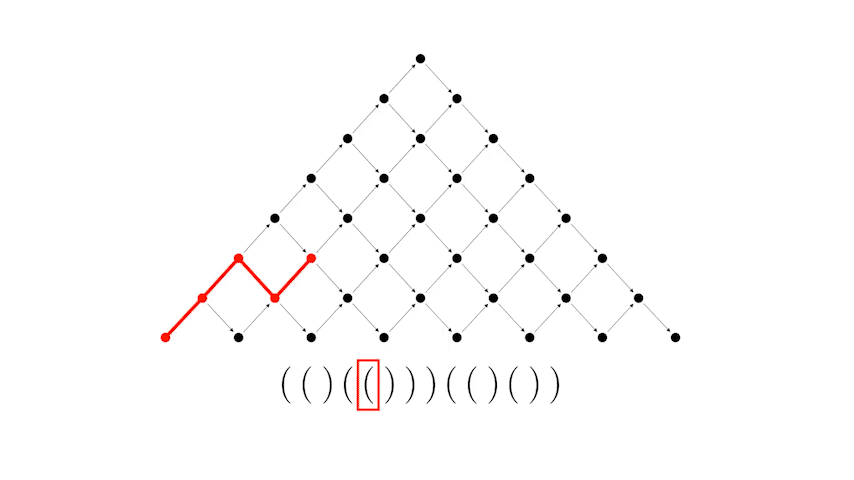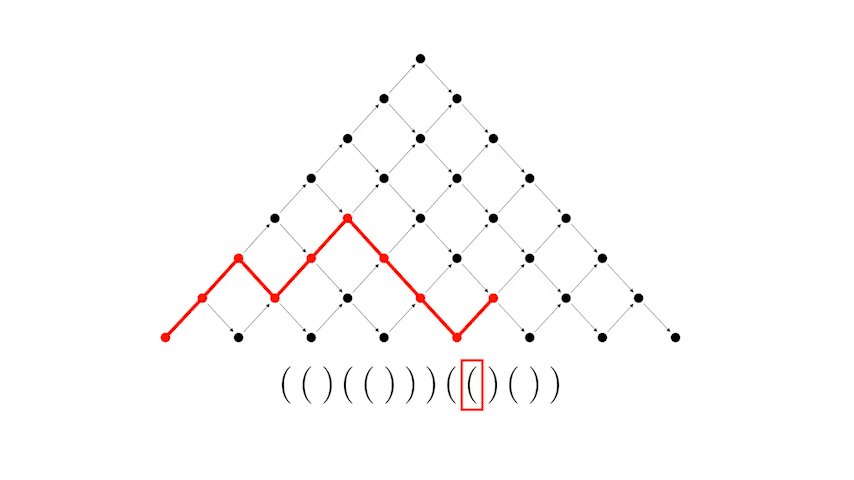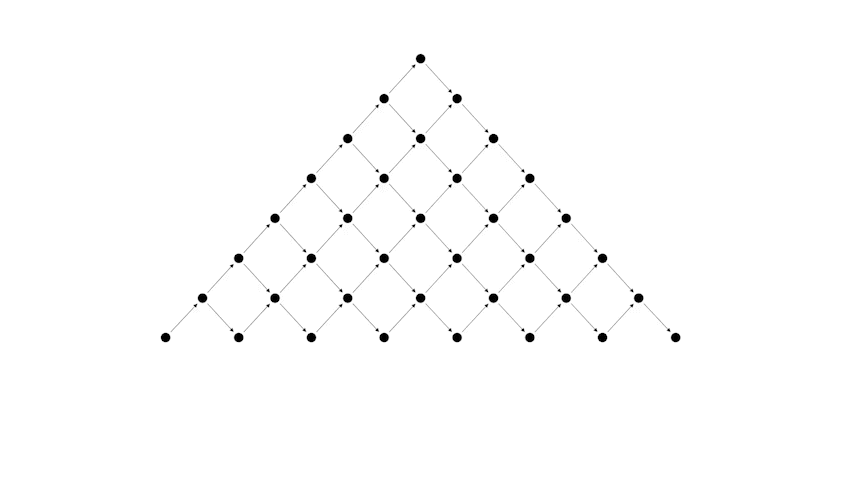
А теперь рассмотрим соответствие между правильной скобочной последовательностью и путем Дика.

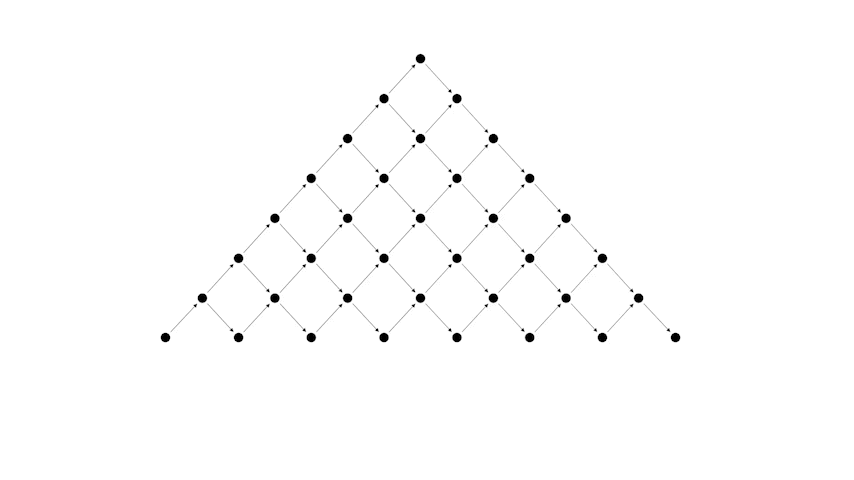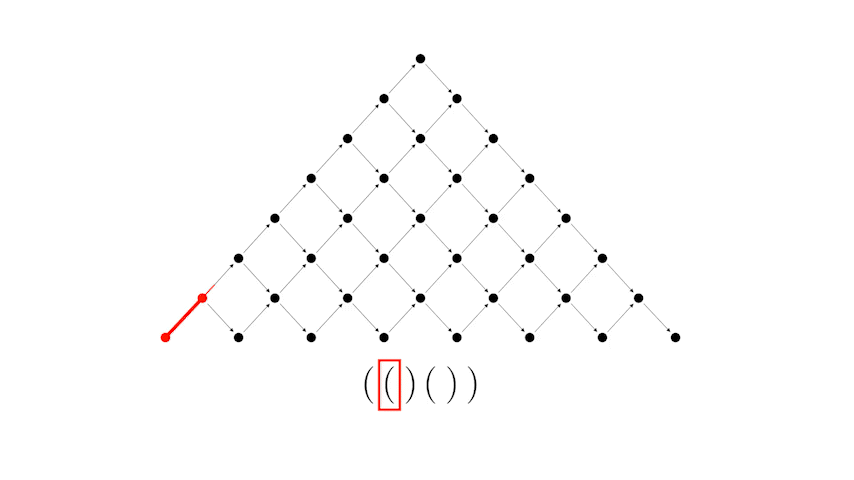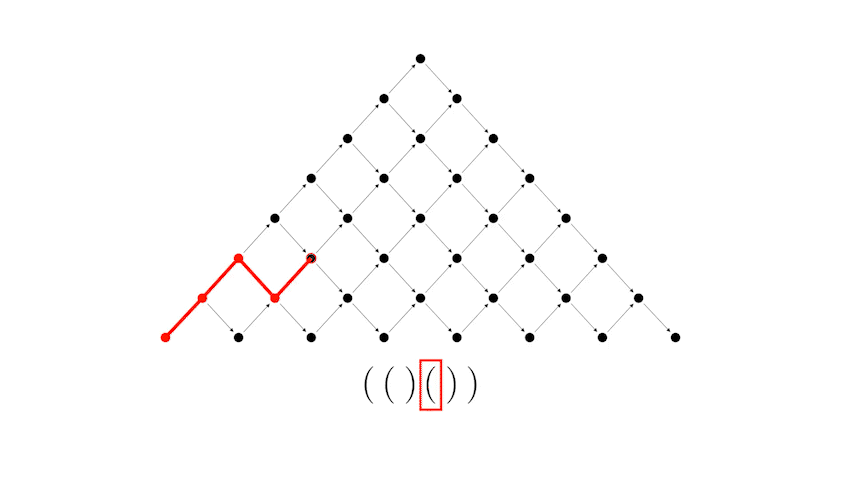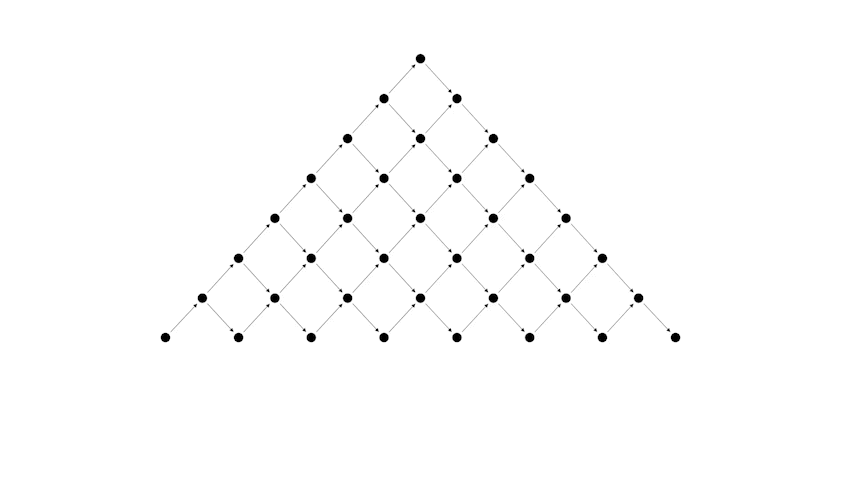
Или другой пример, более длинной скобочной последовательности

Более строгое доказательство этого ниже.

Строгое доказательство

Утверждение. Существует взаимно однозначное соответствие между множеством правильных скобочных последовательностей (п.с.п) и множеством путей Дика.

Доказательство. ПустьSиDмножества п.с.п. и путей Дика одинаковой длины соответственно.

Пустьs \in S,тогда будем писать, что

s = (i_1,i_2,\ldots,i_n),

гдеi_k = 1,если наk-ом месте стоит открывающаяся скобка, иi_k = -1,если закрывающаяся скобка.

Для элементаd \in Dвсе тоже самое, то есть

d = (i_1,i_2,\ldots,i_n),

гдеi_k = 1,еслиk-ое движение - это движение вверх, иi_k = -1,если вниз.

Осталось заметить, что для любогоs \in Sвыполнено

\sum_{t=1}^{m}i_{t} \geq 0, \quad t =1,\ldots n-1

и

\sum_{t=1}^{n}i_{t} = 0.

И тоже самое выполнено любогоd \in D.

Получаем, что множестваSиDравны. Значит, существует взаимно однозначное соответствие. Например, таковым является тождественное отображение (по сути, оно переводит открывающуюся скобку в движение вверх, а закрывающуюся в движение вниз).

Явная формула для чисел чисел Каталана

Найдем явную формулу для чисел Каталана. Для этого рассмотрим правильные скобочные последовательности длины2n.

Правильная скобочная последовательность - это

  • Пустая строка.

  • Строка вида(w), где w- правильная скобочная последовательность.

  • Строка видаw_1w_2,гдеw_1,w_2- правильные скобочные последовательности.

Первые правильные скобочные последовательности длины 2n
Первые правильные скобочные последовательности длины 2n

Рассматривая структуру правильных скобочных последовательностей, можно заметить, что все они имеют один общий вид.

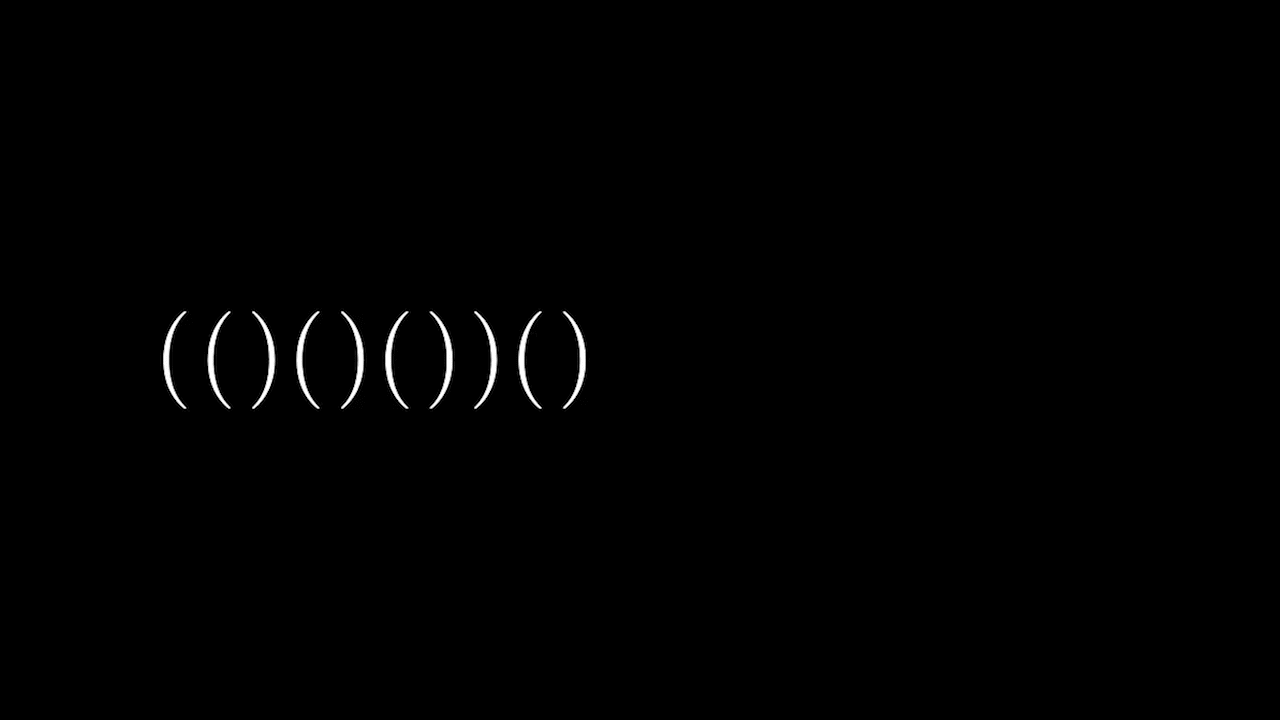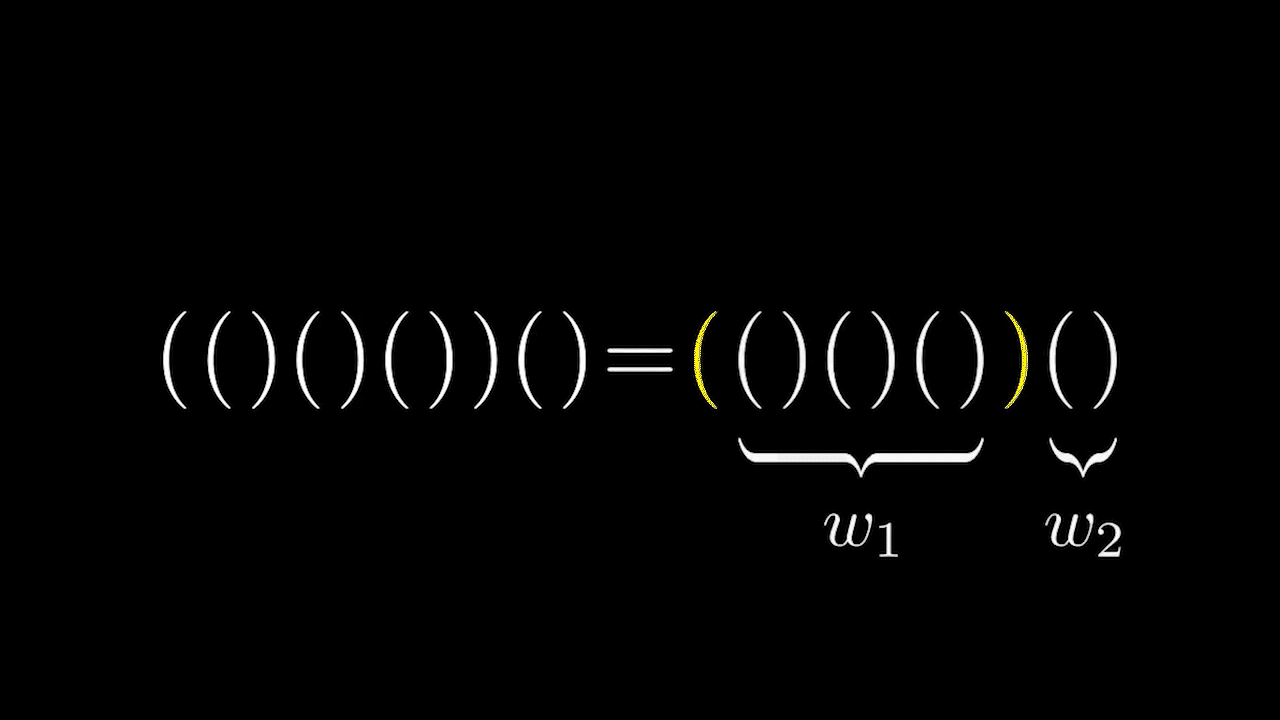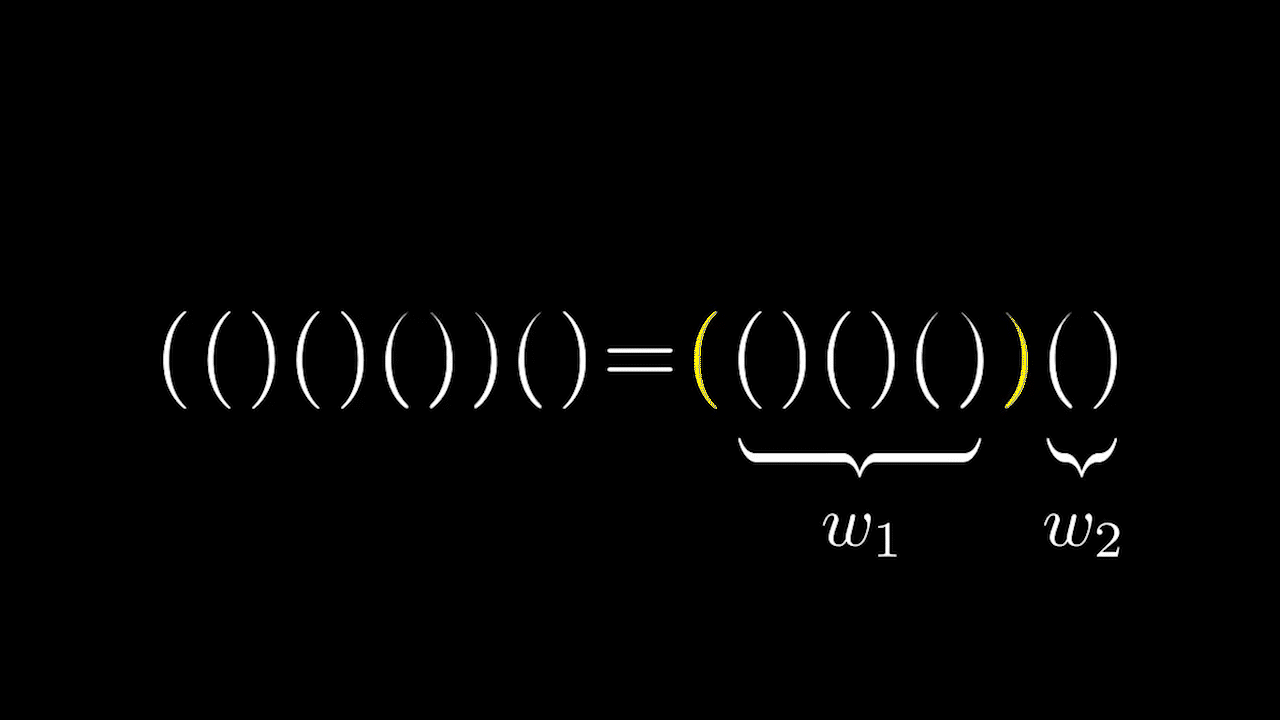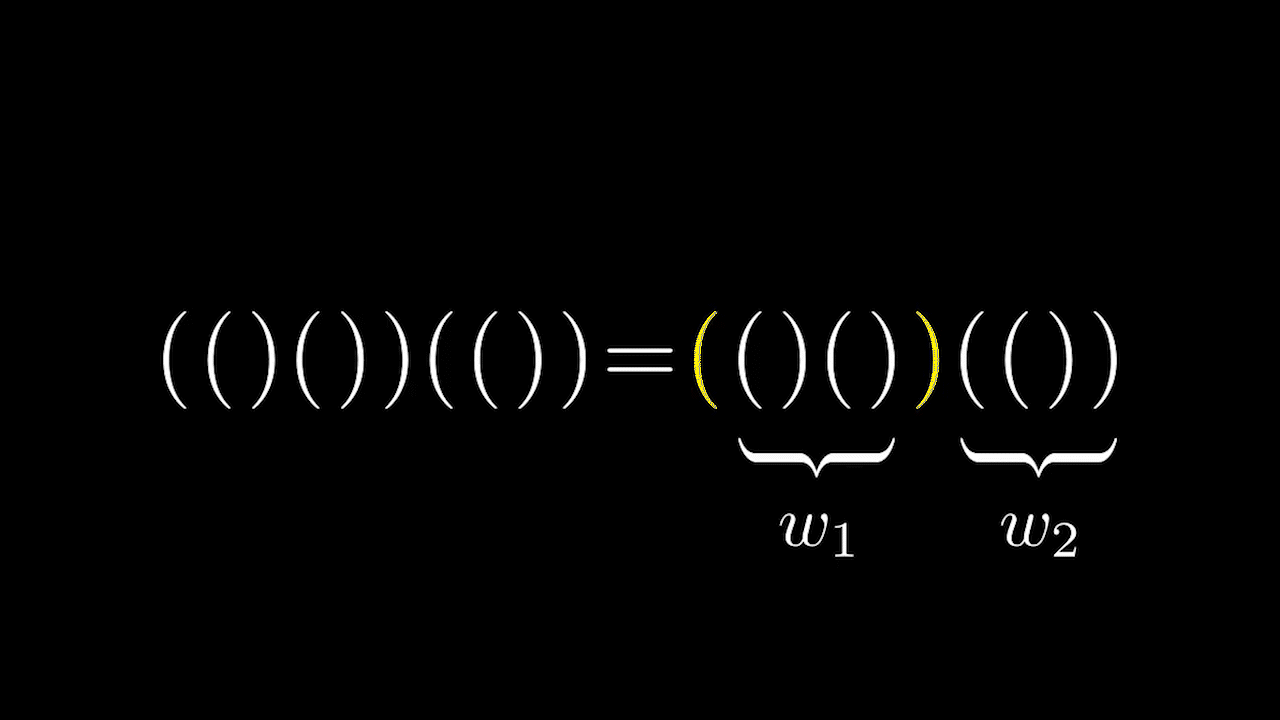
А точнее, верно следующее утверждение.

Утверждение. Каждая правильная скобочная последовательностьw(кроме пустой) имеет вид

w= (w_1)w_2,

гдеw_1,w_2- правильные скобочные последовательности.

Доказательство этого ниже.

Доказательство

Заметим, что любая правильная скобочная последовательность начинается с открывающейся скобки, иначе она не правильная скобочная последовательность. Поэтому, найдем такую закрывающуюся скобку, что

w = (w_1)w_2,

гдеw_1- правильная скобочная последовательность.

Это можно сделать следующим образом:

  1. Пустьi = 1.

  2. Рассматриваем вторую скобку.

  3. Если рассматриваемая скобка открывающаяся, то увеличиваемiна 1,иначе уменьшаем на1.

  4. Еслиi=0,то последняя рассматриваемая скобка и есть искомая, иначе рассматриваем следующую скобку и переходим к пункту 3 и 4.

Мы всегда найдем такую закрывающуюся скобку, т.к.w- правильная скобочная последовательность, а из этого следует, что количество открывающихся и закрывающихся скобок равно, то есть на последней скобкеi = 0.

Так какw_1- правильная скобочная последовательность, то и(w_1)- правильная скобочная последовательность. Из этого следует, чтоw_2- правильная скобочная последовательность, иначеw- не правильная скобочная последовательность.

Получаем, что каждая правильная скобочная последовательность (кроме пустой) имеет выше описанный вид.

Пусть теперьC_n- n-ое число Каталана или, что тоже самое, количество правильных скобочных последовательностей длины2n.Выведем из утверждения выше рекуррентное соотношение

C_n = C_{0}C_{n-1}+C_{1}C_{n-2}+\ldots+C_{n-1}C_{0} = \sum_{i=0}^{n-1}C_{i}C_{n-i-1}
Вывод рекуррентного соотношения

Пустьw- правильная скобочная последовательность длины2n.Из утверждения выше следует, что она представима в виде

w=(w_1)w_2,

гдеw_1,w_2- правильные скобочные последовательности. Поэтому, рассмотрим варианты длинw_1и w_2.

Если длинаw_1равна0,то длинаw_2равна2n-2.Тогда, количество правильных скобочных последовательностей данного вида равноC_{0}C_{n-1}, т.к. количество правильных скобочных последовательностей длины0равноC_0,а длины2n-2равноC_{n-1.}

Если длинаw_1равна2,то длинаw_2равна2n-4.Тогда, количество правильных скобочных последовательностей данного вида равноC_{1}C_{n-2.}

Продолжая по аналогии, в конце получим. Если длинаw_1равна2n-2,то длинаw_2равна0.Тогда, количество правильных скобочных последовательностей данного вида равноC_{n-1}C_{0}.

Складывая количества правильных скобочных последовательностей каждого вида, получим количество правильных скобочных последовательностей длины 2nи искомое рекуррентное соотношение.

Осталось решить это рекуррентное соотношение. Вообще говоря, решать рекуррентные соотношения можно несколькими способами, например, выделяют линейные рекуррентные соотношения и их решение аналогично способу решения линейных дифференциальных уравнений с постоянными коэффициентами. Но наше рекуррентное соотношение таковым не является, поэтому будет решать его с помощью производящей функции.

Напомню, что это такое.

Производящая функция

Простыми словами, производящая функция - это следующий ряд

a_0+a_1z+a_2z^2+\ldots=\sum_{n=0}^{\infty}a_nz^n,

где коэффициентыa_0,a_1,a_2,\ldots- члены последовательности.

Более строго, пусть дана последовательность\{a_n\},тогда формально степенной рядG(z),который имеет вид

G(z) = a_0+a_1z+a_2z^2+\ldots=\sum_{n=0}^{\infty}a_nz^n,

называется производящей функциейG(z)данной последовательности.

В определение стоит обратить внимание на то, что, вообще говоря, производящая функция - это формально степенной ряд.

В отличие от обычных степенных рядов, у формально степенных рядов зачастую не рассматривают сходимость. Как следствие этого, нет смысла подставлять вместоzкакое-либо значение, за некоторым исключением. Например, если подставить в рядz=0,то G(0) = a_0.

Так зачем они вообще нужны?

А вот зачем, для формально степенных рядов можно определить операции сложения и умножения следующим образом

A(z)+B(z) = \sum_{n=0}^{\infty}a_nz^n + \sum_{n=0}^{\infty}b_nz^n = \sum_{n=0}^{\infty}(a_n + b_n)z^n = \sum_{n=0}^{\infty}c_nz^n = C(z);A(z)B(z) = (\sum_{n=0}^{\infty}a_nz^n)(\sum_{n=0}^{\infty}b_nz^n)=\sum_{n=0}^{\infty}(\sum_{k=0}^{n}a_kb_{n-k})z^n = \sum_{n=0}^{\infty}c_nz^n = C(z).

И если коэффициенты ряда принадлежат кольцуR,то и формально степенные ряды образуют кольцо относительно этих операций, которое обозначаетсяR[[z]].Так ещё оказывается, что, если кольцоRобладало каким-либо свойством, то и кольцоR[[z]]может обладать этим свойством.

Для нас же наиболее важно то, что формально степенные ряды именно образуют кольцо. Важность этого мы увидим далее.

ПустьG(z)- производящая функция последовательности чисел Каталана, то есть

G(z) = \sum_{n=0}^{\infty}C_nz^n.

Воспользуемся рекуррентным соотношением и распишем правую часть

G(z) = \sum_{n=0}^{\infty}C_nz^n = C_0 + \sum_{n=1}^{\infty}(\sum_{k=0}^{n-1}C_{k}C_{n-k-1})z^n.

Преобразуем правую часть, двойную сумму можно представить в следующем виде

\sum_{n=1}^{\infty}(\sum_{k=0}^{n-1}C_{k}C_{n-k-1})z^n=zG^2(z).
Преобразование двойной суммы

Прежде чем переходить к преобразованию, введем определение свертки последовательностей.

Пусть даны последовательности\{a_n\}, \{b_n\} и\{c_n\}.Последовательность\{c_n\}называется сверткой последовательностей\{a_n\}и\{b_n\},если

c_n = \sum_{i=0}^{n}a_{i}b_{n-i}.

Пусть теперьA(z),B(z)иC(z)производящие функции последовательностей \{a_n\}, \{b_n\}и\{c_n\}соответственно. Тогда, из определения умножения для формально степенных рядов, следует, что

A(z)B(z) = C(z).

То есть, получаем следующее свойство. Произведение производящих функций есть производящая функция свертки последовательностей.

Рассмотрим свертку следующих последовательностей

\{C_0,C_1,C_2,\ldots\} \quad\text{и} \quad \{0,C_0,C_1,\ldots\}.

Получим последовательность

\{0,C_0C_0,C_0C_1+C_0C_1,\ldots,C_0C_{n-1}+\ldots+C_{n-1}C_0,\ldots\}.

Получаем, что множитель

\sum_{n=1}^{\infty}(\sum_{k=0}^{n-1}C_{k}C_{n-k-1})z^n

есть производящая функция свертки, а по свойству описанному выше, получаем, что этот множитель равен произведению производящих функций.

Производящая функция последовательности\{C_0,C_1,C_2,\ldots\}естьG(z).

Производящая функция последовательности\{0,C_0,C_1,\ldots\}есть

C_0z+C_1z^2+C_2z^3+\ldots=\sum_{n=0}^{\infty}C_nz^{n+1}=z\sum_{n=0}^{\infty}C_nz^{n}=zG(z).

Значит,

\sum_{n=0}^{\infty}(\sum_{k=0}^{n-1}C_{k}C_{n-k-1})z^n = zG^2(z).

И с тем учетом, чтоC_0=1,получаем

G(z)=1+zG^2(z).

Решаем квадратное уравнение относительноG(z)и находим, что

G(z) = \frac{1-\sqrt{1-4z}}{2z} \quad \text{или} \quad G(z) = \frac{1+\sqrt{1-4z}}{2z}.

Чтобы понять, какой знак выбрать, перепишем равенства в следующий вид

zG(z) = \frac{1-\sqrt{1-4z}}{2} \quad \text{или} \quad zG(z) = \frac{1+\sqrt{1-4z}}{2},

и подставимz=0,получим

0=0 \quad \text{или} \quad 0 = 1.

Слева верное равенство, значит

G(z) = \frac{1-\sqrt{1-4z}}{2z}.

Разложим теперь правую часть в ряд

\frac{1-\sqrt{1-4z}}{2z} = \sum_{i=0}^{n}\frac{1}{n+1}\binom{2n}{n}z^n.
Разложение правой части в ряд

Воспользуемся тем, что

(1+x)^\alpha = 1 + \sum_{n=1}^{\infty}\binom{\alpha}{n}x^n.

Тогда,

\sqrt{1-4z} = 1 + \sum_{n=1}^{\infty}\binom{\frac{1}{2}}{n}(-4z)^n.

Осталось подставить и преобразовать

\frac{1-\sqrt{1-4z}}{2z} = -\sum_{n=1}^{\infty}\binom{\frac{1}{2}}{n}\frac{(-4z)^n}{2z} = \sum_{n=0}^{\infty}(-1)^{n}\binom{\frac{1}{2}}{n+1} \cdot 2\cdot4^nz^{n}.

Преобразуем множитель\binom{\frac{1}{2}}{n+1}отдельно

\binom{\frac{1}{2}}{n+1} = \frac{\prod\limits_{k=0}^{n}(\frac{1}{2}-k)}{(n+1)!}= \frac{\prod\limits_{k=0}^{n}(1-2k)}{2^{n+1}(n+1)!}=\frac{(-1)^{n+1}\prod\limits_{k=0}^{n}(2k-1)}{2^{n+1}(n+1)!} == \frac{(-1)^{n}\prod\limits_{k=0}^{n-1}(2k+1)}{2^{n+1}(n+1)!}= \frac{(-1)^{n}\prod\limits_{k=0}^{n-1}(2k+1) \prod\limits_{k=1}^{n}(2k)}{2^{n+1} \prod\limits_{k=1}^{n}(2k)(n+1)!} = \frac{(-1)^{n}(2n)!}{2^{2n+1}\prod\limits_{k=1}^{n}k \, (n+1)!}== (-1)^n \cdot\frac{1}{2^{2n+1}} \cdot \frac{(2n)!}{n!(n+1)!} = (-1)^n \frac{1}{2^{2n+1}(n+1)}\binom{2n}{n}.

Подставляем и после сокращения, получаем

\frac{1-\sqrt{1-4z}}{2z}= \sum_{n=0}^{\infty} \frac{1}{n+1} \binom{2n}{n} z^n.

То есть

G(z)=\sum_{i=0}^{\infty}C_nz^n= \sum_{i=0}^{n}\frac{1}{n+1}\binom{2n}{n}z^n.

Получаем, что ряды равны, значит и коэффициенты перед одинаковыми степенями равны, то есть

C_n = \frac{1}{n+1}\binom{2n}{n}z^n.

Мы нашли явную формулу для чисел Каталана.

Маленькое замечание для тех, кому интересна мат. часть

А законно ли то, что мы сделали?

Например, когда выбирали знак дляG(z)или использовали ряд Тейлора для формально степенного ряда.

Правильно ли всё это?

Скучный ответ заключается в том, чтобы ответить. Вот, мы получили формулу для чисел Каталан, осталось её доказать с помощью мат. индукции. И да, это в каком-то смысле правильный ответ. Но нужно ли всё это? В данном случае, нет.

Важно понимать, что мы работаем в кольце формально степенных рядов, то есть мы должны понимать, что выражение

\frac{1-\sqrt{1-4z}}{2z}

является формально степенным рядом. Структура кольца позволяет нам складывать, вычитать, умножать и в некоторых случаях делить. Как в целых числах, некоторые числа делятся, некоторые нет. Этим, кстати, можно было воспользоваться, когда мы выбирали знак.

Если бы мы выбрали знак плюс, то в числители получился бы ряд, который не делится на2z(2zтакже является формальным рядом).

А что значит, что один ряд делится на другой ряд?

Поделить один ряд на другой, например, рядA(z) на рядB(z), это значит решить следующее уравнение относительноC(z)

A(z)=B(z)\cdot C(z).

Если расписать равенство через коэффициенты рядов, то получится бесконечная система. Иногда она будет иметь решение, иногда нет. Это зависит от того, будет лиB(z)обратим. Достаточным и необходимым условием этого является обратимость его свободного члена (что легко доказывается).

Или эта формула

(1+x)^\alpha = 1 + \sum_{n=1}^{\infty}\binom{\alpha}{n}x^n.

Она остается верной и для формально степенных рядов, единственное, чтобы воспользоваться ей, нужно рассматривать формальные ряды над полем, вместо кольца.

Кроме того, что значит извлечь корень из какого-либо ряда, например, извлечь корень из рядаA(z).По сути, нужно решить следующее уравнение относительно B(z)

A(z) = B(z)\cdot B(z).

Если опять таки расписать равенство через коэффициенты рядов, то получится бесконечная система. И она опять таки иногда будет иметь решение, иногда нет.

Обратно к задаче про пьяницу

Вот мы и нашли явную формулу дляc_n,тем самым и явную формулу дляp_{2n+1}.Теперь дело за малым, подставить в сумму всё, что мы нашли, и найти эту сумму.

Имеем

P_1 = \sum_{n=0}^{\infty}p_{2n+1} = p\sum_{i=0}^{\infty}C_n(p(1-p))^n.

Найдем эту сумму с помощью производящей функции, которую нашли ранее. Мы знаем, что

\sum_{i=0}^{\infty}C_nz^n = \frac{1-\sqrt{1-4z}}{2z}, \quad\forall z\in\mathbb{R}: |z|\leq\frac{1}{4}.

Подставимz = p(1-p),получим

\sum_{i=0}^{\infty}C_n(p(1-p))^n = \frac{1-\sqrt{1-4p(1-p)}}{2p(1-p)}, \quad \forall p \in \mathbb{R}:p\in[0,1].

И наша сумма легко находится

P_1 = p\sum_{i=0}^{\infty}C_n(p(1-p))^n= \frac{1-\sqrt{1-4p(1-p)}}{2(1-p)}, \quad \forall p \in \mathbb{R}:p\in[0,1].
Второе маленькое пояснение для тех, кому интересна мат. часть

Было оговорено, что производящая функция - это формальный степенной ряд, а теперь мы подставляем значения вместоzи находим сумму.

Правильно ли это?

Зададимся таким вопросом, а что нам мешает вместо формально степенного ряда использовать обычный степенной ряд? А вот что, мы не можем выполнять никакие действия с рядом, пока ничего не знаем про его сходимость. Другими словами, для этого перехода мы должны исследовать сходимость этого ряда, что будет сделано ниже.

Исследование сходимости ряда

Найдем сперва радиус сходимости

\lim\limits_{n \rightarrow \infty} \frac{|C_{n+1}z^{n+1}|}{|C_nz^n|} = |z|\lim\limits_{n \rightarrow \infty} \frac{(n+1)\binom{2n+2}{n+1}}{(n+2)\binom{2n}{n}} = |z|\lim\limits_{n \rightarrow \infty} \frac{(2n+2)! n! n!}{(2n)! (n+1)! (n+1)!} ==|z|\lim\limits_{n \rightarrow \infty} \frac{(2n+1)(2n+2)}{(n+1)^2} = 4 |z| < 1 \Rightarrow |z| < \frac{1}{4}.

Теперь рассмотрим сходимость ряда приz = \frac{1}{4}

G(\frac{1}{4}) = \sum\limits_{n=0}^{\infty}\frac{C_n}{4^n}=\sum\limits_{n=0}^{\infty}\frac{1}{4^n(n+1)}\binom{2n}{n}.

Воспользуемся тем, что

\binom{2n}{n} \sim \frac{4^n}{\sqrt{\pi n}}.

Это можно вывести из формулы Стерлинга

n! \sim \sqrt{2\pi n} \left({n \over e}\right)^n.

Получаем

\frac{1}{4^n(n+1)}\binom{2n}{n} \sim \frac{1}{(n+1)\sqrt{\pi n}},

то есть ряд

\sum_{n=0}^{\infty}\frac{1}{(n+1)\sqrt{\pi n}},

который сходится. Значит и исходный ряд сходится приz = \frac{1}{4}.Кроме того, ряд сходится и приz=-\frac{1}{4}(абсолютная сходимость).

Таким образом, исходный ряд сходится при|z| \leq \frac{1}{4}.

Подставим теперьz=p(1-p),гдеp\in[0,1],получим ряд

\sum_{i=0}^{\infty}C_n(p(1-p))^n = \frac{1-\sqrt{1-4p(1-p)}}{2p(1-p)},

который сходится для любогоp\in[0,1],так как

|p(1-p)|\leq \frac{1}{4} \Leftrightarrow (p-\frac{1}{2})^2\geq0.

То есть все действия, который мы выполняли с исходным рядом, имеют смысл.

Это и есть ответ на нашу задачу. Пьяница упадет с обрыва, находясь при это на расстоянии одного шага от него, с вероятностью

P_1 = \frac{1-\sqrt{1-4p(1-p)}}{2(1-p)}.

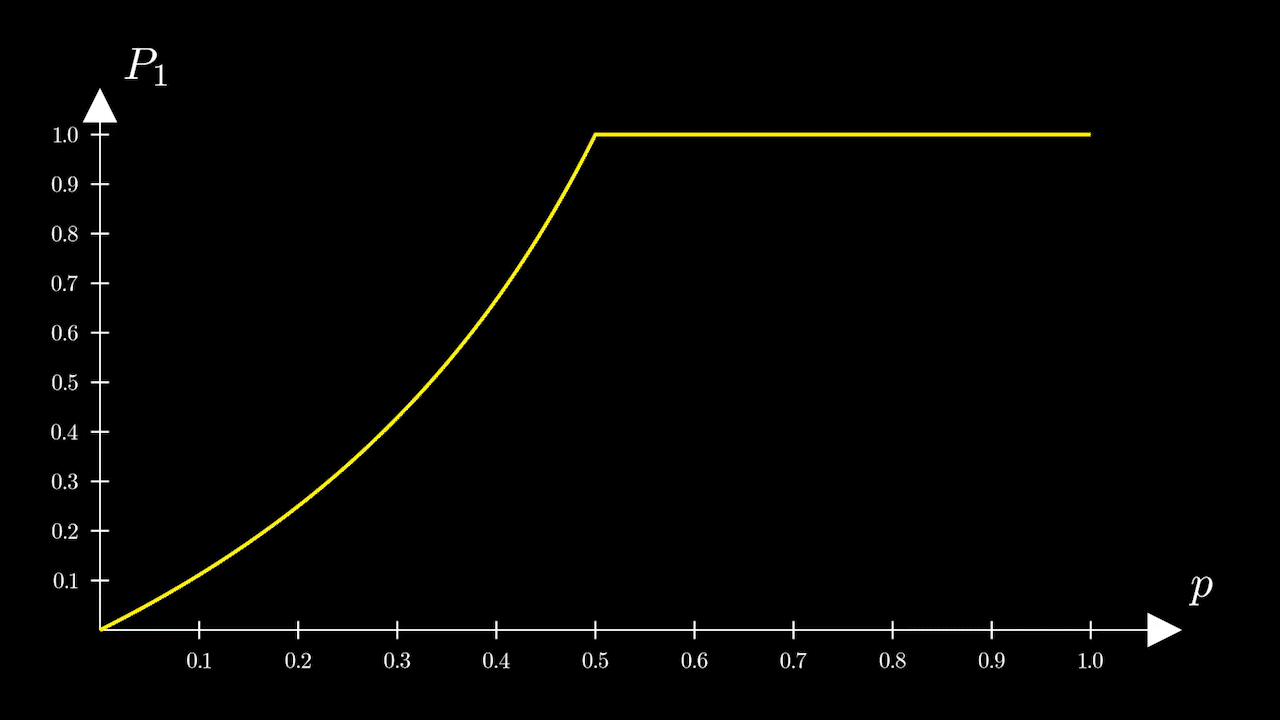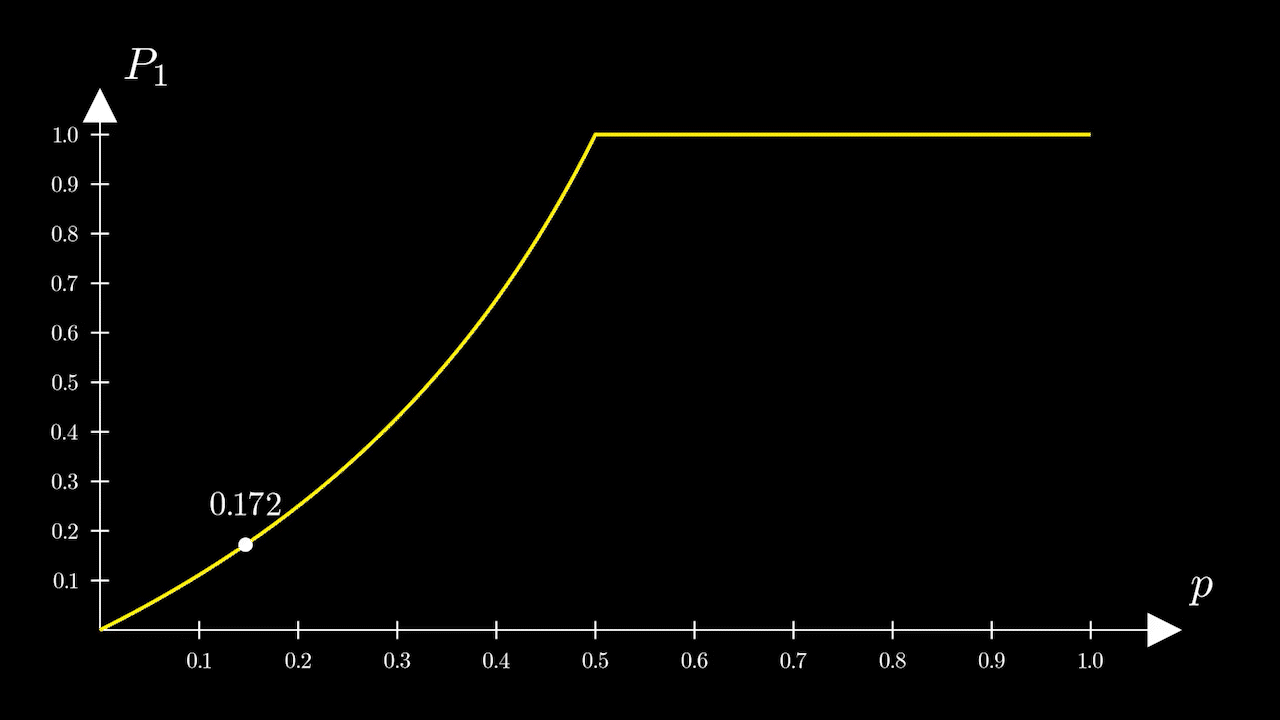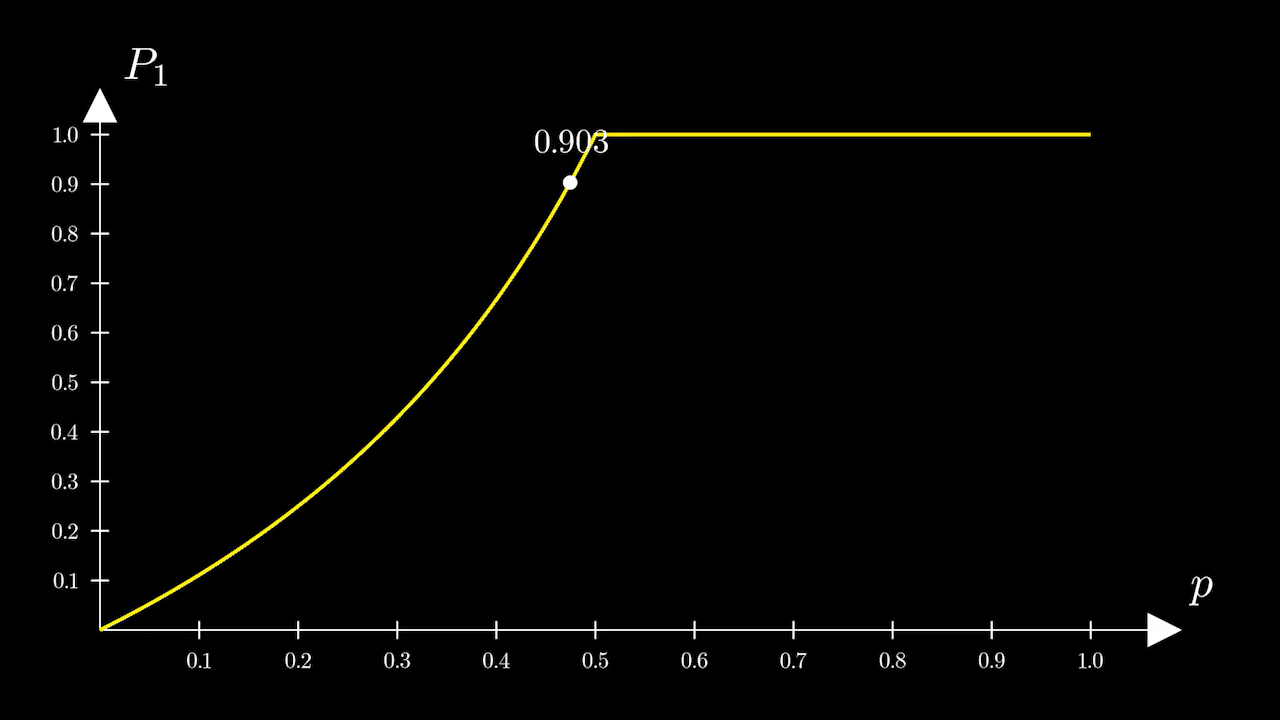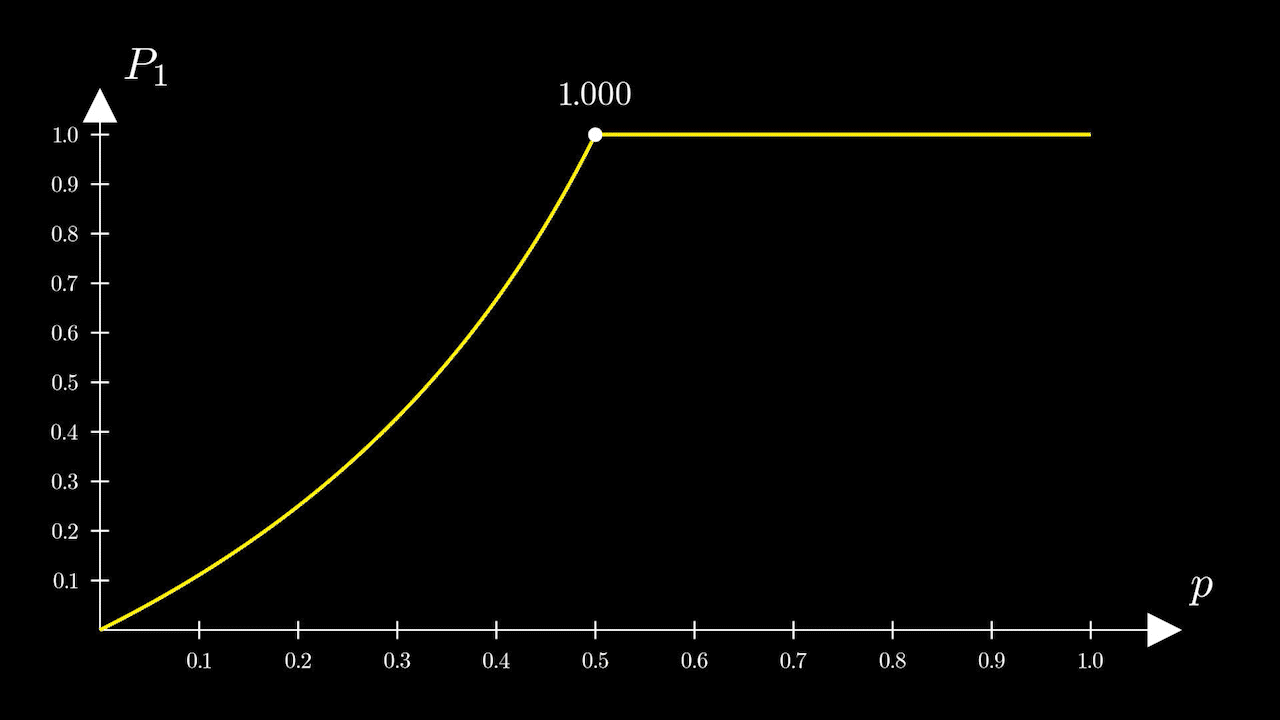
Рассмотрим график этой функции (рис. 2)

Рис. 2 График функции
Рис. 2 График функции

Посмотрим, как будет меняться вероятностьP_1с ростомp.

На промежутке[0,0.5)всё в принципе очевидно. Чем большеp,тем большеP_1.Переломный же момент наступает приp=0.5.

При p= 0.5,получаем, чтоP_1 =1,то есть пьяница точно упадет с обрыва.

На промежутке[0.5,1]функцияP_1принимает постоянное значение равное единице.

Таким образом, если вероятностьp \geq0.5,то пьяница точно упадет (другими словами, это достоверное событие).

Заключение

Вот такая интересная задача, при решении которой используются сразу несколько разделов математики.

Отдельно упомяну, что при значениеp=0.5,у нас возникает случайное блуждание, которое описывается с помощью цепи Маркова. Применительно к этой задаче, её описывает цепь Маркова со счетным множеством состояний, что сложнее, чем приведенное решение, но в каком-то смысле более правильное.

Кто хочет углубиться в эту тему, ниже различная литература.

Ссылки на литературу и различные источники

Основное:

[1] Пятьдесят занимательных вероятностных задач с решениями. Ф. Мостеллер.

[2] Конкретная математика. Основание информатики (1998). Р. Грэхем, Д. Кнут, О. Паташник.

Дополнительное:

[1] Блужданья по цепям Александр Гиль и Антон Петрунин.

[2] Вероятность и статистика в примерах и задачах. Том 2. Марковские цепи как отправная точка теории случайных процессов и их приложения. Кельберт М. Я., Сухов Ю. М.

Прочее:

Для создания графики использовался manimCE: https://github.com/manimCommunity/manim

Комментарии (65)


  1. lgorSL
    26.09.2022 22:15
    #0
    +17

    Кстати, к этой задаче есть ещё другой подход. Есть какое-то распределение вероятностей по шагам f(n, t), которое мы ищем, а так же краевое условие f(n, t) = 0. Можно сначала найти решение p(n, t) без краевых условий (как будто пропасти нет), а потом для учёта краевого условия сказать, что f(n, t) = p(n, t) - p(-n, t). Как будто за пропастью есть "анти-пьяница" с отрицательной вероятностью существования, и сложение вероятностей как раз даст 0 на границе пропасти.

    Для больших t распределение вероятностей будет похожим на распределение Гаусса. (если не смотреть на приколы с чётностью шагов). Если вероятность шага право выше шага влево, то центр гауссианы со временем будет двигаться вправо (как раз на разность вероятности шагнуть влево и вправо.). Идея с "отражением" функции для учёта краевого случая будет работать и тут, так что результат точно так же будет суммой положительной и отрицательной Гауссиан.

    Кстати, в жизни случается что-то похожее в гальванике - молекула металла случайно блуждает в электролите, но из-за электрического поля вероятность блуждания "в нужном направлении" будет выше, а при достижении поверхности молекула осядет на ней.


  1. lxsmkv
    26.09.2022 20:50
    #24769264
    -2

    Ставь лайк, если после этого стал немного больше уважать пьяниц :)


    1. beeruser
      26.09.2022 23:49
      #24769638
      +5

      Ставь лайк, если ходил пьяным по краю обрыва.


      1. sappience
        27.09.2022 04:38
        #24769874
        +30

        Ставь лайк если ходил с p >= 0.5 бесконечно долго, но так и не упал.


        1. toxicdream
          28.09.2022 08:35
          #24772896

          У вас какая-то неправильная бесконечность!


        1. kaka888
          29.09.2022 06:46
          #24775076

          С бесконечным количеством шагов будет неопределенный исход


  1. Akina
    26.09.2022 21:50
    #24769406

    При p= 0.5,получаем, чтоP_1 =1,то есть пьяница точно упадет с обрыва.

    Таким образом, если вероятностьp \geq0.5,то пьяница точно упадет (другими словами, это достоверное событие).

    Задача вероятностная. ПриP =1 вероятность того, что ВСЕ шаги пьяницы будут в сторону от обрыва, пусть и мала, но тем не менее ненулевая. Вероятность того, что на любом шаге количество шагов "от" будет не менее количества шагов "до" - не просто ненулевая, а гораздо больше предыдущей, хотя и по-прежнему исчезающе мала. А потому достоверным это событие назвать ну никак нельзя.


    1. BigBeaver
      26.09.2022 21:56
      #24769418
      +1

      Только, если число шагов ограничено.


    1. Quark-Fusion
      26.09.2022 22:03
      #24769428
      +2

      при бесконечном количестве шагов?


    1. Monotirg Автор
      26.09.2022 22:59
      #24769534
      +2

      Наполовину вы правы. Если ограничить количество шагов пьяницы, то, действительно, событие "пьяница упал с обрыва" не является достоверным (за исключением тривиального случая, когдаp=1). Если же не ограничивать количество шагов, то событие "пьяница упал с обрыва" будет достоверным приp\geq0.5, потому что приp\geq 0.5множество элементарных событий состоит только из этого события.


      1. Rsa97
        27.09.2022 00:33
        #24769686

        Это только для сферического пьяницы в вакууме. Реальный пьяница может не дожить до падения с обрыва, а умереть раньше от другой причины.


        1. Pro-invader
          27.09.2022 07:31
          #24769986
          +1

          Скорее не умереть, а уснуть, поэтому не упасть.


          1. snaiper04ek
            27.09.2022 12:19
            #24770806

            Скорее не "уснуть, поэтому не упасть ", а упасть в сторону от обрыва, после чего уснуть


            1. middle
              28.09.2022 08:17
              #24772868

              Или упасть в обрыв и уснуть вечным сном.


      1. Akina
        27.09.2022 08:11
        #24770026
        +1

        Вероятность того, что ВСЕ шаги пьяницы будут сделаны в направлении ОТ обрыва, равна (1-p)^n, где n - количество шагов. Верно? И хотя предел данного выражения при n стремящемся к бесконечности равен нулю, значение этого выражения тем не менее не ноль, а некое положительное, хотя и исчезающе малое, значение. Верно? То есть вероятность, что пьяница не упадёт потому, что будет все шаги делать в сторону от обрыва - ненулевая. Верно?

        Или есть возражения? только, пожалуйста, не на бытовом уровне...

        Мне самому в своё время с трудом далось понимание, что "если длина палки, измеренная портновским метром, равна 1 метру, то существует ненулевая вероятность, что длина палки 2 метра".


        1. auddu_k
          27.09.2022 08:32
          #24770082
          +2

          А можно чуть подробнее про палку, очень уж интересно ????


        1. BigBeaver
          27.09.2022 08:44
          #24770102
          +12

          Вы как-то слишком легко обращаетесь со словом «все» в разговоре о бесконечностях. Правильно ваше утверждение будет звучать так: «в любой момент времени при сколь угодно большом n всегда остается некоторая вероятность, что пьяница еще не упал».


        1. vadimr
          27.09.2022 10:24
          #24770382
          +2

          Вероятность любой отдельной реализации в бесконечном пространстве возможных событий (в том числе и вероятность бесконечного числа шагов направо) строго равна нулю.

          И тему насчёт своего понимания случая с палкой поясните, пожалуйста. У методически правильно используемого портновского метра есть погрешность измерения, больше которой получиться не может.


        1. anatolii_kostrygin
          27.09.2022 11:57
          #24770708
          +8

          Нет, вы неправильно обращаетесь с предельным переходом. Расширяя комментарий от @BigBeaver, представьте, что мы с вами заключаем пари - если пьяница упадёт за nшагов, то вы мне платите 1 рубль, если пьяница не упадёт - я вам плачу Xрублей. При этом сначала вы выбираете число Xи говорите мне, а потом я выбираю число n. При каком значении Xигра будет для вас выигрышна в среднем? Ни при каком: я всегда смогу предложить такое конечное значение n(зависящее от X), что пьяница не упадёт с вероятностью меньшей 1 / X.

          Именно это и понимается под утверждение "пьяница гаратнированно упадёт через бесконечное количество шагов" - это просто удобная фигура речи, позволяющая опускать несколько тяжеловесную формулировку предела на бесконечности.

          Операция "подождать бесконечное число шагов" в реальном мире в общем-то неопределена - даже с Большого взрыва прошло конечное число секунд.


    1. qw1
      27.09.2022 11:07
      #24770546
      +2

      А потому достоверным это событие назвать ну никак нельзя
      Вероятность достоверного события = 1, но обратное верно ли?
      Например, вероятность случайного выбора любого (заранее заданного) числа на отрезке [0,1] равна нулю, но как только эксперимент проведён, какое-то число точно выпало, хотя вероятность его выпадения строго равна 0.


      1. Aldrog
        27.09.2022 14:50
        #24771310
        +2

        Вот мне тоже этот пример вспомнился. Если я ничего не путаю, в задаче про пьяницу тот же случай, когда вероятность падения строго равна единице, но достоверным событие не является.


        1. BigBeaver
          27.09.2022 15:02
          #24771340

          Оно не является достоверным для каждого конкретного числа шагов (по аналогии с каждой конкретной точке на отрезке).


          1. Aldrog
            27.09.2022 15:36
            #24771452
            +1

            Для любого конечного числа шагов оно и вероятность равную единице не имеет. А на бесконечном числе шагов вероятность равна единице, но событие является «почти достоверным», но не достоверным.

            Так же как при выборе точки на отрезке вещественных чисел попадание в конкретное число имеет нулевую вероятность, называется «почти невозможным», но произойти всё-таки может.


            1. BigBeaver
              27.09.2022 16:28
              #24771546

              Разумется — вероятность равную единице имеет интеграл по лучу от нолу до бесконечности. Собственно, это и есть сумма ряда, посчитанная в статье.

              называется «почти невозможным», но произойти всё-таки может.
              Ну так здесь идея в том, что на бесконечном луче нет понятия «все» (по крайне мере в бытовом смысле). То есть, как бы далеко он не уползал от обрыва, всегда остается вероятность упасть.

              Потому здесь на самом деле намного интереснее выглядят исходы, когда вероятность меньше единицы. Я бы сказал, что существование шанса того, что можно вообще никогда не упасть интуитивно кажется странным.


              1. qw1
                27.09.2022 16:48
                #24771622

                Хороший вопрос.

                Если «вероятность упасть» равна p1, то «вероятность не упасть» равна ли (1-p1)?

                Вероятность упасть (вообще когда-либо) есть сумма вероятностей:
                — вероятность упасть на 1-м шаге
                — вероятность упасть на 2-м шаге
                …

                Вероятность не упасть есть произведение вероятностей:
                — вероятность не упасть на 1-м шаге
                — вероятность не упасть на 2-м шаге
                …

                Если суммировать ряды мы худо-бедно умеем, то как обстоят дела с бесконечными произведениями?

                Вполне возможно, что доказуемы оба утверждения:
                — вероятность упасть равна 0 < p1 < 1 (например, для любой точки в левой части графика статьи);
                — вероятность не упасть равна 0.
                при одном и том же начальном p.


                1. Cerberuser
                  27.09.2022 16:53
                  #24771646
                  +3

                  Если суммировать ряды мы худо-бедно умеем, то как обстоят дела с бесконечными произведениями?

                  Точно так же - сходятся к пределу частичных произведений, как ряд к пределу частичных сумм. Ну или, если я правильно помню матан, сводятся к ряду через взятие логарифма.

                  Вполне возможно, что доказуемы оба утверждения:

                  — вероятность упасть равна 0 < p1 < 1 (например, для любой точки в левой части графика статьи);

                  — вероятность не упасть равна 0.

                  Проблема в том, что при бесконечном количестве шагов эти исходы исчерпывают всё пространство событий. А значит, сумма их вероятностей, какими бы они ни были, будет 1, чисто по определению.


                  1. qw1
                    27.09.2022 16:58
                    #24771666
                    +1

                    Проблема в том, что при бесконечном количестве шагов эти исходы исчерпывают всё пространство событий. А значит, сумма их вероятностей, какими бы они ни были, будет 1, чисто по определению.
                    Для бесконечных множеств такие предположения делать опасно. Тут и равенство количества чётных чисел количеству всех целых чисел, и парадокс Банаха-Тарского.


                    1. Cerberuser
                      27.09.2022 17:05
                      #24771688

                      То есть, Вы утверждаете, что существует событие (бесконечная последовательность шагов), которое не относится к одному из этих двух исходов? Если нет - то бесконечность не играет никакой роли, у нас просто есть разбиение множества на две части. Худшее, что может случиться, - одна из этих частей может оказаться неизмеримой (и то, не помню с ходу, возможно ли, чтобы неизмеримой была ровно одна из них); но если обе измеримы, то сумма их мер (~вероятностей) будет равна мере всего множества (~единице, по определению вероятности).


                      1. qw1
                        27.09.2022 17:23
                        #24771748
                        +1

                        А вы утверждаете, что нет такого события?
                        Но как вы проверите?

                        У вас нет бесконечного времени, чтобы смоделировать исход шагов для любой бесконечной последовательности.

                        Можно как-то алгоритмически конструировать такие последовательности, и привязать их к каким-то недоказаным гипотезам. Например, мы не упадём, если количество простых чисел-близнецов бесконечно. Иначе упадём.
                        И тогда аналитически вы не предскажете исход, а моделирование потребует бесконечных ресурсов.

                        А можно ещё попробовать привязать к невычислимой функции. Как-никак, бесконечных последовательностей — континуум, а алгоритмов — счётное число. Значит, есть последовательность, которую нельзя задать алгоритмически. И как вы для неё посчитаете исход?


                      1. Cerberuser
                        27.09.2022 18:14
                        #24771892

                        А вы утверждаете, что нет такого события?

                        Да, тривиальным образом: из двух исходов один реализуется, когда шаг, на котором происходит падение, существует, второй - когда этот шаг не существует. Вы, я так понимаю, различаете случаи "шаг доказуемо существует" и "шаг существует, но невычислим", и считаете, что во втором случае факт наличия падения не определён?


                      1. qw1
                        27.09.2022 19:34
                        #24772048

                        Вы считаете, что исхода всегда два: падает или не падает. Это похоже на классификацию любых формул на истинные и ложные. Но есть ещё класс недоказуемых. Я думаю, на континууме последовательностей вы почти наверное попадёте именно на такую последовательность. Почему недоказуемую? Потому что вы её не можете записать, а значит, и проанализировать аналитически.


                      1. Cerberuser
                        27.09.2022 20:05
                        #24772112
                        +1

                        Я считаю, что между фактами "X существует" и "X не существует" отсутствует третья альтернатива, да. Каждый из них отдельно распадается на случаи "...и это доказуемо" и "...и это недоказуемо", но для факта существования это незначимо.


                      1. qw1
                        27.09.2022 21:36
                        #24772266

                        А как же теорема о неполноте?

                        Это возвращаясь к утверждению «Вполне возможно, что доказуемы оба утверждения...» Не удивлюсь, если так и есть.


                      1. Cerberuser
                        28.09.2022 05:15
                        #24772760

                        Теорема о неполноте гласит, что существуют утверждения, истинные, но недоказуемые. На факт наличия/отсутствия истинности она никак не влияет, он по-прежнему бинарен.


                      1. qw1
                        28.09.2022 10:03
                        #24773072

                        Если для какой-то последовательности шагов X невозможно доказать, приводит она к падению, или нет, что можно сказать об истинности утверждения «Последовательность X приводит падению»?


                      1. Cerberuser
                        28.09.2022 10:07
                        #24773080

                        А зачем о нём что-то говорить? Повторюсь - доказуемость истинности/ложности отличается от самой истинности/ложности.


                      1. qw1
                        28.09.2022 10:07
                        #24773082

                        Хотя, если так подумать, это можно сказать про любую недоказанную пока гипотезу. Истинна она или ложна, мы не знаем, но верим, что когда-нибудь узнаем.


                      1. BigBeaver
                        27.09.2022 20:36
                        #24772158

                        В общем случае вы, наверное, правы, но в контексте обсуждаемой задачи это уже эзотерика какая-то, кмк.


                      1. toxicdream
                        28.09.2022 08:39
                        #24772906

                        Очередной спор на тему 0,9(9) = 1


                1. vadimr
                  27.09.2022 17:49
                  #24771814

                  Вопрос в том, что нулевая вероятность на бесконечном пространстве событий не означает невозможности события.


      1. Vapekreng
        27.09.2022 17:27
        #24771754

        Здесь все упирается как раз в то, как вы сделаете выбор? За конечное время можно описать только конечное количество чисел. По факту, нет возможности выбрать из бесконечного количества чисел


        1. qw1
          27.09.2022 17:38
          #24771782

          Теория множеств не работает со временем.
          В какой-то момент я планирую сделать выбор, а в другой момент я уже выбрал.


          1. Vapekreng
            27.09.2022 17:59
            #24771848

            Вы выбрали число, ок. Какое именно? Вам же нужно ответить на этот вопрос хотя бы для себя. Может вы назовете число, может, зададите через формулу, опишете его, но выбор должен описывать ваше число однозначно. На описание числа уходит время, а вот время, как раз, конечная величина, следовательно, вы можете описать число с конечной точностью. Множество чисел, которые вы можете описать за всю свою жизнь это очень большое, но конечное множество


            1. qw1
              27.09.2022 19:38
              #24772052

              Тот я, который живёт в физическом мире, не может выбрать действительное число.
              А тот я, из идеального мира, мы про него запишем «выбрал число a, про которое мы ничего не знаем». А если по условиям задачи нужно как-то взаимодействовать с этим числом, все взаимодействия будут прописаны в условии. Пока нет никаких ограничений, нам достаточно знать, что это число a.


              1. Vapekreng
                27.09.2022 20:23
                #24772140

                Разве не вы выше написали:
                Например, вероятность случайного выбора любого (заранее заданного) числа на отрезке [0,1] равна нулю, но как только эксперимент проведён, какое-то число точно выпало, хотя вероятность его выпадения строго равна 0.

                Вот я и прошу описать мне, как вы в эксперименте выберете и зададите число. Будете кидать кубик? Спрашивать прохожих? Писать числа от балды? Использовать генератор случайных чисел?
                Да, чисел на этом отрезке бесконечное количество, но, в данном случае, идет речь только о числах, которые могут быть выбраны, а их конечное (хоть и очень большое) число. Ограничение накладывается не множеством, а необходимостью выбора


                1. BigBeaver
                  27.09.2022 20:40
                  #24772164
                  +2

                  Вообще, сравнение априорных и апостериорных вероятностей штука неблагодарная. Ну и в целом теорвер для «любящих в интуицию» насилие жуткое.


                1. qw1
                  27.09.2022 21:38
                  #24772272

                  Мы же тут математикой занимаемся? То есть, абстрактные задачки решаем.
                  Вот и будет в задачке формулировка: пользователь хабра qw1 выбрал случайное число из отрезка [0;1]. А как он это сделал — это вне абстракции.


  1. lgorSL
    26.09.2022 22:15
    #24769450
    +17

    Кстати, к этой задаче есть ещё другой подход. Есть какое-то распределение вероятностей по шагам f(n, t), которое мы ищем, а так же краевое условие f(n, t) = 0. Можно сначала найти решение p(n, t) без краевых условий (как будто пропасти нет), а потом для учёта краевого условия сказать, что f(n, t) = p(n, t) - p(-n, t). Как будто за пропастью есть "анти-пьяница" с отрицательной вероятностью существования, и сложение вероятностей как раз даст 0 на границе пропасти.

    Для больших t распределение вероятностей будет похожим на распределение Гаусса. (если не смотреть на приколы с чётностью шагов). Если вероятность шага право выше шага влево, то центр гауссианы со временем будет двигаться вправо (как раз на разность вероятности шагнуть влево и вправо.). Идея с "отражением" функции для учёта краевого случая будет работать и тут, так что результат точно так же будет суммой положительной и отрицательной Гауссиан.

    Кстати, в жизни случается что-то похожее в гальванике - молекула металла случайно блуждает в электролите, но из-за электрического поля вероятность блуждания "в нужном направлении" будет выше, а при достижении поверхности молекула осядет на ней.


    1. BigBeaver
      26.09.2022 22:17
      #24769456
      +2

      Ну вообще, это и есть задача про одномерное броуновское движение.


    1. iShrimp
      27.09.2022 19:27
      #24772038
      +2

      В непрерывном виде получится уравнение, аналогичное уравнению теплопроводности с граничными условиями 1 типа (Дирихле). Положим, что в точке х=0 отводится всё тепло (или уничтожаются все пьяницы), соответственно u(0, t) = 0. Такая задача действительно легко решается путём "помещения" пьяницы в точку х=1 и антипьяницы в точку х=-1 и свёртки с ядром Гаусса по всей вещественной оси.

      Интересно, что подобным образом можно решить и граничную задачу 2 типа (Неймана), когда в точке х=0 находится непреодолимый барьер и, соответственно, поток равен нулю (∂u/∂x = 0 при х = 0). В этом случае мы "помещаем" "положительных" пьяниц в точки х=1 и х=-1 и аналогично вычисляем свёртку с ядром Гаусса.


  1. mphys
    26.09.2022 23:28
    #24769598
    +2

    В чем вы делали такие шикарные анимации?


    1. Monotirg Автор
      26.09.2022 23:38
      #24769618
      +8

      Использовал только библиотеку manimCE для Python. В конце статьи есть ссылка на неё.


    1. egaxegax
      27.09.2022 12:01
      #24770726

      Adobe Premiere Pro 2022.0 (Windows). Внутри GIF-файла анимации в XML-заголовке написано.


      1. Monotirg Автор
        27.09.2022 17:30
        #24771762
        +1

        Через Adobe Premiere Pro я делал GIF, потому что каждая анимация изначально была в формате mp4.


  1. gremlin244
    27.09.2022 03:02
    #24769840
    +5

    Как далекий от математики и близкий к пьянству человек, имею заметить что на практике если поставить пьяницу на краю обрыва и заставить шагать, вероятность p должна постепенно снижаться, ведь он будет трезветь:) И если внести в условия, что скажем за каждый шаг p снижается на 0.01, то даже при стартовом p = 0.99, у нашего незадачливого пьяницы должна быть ненулевая, хоть и очень мизерная вероятность выжить)


    1. iShrimp
      27.09.2022 19:39
      #24772056

      А при удалении от пропасти p вновь повышается, так как герою задачи может попасться ларёк со спиртным? Значит, математическая модель пьяницы неполная.


  1. Refridgerator
    27.09.2022 10:51
    #24770480
    +2

    Как решать такую задачу чуть ближе к реальности — когда пьяница может передвигаться в двух измерениях? А вместо пропасти, например, открытый канализационный люк.


    1. rjhdby
      27.09.2022 11:06
      #24770544
      -1

      ...и на четырёх конечностях. С таким условием, даже если он "шагнёт" в пропасть - это не будет означать автоматического падения.


    1. Monotirg Автор
      27.09.2022 17:45
      #24771798
      +1

      В марковских цепях есть тема: "Cлучайные блуждания на кубических решетках", в ней как раз и разбираются подобного рода задачи. Например, в книге "Вероятность и статистика в примерах и задачах. Том 2. Марковские цепи как отправная точка теории случайных процессов и их приложения. Кельберт М. Я., Сухов Ю. М." на 59 стр. разбирается эта тема.


  1. maty
    27.09.2022 12:09
    #24770770
    +4

    В целом было интересно, особенно про связь с числами Каталана.

    Тем не менее, есть два наблюдения.

    1. Формулу для P1 можно упросить, поскольку под корнем полный квадрат (2p - 1)^2. Мне кажется приятнее видеть |2p - 1| в этой формуле.

    2. Исходную задачу можно решить много проще, если выводить рекуррентное соотношение сразу для вероятности Pn. Оно имеет вид

      (1) P(n) = p P(n-1) + (1-p) P(n+1)

      Пространство решений уравнения (1) двумерно и при p отличном от 0.5 общее решение имеет вид P(n) = A (p / (1-p))^n + B. Для поиска базиса нужно просто искать решения вида n^a. При p=0.5 общее решение имеет вид A +B n.

      Далее, из условий (P(0) = 1, P(n) <= 1) и непрерывности решения по p, находим, что

      P(n) = (p / (1 - p))^n при p< 0.5 и

      P(n) = 1 при p>= 0.5


    1. Monotirg Автор
      27.09.2022 18:20
      #24771906

      Исходную задачу можно решить много проще, если выводить рекуррентное соотношение сразу для вероятности Pn.

      Кстати, аналогичный подход используется, если вводить цепь Маркова.


  1. Ontaelio
    27.09.2022 13:49
    #24771120

    Вообще, в задаче неслучайно указан пьяница, а не слепой инженер-математик, например. Вероятность того, что он навернется - либо да, либо нет.

    (но вот за числа Каталана спасибо)


  1. voted
    27.09.2022 14:48
    #24771296
    +1

    Не нашёл решения исходной задачи (на картинке)

    при p = 1/3 => P1 = 0,5.


  1. thevlad
    27.09.2022 17:28
    #24771756
    +1

    Все уже давно придумано до нас, и решается в общем случаи, https://en.wikipedia.org/wiki/Birth–death_process не надо велосипедов.


  1. yadiver
    27.09.2022 17:54
    #24771828

    а чисто по логике, разве вероятность может быть ниже 1/3 ? У первого шага в сторону пропасти именно такая вероятность. Если первый шаг в другую сторону, то дальше эта вероятность стремится к нулю(если нет ограничения по рассчитываемому кол-ву шагов), но учитывая первый шаг - не может быть ниже 1/3


    1. Monotirg Автор
      27.09.2022 18:05
      #24771872
      +1

      а чисто по логике, разве вероятность может быть ниже 1/3 ?

      Если я правильно понял вопрос, то может ли вероятностьP_1быть меньше p. Нет, не может, потому что верно следующее неравенство

      p = p_1 \leq p_1 + p_{3} + p_5 +\ldots = P_{1}.