Статья посвящена реализации алгоритма Гаусса для решения системы линейных алгебраических уравнений на языке Java.
Рассмотрим математическую теорию. Система линейных уравнений может иметь одно решение, бесконечно много решений или же быть несовместной (не иметь решений). Не все методы решения СЛАУ могут справится с вторым случаем, когда система имеет бесконечно много решений. Например, метод Крамера и матричный метод не применимы, но метод Гаусса вполне можно использовать.
Алгоритм можно условно разделить на два этапа:
В первом этапе образуются нули ниже или выше главной диагонали, за счет использования элементарных преобразований матрицы. На втором этапе находят неизвестные начиная с конца. Подробную теорию можно посмотреть по ссылке: метод Гаусса, поэтому с теорией пожалуй все. Перейдем к реализации.
Начнем с постановки задачи:
Начнем с написания интерфейса, который должно реализовывать каждое уравнение:
Здесь все должно быть ясно, N некоторый наследник Number'а, T — некоторый тип, реализующий данный интерфейс (рекурсивные дженерики). Метод addEquation(T item) позволяет прибавить каждый элемент уравнения item к каждому своему элементу. Остальные методы работают аналогично.
Теперь рассмотрим класс системы уравнений. Как видно в листинге ниже, он дженеризирован так же, как и интерфейс Gauss и содержит методы для удобного доступа к приватному списку содержащих в себе уравнений.
Теперь можно приступать к реализации «частного случая» структуры уравнения. Создадим класс MyEquation, реализующий наш интерфейс. Пусть наследником Number'а будетсверхточный класс Float (на практике лучше брать Double). Обратите внимание, что в методе addEquation(MyEquation item) используется объект класса ListIterator, позволяющий изменять элементы перебираемого списка.
Теперь имеем полноценную структуру данных, реализующую систему уравнений. Составим алгоритм который будет принимать некоторый объект, реализующий интерфейс Gauss, затем вызывая нужные методы приведет матрицу к нужному виду.
Алгоритм простой, найти нужный коэффициент, домножить на него i-ю строку (i=0..n-1), и прибавить ее к j-й строке (j=i..n). Заметьте, алгоритм не знает как именно реализуются методы findCoefficient, mul и addEquation, это придает коду бОльшую гибкость, т.к. при потребности изменить способы манипуляции уравнениями (строками), будут изменены только реализации трех вышеупомянутых методов, а главный алгоритм останется нетронутым.
Почти все. Осталось запустить это все в методе main:
Запустим это чудо, что бы проверить корректность работы…
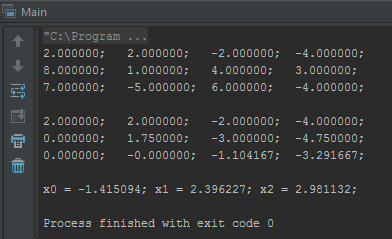
Это все. Исходники можно скачать на github'е.
Метод Гаусса не очень поддается обобщенному программированию (как видите обратный ход выполнен отдельно), однако вышла своеобразная реализация которая, надеюсь, поможет кому то лучше разобраться в искусстве использования интерфейсов и дженериков.
Теоретические сведения
Рассмотрим математическую теорию. Система линейных уравнений может иметь одно решение, бесконечно много решений или же быть несовместной (не иметь решений). Не все методы решения СЛАУ могут справится с вторым случаем, когда система имеет бесконечно много решений. Например, метод Крамера и матричный метод не применимы, но метод Гаусса вполне можно использовать.
Алгоритм можно условно разделить на два этапа:
- Прямой ход
- Обратный ход
В первом этапе образуются нули ниже или выше главной диагонали, за счет использования элементарных преобразований матрицы. На втором этапе находят неизвестные начиная с конца. Подробную теорию можно посмотреть по ссылке: метод Гаусса, поэтому с теорией пожалуй все. Перейдем к реализации.
Реализация
Начнем с постановки задачи:
- нам нужно создать программу, реализующую систему линейных уравнений в виде некоторой структуры данных, используя приемы обобщенного программирования. Система должна содержать коэффициенты производного типа от класса Number (т.е. Float, Integer, Double и т.д.)
- Запрограммировать алгоритм, который получив на вход структуру данных системы образует нули ниже главной диагонали
Начнем с написания интерфейса, который должно реализовывать каждое уравнение:
package gauss;
public interface Gauss<N extends Number, T extends Gauss<N, T>> {
public void addEquation(T item);
public void mul(N coefficient);
public N findCoefficient(N a, N b);
public N at(int index);
public int size();
}
Здесь все должно быть ясно, N некоторый наследник Number'а, T — некоторый тип, реализующий данный интерфейс (рекурсивные дженерики). Метод addEquation(T item) позволяет прибавить каждый элемент уравнения item к каждому своему элементу. Остальные методы работают аналогично.
Теперь рассмотрим класс системы уравнений. Как видно в листинге ниже, он дженеризирован так же, как и интерфейс Gauss и содержит методы для удобного доступа к приватному списку содержащих в себе уравнений.
package gauss;
import java.util.ArrayList;
import java.util.List;
public class LinearSystem<N extends Number, T extends Gauss<N, T>> {
private List<T> list = new ArrayList<T>();
public T get(int index){
return list.get(index);
}
public void push(T elem){
list.add(elem);
}
public int size(){
return list.size();
}
public N itemAt(int i, int j){
return list.get(i).at(j);
}
}
Теперь можно приступать к реализации «частного случая» структуры уравнения. Создадим класс MyEquation, реализующий наш интерфейс. Пусть наследником Number'а будет
package gauss;
import java.util.ArrayList;
import java.util.List;
import java.util.ListIterator;
import java.util.Random;
public class MyEquation implements Gauss<Float, MyEquation> {
private List<Float> equation = new ArrayList<Float>();
public List<Float> getEquation(){
return equation;
}
public void generate(int size){
if (size < 2) size = 2;
this.equation.clear();
for (int i = 0; i < size; i++){
Random random = new Random();
this.equation.add((float) (random.nextInt()%10) + 1);
}
}
@Override
public int size(){
return equation.size();
}
@Override
public void addEquation(MyEquation item){
ListIterator<Float> i = equation.listIterator();
ListIterator<Float> j = item.getEquation().listIterator();
for(; i.hasNext() && j.hasNext();){
Float a = i.next();
Float b = j.next();
i.set(a + b);
}
}
@Override
public void mul(Float coefficient){
for(ListIterator<Float> i = equation.listIterator(); i.hasNext();){
Float next = i.next();
i.set(next * coefficient);
}
}
@Override
public Float findCoefficient(Float a, Float b){
if (a == 0.0f) return 1.0f;
return -b/a;
}
@Override
public Float at(int index){
return equation.get(index);
}
}
Теперь имеем полноценную структуру данных, реализующую систему уравнений. Составим алгоритм который будет принимать некоторый объект, реализующий интерфейс Gauss, затем вызывая нужные методы приведет матрицу к нужному виду.
package gauss;
public class Algorithm<N extends Number, T extends Gauss<N, T>> {
LinearSystem<N, T> list = null;
public Algorithm(LinearSystem<N, T> system){
list = system;
}
public void calculate() throws NullPointerException, ArithmeticException{
if (list == null){
throw new NullPointerException("LinearSystem<N, T> instance equal null");
}
if (!checkSystem(list)){
throw new ArithmeticException("Incorrect system for Gauss Method");
}
for(int i = 0; i < list.size() - 1; i++){
for(int j = i + 1; j < list.size(); j++){
N k = list.get(j).findCoefficient(list.get(j).at(i), list.get(i).at(i));
list.get(j).mul(k);
list.get(j).addEquation(list.get(i));
}
}
}
private boolean checkSystem(LinearSystem<N, T> system){
if (system.size() < 2) return false;
for(int i = 0; i < system.size(); i++){
if (system.get(i).size() != (system.size() + 1)){
return false;
}
}
return true;
}
}
Алгоритм простой, найти нужный коэффициент, домножить на него i-ю строку (i=0..n-1), и прибавить ее к j-й строке (j=i..n). Заметьте, алгоритм не знает как именно реализуются методы findCoefficient, mul и addEquation, это придает коду бОльшую гибкость, т.к. при потребности изменить способы манипуляции уравнениями (строками), будут изменены только реализации трех вышеупомянутых методов, а главный алгоритм останется нетронутым.
Почти все. Осталось запустить это все в методе main:
import gauss.Algorithm;
import gauss.MyEquation;
import gauss.LinearSystem;
public class Main {
private static final int DEFAULT_EQUATIONS_NUMBER = 2;
private static final int DEFAULT_VARIABLES_NUMBER = 2;
public static void main(String args[]){
LinearSystem<Float, MyEquation> list = generateSystem();
printSystem(list);
int i, j;
Algorithm<Float, MyEquation> alg = new Algorithm<Float, MyEquation>(list);
try{
alg.calculate();
}catch (NullPointerException e){
System.out.println(e.getMessage());
System.exit(0);
}catch (ArithmeticException e){
System.out.println(e.getMessage());
System.exit(0);
}
Float [] x = new Float[DEFAULT_EQUATIONS_NUMBER];
for(i = list.size() - 1; i >= 0; i--) {
Float sum = 0.0f;
for(j = list.size() - 1; j > i; j--) {
sum += list.itemAt(i, j) * x[j];
}
x[i] = (list.itemAt(i, list.size()) - sum) / list.itemAt(i, j);
}
printSystem(list);
printVector(x);
}
public static LinearSystem<Float, MyEquation> generateSystem(){
LinearSystem<Float, MyEquation> list = new LinearSystem<Float, MyEquation>();
int i;
for (i = 0; i < DEFAULT_EQUATIONS_NUMBER; i++){
MyEquation eq = new MyEquation();
eq.generate(DEFAULT_VARIABLES_NUMBER + 1);
list.push(eq);
}
return list;
}
public static void printSystem(LinearSystem<Float, MyEquation> system){
for (int i = 0; i < system.size(); i++){
MyEquation temp = system.get(i);
String s = "";
for (int j = 0; j < temp.size(); j++){
s += String.format("%f; %s", system.itemAt(i, j), "\t");
}
System.out.println(s);
}System.out.println("");
}
public static void printVector(Float [] x){
String s = "";
for (int i = 0; i < x.length; i++){
s += String.format("x%d = %f; ", i, x[i]);
}System.out.println(s);
}
}
Запустим это чудо, что бы проверить корректность работы…

Это все. Исходники можно скачать на github'е.
Вывод
Метод Гаусса не очень поддается обобщенному программированию (как видите обратный ход выполнен отдельно), однако вышла своеобразная реализация которая, надеюсь, поможет кому то лучше разобраться в искусстве использования интерфейсов и дженериков.
Список использованной литературы:
Комментарии (6)

SirEdvin
08.11.2015 00:10Эм…
А как он, например, разделяет случай, когда у уравнения бесконечно много решений и нет решений?
Почему именно такой, а не диагональный или с поиском максимального элемента по модулю?
Ну а про дженерики. У меня где-то валялся обобщенный класс матриц и для него математические штуки… там в любом случае все печально выглядит.

SirEdvin
08.11.2015 00:21Так же, написанный вами метод, скорее всего, упадет на матрице вида:
1 0 0 0 0 1 0 1 0
Хотя у нее есть одно решение.
Ну и немного по коду…
throws NullPointerException, ArithmeticException
Не делайте так. Обе эти ошибки являются runtime exception и не предназначены для отлова. Если они так нужны в том месте, лучше написать свою или использовать new Exception(«Text»).
Так же в этом случае лучше не делать это через дженерики, потому что у примитивов существует boxing/un-boxing, который достаточно весомый. Куда эффективнее сделать просто для float.


vedenin1980
Если это лабораторная в институте, то вопросов нет. Если нужно для реальной работы с линейными уравнениями, вы не смотрели библиотеки вроде
math.nist.gov/javanumerics/jama
commons.apache.org/math
ojalgo.org
hubris.ucsd.edu/sstj
code.google.com/p/matrix-toolkits-java
code.google.com/p/efficient-java-matrix-library
la4j.org
?
vdmitriyev
Спасибо за ссылки. Не все доступны, вот рабочая ссылка для библиотеки matrix-toolkits-java — github.com/fommil/matrix-toolkits-java
alexeygrigorev
jblas забыли