Введение
В этой статье будет рассмотрена тема построения и работы с конечными полями (или полями Галуа), которые используются в криптографии, теории информации и кодирования и других науках, т.е. имеют широкое практическое применение. Сухую теорию о группах/кольцах/полях можно прочитать по ссылке Поля Галуа, а здесь будет больше практики и реализации на языке Scala.
Типы и ограничения
Для начала следует обсудить технические проблемы связанные с представлением полиномов в памяти, с учетом размеров типа Int в языке Scala. Требования сформулированы в списке ниже.
- Тип Int в Scala/Java имеет размер 32 бита
- Использовать можно биты: 0..30 — 31, поскольку 32-ой бит является знаковым
- Полиномы должны быть представлены числами в диапозоне 0..29
- Неприводимые полиномы (или модули) имеют диапозон 1..30
- Конечное поле имеет
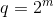 элементов
элементов
Реализация
Сначала опишем класс Polynomial, который реализует полином и 4 операции. Этот вид полинома является «полуфабрикатом» и не привязан к конечному полю.
class Polynomial(_p: Int) {
val polynomial: Int = _p
def order: Int = = {
...
}
def mul(p: Polynomial): Polynomial = {
...
}
def div(p: Polynomial): (Int, Int) = {
...
}
def add(p: Polynomial): Polynomial = {
...
}
def sub(p: Polynomial): Polynomial = {
...
}
override def toString: String = Integer.toBinaryString(this.polynomial)
}
Далее абстрактный класс FiniteField, который будет родителем полей Галуа. Внутри FiniteField содержится внутренний класс FiniteFieldPolynomial, такая структура позволяет обеспечить безопасность при проведении операций.
Безопасность заключается в том, что операции возможно производить только с полиномами из одного поля.
Обратите внимание на член modulo, это модуль (или же неприводимый полином) степени поля.
abstract class FiniteField(_initBitNumber: Int) {
type T = Polynomial
type GFPolynomial <: FiniteFieldPolynomial
protected val checkBitNumber: Int => Int = ???
val modulo: T
val bits: Int = checkBitNumber(_initBitNumber)
protected def createModulo(): Option[Int]
def createPolynomial(_initPolynomial: Int): FiniteFieldPolynomial
abstract class FiniteFieldPolynomial {
protected val p: T
def +(other: GFPolynomial): GFPolynomial
def -(other: GFPolynomial): GFPolynomial = {
this + other
}
def *(other: GFPolynomial): GFPolynomial
def /(other: GFPolynomial): GFPolynomial = this * other.mulInverse
def addInverse: GFPolynomial = self
def mulInverse: GFPolynomial
def self: GFPolynomial
}
}
Важным этапом построения поля Галуа есть вычисление неприводимых полиномов степени поля, а так же выбор одного из них. С математикой данного процесса можно ознакомиться по ссылке Неприводимые полиномы.
Неприводимый полином будет использоваться для операций умножения и деления, точно так же как простое число для числового поля
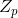 .
.Иными словами, неприводимыые полиномы играют ту же роль во множествах полиномов, что и простые числа во множествах целых чисел.
Упрощенный код для нахождения множества неприводимых полиномов представлен ниже. Алгоритм следующий:
- если требуемый порядок deg равен 1, то просто возвратить готовый список неприводимых полиномов степени 1
- в случае, когда требуемый порядок более 1:
- сгенерировать все полиномы порядка deg (пусть P множество этих полиномов)
- находим список неприводимых полиномов степени
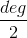 (пусть G множество этих неприводимых полиномов)
(пусть G множество этих неприводимых полиномов)
- если полином
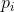 не делится без остатка ни на один полином
не делится без остатка ни на один полином 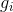 , то он является неприводимым, значит нужно добавить
, то он является неприводимым, значит нужно добавить 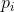 в результирующий список полиномов-модулей
в результирующий список полиномов-модулей
object IrreduciblePolynomials{ private def check(p: Int, list: List[Int]): Boolean = { val pol = Polynomial(p) list.foreach((item: Int) => { val i = Polynomial(item) if ((pol div i)._2 == 0){ return false } }) true } def calcIrreducible(_deg: Int): List[Int] = { def calc(deg: Int): List[Int] = { if (deg == 1) return List[Int](2, 3) // d > 2 var resultList = ListBuffer[Int]() // generate all polynomials of degree d val n = 1 << deg val nd = if (_deg.equals(deg)) deg >> 1 else deg - 1 val list: List[Int] = calc(nd) for(i <- 0 until n){ val t = i ^ n // polynomial of P set, for testing if (check(t, list)) resultList += t } resultList.toList ::: list } if (_deg < 1) return Nil calc(_deg).filter(_ >= (1 << _deg)) } }
Осталось реализовать конкретный класс-наследник FiniteField, который будет готовым конечным полем.
class GaloisField(_initBitNumber: Int = FiniteField.DEFAULT_BIT_NUMBER) extends FiniteField(_initBitNumber) { override val modulo: Polynomial = ... protected def createModulo(): Option[Int] = { val list = IrreduciblePolynomials(this.bits) list.headOption } def createPolynomial(_initPolynomial: Int): GFPolynomial = { ... } def createPolynomial(_binInitPolynomial: String): GFPolynomial = { ... } class GFPolynomial private[GaloisField](_p: Int, _m: Int) extends FiniteFieldPolynomial with Comparable[GFPolynomial]{ override def equals(other: Any): Boolean = other match { case other: GFPolynomial => this.p.polynomial == other.p.polynomial case _ => false } override protected val p = Polynomial(_p) def this(other: GFPolynomial){ this(other.p.polynomial, bits) } override def self: GFPolynomial = this override def +(other: GFPolynomial): GFPolynomial = { GFPolynomial(this.p.polynomial ^ other.p.polynomial, bits) } override def -(other: GFPolynomial): GFPolynomial = { // In this case add and subtract are the same this + other } override def *(other: GFPolynomial): GFPolynomial = { val result: Polynomial = this.p mul other.p if (result.order >= bits){ GFPolynomial((result div modulo)._2, bits) } else GFPolynomial(result.polynomial, bits) } override def mulInverse: GFPolynomial = { if (p.polynomial == 0) throw new NoSuchElementException("Error: there is no multiplicative inverse for zero") var r1: Polynomial = Polynomial(modulo.polynomial) var r2: Polynomial = this.p var s1 = Polynomial(1) var s2 = Polynomial(0) var t1 = Polynomial(0) var t2 = Polynomial(1) var t = Polynomial(0) var s = Polynomial(0) var r = Polynomial(0) while(r2.polynomial > 0){ val q: Polynomial = Polynomial((r1 div r2)._1) r = r1 sub (q mul r2) r1 = r2; r2 = r s = s1 sub (q mul s2); s1 = s2; s2 = s t = t1 sub (q mul t2); t1 = t2; t2 = t } GFPolynomial(t1.polynomial, bits) } } }
Результат умножения может «вылезти» за рамки поля, поэтому иногда надо делить результат на модуль поля. Заметьте как реализовано деление, оно есть умножение a на мультипликативную инверсию b.
В свою очередь инверсия находится с помощью деления, определенного в классе Polynomial.
Вывод
Получилась самодельная реализация полей Галуа, которая в дальнейшем может быть улучшена путем увеличения возможного размера поля (вместо Int использовать длинную арифметику или что то в этом роде).
Данная статья может быть полезен студентам и всем кому интересна тема абстрактной алгебры, полей и теории кодирования.
Полный код приложения можно найти на github'е.
Комментарии (6)
kmu1990
07.01.2017 20:21А почему достаточно проврять только полиномы степени d/2? Разве полином степени d, не может получиться другим образом? Например, возьмем два неприводимых полинома степени 2 и 4, получим полином степени 6. Не должны ли мы проверять полиномы степени d/2 и меньше?

mathsatan
08.01.2017 17:11Полиномы d/2 и меньшие, проверяются рекурсивно, пока не дойдет до d=1
kmu1990
08.01.2017 17:17+1Вы не поняли вопрос, когда вы проверяете полином степени d, вы делите его только на полиномы в списке list, а он содержит только полиномы степени d/2, вопрос почему вы не проверяете делимость на полиномы других степеней, меньших d/2?

mathsatan
11.01.2017 03:56Вы правы, спасибо что заметили!
Исправил метод calcIrreducible(...), как Вы и сказали, полином должен проверяться не только на деление на неприводимые полиномы порядка d/2, но и на неприводмые полиномы порядка d/4, d/8 и т.д.kmu1990
11.01.2017 23:07И опять мне кажется, что вы не правы. Возьмем пример, который я приводил выше: два неприводимых полинома степени 2 и 4, в произведении дадут полином степени 6. Запустим ваш алгоритм для степени 6 — он вызовет генерацию неприводимых полиномов степени 3, которая рекурсивно вызовет генерацию неприводимых полиномов степени 1. Итого, у вас в списке окажутся неприводимые полиномы степени 1 и 3, но полинома степени 2 там не будет. Соответственно, делителя для произведения двух исходных полиномов там тоже не будет.


oisee
И всё-таки спеллчекер избавил бы от "деопозона".