Меня зовут Аят, я Android-инженер команды антифрода в inDrive. Эта статья не связана с продукционной разработкой, но будет касаться программирования. Я расскажу о Dynamic Programming (DP) и о том, как эффективно использовать предыдущий computation-опыт. Надеюсь, будет интересно. 

Введение в Dynamic Programming

Термин Dynamic Programming впервые использовал известный американский математик, один из ведущих специалистов в области вычислительной техники Ричард Беллман в 40-х годах XX века. Он писал, что Dynamic Programming — это способ решения сложных задач путем разбиения их на более мелкие подзадачи. 

Область решаемых проблем для DP должна соответствовать двум свойствам:

1. Оптимальная подструктура. В динамическом программировании означает, что решение подзадач меньшего размера может быть использовано для решения исходной задачи. Оптимальная подструктура — основное свойство задач парадигмы «разделяй и властвуй» (Divide and Conquer).

Классическим примером реализации является алгоритм сортировки слиянием (merge sort), в котором мы рекурсивно разбиваем задачи, спускаясь до самых простейших (массивы размером 1), после чего производим вычисление по каждому. Результаты используются для решения следующего вышестоящего слоя до тех пор, пока не будет достигнут исходный.

2. Перекрывающиеся подзадачи. Представляют набор операций, который выполняется многократно для получения искомого результата. В программировании — выполнение одного и того же кода с одними и теми же входными данными и одинаковыми результатами. Классический пример такой проблемы — вычисление N-го элемента в последовательности чисел Фибоначчи, который рассмотрим ниже.

Можно сделать вывод, что DP является частным случаем использования парадигмы Divide and Conquer или её более комплексной версией. Паттерн хорошо подходит для решения задач, связанными с комбинаторикой, где вычисляется большое количество разных комбинаций, но зачастую монотонно и одинаково для N-го количества элементов.

В проблемах с оптимальной подструктурой и перекрывающимися подзадачами при brute force-подходе мы имеем множественные повторяющиеся вычисления и операции. DP помогает оптимизировать решение и избежать дублирование computation двумя основными подходами: мемоизацией и табуляцией:

1. Мемоизация (нисходящее DP) реализуется через рекурсию. Задача разбивается на более мелкие подзадачи, их результаты записываются в память и комбинируются для решения исходной задачи путем повторного использования.

• Минус: подход расходует память стека рекурсивными вызовами функций и инициализацией расходных переменных внутри каждой.

• Плюс: гибкость к задачам DP.

2. Табуляция (восходящее DP) реализуется через итеративный метод. Подзадачи от самой малой до исходной вычисляются последовательно, итеративно.

• Минус: ограниченный спектр применения. Для подхода необходимо изначальное понимание всей последовательности подзадач. Но в некоторых проблемах это недостижимо.

• Плюс: эффективное использование памяти, так как все выполняется в рамках одной функции.

Теория может показаться скучной и непонятной — давайте разбирать примеры.

Problem: Fibonacci Sequence 

Классическим примером DP является вычисление N-го элемента в последовательности чисел Фибоначчи, когда каждый элемент является суммой двух предыдущих, а первый и второй элемент равен 0 и 1.

По условию сразу обратим внимание на свойство оптимальной подструктуры, так как для вычисления одного значения нужно получить предшествующее ему. Чтобы вычислить предыдущее, нужно получить те, который были ещё раньше и так далее. Свойство перекрывающихся подзадач подсвечу в разборе ниже.

Разберем на этой задаче три кейса:

1. Решение в лоб: выявим минусы подхода.

2. Оптимизированное решение с использованием мемоизации.

3. Оптимизированное решение с использованием табуляции. 

Решение в лоб (Straightforward/bruteForce approach)

Первое, что может прийти в голову — расписать рекурсию, суммировать предыдущие два элемента и выдать их результат.

/**
 * Straightforward(Brute force) approach
 */
fun fibBruteForce(n: Int): Int {
    return when (n) {
        1 -> 0
        2 -> 1
        else -> fibBruteForce(n - 1) + fibBruteForce(n - 2)
    }
}

На скрине ниже можно увидеть стек вызовов функций, чтобы вычислить пятый элемент в последовательности. 

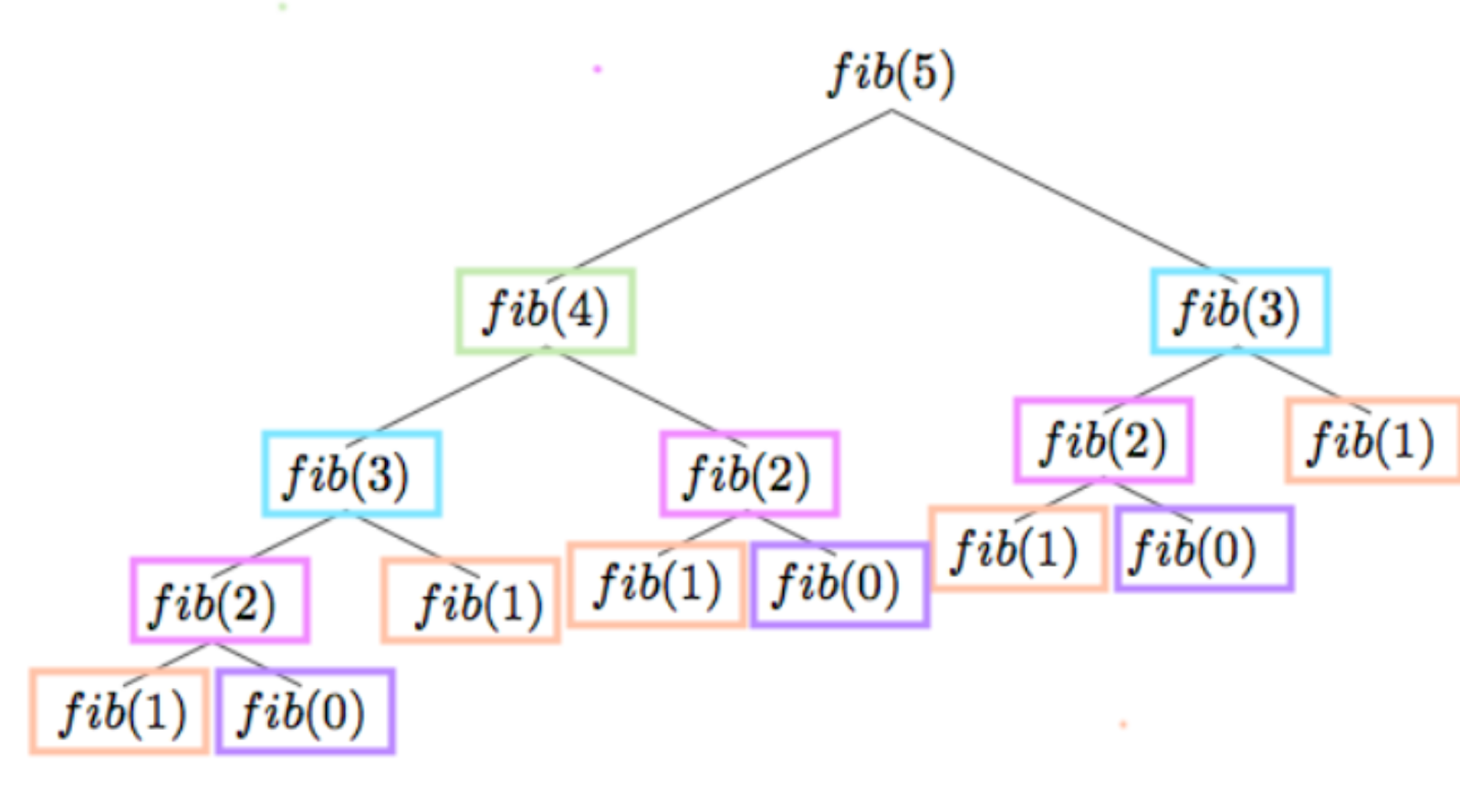
Обратим внимание, что функция fib(1) вызывается пять раз, fib(2) — три раза. Функции с одной сигнатурой, с одними и теми же параметрами запускаются повторно, делают одно и то же. С увеличением числа N дерево будет увеличиваться не линейно, а экспоненциально, что приведёт к колоссальному дублированию вычислений.

Math Analysis:
Time Complexity: O(2ⁿ),
Space Complexity: O(n) -> пропорционально максимальной глубине рекурсивного дерева, так как это максимальное количество элементов, которое может присутствовать в стеке неявных вызовов функций.

Итог: подход является чудовищно неэффективным. Например, для вычисления 30-го элемента потребуется 1073741824 операций.

Мемоизация (нисходящее DP) 

В этом подходе имплементация не будет сильно отличаться от предшествующего решения «грубой силы». За исключением того, что мы выделим дополнительную память, переменную memo, в которую будем записывать результат вычислений любой завершенной функции fib() в нашем стеке. 

Стоит отметить, что можно было обойтись массивом целых чисел и по индексам обращаться к нему, но для концептуальной наглядности была создана хеш-таблица.

/**
 * Memoization(Top-down) approach
 */
val memo = HashMap<Int, Int>().apply {
    this[1] = 0
    this[2] = 1
}

fun fibMemo(n: Int): Int {
    if (!memo.containsKey(n)) {
        val result = fibMemo(n - 1) + fibMemo(n - 2)
        memo[n] = result
    }
    return memo[n]!!
}

Снова обратим внимание на стек вызовов функций:

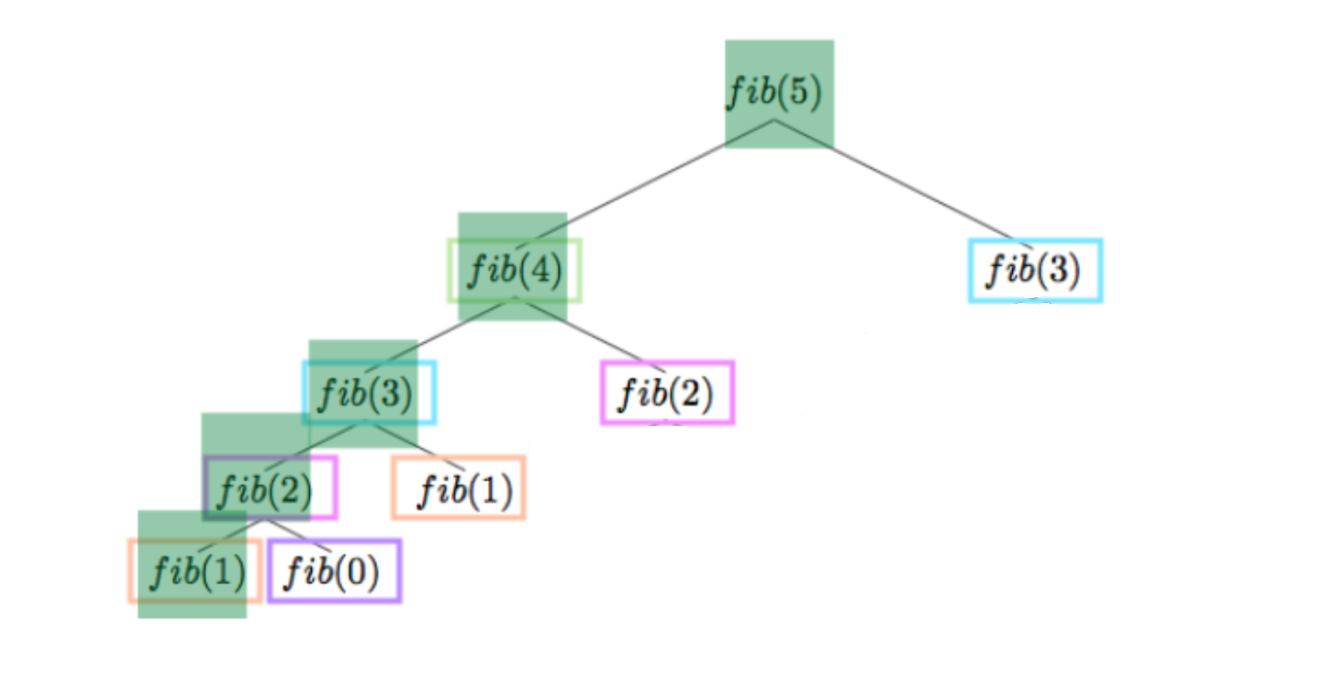
1. Первая выполненная функция, которая запишет результат в memo — highlighted fib(2). Она вернёт управление highlighted fib(3).

2. highlighted fib(3) получит своё значение, просуммировав результаты вызовов fib(2) и fib(1), запишет своё решение в memo и вернёт управление fib(4).

3. Наступает этап переиспользования раннего опыта — при возвращении управления fib(4) в ней ждёт своей очереди вызов fib(2). В свою очередь fib(2) вместо того, чтобы вызвать (fib(1) + fib(0)) воспользуется готовым решением из memo и сразу его вернёт.

4. fib(4) вычисляется и возвращает управление fib(5), которой осталось запустить fib(3). По прошлой аналогии fib(3) сразу вернёт значение из memo без вычислений.

Можем наблюдать сокращение количества вызовов функций и вычислений. Также с увеличением N сокращений будет экспоненциально кратно меньше.

Math Analysis:
Time Complexity: O(n)
Space Complexity: O(n)

Итог: разница в асимптотической сложности очевидна. Данный подход сократил её в сравнении с примитивным решением до линейной во времени и не увеличил в памяти.

Табуляция (восходящее DP)

Как упоминалось выше, в этом подходе итеративно идёт вычисление от меньшей подзадачи к большей . В случае с Фибоначчи наименьшие «подзадачи» — это первый и второй элемент в последовательности, 0 и 1 соотвественно.

Нам четко известна зависимость элементов относительно друг друга, которая выражена в формуле: fib(n) = fib(n-1) + fib(n-2). Зная предыдущие элементы, мы без труда можем подсчитать следущий, идущий после него и так далее.

Суммируя известные нам значения, получаем следующий элемент. Проводим эту операцию циклично до получения искомого.

/**
 * Tabulation(Bottom-up) approach
 */
fun fibTab(n: Int): Int {
    var element = 0
    var nextElement = 1
    for (i in 2 until n) {
        val newNext = element + nextElement
        element = nextElement
        nextElement = newNext
    }
    return nextElement
}

Math Analysis:
Time Complexity: O(n)
Space Complexity: O(1)

Итог: подход также эффективен с точки зрения скорости как и мемоизация, но при этом расходует константное количество памяти.

Problem: Unique Binary Trees

Рассмотрим более комплексную задачу: необходимо найти количество всех структурно уникальных бинарных деревьев, которые можно построить из N нод.

Бинарное дерево — иерархическая структура данных, в которой каждая нода имеет не более двух потомков. Как правило, первый называется родительской нодой, а дети — левым и правым наследниками.

Предположим, нам нужно найти решения для N = 3. Структурно уникальных деревьев для трех нод — 5. Их можно просчитать в голове, но при увеличении N эскалация вариаций будет огромной и визуализировать их в голове будет невозможно.

Данную задачу можно отнести к комбинаторике. Давайте разбираться, какие комбинации можно построить и как выявить паттерн их построения.

1. Каждое дерево начинается с вершинной ноды (Vertex of The Tree). Начиная с неё, оно разрастается вглубь.

2. Каждая нода является началом нового дочернего дерева (subtree), как указано на скрине. Левое дочернее дерево окрашено в зелёный цвет, правое — в красный. У каждой из них своя вершина.

Рассмотрим пример задачи, где N = 6 на концептуальном уровне. Назовём нашу функцию вычисления numOfUniqueTrees(n: Int).

В нашем примере дано 6 нод, из которых по ранее указанному принципу одна нода расходуется на вершину дерева, остаток — 5 нод.

Далее мы взаимодействуем с оставшимися нодами. Делать это можно по-разному. Например, все пять нод использовать для построения левого поддерева или же все пять отправить для правого. Или разбить ноды по обоим одновременно — влево 2 и вправо 3 (см. скрин ниже), таких вариаций у нас ограниченное множество.

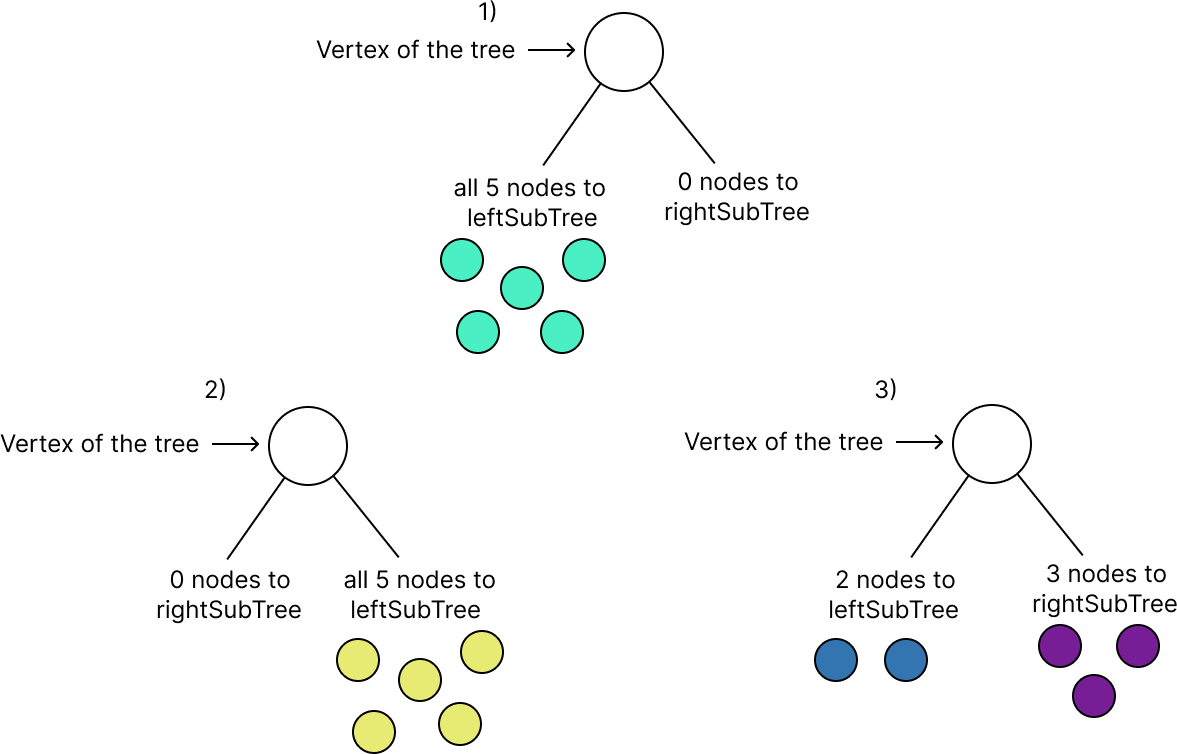
Чтобы получить результат numOfUniqueTrees(6), нужно перебрать все вариации распределений наших нод. Они указаны в таблице:

В таблице 6 разных распределений нод. Если мы найдём, сколько уникальных деревьев можно сгенерировать для каждого распределения и просуммируем их, получим наш итоговый результат.

Как найти количество уникальных деревьев для распределения? У нас два параметра: leftNodes, rightNodes (левый и правый столбец в таблице). Количество будет равно numOfUniqueTrees(leftNodes) * numOfUniqueTrees(rightNodes).

Почему? Слева у нас будет X уникальных деревьев и на каждое мы можем подставить Y уникальных вариаций деревьев справа. Перемножаем и получаем результат.

Найдем вариации для первого распределения (5 left, 0 right). numOfUniqueTrees(5) * numOfUniqueTrees(0), так как справа у нас нет нод. Результат сводится к numOfUniqueTrees(5) — количеству уникальных поддеревьев слева с неизменной правой стороной.

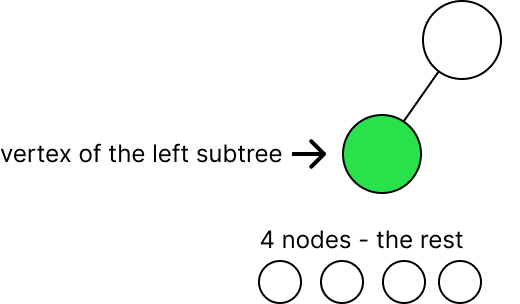
Подсчёт numOfUniqueTrees(5). Теперь у нас меньшая подзадача, оперировать с ней мы будем также, как и с большей. На этом этапе нам очевидна черта задач DP — оптимальная подструктура, рекурсивное поведение.

Одна нода (green node) отправляется на вершину. Остаток (четыре ноды) распределяем аналогично прошлому опыту (4:0), (3:1), (2:2), (1:3), (0:4). Вычислим первое распределение (4:0). Оно равно numOfUniqueTrees(4) * numOfUniqueTrees(0) -> numOfUniqueTrees(4) по ранней аналогии.

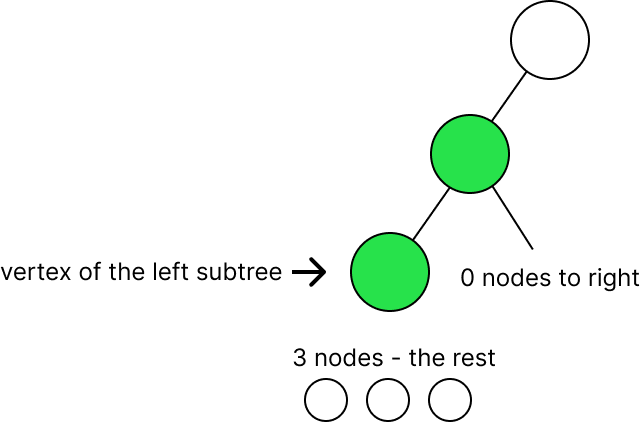
Подсчёт numOfUniqueTrees(4). Выделяем ноду на вершину, и у нас остается 3.
Распределения (3:0), (2:1), (1:2), (0:3).

Для двух нод всего 2 вариации, для одной — одна. По скрину в начале разбора задачи мы знаем, что для трёх нод есть 5 вариаций.

Как результат — распределения
(3:0), (0:3) будут равны 5, (2:1), (1:2) — 2. Суммируем 5 + 2 + 2 + 5, получаем 14. numOfUniqueTrees(4) = 14.

Записываем результат вычисления в переменную memo по опыту мемоизации. Каждый раз, когда нам понадобится получить вариации для четырёх нод, мы не будет их высчитывать снова, а переиспользуем ранний опыт.

Возвращаемся к подсчету (5:0), который равен сумме распределений (4:0), (3:1), (2:2), (1:3), (0:4). Известно, что (4:0) = 14. Обращаемся к memo, (3:1) = 5, (2:2) = 4 (2 вариации слева * 2 справа), (1:3) = 5, (0:4) = 14. Суммируем и получаем 42, numOfUniqueTrees(5) = 42.

Возвращаемся к подсчёту numOfUniqueTrees(6), которая равна сумме распределений
(5:0) = 42, (4:1) = 14, (3:2) =10 (5 left * 2 right), (2:3) = 10, (1:4) = 14, (0:5) = 42. Суммируем и получаем 132, numOfUniqueTrees(5) = 132.

Задача решена!

Итог: отметим перекрывающиеся подзадачи в решении при N = 6. При решении в лоб numOfUniqueTrees(3) вызывался бы 18 раз (скрин ниже), с увеличением N повторений будет гораздо больше.

Подсвечу, что количество уникальных деревьев для (5 left, 0 right) и (0 left, 5 right) будет одинаковым. Только в одном случае они будут слева, а во втором случае справа. Это работает и для (4 left, 1 right) и (1 left, 4 right).

Мемоизация как подход динамического программирования позволил нам оптимизировать решение такой комплексной задачи.

Имплементация

class Solution {
    fun numTrees(n: Int): Int {
        val memo = arrayOfNulls<Int>(n+1)
        return calculateTees(n, memo)
    }

    fun calculateTees(n: Int, memo:Array<Int?>): Int {
        var treesNum = 0
        if(n < 1) return 0
        if(n == 2) return 2
        if(n == 1) return 1
        if(memo[n]!=null)
            return memo[n]!!

        for (i in 1..n){
            val leftSubTrees = calculateTees( i - 1, memo)
            val rightSubTrees = calculateTees(n - i, memo)

            treesNum += if(leftSubTrees>0 && rightSubTrees>0){
                leftSubTrees*rightSubTrees
            } else
                leftSubTrees+leftSubTrees
        }
        memo[n] = treesNum
        return treesNum
    }
}

Вывод

При определенных обстоятельствах решения задач с помощью Dynamic Programming может сэкономить огромное количество времени и сделать алгоритм максимально эффективным.

Спасибо, что дочитали статью до конца. Если у вас есть вопросы, буду рад ответить на них в комментариях