Другими словами мы имеем частный случай задачи по раскрою материала.
Немного предыстории: в одном из своих проектов у меня появилась задача по расчету необходимого количества листов металла для производства деталей круглой формы. В моем случае это листы металла стандартного габарита 6000x1500 миллиметров.
Поискав готовые решения этой задачи, я решил написать свой вариант.
Не судите строго это все родилось за несколько часов :)
Постановка задачи
Найти наименьшее количество листов металла, заданного габарита для производства заданного списка деталей круглой формы, заданных своими диаметрами.
Описание алгоритма
Из полученного на входе словаря, содержащего радиусы кругов и их количества мы формируем массив, вида:
# Словарь на входе от пользователя
user_circles = {
830 : 1,
730 : 2,
490 : 4,
360 : 6,
280 : 8,
150 : 12,
100 : 16,
50 : 18,
}
# Массив упорядоченных по убыванию радиуса объектов-кругов
self.circles = [
Circle(830),
Circle(730),
Circle(730),
Circle(490),
Circle(490),
Circle(490),
Circle(490),
...
]Далее мы создаем новый лист (прямоугольник) заданных пользователем размеров:
self.sheets.append(Sheet(self.sheet_w, self.sheet_h))Организуем цикл по массиву с упорядоченными объектами-кругами и для каждого круга используем метод поиска наилучшей координаты Y:
for i in self.circles:
i.cx, i.cy = self.find_best_packing_start_point(current_sheet, i)Вот небольшая иллюстрация этого алгоритма:
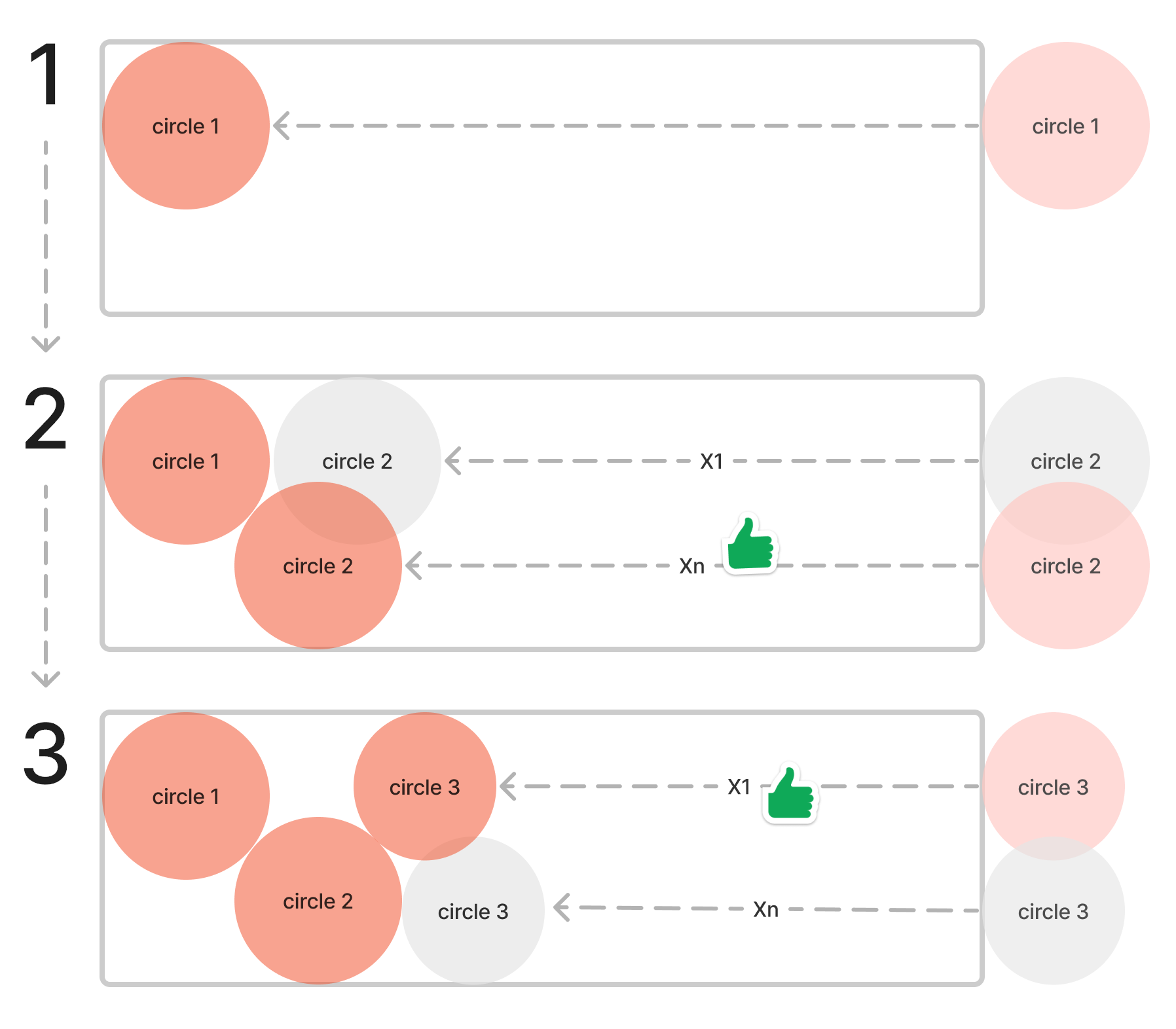
Если очередной круг был успешно помещен на текущий лист (прямоугольник) то из словаря кругов, заданного пользователей вычитается круг данного радиуса:
self.user_circles[i.r] -= 1Если текущий круг не входит в лист (прямоугольник) по габаритам, то он добавляется в переменную:
self.circles_excluded[i.r] += 1Когда для текущего листа (прямоугольника) мы попробовали разместить все круги из массива self.circles мы генерируем заново массив self.circles из оставшихся для размещения кругов:
# Убираем круги, которые уже размещены
def clean_circles(self):
circles_cleaned = []
for i in self.user_circles.keys():
for k in range(self.user_circles[i]):
circles_cleaned.append(Circle(i))
self.circles = circles_cleanedДалее мы добавляем следующий лист и повторяем алгоритм пока не останется кругов для размещения.
Исходный код на Python
import svgwrite
import math
class Sheet:
def __init__(self, w, h):
self.w = w
self.h = h
self.circles = []
class Circle:
def __init__(self, r, cx=None, cy=None):
self.cx = cx
self.cy = cy
self.r = r
@staticmethod
def two_circle_intersections(c1, c2):
x0, y0, r0 = c1.cx, c1.cy, c1.r
x1, y1, r1 = c2.cx, c2.cy, c2.r
d = math.sqrt((x1-x0)**2 + (y1-y0)**2)
if d > r0 + r1 :
return False
if d < abs(r0-r1):
return False
if d == 0 and r0 == r1:
return False
else:
return True
class CirclePacking:
ACCURACY = 20 # На сколько частей делим высоту для поиска наилучшей позиции по вертикали для текущего круга
def __init__(self, sheet_w, sheet_h, circles, cut_border):
self.sheet_w = sheet_w
self.sheet_h = sheet_h
self.user_circles = circles
self.circles = []
self.sheets = []
self.circles_excluded = {}
self.cut_border = cut_border
def create_circles_sorted(self):
self.circles = []
for i in reversed(sorted(self.user_circles.keys())):
for k in range(self.user_circles[i]):
self.circles.append(Circle(i))
# Убираем круги, которые уже размещены
def clean_circles(self):
circles_cleaned = []
for i in self.user_circles.keys():
for k in range(self.user_circles[i]):
circles_cleaned.append(Circle(i))
self.circles = circles_cleaned
def packing(self):
self.create_circles_sorted()
while sum(self.user_circles.values()) > 0:
#print(self.user_circles, self.circles)
self.sheets.append(Sheet(self.sheet_w, self.sheet_h))
current_sheet = self.sheets[-1]
for i in self.circles:
i.cx, i.cy = self.find_best_packing_start_point(current_sheet, i)
if i.cx is None and i.cy is None:
if i.r not in self.circles_excluded:
self.circles_excluded[i.r] = 1
else:
self.circles_excluded[i.r] += 1
self.user_circles[i.r] -= 1
else:
# Проверка что мы не вышли за длину листа
if i.cx > current_sheet.w - i.r - self.cut_border:
pass
else:
self.user_circles[i.r] -= 1
current_sheet.circles.append(i)
self.clean_circles()
# Ищем наилучшую позицию по вертикали для размещения круга
def find_best_packing_start_point(self, s, c):
try_results = {}
N = CirclePacking.ACCURACY
step = int((s.h -c.r) / N)
# Формируем массив координат по вертикали для попыток
try_y = [c.r, s.h-c.r, s.h/2]
for i in range(int((s.h - c.r) / step)):
try_y.append(c.r + step * i)
# Пробуем все координаты из массива попыток
for i in try_y:
c.cx = s.w + c.r
c.cy = i
self.move_circle(s, c)
# Проверяем что мы вошли на лист
if c.cy >= c.r + self.cut_border and c.cy <= s.h - c.r - self.cut_border:
try_results[c.cx] = c.cy
if try_results == {}:
cx = cy = None
else:
cx = sorted(try_results.keys())[0]
cy = try_results[cx]
return cx, cy
def move_circle(self, s, c):
while c.cx > c.r + self.cut_border:
if self.check_intersections(s, c):
return
c.cx -= 1
def check_intersections(self, s, c):
for i in s.circles:
i.r += self.cut_border
if Circle.two_circle_intersections(i, c):
i.r -= self.cut_border
return True
i.r -= self.cut_border
return False
def draw_sheet_with_circles(self, sheet_idx, scale, filename):
sheet = self.sheets[sheet_idx]
w = sheet.w * scale
h = sheet.h * scale
border_x = 150 * scale
border_y = 150 * scale
svg = svgwrite.Drawing(filename = filename, size = (str(w+border_x*2)+'px', str(h+border_y*2)+'px'))
svg.add(svg.line(stroke='red', start=(str(0+border_x)+'px', str(0+border_y)+'px'), end=(str(w+border_x)+'px', str(0+border_y)+'px')))
svg.add(svg.line(stroke='red', start=(str(0+border_x)+'px', str(0+border_y)+'px'), end=(str(0+border_x)+'px', str(h+border_y)+'px')))
svg.add(svg.line(stroke='red', start=(str(0+border_x)+'px', str(h+border_y)+'px'), end=(str(w+border_x)+'px', str(h+border_y)+'px')))
line1 = svg.add(svg.line(stroke='red', start=(str(w+border_x)+'px', str(0+border_y)+'px'), end=(str(w+border_x)+'px', str(h+border_y)+'px')))
line1.dasharray([5, 10])
for i in sheet.circles:
cx = i.cx * scale
cy = i.cy * scale
r = i.r * scale
svg.add(svg.circle(center=(str(cx+border_x)+'px', str(cy+border_x)+'px'), r=str(r)+'px', stroke='black', fill='white', stroke_width=1))
svg.save()Пример работы алгоритма
Ниже приведен пример работы алгоритма:
circles = {
830 : 1,
730 : 2,
490 : 4,
360 : 6,
280 : 8,
150 : 12,
100 : 16,
50 : 18,
}
cp = CirclePacking(sheet_w=6000, sheet_h=1500, circles=circles, cut_border=20)
cp.packing()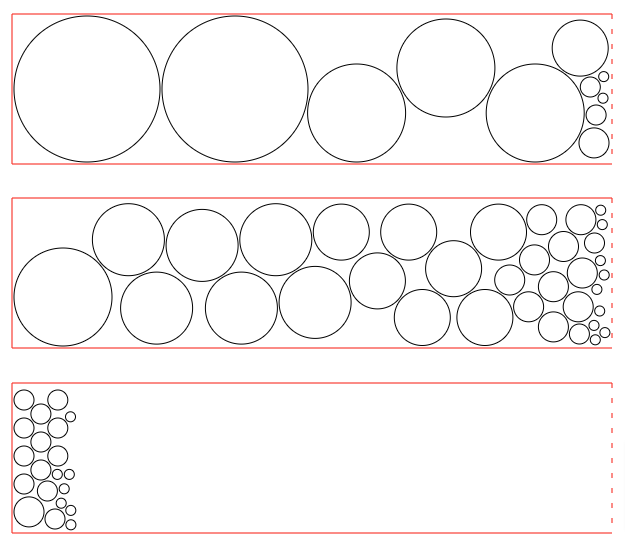
Обратите внимание на то, что круг с радиусом 830 не вошел на листы 6000x1500 и он помещен в атрибут: cp.circles_excluded:
cp.circles_excluded
# {830: 1}Оставшиеся вопросы:
Как ускорить работу алгоритма не выходя за возможности стандартного Python (не использовать библиотеки ускорения кода Python)?
Как еще повысить плотность заполнения листов?
Ссылки
Github: https://github.com/tau15/python_circle_packing_in_rectangle
Google Colab: https://colab.research.google.com/drive/1e-RoNHStyqdyROZNPHga_vvrIKyRy3ZR?usp=sharing
Вопросы и предложения на алгоритму пишите мне: @TAU15
Комментарии (10)

SnakeSolid
00.00.0000 00:00+3При "установке" очередного круга рассчитывать заполнители (как в диаграммах Вороного). Потом из пула "свободных" кругов сначала подбирать круги максимально вписывающиеся в заполнители. Если ничего подобрать не получилось - размещаем самый большой доступный круг в конец листа. При "установке" в заполнитель если новый круг при пересекает один или несколько заполнителей - удаляем все пересечения и пересчитываем заполнители для установленного круга. Самое сложное будет - найти места для заполнителей.
Попытался нарисовать как это должно работать
Синие - это места-заполнители, красная стрелка - добавленный круг.
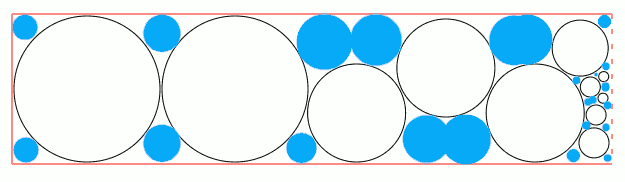
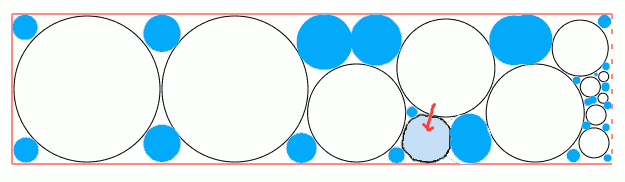

Dimon41
00.00.0000 00:00+13й лист явно лишний. Я бы попробовал сротировать через один. Сначала самый большой потом самый маленький. Как колоду карт.

zartdinov
00.00.0000 00:00+2Нет смысла искать логичное решение, это стандартная NP-полная задача о рюкзаке.




deemytch
Отсортировать круги по размеру и брать с двух концов сразу? В примере весь третий лист мог бы войти в два предыдущих.
alnite
Вот кстати да, вы хорошо сформулировали "претензию" к алгоритму, что слишком много пустот остаётся на листе. Плюс, если это для раскроя, то совсем не обрабатывается уменьшение холостого хода раскроечной головки (что там, лазер, или плазма или другое).
Плюс, если на ртсунках реальный результат алгоритма, то видно, что много кругов "посажены" не вкрай, а значит, теряется расстояние по длине.
Artur_Averin
Я бы сделал иначе - мы в угол листа выставляем первый, самый большой круг, и в полученный уголок страницы мы вписываем наиболее большой подходящий в него круг по размеру
Biga
Мне опыт подсказывает, что отсортировано правильно, но каждый следующий круг надо класть не вверх, а искать место по всему листу как можно ниже (левее?). То есть сначала идут большие круги, и как только дело дойдёт до круга, который поместится в уголок, туда его и помещать. Ниже уже написали, как выбрать наилучшее место на листе из всех возможных.