В данной статье будет рассмотрена небольшая модификация алгоритма градиентного спуска, в миллионы раз менее подверженная застреванию в локальном оптимуме, чем существующие (и с возможностью распараллеливания).
Данную статью побудило написать качество современных публикаций на тему проблем современного машинного обучения (https://habr.com/ru/company/skillfactory/blog/717360/ Wouter van Heeswijk, PhD).
Что в этом не так?
Неудовлетворительные обновления градиента политики. Например, очень малые шаги, когда зависают в локальном оптимуме, или большие шаги, из-за которых упускают наибольшее вознаграждение.
В любой формулировке мы или исследуем все пространство малыми шагами (и не пропускаем оптимум), или приходим к оптимуму большими шагами. Вообще правильнее было бы настраивать размер шагов исходя из какого-либо анализа функции ошибки с использованием БПФ, но это в следующей статье.
Алгоритмы, основанные на аппроксимации функции полезности, систематически выбирают действия с завышенной полезностью.
Залог оптимальности эвристики в отсутствии занижения функции полезности. В случае попытки сэкономить миллион\миллиард шагов алгоритма можно получить субоптимальные эвристики и не получить решение и за триллион.
Так же следует помнить, что градиентный спуск не является оптимальной эвристикой для всех типов функций ошибки (поэтому придумали обучения с моментом, и прочие трюки, которые на первый взгляд помогают быстрее находить оптимальные решения). Однако лишаться оптимальности пусть даже в некотором подмножестве множества параметров смысла нет.
Что делать(с градиентным спуском)?
Давайте напишем свою версию градиентного спуска, с множеством начальных точек и очередью с приоритетом.
В общем алгоритм выглядит так:
-
Инициализируем N начальных точек, для каждой из точек считаем ошибку, записываем все в очередь с приоритетом (можно делать и параллельно)
Цикл:
Достаем точку из очереди, считаем градиент ошибки, считаем изменение положения, считаем ошибку
Если точка застряла в локальном оптимуме (последние trace_len положений отличаются менее чем на эпсилон) - добавляем точку в список застрявших в локальном оптимуме, инициализируем новую точку
Если нет - помещаем точку обратно в очередь с приоритетом
-
Раз в несколько шагов обновляем очередь с приоритетом (можно делать и параллельно), чтобы уменьшить среднюю ошибку и увеличить оптимальность поиска.
Просто добавляем некоторое количество точек в очередь. Удаляем такое же количество точек с максимальной ошибкой.
Повторяем п. 2-5 пока не закончатся шаги или не получим требуемый уровень ошибки
Что нам это даст?
Не требует доказательств, что шанс застрять в локальном оптимуме равен примерно
, где N - количество начальных точек, P - шанс застрять в локальном оптимуме при единичном запуске
Сложность (количество шагов, требуемое для решения) будет меньше, чем N градиентных спусков (по M шагов), или M*N, но больше M+N(инициализация и спуск).
Код
python
from queue import PriorityQueue
import numpy as np
import random
from math import sqrt
##Parameters
#learning rate
dt = 0.1
#maximum step count
maxSteps = 20000
#minimum_error
minError = 0.01
##Specifical parameters
#small number to calculate derivative of target function (for using script with large object functions, like neural nets or so)
delta = 0.1
#trace length, in points
trace_len = 10
#initilal point count
N = 10000
#size of parameters space
spaceSize=[[-100,100],[-100,100]]
#for analysis purpose
GetErrorCallCount = 0
localOptimums = []
#taked from https://github.com/behnamasadi/gradient_descent/
def objective_function(vector):
z = -(4*np.exp(-(vector[0]-4)**2 - (vector[1]-4)**2)+2*np.exp(-(vector[0]-2)**2 - (vector[1]-2)**2))+4+0.2*np.sin(vector[0])+0.2*np.cos(vector[1])
return z
#we will compute exact derivative
def get_objective_function_derivatives(vector,delta,error):
res = []
initial_error = error
pos_vector = vector[0]
for n in range(len(pos_vector)):
vec = pos_vector
vec[n] = vec[n]+delta
derivative_n = -(GetError(vec)-initial_error)/delta
res.append(derivative_n)
#change to correct derivative calculation
return res
#returns normalized derivative vector
def get_error_gradient(vector,delta, error):
derivative = get_objective_function_derivatives(vector, delta, error)
#recalculate derivative, if take 0 multiply delta by ten
while all(d ==0 for d in derivative):
# print("get zero derivative")
# print(derivative)
# print(delta)
delta=delta*10
#doesnt help, return ReInitialization flag
if (delta>1000):
return [True, derivative]
derivative = get_objective_function_derivatives(vector, delta, error)
return [False, derivative]
def initGradDesc(sampleVector, priorityQueue, N):
res = []
global spaceSize
#Let's generate N random vectors with same length
for num in range(N):
#Initialize derivatives and vector randomly
pos = []
for i in range(len(sampleVector)):
pos.append(random.uniform(spaceSize[i][0],spaceSize[i][1]))
error = GetError(pos)
res.append([error, [pos]])
#Now we have N random vectors, please note that we must have normaziled data everywhere )
#lets add all those vectors in priorityQueue with our GetError Function
for x in res:
priorityQueue.put(x)
#TODO: rewrite euler integration and calculation of derivatives
#use simpliest Euler method to find change of coordinates with some derivatives
def calculateNewPosition(stateVector, error_grad, errorInit):
delta = []
#and, some trick again, trying to normalize error
delta = [x[0]+x[1]*dt for x in zip(stateVector[0],error_grad)]
return delta
#returns error for current vector as a solution
def GetError(vector):
#update call count
global GetErrorCallCount
GetErrorCallCount = GetErrorCallCount+1;
return objective_function(vector)
def getLengthBetween(item, newPoint):
l = sqrt(sum((i[0]-i[1])*(i[0]-i[1]) for i in zip(item,newPoint)))
return l
def makeGradDesc(priorityQ, point, withDetection):
global delta
errorInit = point[0]
state_vector = point[1]
#Note that point structure is [vec, derivatives_1,...,derivatives_N]
error_grads = get_error_gradient(state_vector,delta,errorInit)
error_grad = error_grads[1]
newPoint = calculateNewPosition(state_vector, error_grad, errorInit)
error = GetError(newPoint)
#merge data into one list
res = [newPoint]
curr_trace = 0;
for positions in state_vector:
res.append(positions)
curr_trace = curr_trace+1
if (curr_trace>=trace_len):
break
#calculate error
res = [error,res]
#Check for local optimum (position and cost function dont change last N steps), or we get Zero derivative and still have a significant error, initialize new point
if (withDetection and((error_grads[0] and error>minError) or (all(getLengthBetween(item, newPoint) < dt for item in state_vector)))):
localOptimums.append(res)
initGradDesc(newPoint, priorityQ, 1)
else:
if (not(withDetection) and all(getLengthBetween(item, newPoint) < dt for item in state_vector)):
localOptimums.append(res)
initGradDesc(newPoint, priorityQ, 1)
else:
priorityQ.put(res)
#main gradient descent function that runs for MaxStepCount or while minimal error is not reached
def PreformDradDesc(priorityQ, MaxStepCount,minError, withDetection):
global GetErrorCallCount
point = priorityQ.get()
error = point[0]
steps = 0
while ((abs(error)>=abs(minError)) and (GetErrorCallCount<MaxStepCount)):
steps = steps + 1
makeGradDesc(priorityQ, point, withDetection)
point = priorityQ.get()
error = point[0]
return [steps, error, point]
Ne=100
res = []
ec1 = 0
for i in range(Ne):
GetErrorCallCount = 0
#Where to store statistics about steps count/result error
research_results = []
#Queue needed for our A*
priorityQ = PriorityQueue()
initGradDesc(spaceSize, priorityQ, N+1)
minimum_error = PreformDradDesc(priorityQ, maxSteps, minError, True)
res.append([GetErrorCallCount, minimum_error[1]<minError])
ec1 = ec1+ GetErrorCallCount
print(i)
print(ec1)
print(res)
s1 = sum(item[1] for item in res)
print(ec1/s1)
print(s1/Ne)
# Mean steps: 209502.76136363635
# global optimum: 0.88
# Mean steps: 379639.8307692308
# global optimum: 0.65
# 234927.15789473685
# 0.19
# 346809.0909090909
# 0.11
res2 = []
ec2 = 0
for i in range(Ne):
GetErrorCallCount = 0
#Where to store statistics about steps count/result error
research_results = []
#Queue needed for our A*
priorityQ = PriorityQueue()
initGradDesc(spaceSize, priorityQ, 1)
minimum_error = PreformDradDesc(priorityQ, maxSteps, minError, False)
res2.append([GetErrorCallCount, minimum_error[1]<minError])
ec2 = ec2+ GetErrorCallCount
print(i)
print(ec2)
print(res2)
s2 = sum(item[1] for item in res2)
print(ec2/s2)
print(s2/Ne)
#Print results
print("Cost function calls for initialization: ")
print(GetErrorCallCount)
minimum_error = PreformDradDesc(priorityQ, maxSteps, minError)
print("Minimum error: ")
print(minimum_error[1])
print("Result point: ")
print(minimum_error[2][1][1])
print("Initial points: ")
print(N)
print("Total steps: ")
print(minimum_error[0])
print("Maximum steps: ")
print(maxSteps)
print("Cost function calls: ")
print(GetErrorCallCount)
print("Local minimums queue len: ")
print(len(localOptimums))
# for item in localOptimums:
# print(item)
Самое интересное - Objective_function:
print(objective_function([10,10])==objective_function([100,100]))
TrueИли, функция имеющая нулевой градиент при 99.9925% значениях параметров.
Результаты анализа
Да, я специально взял "простейший пример", с нулевым градиентом. И потом добавил 360000 локальных минимумов :)
z = -(4*np.exp(-(vector[0]-4)**2 - (vector[1]-4)**2)+2*np.exp(-(vector[0]-2)**2 - (vector[1]-2)**2))+4+0.2*np.sin(vector[0])+0.2*np.cos(vector[1])
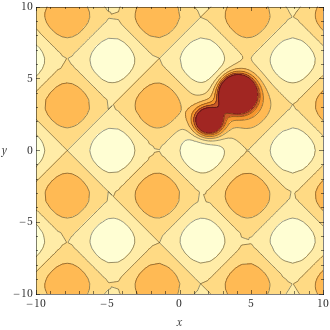
В 10 запусках из 10 был получен глобальный минимум (что уже само по себе неплохо :) ).
Детектор локальных минимумов работает как на локальный минимум, так и на плато.
Давайте запустим каждый из алгоритмов 100 раз и посмотрим, что произойдет.
Ну и сравнение простого градиентного спуска с перезапуском на плато с полным алгоритмом(я уменьшил число шагов\начальных точек до 10000 с 10 млн):
Диапазон входных параметров функции:
[[-100;100],[-100;100]]
Функция ошибки:
z = -(4*np.exp(-(vector[0]-4)**2 - (vector[1]-4)**2)+2*np.exp(-(vector[0]-2)**2 - (vector[1]-2)**2))+4+0.2*np.sin(vector[0])+0.2*np.cos(vector[1])Количество шагов: 20000
Количество начальных точек при инициализации: 10000
Полный список параметров
##Parameters
#learning rate
dt = 0.1
#maximum step count
maxSteps = 20000
#minimum_error
minError = 0.1
##Specifical parameters
#small number to calculate derivative of target function (for using script with large object functions, like neural nets or so)
delta = 0.1
#trace length, in points
trace_len = 10
#initilal point count
N = 10000
#size of parameters space
spaceSize=[[-100,100],[-100,100]]
#for analysis purpose
GetErrorCallCount = 0
Вызовов функции оценки |
Результатов в глобальном оптимуме |
Вызовов функции оценки на глобальный оптимум |
|
Полный алгоритм с обновлением очереди |
1217770 |
94% |
13236.63043 |
|
Полный алгоритм (лучше, чем SOTA по ссылкам ниже) |
1950076 |
80% |
24075.012345679013 |
|
Только перезапуск при плато/локальном минимуме (multistart с остановкой на плато\ в минимуме) |
1966037 |
45% |
43689.71111111111 |
|
Просто градиентный спуск (multistart без остановки в минимуме\на плато) |
2000100 |
0% |
Inf :) |
Невероятно, но простое использование очереди с приоритетом помогает добиться лучших результатов при поиске глобального оптимума при градиентном спуске.
Увы очереди с приоритетом и оптимальные эвристики не слишком часто используются разработчиками библиотек\алгоритмов связанных с поиском глобального минимума, и сравнить особо не с чем.
Но как же http://www.techmat.vgtu.lt/~art/proc/file/ZiliJu.pdf или https://aip.scitation.org/doi/pdf/10.1063/1.5089989?
Все просто, параллельный запуск N градиентных спусков даже с priority queue хуже,
чем последовательный запуск градиентного спуска, который хуже например,
последовательного запуска градиентного спуска с запуском N процессов, обновляющих данные в очереди с приоритетом, с целью понизить среднюю ошибку в последней.
Использованные материалы
Комментарии (15)

Flux
00.00.0000 00:00+7At first I was like:
модификация алгоритма градиентного спуска, в миллионы раз менее подверженная застреванию в локальном оптимуме, чем существующие
But then,
В 10 запусках из 10…
Не требует доказательств, что ...Похоже что вы таки решили проблему поиска глобального минимума и знатно подняли качество современных публикаций на тему проблем машинного обучения, это достойно уважения!
Рекомендую вам слать статью на NeurlIPS, дедлайн подачи в мае месяце.

Vaitek
00.00.0000 00:00Мб прогнать хотя бы на этом: https://pypi.org/project/OptimizationTestFunctions/ и сравнить с популярными решениями?

ValeriyPu Автор
00.00.0000 00:00Хабр увы не позволяет редактировать статьи.
Это сильное заявление
Очень сильное, учитывая что
print(objective_function([10,10])==objective_function([100,100])) TrueИли, функция имеющая нулевой градиент при 99.9925% значениях параметров :)
Да, я специально взял "простейший пример", с нулевым градиентом. И потом добавил 360000 локальных минимумов :)
Или примерно2000*2000*9/(10*10) = 40000*9=360000
локальных минимумов в диапазоне [[-1000;1000],[-1000;1000]]z = -(4*np.exp(-(vector[0]-4)**2 - (vector[1]-4)**2)+2*np.exp(-(vector[0]-2)**2 - (vector[1]-2)**2))+4+0.2*np.sin(vector[0])+0.2*np.cos(vector[1])Cost function calls for initialization: 1000001 Minimum error: -0.009953628971875753 Result point: [3.855589965005124, 4.428819432720052] Initial points: 1000000 Total steps: 6778543 Maximum steps: 100000000 Cost function calls: 28113741 Local minimums queue len: 6778111 Raw results:Как видим, у нас получилось гигантское количество локальных минимумов, но это не из-за ошибок в скрипте. Видимо, начальные точки по нескольку раз приводили в один и тот же локальный минимум
Даже с локальными минимумами 5 из 5 запусков окончились в Глобальном минимуме.
ну и ответы:
в 99.9925% обычный градиентный спуск не покажет вообще никаких результатов. (100 запусков из 100 закончились ничем, и я использовал в 20 раз больше вызовов ObjectiveFunction) (Плато или тысячи\миллионы локальных минимумов)
С функциями с большей размерностью будет то же самое, только в большем пространстве
Нейросети? Нет, зачем? Есть какая-то разница? ) Поменяются определения оптимальности? ) Градиентный спуск применяется не только в обучении нейронных сетей, но и для различных видов регрессии, и даже в системах машинного зрения
слишком сложный сарказм. Есть же PhD vacancies )
Да, добавление момента это здорово, но не оптимально.
К сожалению представленный бенчмарк гораздо проще, чем имеющаяся тестовая функция.
masai
00.00.0000 00:00К сожалению представленный бенчмарк гораздо проще, чем имеющаяся тестовая функция.
Не проще.

masai
00.00.0000 00:00+2в миллионы раз менее подверженная застреванию в локальном оптимуме, чем существующие
Держать в памяти миллион точек — не очень-то практично. Для сложных нейронных сетей и пара точек не всегда в памяти помещается. :)
Насколько я вижу, идея метода — это запуск градиентного спуска для разных начальных точек (то есть, это multistart optimization), а очередь нужна только для оптимизации вычислений.

masai
00.00.0000 00:00https://arxiv.org/abs/1401.3894 — вот, кстати, пример метода с multi-start, в котором есть множество алгоритмов локального поиска и делается выбор, каким искать.
Насчёт эвристики с выбором лучшего. Вот тут как раз не факт, что это как-то ускоряет поиск. Всё зависит от ландшафта функции. Может там всё усеяно седловыми точками. Тогда градиентный спуск будет всегда застревать и нужно взять что-то другое.

ValeriyPu Автор
00.00.0000 00:00Мб прогнать хотя бы на этом: https://pypi.org/project/OptimizationTestFunctions/ и сравнить с популярными решениями?
Еще раз посмотрите на тестовые функции в этом репозитарии и тестовую функцию в статье
https://www.google.ru/search?q=z+%3D+-(4exp%28-%28x-4%29%5E2+-+%28y-4%29%5E2%29%2B2exp%28-%28x-2%29%5E2+-+%28y-2%29%5E2%29%29%2B4%2B0.2sin%28x%29%2B0.2cos%28y%29&newwindow=1&sxsrf=AJOqlzWlG-mGPnc4Mw7clYhca4XRAHNkhw%3A1678092860366&source=hp&ei=PKoFZKjIE4PprgSCwJaIAw&iflsig=AK50M_UAAAAAZAW4TFjsO9mdlcBJdARHrvUAkbCPrmcE&oq=z&gs_lcp=Cgdnd3Mtd2l6EAEYATIECCMQJzIECCMQJzIECCMQJzIICAAQgAQQsQMyCAgAEIAEELEDMggIABCABBCxAzIICC4QgAQQ1AIyCAgAEIAEELEDMggIABCABBCxAzIICAAQgAQQsQNQAFgAYJ4XaABwAHgAgAGCAYgBggGSAQMwLjGYAQCgAQE&sclient=gws-wiz
Не забудьте выставить диапазоны x,y -100;100Похоже что вы таки решили проблему поиска глобального минимума и знатно подняли качество современных публикаций на тему проблем машинного обучения, это достойно уважения!
Увы, не смог оценить сарказм,
Насчёт эвристики с выбором лучшего. Вот тут как раз не факт, что это как-то ускоряет поиск.
Факт. Эвристики и оптимальный поиск. Просто никто не думает о эвристиках в разрезе простых алгоритмов (вроде градиентного спуска).
вот, кстати, пример метода с multi-start, в котором есть множество алгоритмов локального поиска и делается выбор, каким искать.
Ну, multi-start и global search скорее всего где-то между 100 запусками градиентного спуска и перезапуском при достижении минимума. Ничто не мешает добавить и настройку размера шагов, и прочие полезные вещи. Только с учетом что они тоже должны быть оптимальны.
Это сильное заявление, хотелось бы какое-нибудь обоснование (более серьёзное, чем десять примеров).
В статье же объяснено почему я отказался от свистелок и перделок в виде обучения с моментом, чтобы получить оптимальные градиентные спуски (пусть даже в некоторой области с локальным минимумом).
Так же добавил результаты 300 запусков, сведенные в таблицу.
masai
00.00.0000 00:00На телефоне эта монструозная ссылка бесполезна. :) Сэкономлю немного времени другим читателям и добавлю картинки.


Еще раз посмотрите на тестовые функции в этом репозитарии и тестовую функцию в статье
Ну хорошо, а в чём сложность функции-то? Ярко выраженные локальные экстремумы, градиент везде хороший. Если попал в окрестность — гарантированно попадёшь в локальный оптимум. Извилистых оврагов нет, седловых точек мало.
А вот в том бенчмарке каждая функция в чём-то особенная. Например, функция Розенброка считается трудной для поиска глобального минимума из-за плоского извилистого оврага.
Если сравнивать методы оптимизации, то на каком-то бенчмарке, а не на единственной функции. Ну и раз уж у вас метод глобальной оптимизации, то и сравнивать стоит с методами глобальной оптимизации.
Факт. Эвристики и оптимальный поиск.
Ну хорошо, а чем очередь с приоритетами помогает? Всё равно нужно для каждой точки довести градиентный спуск до конца. Какая разница, в каком порядке это делать? А других эвристик (вернее, оптимизаций) по сравнению с multistart тут и нет.
Просто никто не думает о эвристиках в разрезе простых алгоритмов (вроде градиентного спуска).
Ну как же не задумывается, если для методов вроде вашего целое название придумали? Вы просто не интересовались, наверное.
Вот кусочек из статьи 1985 года:
A.H.G. Rinnooy Ran et al. A STOCHASTIC APPROACH TO GLOBAL OPTIMIZATION

Похоже, правда? Есть много статей — и старых, и новых. Просто погуглите.

masai
00.00.0000 00:00Не требует доказательств, что шанс застрять в локальном оптимуме меньше в N раз, где N - количество начальных точек.
Не очень понятно, как вы это посчитали.
Пусть вероятность застрять в локальном оптимуме равна 2/3.
Тогда если мы делаем N=2 независимые попытки, получаем, что вероятность застрять в обеих равна 2/3 × 2/3 = 4/9. Это меньше, чем исходная вероятность, но не в N раз (иначе была бы 1/3=3/9).

ValeriyPu Автор
00.00.0000 00:00Ну хорошо, а в чём сложность функции-то? Ярко выраженные локальные экстремумы, градиент везде хороший. Если попал в окрестность — гарантированно попадёшь в локальный оптимум. Извилистых оврагов нет, седловых точек мало.
Я проверяю эффективность поиска глобального оптимума, а не настройки размера шага. 1200 локальных минимумов против 1 глобального в интервале [[-100;100],[-100;100]]
Ну хорошо, а чем очередь с приоритетами помогает? Всё равно нужно для каждой точки довести градиентный спуск до конца. Какая разница, в каком порядке это делать? А других эвристик (вернее, оптимизаций) по сравнению с multistart тут и нет.
Ну, если без определения оптимальности - при нормальном распределении размеров ошибки случайно выбранных точек, если мы возьмем точки с наименьшим отклонением от искомого минимума, то сможем проверить большее количество локальных минимумов и быстрее найдем минимум глобальный
Ну как же не задумывается, если для методов вроде вашего целое название придумали? Вы просто не интересовались, наверное.
Погуглил и глобальную оптимизацию, и мультистарт, и стохаотическую глобальную оптимизацию - ничего не нашел ).

masai
00.00.0000 00:00Я проверяю эффективность поиска глобального оптимума, а не настройки размера шага.
Посмотрите, пожалуйста, бенчмарк. Там почти половина функций мультимодальные. Если открыть репозиторий на GitHub, то там есть графики.
То, что вы подобрали функцию, на которой ваш конкретный алгоритм работает лучше какого-то другого алгоритма (из другого класса), называется в науке cherrypicking. Бенчмарк существует для того, чтобы можно было сравнивать методы оптимизации. Каждая функция там сложна в чём-то своём. Что толку от алгоритма, если на вашей функции он хорошо сходится, а на остальных нет?
Мы так долго спорим, что вы уже запустили бы давно. :)
1200 локальных минимумов против 1 глобального в интервале [[-100;100],[-100;100]]
Какая разница, сколько их? Главное — особенности ландшафта. Например, на функции Stairs из бенчмарка ваш алгоритм найдёт единственный минимум только если точка сразу в него попадёт, так как градиент почти всюду нулевой.
Ну, если без определения оптимальности - при нормальном распределении размеров ошибки случайно выбранных точек, если мы возьмем точки с наименьшим отклонением от искомого минимума, то сможем проверить большее количество локальных минимумов и быстрее найдем минимум глобальный
А очередь как помогает? Вы всё равно должны каждую точку довести до конца, чтоб убедиться, что это не глобальный минимум.
Погуглил и глобальную оптимизацию, и мультистарт, и стохаотическую глобальную оптимизацию - ничего не нашел ).
Я только в этих комментариях две статьи скинул. Второй 38 лет в этом году будет и она описывает ваш метод, который в то время был хорошо известен.
У нас какой-то разный гугл. Я просто пишу "multistart global optimization" и мне вываливает кучу статей. Это я даже в Google Scholar и arXiv не предлагал ещё. :)
Вот, первая попавшаяся же статья рассказывает, что ещё в 1970 году предложили модификацию вашего алгоритма. Почему нужно кидать много точек? Чтоб попасть в бассейны разных минимумов. И вот предложили сперва кидать равномерно, а потом смотреть, какие точки собираются в кучку после нескольких шагов. Если они собираются в кластер, то можно только одну точку рассматривать, а остальным назначить низкий приоритет. Этот метод был очень популярен в 70-х.
Вы безусловно молодец, что придумали multistart, но если вы почитаете какие-то обзоры, а лучше учебник по методам оптимизации, то это поможет вам не повторять то, что уже было изобретено.
Ну и насчёт машинного обучения. Multistart не используется не потому, что никто не додумался, а потому что это нерационально. Слишком много вычислительных ресурсов ради сомнительного улучшения. Методы второго порядка вот практически не используются для обучения нейронных сетей. Тут с Adam бы обучить.

ValeriyPu Автор
00.00.0000 00:00Вы безусловно молодец, что придумали multistart
а потом смотреть, какие точки собираются в кучку после нескольких шагов
Вот в двух словах вы и определили, чем отличается мой алгоритм. Правильно, это оптимальный поиск.
Без момента, "бассейнов" и прочего.
Почему? потому что с точки зрения анализа алгоритмов и функций по N точкам нет никакихособенности ландшафта
Определяя эти бассейны, мы не можем сказать, что ДА, МЫ ВЗЯЛИ 10 ТОЧЕК, и ВРОДЕ ОНИ СТЯГИВАЮТСЯ, И ЭТО БАССЕЙН. И ВСЕ ТОЧКИ ТУТ - БЕСПОЛЕЗНЫ.
То же самое с моментом и остальными оптимизациями.(Кстати, multistart matlab-a находит глобальный минимум предложенной функции 0% раз )
Спасибо за то, что привели правильное название - глобальная оптимизация.
Кстати, мой алгоритм чуть ли не в 1% лучших (я могу решить Damavandi за 2000 измерений ошибки в 76% случаев)
https://infinity77.net/global_optimization/test_functions.html#test-functions-index
https://infinity77.net/global_optimization/test_functions_nd_D.html
Кстати, представленная тестовая функция похожа на смесь самых плохо решаемых
А очередь как помогает?
Уже приводил пример, даже понятную аналогию давал
при нормальном распределении размеров ошибки случайно выбранных точек, если мы возьмем точки с наименьшим отклонением от искомого минимума, то сможем проверить большее количество локальных минимумов и быстрее найдем минимум глобальный

masai
00.00.0000 00:00Без момента, "бассейнов" и прочего.
Про момент я ничего не говорил, но бассейн у вас очень даже есть. :)
Бассейн локального минимума (attraction basin) — это такая область, что при выборе начальной точки из него, градиентный спуск попадёт именно в этот локальный минимум. Вы же не будете отрицать, что его нет. :)
Определяя эти бассейны, мы не можем сказать, что ДА, МЫ ВЗЯЛИ 10 ТОЧЕК, и ВРОДЕ ОНИ СТЯГИВАЮТСЯ, И ЭТО БАССЕЙН. И ВСЕ ТОЧКИ ТУТ - БЕСПОЛЕЗНЫ.
Прочитайте, пожалуйста, внимательно моё сообщение (а лучше исходную статью). Я нигде не говорил, что эти точки бесполезны, я говорил, что можно выбрать приоритеты. Можно рассматривать одну, если не позволяют вычислительные ресурсы.
Или, если позволяют, можно использовать эту информацию, чтобы выбрать другие точки. Равномерное распределение — это некоторое априорная оценка. Используя апостериорную информацию, можно улучшить оценку и добавить точки из других бассейнов.
Кстати, мой алгоритм чуть ли не в 1% лучших
Среди каких алгоритмов? :)
Если вы запустили его на бенчмарке, то приведите, пожалуйста, таблицу с параметрами запуска (область поиска и число точек), указанием количества вычислений функции и полученного значения. Тогда можно будет сравнить с другими методами оптимизациями.
А пока что это просто слова. Наука так не делается.
Кстати, multistart matlab-a находит глобальный минимум предложенной функции 0% раз
А для какого числа точек и какой области поиска вы запускали? :) Это точно было честное сравнение? А то если вы использовали 100 точек для своего алгоритма и 10 для матлаба, то сравнение некорректное.
А какие ещё методы глобальной оптимизации вы пробовали запускать?
Уже приводил пример, даже понятную аналогию давал
Похоже, вы не поняли вопрос. Попробую объяснить ещё раз.
У вас в алгоритме каждая точка обрабатывается до тех пор, пока не выполнится одно из условий:
Очередь пуста. Это значит, что все точки обработаны. А раз они все обработаны, то очередь не нужна, так как она влияет только на порядок обработки. То есть, это обычный multistart, хорошо известный метод.
Закончилось число итераций. А вот тут очередь помогает, так как хоть вы и не нашли минимум (иначе бы у вас была ситуация 1), но у вас будет лучшая на данный момент оценка. Но тут возникает риск, что если у вас много точек, то вы можете не дойти даже до локального минимума.
Если вы думаете, что никто не использует очередь с приоритетами при оптимизации, то вы ошибаетесь. Например, метод ветвей и границ основан на этом, да и другие методы оптимизации. Это не какое-то откровение. Часто очередь просто не упоминают, так как это просто деталь реализации.
(Кстати, вместо случайных начальных точек лучше использовать последовательности с низким расхождением. Например, последовательность Соболя.)
В байесовской оптимизации пошли ещё дальше и назначают приоритеты вообще всем точкам из области поиска. :)
Без обид, но давайте вы всё же что-то прочитаете. Потому что пересказывать всё очень утомительно. У вас очень выгодная позиция: вы можете говорить всё, что в голову придёт, а мне приходится подробно объяснять. Доказательствами вы, как я понимаю, себя не утруждаете, несмотря на то, что, например, с уменьшением шансов в N раз ошиблись.
Не знаю, насколько мне хватит мотивации. Честно говоря, для меня не очень важно, правы вы или нет. Если хотите, то можете считать свой алгоритм лучшим в мире, а меня частью заговора учёных, я не против. Если же хотите действительно разобраться, то попробуйте следовать научному подходу: подкреплять утверждения доказательствами или результатами воспроизводимых экспериментов.

ValeriyPu Автор
00.00.0000 00:00У вас очень выгодная позиция: вы можете говорить всё, что в голову придёт, а мне приходится подробно объяснять.
Именно. Я могу просто добавить операцию обновления очереди и получить начальные точки такие же или лучше, и улучшить результат еще на десять процентов.
Не прибегая к предположениям о бассейнах и их позициях, о том что точки в каком-то месте неизвестной (все еще) функции лучше\хуже остальных.
Достаточно предположений:Что градиентный спуск точки с меньшей ошибкой приводят к еще меньшей ошибке.
Считать изменение положения точки на плато\в локальном минимуме смысла нет.
Хотя результат уже довольно интересен, особенно если сравнить с Mutistart (100 точек по 20000 шагов).
Конечно, я могу добавить к своему получившемуся алгоритму все о чем вы говорите - и байесовскую оптимизацию гиперпараметров, и какие-то иные предположения "о бассейнах".
Но это не строгие предположения, и я могу просто "отсечь" части с глобальным оптимумом. Благодаря "очевидному ландшафту функции с известными особенностями", как вы говорили. И не получить решения в принципе.Поэтому и не рекомендуется применять подобные техники. Но мне ничто не запрещает прикрутить все это к имеющемуся алгоритму. И быстро и эффектно делать вид оптимального поиска глобального минимума :).
У вас в алгоритме каждая точка обрабатывается до тех пор, пока не выполнится одно из условий:
Где это написано? Очередь всегда есть, с некоторым количеством точек.





Ktator
Это сильное заявление, хотелось бы какое-нибудь обоснование (более серьёзное, чем десять примеров).
Что были за функции? Какая у них размерность? И какие результаты показывать обычный градиентный спуск? А что будет если мы увеличим размерность на порядок? А вы пробовали обучать нейросети из той статьи, которая вам так не понравилась?