Учим нейросеть играть в Шахматы, загрузив в нее датасеты уже сыгранных партий с известным результатом.

То есть никакого минимакса, деревьев и расчетов на несколько ходов вперед.
Идея в том, что если в нейросеть загрузить много партий, уже сыгранныx другими игроками, то нейросеть будет знать, как поступали другие игроки в соответствующих случаях и к какому результату это приводило. Нейросеть обобщит имеющийся опыт и будет делать ход на основе уже известного опыта и выявленных закономерностей, причем делать ход «мгновенно».

Понимаем, что в более общем случае датасет — это имеющийся опыт поведения множества объектов, в том числе мировой и в том числе многолетний, а Шахматы — частный случай модели принятия решений с учетом известных ограничений

Таким образом, более общая идея заключается в том, что можно научить нейросеть принимать решения на основе уже известного опыта. В итоге нейросети смогут обобщать имеющийся мировой опыт поведения в различных ситуациях и уже на основе имеющегося опыта принимать оптимальные решения.Так нейросеть будет обучаться как человек — при погружении в новую тему не начинать все с самого нуля, а прочитать литературу по теме, ознакомиться с уже имеющимися данными и результатами и оперативно впитать в себя уже известный многолетний опыт множества людей.

Дополнительный интерес заключается в том, что нейросеть будет играть на уровне загруженного датасета, а если загрузить партии выбранного гроссмейстера, то и на уровне гроссмейстера и даже в его стиле. Другими словами, нейросеть учится очень быстро — не годами тренировок, а просто впитыванием в себя и обобщением уже известного опыта других участников.

Если убрать «антураж», то в общем виде получаем стандартные для машинного обучения задачи классификации и ранжирования. Соответственно, и решать начнем «стандартными» способами.

Общий ход реализации

1. загружаем датасет сыгранных партий (история, результат);

2. кодируем комбинации на доске по истории партий;

3. дополнительно размечиваем комбинации с точки зрения итога партий;

4. обучаем нейросеть на основе имеющихся комбинаций и меток классов.

Конечно, в идеале было бы не давать модели даже правила игры. Пусть нейросеть самостоятельно так выискивает закономерности, что даже сама ходит по правилам. Но это уже на следующем уровне, на первом же этапе принудительно ограничим выбор модели имеющимися правилами.

Как кодировать данные

Стандартный и важнейший вопрос при обработке данных - в каком виде предоставить данные для обучения.

Распространенным вариантом кодирования положения на шахматной доске является FEN, пример выглядит так:

rnbqkbnr/pp4pp/2p1p3/8/3P4/5N2/PP2PPPP/RNBQKB1R b KQkq - 1 5

Также есть различные варианты записи истории ходов, пример выглядит так:

d4 Nc6 e4 e5 f4 f6 dxe5 fxe5 fxe5 Nxe5 Qd4 Nc6 Qe5+ Nxe5 c4 Bb4+

Конечно, в таком виде данные в сеть не передать. Нужно оцифровывать.

У нас 64 клетки поля и 12 фигур.

В таком случае можно назначить цифру каждой клетке поля и каждой фигуре.

Тогда положение на доске принимает уже более привычный вид для обработки данных:

[2, 3, 4, 5, 6, 4, 3, 2, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 7, 7, 7, 7, 7, 7, 7, 7, 10, 8, 9, 11, 12, 9, 8, 10]

Обязательно следует поэкспериментировать с тем, каким образом назначать цифры. Все числа подряд, или ряд Фибоначчи, или пешки к пешкам, или One‑Hot‑Coding и так далее. Все это следует перебрать и протестировать. Займемся этим на этапе тюнинга и улучшений, а стартовать нужно хоть с чего‑то, чтобы представлять общую картину, поэтому для старта пусть все числа идут подряд.

Готовим данные

Программируем на python в Colab

Нашли условно подходящий открытый датасет на Kaggle.

name = 'sample_data/games.csv'
colums = ['id','rated','created_at','last_move_at','turns','victory_status','winner','increment_code','white_id','white_rating','black_id','black_rating','moves','opening_eco','opening_name','opening_ply']
df = pd.read_csv(name, names = colums )

Создаем массивы данных.

# создаем массивы данных

print('Started...')

combination_code = ''

histories = []                  # массив историй
status = []                     # массив статусов партий
x = []                          # массив комбинаций в собственной кодировке доски            
y = []                          # массив результатов партии (победа/поражение) с комбинациями x
fen_massive = []                # массив в кодировке fen
fen_and_code_combination = []   # массив совместный в кодировке fen и в собственной кодировке доски

PIECE_SYMBOLS_NEW = ['.','P','R', 'N','B','Q','K','p','n','b', 'r','q','k']
def piece(cell): return str(board.piece_at(cell)) if str(board.piece_at(cell)) != 'None' else '.'

# готовим набор историй
histories = [ key for key in df.moves]
histories.pop(0)

# готовим набор классов
status = [ 1 if key == 'white' else 0 for key in df.winner]
status.pop(0)

# запускаем цикл прохода по историям
for histories_index, this_history in enumerate(histories):
  if histories_index % 1000 == 0: print(histories_index)

  # запускаем партию заново
  board=chess.Board()
  fen = board.fen()
  combination_code = [PIECE_SYMBOLS_NEW.index(piece(cell)) for cell in range(64)] 

  # для теста и демонстрации берем первые 10, чтобы сократить время
  for index, key in enumerate(histories[histories_index].split()[:10]):
    
    # как бы делаем ход
    board.push_san(key)

    # фиксируем только ситуацию для белых, поэтому смотрим четную запись
    if index % 2 == 0: 
      fen = board.fen()
      combination_code = [PIECE_SYMBOLS_NEW.index(piece(cell)) for cell in range(64)]

      # добавляем значения в массивы 
      x.append(combination_code)
      y.append(status[histories_index])
      fen_massive.append(fen) 
      fen_and_code_combination.append([fen, combination_code])

print('Finished')

На данный момент у нас 20058 историй и в них 98787 комбинаций. При этом для сокращения времени на старте берем в истории только первые 10 записей, то есть только первые 5 ходов.

Теперь нужно вытащить уникальные комбинации и снабдить их показателями.
Считаем комбинацию "успешной", если процент побед превышает 0.5, и "неуспешной" в ином случае.

# создаем массив уникальных комбинаций fen
fen_massive_unicum = list(set(fen_massive))

# создаем массив уникальных комбинаций fen с подсчетом количества побед
# столбцы: fen, общее количество, количество побед, количество поражений, процент победных

print('Started...')

fen_massive_unicum_counter = []

# формируем список с fen нужным количеством столбцов
for key in fen_massive_unicum:
  fen_massive_unicum_counter.append([key, 0,0,0,0])

# теперь загоняем в него показатели
for index, key in enumerate(fen_massive_unicum_counter):
  if index % 1000 == 0: print(index)
  for index2, key2 in enumerate(fen_massive):
    if key[0] == key2:
      key[1] += 1
      if y[index2] == 1: key[2] += 1 
      else: key[3] += 1
      key[4] = key[2]/key[1]

print()
print('Finished')

Получаем 27 536 уникальных комбинаций с показателями успешности.

Возможно, стоило бы выделить 3 класса: победа, проигрыш, ничья. Также возможно, стоило бы выделить еще больше классов, например, по длительности партии. То есть комбинация еще более успешная, если игра закончилась быстро, но это на этапе последующих улучшений. Для старта оставляем всего два класса: победа / не победа.

Возможные аномалии

Понимаем, что наш датасет абсолютно сырой и возможны различные аномалии.

Предварительно примеры возможных аномалий:

1. Мы не знаем реальное качество партий. Партии могут быть такими, что качество комбинаций в них может не коррелировать с конечным результатом партии.

2. Игрок может сделать откровенно слабый ход, а потом собраться и выиграть партию. В итоге комбинация будет считаться «успешной». И наоборот, возможен сильный ход и очень сильное положение на доске, но по итогу игрок проиграл, комбинация будет считаться «неуспешной».

3. Некоторые ходы встречаются очень много раз. И некоторые комбинации встречаются очень много раз. Если комбинация встречается несколько тысяч раз и у нее показатель успешности 0.55, то на это уже можно ориентироваться. А если игрок сделал редкий ход, и при этом выиграл, то в итоге комбинация встречается 1 раз, и у нее показатель побед 100%. Понимаем, что применение комбинации всего 1 раз ничего не говорит о ее успешности, но с точки зрения применяемого подхода, это очень успешная комбинация и модель будет ее рекомендовать. То же самое и комбинациями, которые встречаются, например, 3 раза. Показатель успешности может быть 0.67, и это очень успешная позиция, хотя на самом деле может таковой и не являться. То есть нужно определять, какие ходы «шумят» и убирать их из обучения.

Таким образом, со временем применяемые датасеты нужно будет «чистить». В идеале, чтобы именно комбинация получала оценку специалистов. Ну а стартовать будем с реальным «грязно‑шумным» датасетом. Заодно и посмотрим, с чем столкнемся при получении сырых датасетов с реальных шахматных соревнований.

Показатели успешности первого хода

Ради интереса посмотрим на показатели самого первого хода.

# смотрим доступные ходы первого хода белых

# в начало партии
board=chess.Board()
fen = board.fen()

win_percent = []
legals = []

# первый  слой доступных ходов
for key in board.legal_moves: 
  legals.append(str(key))

# перебираем доступные ходы
for index, legal_move in enumerate(legals):
  board.push_san(legal_move)
  fen = board.fen()

  #ищем комбинации
  for key in fen_massive_unicum_counter:
    if fen == key[0]:
      print(index,'move:',legal_move, 'total:', key[1], 'wins:', key[2], 'percent:', key[4])
      win_percent.append([legal_move, key[1], key[4]])
      
      break
  board.pop()    

print()  
print('len(win_percent):', len(win_percent))

0 move: g1h3 total: 15 wins: 9 percent: 0.6
1 move: g1f3 total: 725 wins: 373 percent: 0.5144827586206897
2 move: b1c3 total: 99 wins: 42 percent: 0.42424242424242425
3 move: b1a3 total: 4 wins: 1 percent: 0.25
4 move: h2h3 total: 14 wins: 7 percent: 0.5
5 move: g2g3 total: 186 wins: 85 percent: 0.45698924731182794
6 move: f2f3 total: 23 wins: 8 percent: 0.34782608695652173
7 move: e2e3 total: 416 wins: 142 percent: 0.34134615384615385
8 move: d2d3 total: 131 wins: 50 percent: 0.3816793893129771
9 move: c2c3 total: 56 wins: 31 percent: 0.5535714285714286
10 move: b2b3 total: 173 wins: 82 percent: 0.47398843930635837
11 move: a2a3 total: 27 wins: 17 percent: 0.6296296296296297
12 move: h2h4 total: 33 wins: 6 percent: 0.18181818181818182
13 move: g2g4 total: 38 wins: 11 percent: 0.2894736842105263
14 move: f2f4 total: 166 wins: 68 percent: 0.40963855421686746
15 move: e2e4 total: 12598 wins: 6371 percent: 0.50571519288776
16 move: d2d4 total: 4522 wins: 2258 percent: 0.49933657673595755
17 move: c2c4 total: 716 wins: 383 percent: 0.5349162011173184
18 move: b2b4 total: 88 wins: 48 percent: 0.5454545454545454
19 move: a2a4 total: 28 wins: 9 percent: 0.32142857142857145

len(win_percent): 20

Видим, что на все 20 доступных ходов первого хода белых есть данные: игрались столько-то раз и с таким-то успехом.

В общем-то показатели соответствует общепринятой шахматной логике. Видно, что чаще всего первым ходом с огромным перевесом играют e2e4, потом по количеству повторов идет d2d4, потом рядышком g1f3 и c2c4 и где-то далеко потом все остальное. При этом e2e4, g1f3 и c2c4 превышают 0.5, у а d2d4 очень близко, на грани погрешности (0.499), то есть да, ходы сильные, приводят к победе и потому так часто применяются. Также видим и откровенно редкие, и откровенно слабые, то есть в данном случае "неуспешные" ходы.

Интересно, что не у самых распространенных и при этом не самых редких ходов показатели успешности могут быть выше, чем у самых распространенных. Ход c2c3, например, довольно средний по повторяемости, но при этом 0.55 по успешности, то есть выше, чем e2e4 и c2c4. Как это возможно трактовать? Возможно, что самыми распространенными ходами играть условно легче и стабильнее, но и черные научились против них хорошо защищаться, а вот более редкие варианты у черных уже менее проработаны, а белые специально тренировались, поэтому в конкретных случаях выигрывают чаще. Но, как говорится в известной шутке, это не точно. Или, академическим языком, это гипотеза.

Так или иначе, было бы хорошо, если бы на все ходы была бы такая же таблица и было бы возможно просто выбирать самый успешный ход. Однако на практике наблюдается такое количество вариантов, что в датасете их просто нет. Поэтому будем обучать модель выявлять закономерности успешных ходов и делать соответствующие ходы с учетом выявленных закономерностей.

Готовим данные для анализа второго хода

Для начального тестирования рассматриваем сторону белых.

Понимаем, что обучать модель на 20 позициях нет никакого смысла, поэтому для примера и тестирования будем обучать со второго хода.

Создаем массив уникальных комбинаций второго хода белых с показателями успешности.

# создаем массив из вторых ходов белых

fen_massive_unicum_counter_2 = []
for key in fen_massive_unicum_counter:
  if key[0][-1] == '2' and key[0][-2] == ' ':
    fen_massive_unicum_counter_2.append(key)

Получаем 962 уникальные комбинации второго хода белых с показателями успешности.
Понимаем, что следует брать датасеты и поувесистей, ну а для старта вполне достаточно.

Нехитрым перебором получаем, что общее количество доступных комбинаций на втором ходе белых составляет 8902, а в нашем датасете есть только 962. Видим, какая примерно часть реально «проработана игроками», а какая будет для нейросети новой.

Создаем массив соответствий уникальных комбинаций fen и собственной кодировки доски.

# создаем массив уникальных fen из вторых ходов белых

fen_massive_unicum_2 = []
for key in fen_massive_unicum_counter_2: 
    fen_massive_unicum_2.append(key[0])

# приводим в соответствие уникальные fen второго хода белых и собственную кодировку

fen_and_combination_code_unicum_2 = []
for key in fen_massive_unicum_2:
  for key2 in fen_and_code_combination:
    if key == key2[0]:
      fen_and_combination_code_unicum_2.append([key, key2[1]])
      break   

В принципе, мы могли бы сразу добавить собственную кодировку в общий массив fen_massive_counter, но это представляется неудобным, так как с кодировками возможна отдельная работа, поэтому лучше отдельно вести работу с кодировками, а отдельно иметь общее место, где они находятся в соответствии. Так возможно впоследствии проводить сопоставление при любых последующих преобразованиях кодировок. В общем, это возможно при необходимости улучшить, а пока для идентификации оставляем так.

Готовим привычные x_train, y_train.

x_train будет представлять набор сыгранных комбинаций второго хода белых.

train традиционно будет содержать метку класса, причем 1, если побед больше 0.5, и 0 в обратном случае.

# создаем массив комбинаций в собственной кодировке для последующей передачи в модель
x_train_2 = [ key[1] for key in fen_and_combination_code_unicum_2 ]

# создаем массив меток для последующей передачи в модель
y_train_2 = [ ( 1 if key[4] > 0.5 else 0 )for key in fen_massive_unicum_counter_2 ]

# переводим x_train_2 в цифры и массив numpy 
x_train = np.array([ [ int(key2) for key2 in key  ] for key in x_train_2  ])

# переводим y_train_2 в цифры и массив numpy 
y_train = np.array([int(key) for key in y_train_2])

Данные готовы, можно переходить к модели.

Обучаем модель второму ходу

По сути решаем стандартные задачи классификации и ранжирования.

Чтобы примериться, начнем «условно стандартно» для задач подобного рода — нейронная сеть прямого распространения, 128 признаков, Adam, sigmoid, binary_crossentropy

model_1 = keras.Sequential([
    Dense(128, activation='relu', input_shape=(64,)),
    Dense(1, activation='sigmoid')
])

myAdam = keras.optimizers.Adam(learning_rate=0.0001)
model_1.compile(optimizer=myAdam,
             loss='binary_crossentropy',
             metrics=['accuracy'])

Epochs = 100
history_1 = model_1.fit(x_train, y_train, batch_size=32, epochs=Epochs, validation_split=0.2)

Пример первых запусков:

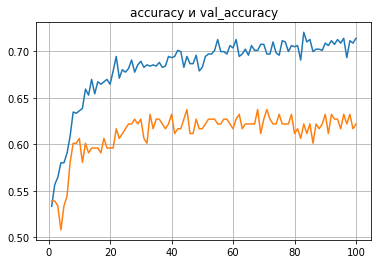
Видим, что модель ведет себя «как по учебнику», то есть ошибка тренировочной выборки постепенно уменьшается, а ошибка валидационной выборки уменьшается 20–30 эпох и зависает. Соответственно точность тренировочной выборки постепенно повышается, а точность валидационной выборки повышается 20–30 эпох и зависает.

Предварительная трактовка первых запусков

1. Сразу же, при запуске «в лоб», получили точность валидационной выборки порядка 63%. Что это означает? При определении цифр на изображении паспорта точность даже в 90% будет недостаточной. Это будет означать, что будет ошибка при обработке каждого паспорта, и сама идея такой обработки теряет смысл. А если играть в казино на чет / нечет с точностью более 60%, то это «золотая жила». В данном случае полученный результат означает, что в 63% случаев модель будет делать «успешный» ход на уровне загруженного датасета. И это без тюнинга, архитектуры и подбора гиперпараметров. Понимаем, что модель в целом рабочая, и дальше можно тюнинговать и улучшать, и в общем‑то понятно, как именно это делать.

2. В данном датасете 962 уникальные комбинации второго хода для белых, и при этом 402 комбинации, которые игрались всего 1 раз. Понимаем, насколько они «шумят» и вносят путаницу. Соответственно, «чистка» датасета еще больше улучшит точность.

Ключевой и переломный момент

Нехитрым перебором получаем оценки модели для всех возможных комбинаций второго хода белых, и уже видим интересные результаты.

Если принудительно походить за модель первым ходом e2e4, то в большинстве случаев после ответного хода черных модель будет выводить слона f1c4, что в общем‑то соответствует шахматной логике многих партий. И это без минимакса, без книги дебютов, без подсчета общей стоимости фигур, без подсчета атакуемых и защищаемых полей и прочее и прочее. Модель просто посмотрела (!) на вторые ходы сыгранных партий с известным результатом, и «сама решила», что после e2e4 нужно выводить слона f1c4. В общем, это возможно признать ключевым и переломным моментом, потому как видно, что концепт рабочий, и дальше только «рутина» по улучшению.

Другие наблюдения:

1. d2d4, g1f3 после «принудительного» первого хода c2c3

2. d2d4, g1f3, b1c3 после «принудительного» c2c4

3. d2d4, g1f3, c2c4 в большинстве случаев после «принудительных» «левых» первых ходов

4. вывод слона f1c4 во многих случаях после «принудительных» e2e3 или d2d3

5. вывод слона c1b2 или c1a3 после «принудительных» b2b3 или b2b4

Еще раз обратим внимание: это не перечень часто встречающихся ходов, взятых из таблицы по количеству повторов, а это модель сама выбрала эти ходы, подобрав соответствующие коэффициенты в ходе машинного обучения!

Конечно, не обошлось и без «ляпов».

Например, после «принудительных» d2d3 или d2d4 модель ходит то c1f4, то c1h6. С одной стороны, возвращаемся к абзацу про аномалии датасета. С другой стороны — а является ли ход c1h6 действительно таким слабым. Это мне на моем любительском уровне ход кажется слабым, точнее — непревычным, а модель решила одной жертвой сдвоить оппоненту пешки на крайней линии, заблокировать ладью, лишить коня и слона выхода на h6 — непревычно, но не так уж и однозначно.

В общем видим, что в большинстве случаев модель ведет себя достаточно адекватно и делает «вполне осмысленные» ходы, соответствующие распространенным шахматным дебютам, и это всего лишь после того, как пару минут посмотрела на игру других игроков и результаты партий. То есть в полном смысле слова научилась, наблюдая за другими.

Базовый принцип анализа ходов

Базовый принцип анализа ходов одинаков: готовим из датасета выборку для данного хода (также как и для второго хода) и запускаем модель.

Например, для пятого хода это будет так:

# создаем массив с пятым ходом белых
fen_massive_unicum_counter_5 = []
fen_massive_unicum_counter_5 = [ key for key in fen_massive_unicum_counter if key[0][-1] == '5' and key[0][-2] == ' ' ]

# создаем массивы аналогично

fen_massive_unicum_5 = []
for key in fen_massive_unicum_counter_5: 
    fen_massive_unicum_5.append(key[0])

fen_and_combination_code_unicum_5 = []
for key in fen_massive_unicum_5:
  for key2 in fen_and_code_combination:
    if key == key2[0]:
      fen_and_combination_code_unicum_5.append([key, key2[1]])
      break    

x_train_5 = [ key[1] for key in fen_and_combination_code_unicum_5 ] 
x_train_move5 = np.array([ [ int(key2) for key2 in key  ] for key in x_train_5 ])     

y_train_5 = [ ( 1 if key[4] > 0.5 else 0 )for key in fen_massive_unicum_counter_5 ]
y_train_move5 = np.array([int(key) for key in y_train_5])

model_test_move5 = keras.Sequential([
    Dense(128, activation='relu', input_shape=(64,)),
    Dense(1, activation='sigmoid')
])

myAdam = keras.optimizers.Adam(learning_rate=0.0001)
model_test_move5.compile(optimizer=myAdam,
             loss='binary_crossentropy',
             metrics=['accuracy'])

Epochs = 20
history_test_move5 = model_test_move5.fit(x_train_move5, y_train_move5, batch_size=32, epochs=Epochs, validation_split=0.2)

В принципе, на данном этапе результаты по ходам схожие.

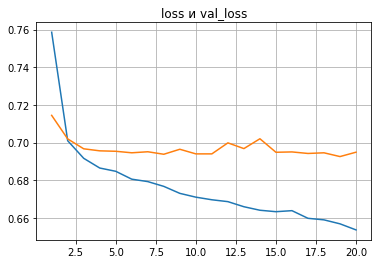
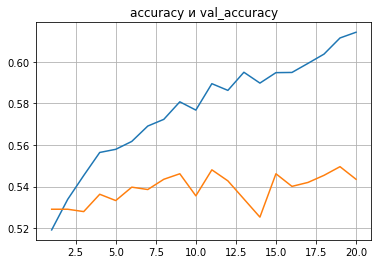
Возможно, делать выборку по каждому ходу не совсем оптимально.

С другой стороны, объединить все ходы в одну выборку тоже неправильно, поскольку закономерности, например, в начале партии на 2–4 ходах могут сильно отличаться от закономерностей на 10-х ходах и 20-х ходах. В конечном итоге на этапе тюнинга и улучшений следует подобрать параметры «скользящего окна», то есть, например, для анализа 20-го хода обобщать закономерности 19–21 ходов.

Как нейросеть делает ход

Начало партии задается одинаково:

# самое начало
board=chess.Board()
fen = board.fen()

Далее в любой момент ход делается командой из библиотеки, например:

this_move = 'e7e5'
board.push_san(this_move)
board

А модель ходит так:

# играет модель

legals = []
recom = []

# первый  слой доступных ходов
for key in board.legal_moves: 
  legals.append(str(key))

# перебираем доступные ходы
for index, legal_move in enumerate(legals):
  
  board.push_san(legal_move)
  fen = board.fen()
  combination_code = [PIECE_SYMBOLS_NEW.index(piece(cell)) for cell in range(64)] 
  x_analised = np.array([ int(key) for key in combination_code ])
  x = np.expand_dims(x_analised, axis=0)

  # вот здесь пишем название применяемой модели
  res = model_1.predict(x, verbose=0)
  recom.append([legal_move, res[0][0]])

  board.pop()

print()

# печатаем ход и оценку
ind = np.argmax([ key[1] for key in recom ])
print(recom[ind])
print()

# делаем ход
board.push_san(recom[ind][0])

# выводим изображение доски
board

То есть модель смотрит доступные ходы для данной ситуации (обычно их порядка 20–30), прогоняет доступные ходы через коэффициенты, полученные на этапе обучения, и выбирает самый «успешный» ход, то есть ход, максимально приближенный к 1.

Посмотреть все ходы в порядке убывания возможно так:

# смотрим все доступные ходы в порядке уьывания оценки
for key in reversed(np.argsort([ key[1] for key in recom  ] )):
  print(recom[key])

Результат. Общий вывод.

Концепт рабочий, в большинстве случаев модель (прототип) ведет себя достаточно адекватно и делает «вполне осмысленные» ходы.

Расчеты делаются не во время самой игры, на что тратились бы драгоценные секунды, а заранее, во время обучения, во время же игры модель смотрит только ближайший уровень ходов, прогоняя их через полученные ранее коэффициенты.

Во время игры модель отвечает «мгновенно», и это всего лишь после того, как модель посмотрела на игру других игроков и результаты партий. То есть в полном смысле слова научилась, наблюдая за другими.

В общем, начало положено. Дальше только повышать точность.

Как повышать точность.

Для повышения точности запланировано следующее:

1. Тестирование нескольких слоев и различных сочетаний гиперпараметров.

2. Тестирование сверточных слоев для анализа фрагментов.

3. Тестирование рекурентных принципов для возможного анализа последовательностей.

4. Добавление принципов Embedding и Attention для кодирования позиции.

5. «Чистка» загружаемых датасетов.