Меня все время сильно смущало, что в градиентных алгоритмах инициация весов происходит как-то "небрежно" - случайным образом. Для математика, привыкшего к четкости, это было как-то сомнительно. Итак, задача - сравнить результаты различных вариантов инициации - стандартной рандомной и некоторых фиксированных.

Исходные данные

Широкоизвестный датасет MNIST (изображения рукописных цифр).

Подготовка данных достаточно подробно представлена во многих статьях, поэтому не акцентирую на этом внимание, просто предоставляю для ясности, чтобы не было вопросов и сомнений по ходу эксперимента.

(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train / 255
x_test = x_test / 255
y_train_cat = keras.utils.to_categorical(y_train, 10)
y_test_cat = keras.utils.to_categorical(y_test, 10)

Модель

FNN c одним скрытым слоем.

Конечно, FNN - не лучшее решение непосредственно для распознавания изображений, но в данном случае нет задачи достичь лучшей обобщающей способности и лучшей точности, а задача - проанализировать поведение на известном стабильном датасете, желательно без излишних осложнений.

Код самый стандартный:

model_test = keras.Sequential([
  Flatten(input_shape=(28, 28, 1)),
  Dense(numberofneurons, activation='relu'),
  Dense(10, activation='softmax')
  ])

только с принудительной инициацией весов:

kernel_initializer=keras.initializers.Constant(value=weights[n])

Запуск также самый стандартный:

  model_test.compile(
      optimizer='adam',
      loss='categorical_crossentropy',
      metrics=['accuracy']
      )

  history_test = model_test.fit(x_train, y_train_cat, batch_size=batchsize, epochs=EPOCHS, validation_split=0.2, verbose = 0 )
  res = model_test.evaluate(x_test, y_test_cat) 

Ход эксперимента

В качестве значений инициации берем 4 константы, отличающиеся в 2 раза от соседних, и один рандом:

weights = ['n','0.1','0.2','0.4','0.8']

и запускаем модель с каждым значением по 5 раз.

Сначала на 10 эпох.

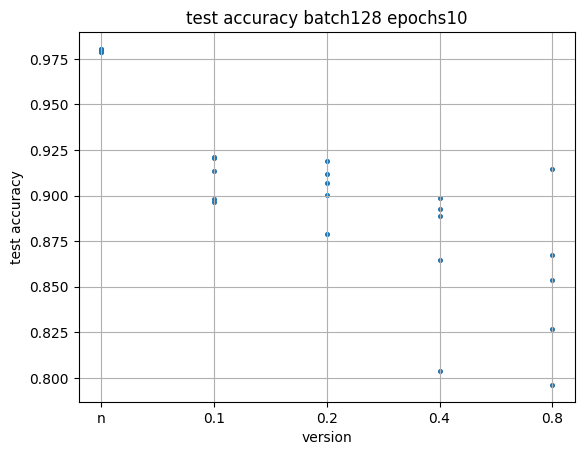
Видно, что результаты рандомных инициаций расположились весьма кучно, и выше остальных. Хуже всех и разбросаннее всех оказались результаты с инициацией 0.8 (самое большое значение). Возможно, что начали слишком из далека, и за 10 эпох значения не успели приблизиться к оптимальным.

Увеличиваем число эпох до 40.

Снова видно, что результаты рандомной инициации легли компактнее и выше всех. При этом результаты инициации 0.1 (соседней) также скучковались и приподнялись, а результаты инициации 0.8 (самое большое значение) все еще хуже всех и разбросаннее всех.

Увеличиваем число эпох до 100.

Уже ожидаемо подтянулись и скучковались результаты инициации 0.2, а результаты инициации 0.8 все также хуже всех и разбросаннее всех.

Можно сделать вывод о том, что 0.4 и 0.8 - сильно большие значения для начала, и с них алгоритму очень далеко до оптимальных значений.

Не будем дальше увеличивать количество эпох, а уменьшим значения в 10 раз, и повторим эксперимент.

weights = ['n',0.01,0.02,0.04,0.08]

Видно, что все результаты стали покомпактнее и повыше.

При этом очевидно, что чем меньше значения инициации, тем лучше результаты, а лидером все еще является рандомная инициация.

Уменьшим значения инициации еще в 10 раз.

Видно, что результаты всех инициаций уже очень близко друг к другу и разбросаны примерно одинаково, хотя рандомная все еще лучше всех, а 0.008 (то есть самое большое значение) все еще хуже всех.

Уменьшим значения инициации еще в 10 раз.

И тут видно, что результаты всех инициация находятся практически в одном интервале и одинаково разбросаны, то есть результат рандомной инициации и фиксированной инициации интервала [0.0001 - 0.0008] идентичны, а увеличение порядка значений инициации ухудшает результат относительно рандомной.

На всякий случай продолжим и еще раз уменьшим на 10.

Видно, что результат такой же - рандомная инициация дает те же результаты, что и фиксированная, или лучше.

Совсем для ясности возьмем другие соотношения количества нейронов и размера батча.

И снова результат тот же - рандомная инициация дает те же результаты, что и фиксированная, или лучше.

Выводы

Неожиданно для себя я убедился, что рандомная инициация (по крайней мере в случае FNN c 1 скрытым слоем) дает те же результаты, что и фиксированная, или даже лучше, и это не случайно, а на нескольких запусках, то есть градиентным алгоритмам все равно откуда начинать, главное, чтобы не слишком из далека и хватило эпох.

До следующего уровня понимания проблемы для себя я этот вопрос временно закрыл - инициация рандомная, и больше нечего об этом беспокоиться.

Примечания

Если замечены грубые ошибки, которые могут существенно изменить результаты эксперимента, то прошу указать в комментариях. И, наоборот, если в целом рассуждения и ход эксперимента видятся корректными, то также прошу указать в комментариях.