14.06.2023 08:00
alexlyk314 3 2500 Источник

Посмотрите на серию фигур из точек:

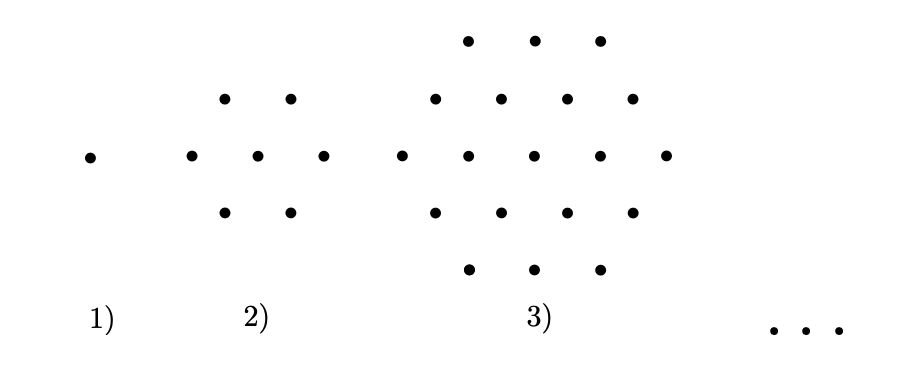
Назовём эти фигуры гексами (hex значит шесть). Первый гекс состоит из одной точки, второй — из семи точек; каждый следующий гекс получается из предыдущего добавлением одного слоя точек.

Вопрос: сколько всего точек на первых n гексах?

Сосчитаем ответ при малых n: на первых двух гексах 8 точек, на третьем -19, поэтому на первых трёх - 27. Заметим, что 8=2^3 и 27=3^3. Хм... Просто совпадение? Посмотрим, сколько точек на 4-м гексе. На его внешнем слое будет 6\cdot 3=18 точек. Плюс внутри него расположен третий гекс из 19 точек. Итого, 19+18=37 точек. Значит, всего на первых четырёх гексах 27+37=64 точки. А 64=4^3 - закономерность подтверждается. Правда ли, что на первых n гексах всегда n^3 точек? Выведем это несколькими методами.

I МЕТОД: ИНДУКЦИЯ. При n=1 утверждение верно (база). Предположим, что на первых n-1 гексах ровно (n-1)^3 точек, и докажем, что на первых n гексах ровно n^3 точек. Это равносильно тому, что число точек на n-м гексе равно

n^3-(n-1)^3=3n^2-3n+1. \;\;\;\;\;\;\; (1)

Чтобы в этом убедиться, разобьём n-й гекс на n "концентрических" слоёв: первый слой - центр из одной точки, на втором слое 6 точек, на третьем - 6\cdot 2, \ldots, на n-м - 6(n-1). Итого, число точек на n-м гексе равно

1+6(1+2+\ldots+n-1)=1+6\cdot \dfrac{n(n-1)}{2}=3n^2-3n+1,

что и требовалось.

II МЕТОД: СУММИРОВАНИЕ. Рассуждать по индукции можно, когда у нас уже есть гипотеза, какой будет ответ. Допустим, у нас такой гипотезы (про n^3) не было. Тогда мы бы просто сосчитали, сколько точек на k-м гексе (как выше), и просуммировали по k=1,\ldots,n:

\sum_{k=1}^n (3k^2-3k+1)=3\sum_{k=1}^n k^2-3\sum_{k=1}^n k + n. \;\;\;\;\;\;\; (2)

Формулу для суммы квадратов можно найти в справочнике:

1^2+2^2+\ldots+n^2=\dfrac{n(n+1)(2n+1)}{6}. \;\;\;\;\;\;\; (3)

Подставив эти выражения в вычисляемую сумму, после преобразований получим n^3. Но было бы здорово всё-таки пролить свет на формулу для суммы квадратов. Оказывается, концептуальный путь начинается с формулы (1). Проведём вывод формулы (3) в духе одной из главных теорем анализа - формулы Ньютона-Лейбница:

\int_a^b F'(x)dx=F(b)-F(a).

Её дискретный аналог тривиален. Интегрирование заменяем на суммирование, а производную --- на разность. Именно, для любой последовательности a_1,\ldots,a_n имеем:

(a_n-a_{n-1})+(a_{n-1}-a_{n-2})+\ldots+(a_3-a_2)+(a_2-a_1)=a_n-a_1.

Применим эту нехитрую идею к последовательности a_n=n^3:

\begin{align*} n^3-(n-1)^3=3n^2-3n+1,\\ \ldots\ \\ 2^3-1^3=3 * 2^2-3 * 2+1,\\ 1^3-0^3=3 * 1^3-3 * 1+1. \end{align*}

Сложив числа в левой части, получим n^3 (остальные члены сократятся, а 0^3=0).

В правой же части получим не что иное, как (2). Мы решили задачу о гексах, а заодно из неё вывели формулу (3): зная, что выражение (2) равно n^3, легко выразить из него

\sum_{k=1}^{n} k^2.

III МЕТОД: ГЕОМЕТРИЧЕСКИЙ. В качестве "вишенки на торте" покажем геометрическую интерпретацию сказанного выше. Третья степень неслучайно называется кубом, подобно тому, как вторая степень называется квадратом. Так, формула суммы первых нечётных натуральных чисел

1+3+5+\ldots+(2n-1)=n^2

имеет простой геометрический смысл: вкладывая уголки

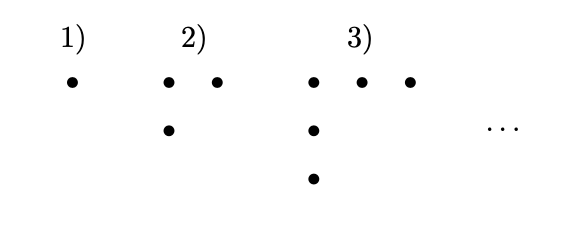
из 1, 3, 5, ... точек друг в друга как матрёшки, сложим квадрат. Оказывается, нечто аналогичное происходит и с гексами! Взгляните:

Таким образом, n-й гекс можно воспринимать как видимую часть поверхности куба n\times n\times n под соответствующим углом зрения. Например, на втором гексе вы видите куб без одной вершины - её не видно, и можно считать, что это как раз точка на первом гексе. Вообще, все эти n слоёв вкладываются друг в друга, образуя полный куб с ребром из n точек.

Автор: Андрей Канунников, к. ф.-м. н., мехмат МГУ, преподаватель ШАД Хелпер

Комментарии (3)


  1. Mavolio-Bent
    14.06.2023 09:24
    #25648892

    Чтобы в этом убедиться, разобьём n-й гекс на n "концентрических" слоёв: первый слой - центр из одной точки, на втором слое 6 точек, на третьем - 6\cdot 2, \ldots, на n-м - 6(n-1). Итого, число точек на n-м гексе равно

    Это утверждение, конечно, верно, но хотелось бы увидеть его обоснование.


  1. MasterMentor
    14.06.2023 09:24
    #25649020
    +1

    ИМХО все методы «доказательства» – жульничество: подгон нехитрых алгебраических формул под результат.
    Аргументирую.

    Вы сообщаете: «каждый следующий гекс получается из предыдущего добавлением одного слоя точек»

    По каким правилам «строятся» т.н. «слои»? что это за объекты?
    Об этом ничего не сказано. А правила получения множества этих объектов далеко не очевидны.
    Вы начинаете комбинировать множество именно геометрических (пространственных) объектов, которые на каждом «шаге» построения сохраняют следующие инварианты:
    а) количество углов у полученных фигур, начиная со второй, сохраняется и равно 6-ти
    б) периметр т.н. «слоя» (что и определяет количество точек на нем) выбирают так, что расстояния между «угловыми» точками периметров каждых прилегающих друг к другу «слоев» – неизменны, так же неизменны и равны расстояния между точками на всех периметрах (без условия б) – все ломается)

    Очевидно, что изучение свойств геометрических (пространственных) объектов следует вести через использование аппарата геометрии (ввод метрик, выделение инвариантов, анализ движений, итд.) с выходом в алгебру (алгебры) там, где это необходимо.

    В статье же сделан подбор алгебраических формул, под конкретный случай (ряд). Это не объясняет и не доказывает существование закономерности. Это лишь тождество вида «А = А».


  1. m03r
    14.06.2023 09:24
    #25652340

    Жаль, что автор не упомянул о фигурных числах вообще, хотя этим ещё античные математики занимались. По поводу «гексов» даже в русской вики есть отдельная статья.