Всем привет! Меня зовут Сакович Руслан, я занимаюсь корпоративным риск-моделированием, и сегодня расскажу о построении скоринговых моделей. Эти модели позволяют оценивать кредитные риски и являются крайне важными в деятельности банка. К ним предъявляются высокие требования в плане точности, стабильности и интерпретируемости результатов, поэтому в основном мы не можем использовать методы «черные ящики» (как например бустинги или нейросети), и обычно вынуждены пользоваться логистической регрессией. Сам по себе метод логистической регрессии довольно простой с точки зрения математики, однако для построения хорошей модели он требует тщательной предварительной обработки и энкодинга исходных данных, а также последующего довольно трудоемкого отбора переменных в модель. Причем стандартные библиотеки вообще не предоставляют возможности построения хоть какой-нибудь адекватной модели прямо из коробки. Мы решили стандартизировать весь процесс разработки скоринговых моделей, собрали используемые нами алгоритмы и объединили в библиотеку vtb_scorekit.
Самый простой вариант использования этой библиотеки – это метод LogisticRegressionModel.auto_logreg() для автоматического построения модели:
from vtb_scorekit.model import LogisticRegressionModel
lr = LogisticRegressionModel()
lr.auto_logreg(df, # ДатаФрейм с данными
target='Survived', # целевая переменная
result_folder='titanic_auto', # папка, в которую будут сохраняться все результаты работы
n_jobs=4, # кол-во используемых рабочих процессов
)Нам достаточно задать датафрейм, целевую переменную, папку для сохранения результатов и кол-во используемых для расчетов рабочих процессов, а на выходе мы получим готовую модель. Даже список переменных можно не задавать, он будет определен автоматически.
Основное же предназначение библиотеки – проведение всего пайплайна разработки с контролем результатов и возможностью внесения ручных корректировок при необходимости после каждого шага. Вообще ручные корректировки являются довольной важной частью интерпретируемых моделей, т.к. часто в угоду бизнес-логике приходится отклоняться от статистических решений, и здесь этому уделено отдельное внимание.
К ключевым особенностям можно отнести высокую скорость работы, которая достигается хорошей оптимизацией на уровне алгоритмов и использованием параллельных вычислений на разных ядрах. Ниже на графике показана зависимость времени построения модели в автоматическом режиме в минутах от кол-ва используемых ядер процессора на выборке из 160 000 записей и 280 переменных. Как видно, время сокращается со 180 мин на 1 процессоре до примерно 10 мин на 24 процессорах, что дает возможность нам достаточно быстро обрабатывать даже огромные датасеты, просто используя большое кол-во ядер кластера.
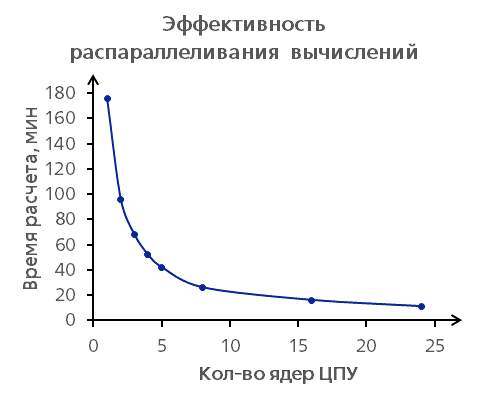
Также здесь можно отметить, что фреймворк дает возможность автоматически проверять стабильность факторов и модели в целом бутстрэпом в процессе разработки и затем провалидировать финальную модель.
Теперь пройдемся подробнее по всему процессу разработки модели. Для примера будем использовать известный датасет титаник, где нам нужно спрогнозировать вероятность выживания в кораблекрушении.
Анализ исходных данных
Для начала посмотрим на сами наши исходные данные:
import pandas as pd
df = pd.read_csv('data/train_titanic.csv')
df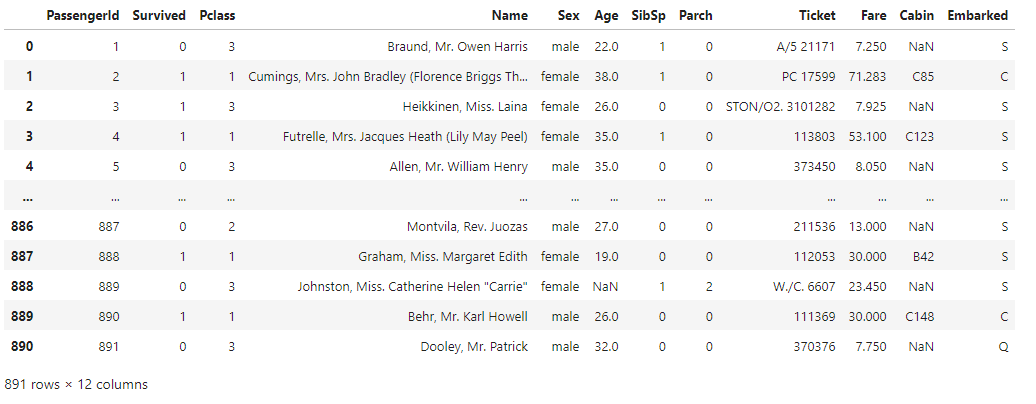
Здесь мы видим совсем небольшой датасет с 891 строкой и 12 полями. Для начала работы с ним мы создадим объект класса DataSamples, в котором будет храниться наш датасет и вся необходимая информация о нем:
from vtb_scorekit.data import DataSamples
ds = DataSamples(samples={'Train': df}, # выборка для разработки. Задается в виде словаря {название_сэмпла: датафрейм}
target='Survived', # целевая переменная
id_column='PassengerId', # уникальный в рамках среза айди наблюдения
result_folder='titanic', # папка, в которую будут сохраняться все результаты работы с этим ДатаСэмплом
feature_descriptions=pd.read_excel('data/titanic_description.xlsx', index_col=0), # датафрейм с описанием переменных
features=None, # список переменных
cat_columns=None, # список категориальных переменных
special_bins=None, # словарь вида {название бина: значение}, каждое из значений которого помещается в отдельный бин
n_jobs=4, # кол-во используемых рабочих процессов
random_state=0, # сид для генератора случайных чисел
samples_split={'test_size': 0.2}, # словарь с параметрами для вызова метода self.samples_split()
bootstrap_split={'bootstrap_part': 1.5}, # словарь с параметрами для вызова метода self.bootstrap_split()
)Нам нужно задать саму выборку, целевую переменную и папку для сохранения результатов. Далее мы можем подготовить и указать датафрейм с описанием наших переменных. В этом случае эти описания будут подтягиваться ко всем графикам и отчетам и нам будет гораздо удобнее с ними работать. Список переменных и категориальных переменных мы можем как задать сами, так и оставить на автоопределение. Также здесь можно задать параметры разбиения и параметры для создания бутстрэп сэмплов, которые потом будут использоваться для проверок стабильности и расчета доверительных интервалов.
Этот класс сам по себе является довольно мощным инструментом для анализа данных и может использоваться совершенно независимо от остального функционала фреймворка. С помощью его методов можно:
Генерировать новые переменные с отсеиванием неудачных на лету, чтобы не захламлять датасет бесполезным мусором.
Разбивать выборки на сэмплы, которое гораздо более функционально, чем стандартный train_test_split из склерна – в нем мы может делать сплит как out-of-sample, так и out-of-time и использовать стратификацию по набору полей.
Посчитать статистику по сэмплам.
Построить распределения переменных и распределение целевой переменной вдоль остальных переменных.
Рассчитать множество различных метрик и провести стат тесты.
В первую очередь, для того, чтобы понять, насколько хорошо наши переменные предсказывают целевую переменную, мы можем посмотреть на однофакторные метрики Gini. Сделать это можно вызвав метод calc_gini():
ds.calc_gini(features=None, prebinning=True, add_description=True)
Здесь мы сразу получаем однофакторные Gini всех переменных по всем доступным сэмплам, а также среднее и стандартное отклонение на бутстрэп сэмплах. Т.к. в данных присутствуют пропуски, а переменные «Sex» и «Embarked» вообще являются не числовыми, то необходимо использовать опцию prebinning, с которой перед расчетом будет выполнен предварительный быстрый биннинг переменных.
Однофакторный анализ
После того, как мы сформировали выборки и посмотрели на данные, можно приступать к энкодингу переменных и однофакторному анализу. Для логистической регрессии это ключевой этап, т.к. качество модели очень сильно зависит от того, насколько хорошо мы преобразовали наши данные. Для риск моделей общепринятым стандартом является WOE-трансформация, поэтому на данный момент только она и доступна для использования во фреймворке, но в ближайших планах у нас есть добавление и других энкодеров.
Для начала нам необходимо создать объект класса WOE:
from vtb_scorekit.woe import WOE
bn = WOE(ds, # ДатаСэмпл
scorecard=None, # путь к эксель файлу или датафрейм с готовыми биннингами для импорта
round_digits=3, # округление границ бинов до этого числа знаков после запятой
rounding_migration_coef=0.005, # максимально допустимая доля наблюдений для миграции между бинами при округлении
simple=True, # если True, то расчет WOE происходит на трэйн сэмпле, иначе берется среднее значение по фолдам
n_folds=5, # кол-во фолдов для расчета WOE при simple=False
woe_adjust=0.5, # корректировочный параметр для расчета EventRate_i в бине i
alpha=0, # коэффициент регуляризации для расчета WOE
alpha_range=None, # если alpha=None, то подбирается оптимальное значение alpha из диапазона alpha_range
alpha_scoring='neg_log_loss', # метрика, используемая для оптимизации alpha
alpha_best_criterion='min', # 'min' - минимизация метрики alpha_scoring, 'max' - максимизация метрики
missing_process='max_or_separate', # способ обработки пустых значений
missing_min_part=0.01, # минимальная доля пустых значений для выделения отдельного бина
others='missing_or_max', # Способ обработки значений, не попавших в биннинг
opposite_sign_to_others=True, # В случае, когда непрерывная переменная на выборке для разработки имеет только один знак,
# то все значения с противоположным знаком относить к others
)При его инициализации нужно задать параметры расчета WOE в бинах. Здесь мы используем обобщенную формулу с коэффициентом регуляризации alpha и корректировочной поправкой woe_adjust:
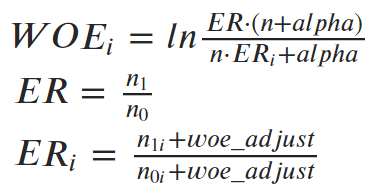
где n - общее кол-во наблюдений в выборке, n1 - общее кол-во наблюдений класса 1, n0 - общее кол-во наблюдений класса 0, n1i - кол-во наблюдений класса 1 в бине i, n0i - кол-во наблюдений класса 0 в бине i. Параметр alpha мы можем как задать самостоятельно, так и вычислять ее оптимальное значение для каждой переменной автоматически. Также здесь можно определить будем ли мы рассчитывать WOE целиком на всей обучающей выборке, или разобьём ее на n фолдов, посчитаем отдельно на каждом и усредним. И еще нам нужно указать способ обработки пустых значений и значений, не попавших в биннинг. Как правило разработчики не задумываются каким образом модель на применении будет обрабатывать значения, которых не было в выборке для разработки. Например, на разработке у было 100% заполненность переменной, а на применении там появились пропуски, или строковую переменную записали с ошибкой, что с этим делать? Часто в пакеты зашиты какие-то дефолтные методы обработки, они сами там как-то там работают и ладно, при разработке моделей это обычно никак не обсуждается и нигде не фиксируется. Для WOE-трансформаций в качестве такого дефолтного метода используется как правило присваивание таким значениям наименьшего WOE в бинах, но в общем случае это подходит только для негативных целевых событий, таких как, например, дефолт или мошенничество, а если у нас целевое событие позитивное, как например, здесь в титанике – спасение в кораблекрушении, то наименьшее WOE соответствует наибольшей вероятности спастись, а худшим значением является наоборот наибольшее WOE. Поэтому здесь мы добавили возможность прямо указать каким образом нужно обрабатывать такие ситуации, и в скоркарту добавили бин others в явном виде.
В качестве ключевых возможностей нашего фреймворка в однофакторном анализе можно выделить проверку биннинга на стабильность и переобучение. Т.к. при WOE-трансформации мы используем информацию о целевой переменной, то здесь мы можем переобучиться уже на этом этапе, поэтому крайне важно контролировать качество биннинга, иначе просто невозможно будет сделать хорошую модель.
Для поиска оптимального биннинга используется метод WOE.auto_fit():
bn.auto_fit(features=None, # список переменных для обработки
autofit_folder='auto_fit', # название папки, в которую будут сохранены результаты автобиннинга
# --- Метод биннинга ---
method='opt', # 'tree' - биннинг деревом, 'opt' - биннинг библиотекой optbinning
max_n_bins=10, # максимальное кол-во бинов
min_bin_size=0.05, # минимальное число (доля) наблюдений в каждом листе дерева
# --- Параметры биннинга для метода 'tree' ---
criterion='entropy', # критерий расщепления. Варианты значений: 'entropy', 'gini', 'log_loss'
scoring='neg_log_loss', # метрика для оптимизации
max_depth=5, # максимальная глубина дерева
#--- Параметры биннинга для метода 'opt' ---
solver='cp', # солвер для оптимизации биннинга:
# 'cp' - constrained programming
# 'mip' - mixed-integer programming
# 'ls' - LocalSorver
divergence='iv', # метрика для максимизации:
# 'iv' - Information Value,
# 'js' - Jensen-Shannon,
# 'hellinger' - Hellinger divergence,
# 'triangular' - triangular discrimination
# --- Параметры проверок ---
WOEM_on=True, # флаг проверки на разницу WOE между соседними группами
WOEM_woe_threshold=0.1, # если дельта WOE между соседними группами меньше этого значения, то группы объединяются
WOEM_with_missing=False, # должна ли выполняться проверка для бина с пустыми значениями
SM_on=False, # проверка на размер бина
SM_target_threshold=10, # минимальное кол-во (доля) наблюдений с целевым событием в бине
SM_size_threshold=100, # минимальное кол-во (доля) наблюдений в бине
BL_on=True, # флаг проверки на бизнес-логику
BL_allow_Vlogic_to_increase_gini=10, # разрешить V-образную бизнес-логику для увеличения джини относительного монотонной
G_on=True, # флаг проверки на джини
G_gini_threshold=5, # минимальное допустимое джини переменной
G_with_test=True, # также проверять джини на остальных доступных сэмплах
G_gini_decrease_threshold=0.5, # допустимое относительное уменьшение джини на всех сэмплах относительно трэйна
G_gini_increase_restrict=False, # также ограничение действует и на увеличение джини
WOEO_on=True, # флаг проверки на сохранения порядка WOE на бутстрэп-сэмплах
WOEO_analytic=False, # всегда считать доверительные интервалы аналитически
WOEO_all_samples=True, # проверять сохранение тренда WOE на всех сэмплах относительно трейна
pvalue=0.05, # уровень значимости для оценки доверительных интервалов
# --- Пространство параметров ---
params_space={'method': ['opt', 'tree'], # пространство параметров, с которыми будут выполнены автобиннинги.
'criterion': ['entropy', 'gini']}, # Задается в виде словаря {параметр: список значений}
woe_best_samples=None, # список сэмплов, джини которых будет учитываться при выборе лучшего биннинга
# --- Кросс переменные ---
cross_features_first_level=None,# список переменных первого уровня для которых будут искаться лучшие кросс пары
cross_num_second_level=0 # кол-во кросс пар, рассматриваемых для каждой переменной первого уровня
)Алгоритм работы этого метода следующий:
Ищется разбиение на максимальное кол-во бинов. Для этого может использоваться либо наш собственный алгоритм, основанный на деревьях, либо библиотека optbinning.
-
Далее в найденном биннинге проводятся проверки
на тренд WOE — он может быть либо монотонным, либо V (или /\)‑образным, но во втором случае Gini переменной должно быть выше относительно монотонного тренда на заданную в параметрах величину. Такая дополнительная проверка позволяет исключить случайные отклонения от монотонности в трендах
стабильность тренда WOE — тренд должен сохраняться на всех тестовых сэмплах, и доверительные интервалы WOE в соседних бинах не должны пересекаться
стабильность Gini — Gini на всех тестовых сэмплах не должно сильно отличаться относительно обучающей выборки и все значения должны попадать в доверительные интервалы, рассчитанные бутстрэпом.
Если хотя бы одна проверка не пройдена, то максимальное число бинов уменьшается, и процедура повторяется до тех пор, пока мы не получим стабильный биннинг, удовлетворяющий всем заданным критериям.
После этого мы можем заново провести поиск уже с другим набором параметров, например, другим методом или другим критерием расщепления дерева, а затем из всех найденных стабильных биннингов автоматически выбирается оптимальный с наилучшим Gini.
В результате всех этих расчетов мы получаем и тестируем десятки (а иногда и сотни) биннингов для каждой переменной и выбираем из них лучший. Благодаря тому, что расчет каждой переменной идет полностью независимо от остальных, можно проводить все эти вычисления параллельно и, выделив большое число ядер для расчета, получать результат достаточно быстро.
В интерпретируемых моделях крайне важно иметь возможность анализировать логику работы всех переменных и при необходимости вносить корректировки в биннинг. Для этих целей мы собрали всю необходимую информацию для такого анализа и поместили ее на график.
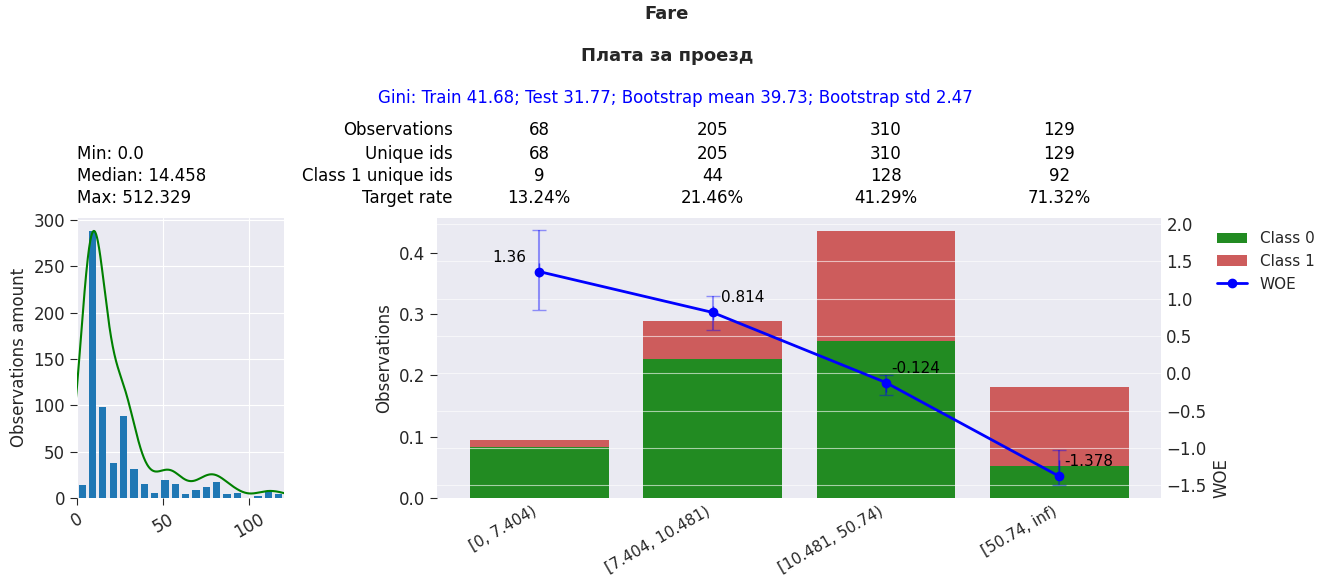
Например, здесь приведен такой график для биннинга переменной «Fare». Слева показано распределение исходной переменной, ее минимальное, медианное и максимальное значения, а справа показаны бины – по оси Х отложены диапазоны значений бинов, по оси Y доля наблюдений, значения и доверительные интервалы WOE в этих бинах. Тут, например, сразу видно, что с ростом платы за проезд у нас достаточно быстро падает WOE и соответственно растет таргет рейт, т.е. доля выживших, и наглядно понятно каким образом эта переменная разделяет выборку. Если необходимо, то с помощью дополнительных методов можно менять границы, разбивать и объединять бины, и наблюдать за изменениями на перестроившихся графиках.
Также можно обратить внимание, что у нас не было отрицательных значений на разработке, поэтому биннинг мы начинаем не с минус бесконечности, как это обычно принято, а с нуля, и если вдруг будут пустые или отрицательные значения на применении, то они уйдут в бакет others с максимальным значением WOE. Кроме того, мы можем изменять значения WOE в нем как нам угодно, и таким образом при помощи этого бакета организовывать контроль качества входных данных модели на применении на уровне скоркарты:
group |
values |
woe |
n |
n1 |
0 |
[0, 7.404] |
1.36 |
68 |
9 |
1 |
[7.404, 10.481] |
0.814 |
205 |
44 |
2 |
[10.481, 50.74] |
-0.124 |
310 |
128 |
3 |
[50.74, inf] |
-1.378 |
129 |
92 |
others |
all others |
1.36 |
Скоркарта переменной «Fare»
Многофакторный анализ
После того, как мы закончили с однофакторным анализом, можно приступать к многофакторному. Для этих целей у нас есть класс LogisticRegressionModel:
from vtb_scorekit.model import LogisticRegressionModel
from sklearn.linear_model import LogisticRegression
lr = LogisticRegressionModel(clf=LogisticRegression(), # классификатор модели
ds=ds, # ДатаСэмпл
transformer=bn, # объект класса WOE для трансформации факторов
name='titanic_model' # название модели
) Здесь у нас есть возможность выполнить весь многофакторный анализ вызвав один метод mfa():
lr.mfa(features=None, # исходный список переменных для МФА
hold=None, # список переменных, которые обязательно должны войти в модель
gini_threshold=5, # трешхолд по джини для этапа 1
psi_threshold=0.25, # трешхолд по PSI для этапа 1
corr_method='pearson', # метод расчета корреляций для этапа 2
corr_threshold=0.80, # граница по коэффициенту корреляции для этапа 2
drop_with_most_correlations=False, # вариант исключения факторов в корреляционном анализе для этапа 2
drop_corr_iteratively=False, # исключение коррелирующих факторов не на отдельном этапе 2, а итеративно в процессе этапа 3
selection_type='stepwise', # тип отбора для этапа 3
pvalue_threshold=0.05, # граница по p-value для этапа 3
pvalue_priority=False, # вариант определения лучшего фактора для этапа 3
scoring='gini', # максимизируемая метрика для этапа 3
score_delta=0.1, # минимальный прирост метрики для этапа 3
drop_positive_coefs=True, # флаг для выполнения этапа 4
# --- Кросс переменные ---
crosses_simple=False, # True - после трансформации кросс-переменные учавствут в отборе наравне со всеми переменными
# False - сначала выполняется отбор только на основных переменных, затем в модель добавляются
# по тем же правилам кросс переменные, но не более, чем crosses_max_num штук
crosses_max_num=3, # максимальное кол-во кросс переменных в модели. учитывается только при crosses_simple=False
# --- Отчет ---
result_file='mfa.xlsx', # файл, в который будут сохраняться результаты мфа
metrics=['wald', 'ks', 'vif'], # список метрик/тестов, результы расчета которых должны быть включены в отчет
)Весь многофакторный анализ проводится в 4 этапа:
Сначала будут отсечены слабые и не стабильные факторы по заданным трешхолдам Gini и PSI факторов
Затем будет проведен корреляционный анализ и исключены коррелирующие факторы, либо как альтернатива этот шаг может быть пропущен, а коррелирующие факторы могут исключаться динамически по мере отбора факторов в модель. Эта опция обычно позволяет получить немного более сильную модель, но вычислительные затраты возрастают на порядок.
На третьем этапе проводится итерационный отбор факторов, который может отбирать переменные как для максимизации заданной метрики, так и по p-value переменных.
В самом конце исключаются малозначимые факторы и вошедшие в модель со знаком, противоречащим бизнес-логике.
Все проведенные операции и результирующая модель записываются в отчет в эксель файле, и мы потом можем детально проанализировать весь процесс отбора, и при необходимости сделать замену факторов. Итоговая сводная таблица по собранной модели из отчета показана снизу – тут приведены джини всех вошедших факторов и модели в целом, коэффициенты факторов вместе со стандартными ошибками, а также значения метрик и тестов, которые мы определили в параметрах:
После сборки модели мы можем провести ее калибровку и выполнить автоматически базовую валидацию, прогнав ряд тестов и раскрасив их результаты в зелено-желто-красные сигналы.
А в самом конце разработки после того, как финальная версия модели собрана и согласована, мы можем сгенерировать хардкод для ее применения вызвав метод LogisticRegressionModel.to_py():
lr.to_py()В данном примере он вернет следующий код:
import pandas as pd
import numpy as np
def scoring(df, score_field='score', pd_field='pd', scale_field=None):
"""
Функция скоринга выборки
Arguments:
df: [pd.DataFrame] входной ДатаФрейм, должен содержать все нетрансформированные переменные модели
score_field: [str] поле, в которое должен быть записан посчитанный скор
pd_field: [str] поле, в которое должен быть записан посчитанный PD
scale_field: [str] поле, в которое должен быть записан посчитанный грейд
Returns:
df: [pd.DataFrame] выходной ДатаФрейм с добавленными полями трансформированных переменных, скоров, PD и грейда
"""
df['SibSp_WOE'] = np.where(df['SibSp'].isin([3, 4, 5, 8]), 1.165,
np.where(df['SibSp'].isin([0]), 0.18,
np.where(df['SibSp'].isin([1, 2]), -0.635,
1.165)))
df['Sex_WOE'] = np.where(df['Sex'].isin(['male']), 0.993,
np.where(df['Sex'].isin(['female']), -1.542,
0.993))
df['Fare_WOE'] = np.where((df['Fare'] >= 0) & (df['Fare'] < 7.404), 1.36,
np.where((df['Fare'] >= 7.404) & (df['Fare'] < 10.481), 0.814,
np.where((df['Fare'] >= 10.481) & (df['Fare'] < 50.74), -0.124,
np.where((df['Fare'] >= 50.74), -1.378,
1.36))))
df['Age_WOE'] = np.where(df['Age'].isnull(), 0.425,
np.where((df['Age'] >= 0) & (df['Age'] < 6.5), -0.958,
np.where((df['Age'] >= 6.5), -0.042,
0.425)))
df[score_field] = -0.488 + (-0.623) * df['SibSp_WOE'] + (-0.945) * df['Sex_WOE'] + (-0.772) * df['Fare_WOE'] + (-0.815) * df['Age_WOE']
df[pd_field] = 1 / (1 + np.exp(-df[score_field]))
return df
df = scoring(df, score_field='score', pd_field='pd', scale_field=None)В нем создается функция scoring(), которая проводит трансформацию факторов и рассчитывает итоговый скор. Использование модели на применении при помощи такого кода гораздо удобнее стандартного подхода с загрузкой биннинга и модели из внешних файлов, т.к. здесь мы не привязаны ни к какой библиотеке, используются только стандартные pandas и numpy, и мы избегаем ошибок, когда обновился, например, код исполнения, но забыли обновить сами файлы модели или наоборот, т.к. здесь у нас вся необходимая информация хранится в коде скрипта.
Заключение
Использование этого фреймворка предоставляет возможность провести полный цикл разработки модели от анализа исходных данных до валидации и подготовки кода для применения. Такой подход обеспечивает стандартизацию и структурировать процесса разработки, сокращает риск операционных ошибок, а также дает воспроизводимость результатов.
На данный момент фрейморк у нас используется полгода, и за это время с его помощью было разработано 30 моделей, при этом по нашим оценкам ускорение разработки произошло в 3-4 раза.
В этой статье показан лишь базовый функционал фреймворка, описание всех методов его классов и больше примеров можно посмотреть тут.

