Конфиденциальность и безопасность в сети никогда не были актуальней, чем сегодня. Компании, госслужащие и частные лица сталкиваются со всё более высокими рисками, чем когда-либо прежде. Киберпреступность, злоупотребления со стороны государственных структур и банальный шпионаж процветают не только в голливудских фильмах. Финансовая информация, деанонимизация личности, коммерческие патенты или просто конфиденциальные сообщения, — каждому есть что терять, даже если ему нечего скрывать. Одним из самых популярных вариантов решения этого вопроса является использование шифрования. За последние годы PGP, а затем и OpenPGP стали стандартом почти для всех подписанных или зашифрованных электронных писем в мире.

Криптосистема Эль-Гамаля является одной из самых старых и наиболее известных схем шифрования с открытым ключом. Эта ассиметричная система основана на обмене ключами Диффи-Хеллмана. До начала 2000 годов она была практически самой распространённой системой благодаря своей эффективности и необременённости патентным правом. Наиболее заметное использование схемы относится к реализации сквозной зашифрованной электронной почты в стандарте OpenPGP. Безопасность схемы полностью зависит от сложности факторизации дискретных логарифмических задач, в которых сложно вычислить дискретные логарифмы над конечными полями с помощью атак грубой силы или статистических атак. Что удивительно, учитывая возраст схемы шифрования и простоту реализации алгоритмов, можно было бы предположить, что используемые спецификации отлажены и строги, однако на деле всё совсем не так. Существует множество различных вариантов реализации системы, особенности которых зависят только от желания разработчиков программных продуктов. Как результат, периодически всплывают всё новые уязвимости, которые ведут к перехвату зашифрованной информации со всеми вытекающими отсюда последствиями. Например, вполне реальна ситуация, когда две реализации схемы шифрования, взаимодействуя друг с другом с разными конфигурациями параметров, в лучшем случае, с точки зрения безопасности, могут быть несовместимы, а в худшем — будут просто небезопасны.

За последние несколько лет появилось несколько исследований стойкости шифрования OpenPGP к взлому. Большая часть работ эксплуатирует оценку утечек по побочным каналам, которые можно использовать в некоторых сценариях атак (например, когда хакер и жертва находятся в одном облачном узле). Результаты экспертиз неутешительны. Вне зависимости от различий конфигураций параметров, используемых в реализациях разных поставщиков, вероятность эффективных атак очень велика. При некоторых комбинациях используемого программного обеспечения отправителя и получателя безопасность вообще носит чисто символический характер, и для взлома достаточно самых скромных ресурсов и минимальных математических способностей. Так называемые «крепкие ворота с мощным замком и дырявым забором».

Для успешной атаки потребуется перехватить часть зашифрованных текстов (например, путем анализа трафика общедоступной сети, для защиты которой в общем-то и предназначен OpenPGP). Такие атаки называются кросс-конфигурационными атаками. Конечно, не всё так плохо, потому что безопасность шифрования по Эль-Гамалю зависит от деталей реализации. В некоторых случаях существует возможность прямого взлома зашифрованных текстов, другие вскрываются при наличии дополнительных утечек по сторонним каналам, но есть и безопасные варианты (по крайней мере, на текущий момент). Чтобы оценить стойкость шифрования по Эль-Гамалю, нужно для начала рассмотреть совокупность различных интерпретаций OpenPGP, использующихся на практике.

Результаты работы по доскональному изучению стандарта OpenPGP (RFC4880), проверки исходного кода ряда библиотек, реализующих OpenPGP, и исследование множества ключей настораживают. В некоторых вариантах успешно реализована атака против 2048-битных ключей, битовая длина которых сегодня считается практически безопасной.

Со времени появления схемы шифрования Эль-Гамаля ряд исследований выявил проблемы безопасности как в реализации, так и на уровне спецификации. В текущем виде в OpenPGP схема используется исключительно для передачи ключей.

Общая форма шифрования Эль-Гамаля

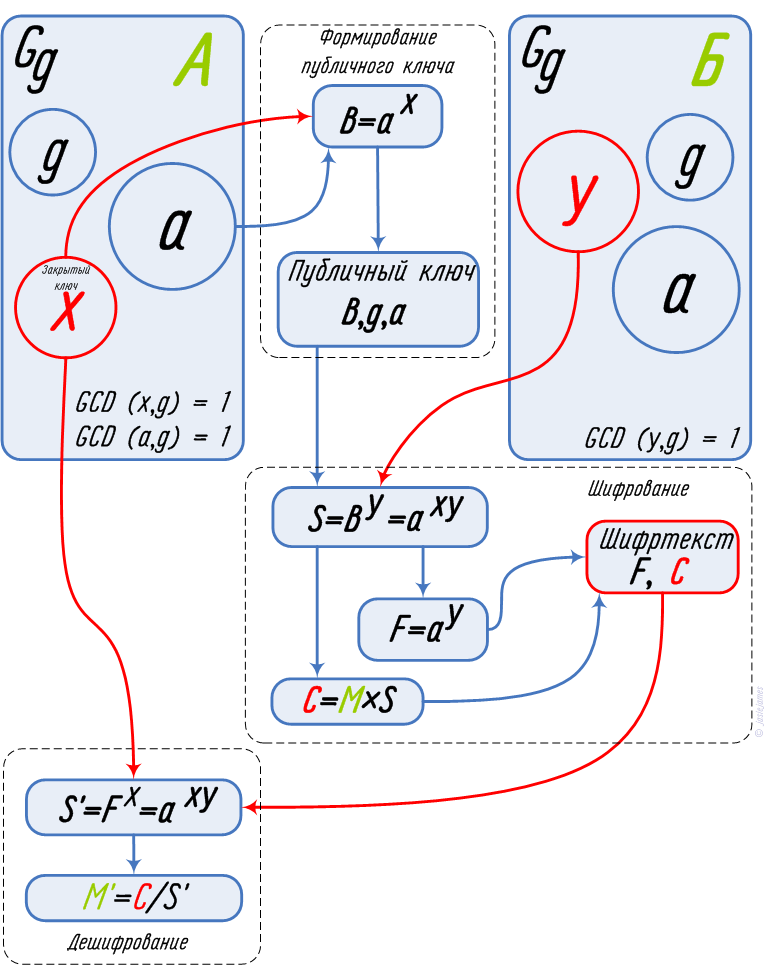
Для реализации схемы используется сложность вычисления дискретного логарифма в циклической группе. Обобщённая схема показана на рисунке. 

Корреспондент А выбирает достаточно большое число g, порождающее циклическую группу G_g. Из множества G_g выбирается такое число x, чтобы соблюдалось условие GCD(x,g)=1. Число x — закрытый ключ. Далее формируется публичный ключ (B,g,a), где a — число из множества G_g, GCD(a,g)=1, B=a^x. Корреспондент Б шифрует сообщение M. Для этого из множества G_g выбирается произвольное число y при GCD(y,g)=1 (в некотором роде сеансовый множитель). Вычисляется гамма S, S=B^y=a^xy и дополнительное число F=a^y. Получаем и передаём шифртекст (F,C), где C=M×S.

Для дешифровки корреспондент А вычисляет гамму S' как S'=F^x=a^xy, по известному только ему закрытому ключу x и расшифровывает текст M'=C/S'.

Для создания рабочего и безопасного экземпляра схемы должны быть уточнены следующие детали: 

• Какую группу G_g следует использовать?

• Как выбирается порождающее число g?

• Согласно каким распределениям выбираются числа из группы? 

Существует несколько конфигураций параметров, общим для которых является то, что G_g является циклической группой.

Конфигурация 1

Оригинальная схема требует выбора g таким образом, чтобы оно порождало (p – 1) элемент, то есть полную группу. Числа выбираются равномерно из [1, …, p−1]. Единственное условие для p состоит в том, что (p – 1) должно иметь, по крайней мере, один большой простой делитель (для противодействия атаке Полига-Хеллмана).

Если используется эта конфигурация, любой элемент G_g может стать ключом. Однако некоторые из этих ключей будут иметь более низкий мультипликативный порядок, чем другие, то есть генерировать меньшую подгруппу и, таким образом, обещать меньшую безопасность. Для исключения опасных вариантов нужно ограничить групповые операции Эль-Гамаля подгруппой простого порядка G' ⊊ G. Действительно, если G' = g имеет простой порядок, то все его элементы обязательно имеют один и тот же порядок (за исключением нейтрального элемента). Пусть (p – 1) = (q₀ … q_n) будет разложением ord(G) на простые множители.

Поскольку p — большое простое число и, следовательно, нечётное, мы знаем, что один из этих простых множителей равен 2, и, следовательно, мы записываем (p – 1) = (2q₁ … q_n). Теперь для любого простого числа q = q_i в этом списке факторов существует подгруппа G' ⊊ G порядка q. Идея использования такой группы G' в криптографии принадлежит Шнорру. 

Конфигурация 2

Эль-Гамаль поверх групп Шнорра. Для реализации усложнённой схемы нужно выбрать большой порядок группы простых чисел q и простое число p такие, что q|(p − 1). Также выберем образующую Y такую, что Y = G , и пусть g = Y^{(p − 1)/q} и G' = g. Обратите внимание, что это подразумевает ord(G') = q. Числа x и y выбираются из [1, …, q − 1].

Эта установка удовлетворяет условию Полига-Хеллмана и гарантирует, что все нетривиальные элементы G' имеют один и тот же порядок. Далее, если q << p, поскольку показатели x, y теперь выбираются из [1, …, q − 1] вместо [1, …, p − 1], реализации этой гибридной конфигурации достаточно эффективны.

В то время как такая конфигурация устраняет риск случайного использования элементов малого порядка, злоумышленник всё же может использовать существование небольших подгрупп в активной атаке. Восстановление [x (mod t₁), x (mod t₂), …] позволяет вычислить полный показатель степени x с помощью китайской теоремы об остатках. Поскольку для каждого значения t злоумышленник должен запросить расшифровки, малые значения t являются предварительным условием эффективности атаки. Так же как и существование достаточного количества подходящих t. Следовательно, одна контрмера против атаки состоит в том, чтобы гарантировать, что число различных делителей t числа (p – 1) будет очень маленьким, а другая — сделать так, чтобы все допустимые значения t были очень большими. Следующие конфигурации формализуют эти идеи.

Конфигурация 3

Эль-Гамаль поверх безопасных простых чисел. В этом варианте реализации количество подгрупп сводится к минимуму. Выбирается большой порядок группы чисел q и простой модуль p такие, что (p – 1) = 2q, образующая Y с Y = G и пусть g = Y^{(p − 1)/q} и G' = g . Числа x и y из [1, …, q − 1], p ≈ q. Выбор g = 4 = (±2)² всегда возможен, что приводит к меньшим параметрам.

Конфигурация 4

Эль-Гамаль поверх простых чисел по Лим-Ли. В этом случае все нетривиальные подгруппы большие. Для реализации выбирается большой простой модуль p такой, что для простой факторизации (p – 1) = (2q₁ … q_n) все q_i имеют одинаковую большую битовую длину (тогда взломать DLP сложно для всех групповых порядков q_i). Образующая Y = G и пусть g = Y^(p−1)/q и G' = g. Числа x и y из [1, …, q − 1]. 

Поскольку показатели степени в конфигурации 3 снова стали большими, некоторые реализации работают с малыми x и y для повышения производительности. Конфигурация 4 поддерживает хорошую производительность без таких ухищрений. Однако параметры четвёртой конфигурации больше. При построении защищенной системы с нуля представляется целесообразным использовать один из этих двух вариантов.

Схема Эль-Гамаля в OpenPGP

OpenPGP — широко распространенный стандарт криптографии, обязывающий внедрять шифрование Эль-Гамаля (однако не рекомендуется использовать ключи менее 1024 бит). Хотя его первая версия была представлена в 1998 году, последняя официальная версия появилась в 2007 году как RFC 4880. RFC ссылается на внешние документы для спецификации криптосистемы Эль-Гамаля. В частности в Разделе 9.1 приведены две ссылки, которые в конечном итоге приводят к исходной статье Эль-Гамаля, то есть к стандартной конфигурации, описанной выше. Отметим, что разделы 5.1 и 5.5, определяющие представление в виде двоичных строк шифртекстов Эль-Гамаля, открытых и закрытых ключей, не добавляют дополнительных условий для генерации и использования ключей и шифртекстов Эль-Гамаля.

Библиотеки OpenPGP интерпретируют стандарт по-разному. Вот выводы по трём популярным из них:

Go. Предоставляет алгоритмы для шифрования и дешифрования, но не предоставляет код для генерации ключей. Сеансовый множитель y, используемый в шифровании, выбирается из [0, …, p − 1], что полностью соответствует рекомендациям.

Crypto++. Библиотека генерирует случайное простое число, выбирая для генератора наименьший квадратичный остаток, однако выбирает числа x и y из короткого интервала, размером примерно вдвое превышающего параметр безопасности. Поскольку генератор групп не является примитивным, этот параметр конфликтует с RFC4880.

gcrypt. Библиотека генерирует модуль как в конфигурации 4. Минимальный размер простых множителей q_i|(p − 1) также примерно вдвое превышает параметр безопасности. В отличие от конфигурации 4, в качестве генератора выбирается наименьшее целое число, порождающее полную группу Z^x_p. Оба числа x и y выбираются из коротких интервалов размером примерно q^3/2. В результате этот параметр конфликтует с RFC4880.

Чтобы получить полное представление об использовании схемы в OpenPGP, недостаточно взглянуть на известные библиотеки с открытым исходным кодом. Большая часть пользователей использует проприетарные или экзотические реализации, которые невозможно отследить. Чтобы решить эту проблему, был проанализирован дамп сервера открытых ключей OpenPGP.

Открытый ключ состоит из триплета (B,g,a). Одной этой информации недостаточно, чтобы с уверенностью отнести ключ к одной из конфигураций, однако частичную информацию можно вывести, попытавшись разложить (p – 1) на множители. Например, безопасные простые числа можно распознать, запустив тест на простоту на (p − 1)/2, и определить, какую группу порождает g (подгруппу простого порядка или полную группу). Для случайных простых чисел тех размеров, которые мы рассматриваем, в общем случае невозможно получить полную факторизацию (p – 1), однако частичная факторизация и тесты на остаточные значения позволяют, по крайней мере, сформулировать достоверные гипотезы о процессе генерации ключей.

Чтобы классифицировать открытые ключи, был проведен ряд манипуляций, в результате чего получились следующие цифры (учитывая, что это вычисленные на основании гипотез значения, реальные цифры могут немного отличаться):

— 69,4% ключей используют безопасные простые числа;

— 25,3% используют модули, которые, скорее всего, были сгенерированы с помощью метода Лима-Ли (конфигурация 4);

— 5,0% используют то, что в некоторых исследованиях называется «квазибезопасными простыми числами», то есть простые числа вида р = Q×q+1, где q — необычно большое простое число (в среднем в 0,988 раза больше размера p) и Q > 2;

— менее 0,3%, используют нетривиальные множители, но в этих случаях не удалось завершить факторизацию, что указывает на то, что числа были выбраны либо случайным образом, либо как в конфигурации 2.

Кросс-конфигурационные атаки

Разногласия по интерпретации стандарта OpenPGP могут вызвать сомнения в совместимости между библиотеками. Например, в гипотетической ситуации, когда Crypto++-код используется для создания пары ключей, Go-код используется для шифрования сообщения с помощью открытого ключа, а код gcrypt используется для расшифровки зашифрованного текста, необходимо прояснить вопрос, как это повлияет на конфиденциальность. Хотя в базовом сценарии эти три библиотеки теоретически могут безопасно взаимодействовать друг с другом, необходимо всё-таки оценить масштаб проблемы.

Понятно, что если (p – 1) содержит достаточно малых множителей и g порождает полную группу (например, в стандартной конфигурации применения схемы), то использование малых множителей в открытом ключе может привести к восстановлению ключа. Crypto++ использует безопасные простые числа, поэтому не подвергается риску. Хотя gcrypt генерирует (p – 1) с особенностями, он также относительно безопасен. Однако обе библиотеки используют короткие показатели степени в сеансовом ключе F, а порождающая g является частью открытого ключа, который мог быть сгенерирован другой библиотекой, возможно, соответствующей стандартной конфигурации. Анализ зарегистрированных ключей показывает, что такие открытые ключи, хотя и редко, существуют, что немедленно приводит к успешной атаке и восстановлению сообщения. Получив зашифрованный текст (a^y, M × a^xy), злоумышленник вычисляет y, использует открытый ключ для вычисления a^xy и восстанавливает открытый текст M.

То есть всякий раз, когда открытый ключ получателя определяет генератор группы, содержащей достаточное количество подгрупп малого порядка, и отправитель использует малые множители в сеансовом ключе, злоумышленник, перехватывающий сообщения, может расшифровать любое сообщение от отправителя к получателю. Точная стоимость атаки зависит от количества и размера небольших подгрупп.

Атаки с использованием побочных каналов

Условия атаки, описанные выше, не зависели от недостатков реализации, а были исключительно на совести разработчиков, придумывающих концептуальные интерпретации шифрования Эль-Гамаля, но существуют и варианты кросс-конфигурационных атак, которые основаны на слабостях реализации. Особое внимание привлекает утечка во время выполнения алгоритма модульного возведения в степень gcrypt, которое представляет собой важный компонент реализации схемы шифрования. В то же время в gcrypt предприняты явные меры для предотвращения утечки по побочным каналам (в частности, для защиты степени x).

Библиотека gcrypt реализует алгоритм возведения в степень с помощью метода скользящего окна, который является производным от базового алгоритма быстрого возведения в степень. Несмотря на встроенные меры защиты, состояние побочного канала в gcrypt может привести к полному восстановлению экспоненты. Размер окна W, используемого для возведения в степень, варьируется от 1 до 5, в зависимости от битового размера экспоненты. На первый взгляд, утечка оконного возведения в степень не кажется серьезной угрозой для среднего gcrypt закрытого ключа. Однако эта оценка обманчива по двум причинам: 

— стандартное отклонение довольно велико, и, таким образом, некоторые ключи сломать будет намного легче, чем другие;

— gcrypt считается безопасной, даже если работает с секретными ключами, сгенерированными другой библиотекой, если они являются допустимыми ключами OpenPGP, однако некоторые библиотеки генерируют секретные множители малой битовой длины, в связи с чем их ключи являются более лёгкими целями.

Возьмём за основу наиболее часто используемый размер модуля |р| = 2048. Экспоненты Crypto++ имеют длину от 1 до 226 бит, а размер используемого окна gcrypt не превышает W = 3, что приводит к средней энтропии 98,0 бит. Что еще хуже, чем ожидается. Более одного из 10 000 ключей будет иметь не более 80 битов энтропии утечки: для такого небольшого пространства поиска потребуется всего 250 модульных умножений. Таким образом атака существенной доли Crypto++ сгенерированных открытых ключей в рамках gcrypt процедуры дешифрования вполне доступна для достаточно сообразительного злоумышленника.

Итак, что в конечном остатке? Несмотря на популярность и возраст схемы шифрования Эль-Гамаля, нельзя говорить о каком-то монолитном использовании данного алгоритма. Существует несколько его разновидностей, при этом ключевой выбор остается на усмотрение поставщиков и разработчиков. Некоторые из этих вариантов создают проблемы совместимости, которые приводят к серьёзным уязвимостям.

Кросс-конфигурационные атаки практически всегда используются в связке с анализом утечек по побочным каналам. Такой комплексный подход, применяемый к несовместимым конфигурациям с точки зрения безопасности, работающим во взаимосвязанной экосистеме OpenPGP, даёт положительные результаты. На данный момент разрабатывается новая версия стандарта OpenPGP, и я надеюсь, что он станет намного безопаснее и сильнее.

НЛО прилетело и оставило здесь промокод для читателей нашего блога:
-15% на заказ любого VDS (кроме тарифа Прогрев) — HABRFIRSTVDS.