Мы ежедневно пользуемся распределёнными системами (в форме интернет-сервисов). Эти системы очень полезны, но и реализовывать их непросто, так как сети непредсказуемы. Всякий раз, когда вы передаёте сообщение по сети, предполагается, что оно прибудет очень быстро, но возможны и достаточно долгие задержки. Может случиться так, что сообщение не прибудет вообще, либо прибудет несколько раз. Когда вы отправляете запрос другому процессу и не получаете отклика, вы понятия не имеете, что произошло: потерялся ли запрос, либо тот другой процесс аварийно завершился, либо сам отклик потерялся? Или же на самом деле ничего не потерялось, сообщение просто задержалось и ещё может прибыть. Невозможно доподлинно узнать, что произошло, поскольку ненадёжный обмен сообщениями – единственный способ межпроцессной коммуникации.

Распределённые алгоритмы работают именно с такой моделью ненадёжной коммуникации и надстраивают над ней строгие гарантии. Примеры таких строгих гарантий – транзакции в базах данных и репликация (когда мы храним некоторые данные в виде нескольких копий на разных машинах, чтобы не потерять информацию, если одна из машин откажет).

К сожалению, распределённые алгоритмы печально известны тем, насколько сложно о них рассуждать, ведь заложенные в них гарантии должны соблюдаться независимо от того, в каком порядке доставляются сообщения (и соблюдаться даже в случае потери некоторых сообщений или отказа процессов). Многие алгоритмы устроены очень тонко, и одних лишь неформальных рассуждений недостаточно, чтобы гарантировать их корректность. Более того, количество возможных преобразований и перехлёстов конкурентных операций быстро становится слишком большим по меркам любого механизма проверки моделей, и исчерпывающим образом протестировать систему становится невозможно. Именно поэтому при работе с распределёнными алгоритмами так ценны варианты формального доказательства их корректности.

❯ Моделирование распределённой системы в Isabelle/HOL

В этой статье мы рассмотрим, как пользоваться доказательным инструментом Isabelle/HOL для формальной верификации некоторых распределённых алгоритмов. В Isabelle/HOL нет никакой встроенной поддержки распределённых вычислений, но, к счастью, смоделировать распределённую систему в этом инструменте не составляет труда. Это делается при помощи структур данных, предоставляемых в Isabelle/HOL – функций, списков и множеств.

Первым делом предположим, что у каждого процесса (или узла) в системе есть уникальный идентификатор, который может быть просто целым числом или строкой. В зависимости от алгоритма, набор ID процессов в системе может быть фиксированным и известным или неограниченным и неизвестным (второй вариант приемлем в системах, где новые процессы могут подключаться к работе, а по истечении некоторого времени выходить из системы).

Выполнение алгоритма – это последовательность дискретных шагов. В любой момент времени в одном из процессов происходит некоторое событие (одно из трёх): 1) получение сообщения, отправленного другим процессом, 2) получение пользовательского ввода, 3) истечение задержки.

datatype ('proc, 'msg, 'val) event
  = Receive (msg_sender: 'proc) (recv_msg: 'msg)
  | Request 'val
  | Timeout

Процесс, срабатывая в ответ на одно из этих событий, выполняет функцию, которая может обновить собственное состояние или отправлять сообщения другим процессам. Сообщение, отправленное на одном из таких шагов, может быть получено на любом из следующих шагов или не получено вообще.

У каждого процесса есть собственное локальное состояние, которого он не разделяет ни с одним другим процессом. В начале существования это состояние обладает фиксированным исходным значением, которое обновляется только по завершении процессом очередного шага. Процесс не может читать состояние другого процесса, но мы можем описать состояние всей системы как совокупность индивидуальных состояний всех процессов:

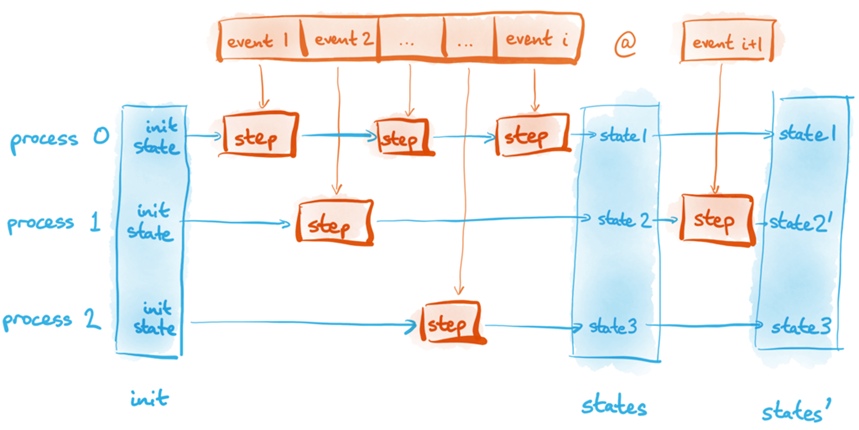
❯ Почему достаточно, чтобы шаги выполнялись в линейной последовательности

Хотя, в реальности процессы и могут выполняться параллельно, нам не требуется моделировать этот параллелизм, так как нас интересует только межпроцессная коммуникация (отправка и получение сообщений). Можно исходить из того, что процесс приступает к обработке любого события, только закончив обработку другого очередного события. Соответственно, любое параллельное выполнение эквивалентно некой линейной последовательности шагов. Другие формализации распределённых систем, в частности, язык TLA+, также работают с такой линейной последовательностью шагов.

Мы даже не пытаемся гадать, какой именно шаг выполняется каким процессом. Возможно, процессы «честно» запускаются по очереди, но не менее вероятно, что один процесс выполнит миллион шагов, а другой вообще ничего не сделает. Чтобы обойтись без таких версий об активности процессов, мы должны гарантировать корректную работу алгоритма независимо от распределения времени в системе. Например, временное отключение процесса от работы в сети можно смоделировать, просто создав процесс, который никогда не получает сообщений, даже в то время, пока другие процессы продолжают получать и отправлять сообщения.

В этой модели аварийное завершение процесса представлено просто как процесс, который по наступлении определённого момента времени больше ничего не делает; явно представлять аварийное завершение не требуется. Если мы хотим разрешить восстановление процессов после отказа, то можем добавить четвёртый тип событий, моделирующий рестарт процесса после отказа. При выполнении такого события «восстановление после отказа» процесс удалит все элементы собственного локального состояния, которые хранились в энергозависимой памяти, но сохранит те, что лежали в стабильном хранилище (на диске) и, соответственно, уцелели после отказа.

Рассуждая о безопасностных свойствах алгоритмов, лучше обойтись без любых допущений о том, какой процесс выполняется в какой момент времени, поскольку без такого показателя мы гарантируем, что алгоритм сможет справиться с произвольно долгими задержками при передаче сообщений. Если бы мы хотели судить о доступности алгоритма (например, быть уверенными, что рано или поздно он завершит работу), то должны были бы сделать определённые допущения о его честности – например, что любой неаварийный процесс рано или поздно совершит действие. Но в рассматриваемых здесь доказательствах мы до сих пор уделяли внимание лишь безопасностным свойствам алгоритма.



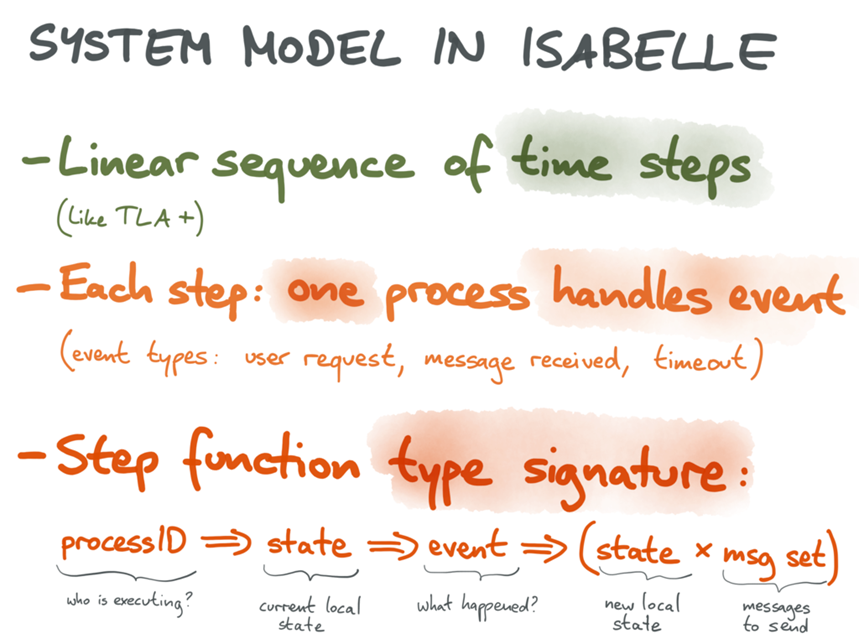
1// Линейная последовательность операций во времени (подобно TLA+);
2// На каждом шаге один процесс обрабатывает событие
(типы событий: пользовательский запрос, сообщение получено, задержка);
3// сигнатура типа ступенчатой функции:
ID процесса (кто исполнитель) => состояние (текущее локальное состояние) => событие (что произошло) = состояние (новое локальное состояние) + msg set (сообщение, которое должно быть отправлено).

Теперь можно выразить распределённый алгоритм как ступенчатую функцию, принимающую три аргумента: ID процесса, выполняющий операцию в данный момент; текущее локальное состояние данного процесса; произошедшее событие (получение сообщения, пользовательский ввод, задержка, восстановление после отказа). Возвращаемое значение состоит из нового состояния данного процесса и набора сообщений, которые должны быть переданы другим процессам (каждое сообщение помечается ID процесса-адресата).

type_synonym ('proc, 'state, 'msg, 'val) step_func =
  ‹'proc ⇒ 'state ⇒ ('proc, 'msg, 'val) event ⇒
  ('state × ('proc × 'msg) set)›

Актуальное состояние процесса в некоторый момент времени равно новому состоянию после предыдущего этапа для того же процесса (или исходному состоянию, если предыдущего шага не было). Предположив, что ступенчатая функция является детерминированной, мы можем закодировать любую операцию, выполняемую в системе, как список пар (идентификатор процесса, событие), указав таким образом серию произошедших событий, и в каком именно процессе они произошли. Конечное состояние системы получаем, вызывая ступенчатую функцию по одному разу на каждое событие.

❯ Определяем, что может произойти

Чтобы доказать корректность распределённого алгоритма, необходимо продемонстрировать, что он даёт правильный результат при любом варианте выполнения, то есть, применительно к любому возможному списку пар (идентификатор процесса, событие). Но какие варианты выполнения возможны? На самом деле, можно свободно допускать всего одну вещь: если сообщение получено процессом, то отправлено оно было именно этому процессу. Иными словами, мы рассчитываем, что сеть не фабрикует сообщения из ничего, и один процесс не может выдать себя за другой (в публичной сети, куда злоумышленник может внедрять поддельные пакеты, нам для установления подлинности пакетов потребуется их криптографически аутентифицировать, но эта тема выходит за рамки данной статьи).

Следовательно, сделаем единственное допущение: если в определённый момент было получено сообщение, то в некоторый предшествующий момент оно должно было быть отправлено. Но мы допускаем, что сообщения могут теряться, переупорядочиваться или неоднократно приходить к адресату. Давайте запрограммируем это допущение в Isabelle/HOL.

Сначала определим функцию, сообщающее, является ли возможным отдельно взятое событие: (valid_event evt proc msgs) возвращает true, если событие evt допускается в процессе proc в системе, где msgs – это множество всех сообщений, отправленных до сих пор. Msgs – это множество троек (отправитель, получатель, сообщение). Мы определяем, что событие Receive допускается тогда и только тогда, когда полученное сообщение присутствует в msgs, а события Request или Timeout допускаются в любой момент.

fun valid_event :: ‹('proc, 'msg, 'val) event ⇒ 'proc ⇒
                	('proc × 'proc × 'msg) set ⇒ bool›
where
  ‹valid_event (Receive sender msg) recpt msgs =
	((sender, recpt, msg) ∈ msgs)› |
  ‹valid_event (Request _) _ _ = True› |
  ‹valid_event Timeout _ _ = True›

Далее определяем множество всех возможных последовательностей событий. Для этого используем в Isabelle индуктивный предикат: (execute step init procs events msgs states) возвращает true, если events – это действительная последовательность событий при выполнении алгоритма, где step – это ступенчатая функция, init – это исходное состояние каждого процесса, а proc – множество всех процессов в системе (которое может быть бесконечным, если мы допускаем любое количество процессов). Два последних аргумента отслеживают состояние выполнения: msgs – это множество всех сообщений, отправленных до сих пор, а states – отображение идентификатора процесса на состояние данного процесса.

inductive execute ::
  ‹('proc, 'state, 'msg, 'val) step_func ⇒ ('proc ⇒ 'state) ⇒
   'proc set ⇒ ('proc × ('proc, 'msg, 'val) event) list ⇒
   ('proc × 'proc × 'msg) set ⇒ ('proc ⇒ 'state) ⇒ bool›
where
  ‹execute step init procs [] {} init› |
  ‹⟦execute step init procs events msgs states;
	proc ∈ procs;
	valid_event event proc msgs;
	step proc (states proc) event = (new_state, sent);
	events' = events @ [(proc, event)];
	msgs' = msgs ∪ {m. ∃(recpt, msg) ∈ sent.
                   	m = (proc, recpt, msg)};
	states' = states (proc := new_state)
   ⟧ ⟹ execute step init procs events' msgs' states'›

Согласно этому определению, пустой список событий действителен в случае, когда система находится в исходном состоянии, и никаких сообщений не отправлено. Более того, если последовательность событий events до сих пор является действительной, а event разрешено быть в данном состоянии, то можно вызвать ступенчатую функцию, добавить в msgs любые отправляемые ею сообщения, обновить состояние соответствующего процесса – и получить в результате другую действительную последовательность событий.

Вот и всё, что нам требуется, чтобы смоделировать распределённую систему!

❯ Доказательство корректности алгоритма

Теперь можно взять некоторый алгоритм (определяемый ступенчатой функцией и исходным состоянием) и доказать, что для всех возможных списков событий соблюдается некоторое свойство P. Поскольку максимальное количество совершаемых шагов не фиксируется, у нас бесконечно много возможных списков событий. Но это не проблема, поскольку доказать P можно путём индуктивной обработки списков.



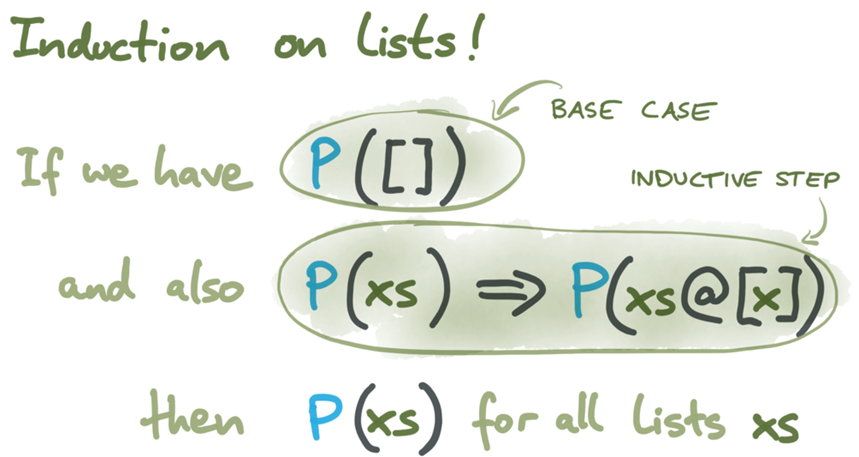
Induction on lists // списковая индукция
Base case // базовый случай
Inductive step // шаг индукции
If we have // если
And also // и при этом
Then // то

Воспользуемся правилом индукции List.rev_induct в Isabelle/HOL. Оно требует продемонстрировать, что:

1. свойство P истинно для пустого списка (т.e., для системы в исходном состоянии, в котором ещё никакие шаги не выполнялись); и
2. если свойство P истинно при некотором варианте выполнения, и мы удлиним этот процесс выполнения ещё на шаг, то и после этого шага P по-прежнему будет соблюдаться.

Иными словами, мы доказываем инвариантность P для всех возможных состояний в масштабах всей системы. В Isabelle данное доказательство имеет примерно следующий вид (где step, init и procs правильно определены):

theorem prove_invariant:
  assumes ‹execute step init procs events msgs states›
  shows ‹some_invariant states›
using assms proof (induction events arbitrary: msgs states
               	rule: List.rev_induct)
  case Nil
  then show ‹some_invariant states› sorry
next
  case (snoc event events)
  then show ?case sorry
qed

Самое сложное при верификации распределённых алгоритмов – отыскать подходящий инвариант, который одновременно верен и подразумевает те свойства, которые вы желаете предусмотреть в вашем алгоритме. К сожалению, проектировать такой инвариант приходится вручную. Но, как только у вас будет в распоряжении кандидатура такого инварианта, при помощи Isabelle очень удобно проверить, корректен ли он и достаточно ли крепок, чтобы соответствовать всем вашим целям.

Подробнее о том, как доказать корректность простого алгоритма консенсуса в рамках такой модели рассказано в двухчасовой лекции, где с азов рассмотрен демонстрационный пример (опыта работы с Isabelle не требуется). Также доступен демонстрационный код Isabelle.