Спустя 10 лет опыта работы по специальности после завершения института настал тот самый первый случай, когда понадобилось вспомнить преобразование Фурье из курса спец разделов математического анализа.
Допустим у нас есть сигнал с очень зашумленной высокочастотной составляющей. Для конкретики пусть это будет график естественной освещенности от времени. Вот например такой:
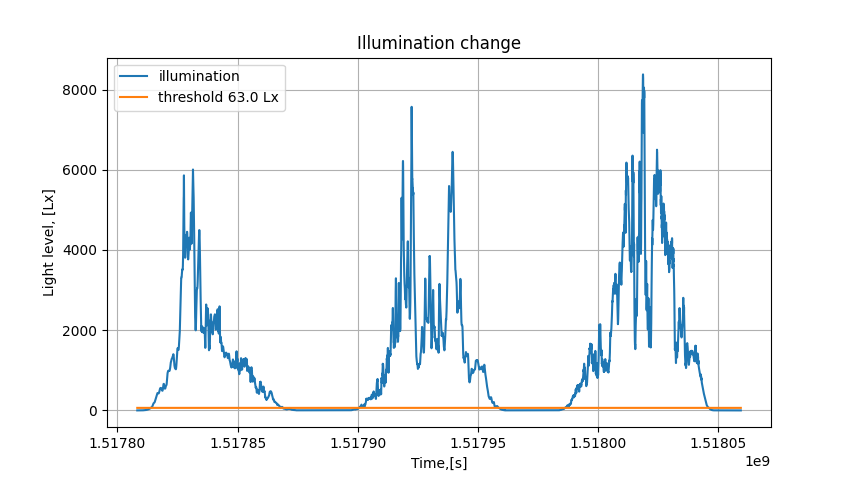
При этом интерес представляет самая низкочастотная составляющая этого сигнала. Та, которая с периодом около 24х часов. Надо определить амплитуду, фазу и желательно точную частоту самой первой гармоники.
Вот этот сигнал измерен реальным физическим датчиком освещенности BH1750 и записан в текстовый *.csv файл.
...
1989, 1410.000, 17.75, 10:12:39, 13/7/2023, 1517845015
1990, 1413.333, 17.75, 10:12:59, 13/7/2023, 1517845035
1991, 1415.833, 17.75, 10:13:19, 13/7/2023, 1517845055
1992, 1420.833, 17.75, 10:13:39, 13/7/2023, 1517845075
1993, 1424.167, 17.75, 10:13:59, 13/7/2023, 1517845095
...Ось X-это 6й столбец, Ось Y-2ой столбец. При этом стоит задача выделить фазу этого сигнала. Проще говоря, надо найти момент времени, когда происходит максимум усреднённого сигнала.
Как же выделить фазу зашумленного сигнала?
Понятно, что надо сперва как-то обобщить этот зашумленный сигнал. Пропустить его через фильтр нижних частот.
Если мы пропустим сигнал через цифровой фильтр скользящего среднего (FIR фильтр), то выходной сигнал сместится по фазе вправо и реальная фаза окажется искажена. Нужен другой способ.
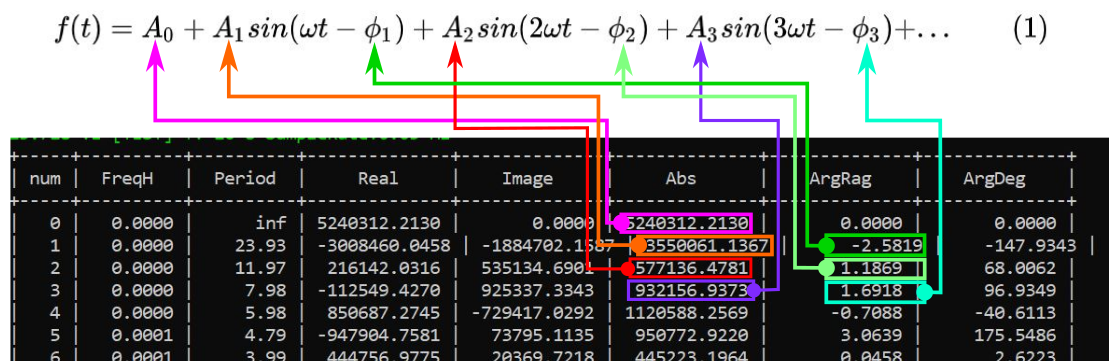
Из курса высшей математики известно, что любую периодическую и кусочно-непрерывную функцию можно представить в виде суммы синусов разной амплитуды и разных фаз согласно формуле (1)
Это ряд Фурье. Если повышать количество слагаемых (гармоник), то можно уменьшить среднеквадратическую ошибку между исходным сигналом и функцией составленной при помощи этих синусов.

Если оставить только первые низкочастотные гармоники, то получится, что как-будто сигнал пропустили через абстрактный фильтр нижних частот.

Как же вычислить коэффициенты ряде Фурье?
Надо воспользоваться дискретным преобразованием Фурье (DFT). Это чисто численная процедура. Даешь массив исходного сигнала произвольного размера N, указываешь частоту дискретизации (для данного эксперимента это 20 секунд), делаешь вычисления и получаешь массив комплексных чисел той же размерности N.
bool dft_calc(const double* const signal, uint32_t n_big, double complex* const dft_out, uint32_t out_len,
double t_big) {
LOG_INFO(DFT, "Calc %u Samples", n_big);
bool res = false;
double measure_interval_s = ((double)n_big) * t_big;
if(signal) {
res = true;
uint32_t k = 0;
for(k = 0; k < n_big; k++) {
dft_out[k] = 0.0 + 0.0 * I;
uint32_t n = 0;
for(n = 0; n < n_big; n++) {
dft_out[k] += ((double)signal[n]) * (cos(TWO_PI_VAL * ((double)k * n) / ((double)n_big)) -
sin(TWO_PI_VAL * ((double)k * n) / ((double)n_big)) * I);
}
dft_out[k] = 2.0 * dft_out[k] / ((double)n_big);
}
}
return res;
}В данной реализации временная сложность DFT составляет O(N^2) где N количество элементов в выборке сигнала.
Вот спектр данного сигнала. Тут период в часах.
Модуль комплексного числа будет амплитудой синуса, аргумент комплексного числа будет фазой синуса. Дале просто подставляем эти числа в формулу (1) и получается результат фильтрации.
Вот несколько разложений в ряд Фурье до первой гармоники. Как видно на глаз фаза определилась достаточно достоверно.
К слову преобразование Фурье это настоящий трудяга в IT. Он отлично подходит для сжатия периодических данных. Вместо огромного файла лога периодического сигнала Вы просто сохраняете массив из нескольких пар вещественных коэффициентов для амплитуды и фазы данной конкретной гармоники ряда Фурье. Далее по этим коэффициентам функция примерно восстанавливается до той степени точности которая вам нужна. Однако происходит потеря качества исходного сигнала. То есть ряд Фурье можно использовать для компрессии экспериментальных данных.
Также преобразование Фурье используется для демодуляции радио сигналов в которых происходит фазовая, частотная и амплитудная модуляции.
Достоинства фильтра низких частот на преобразовании Фурье:
1. Если вычислить DFT, обнулить высокие частоты и вычислить обратное DFT, то не меняется фаза тех низкочастотных гармоник, которые мы оставили.
Фильтр на основе преобразования Фурье отлично подходит для пост обработки на PC.
Недостатки фильтра низких частот на преобразовании Фурье:
Сложно себе представить работу такого фильтра в реальном масштабе времени. Ведь надо много вычислений O(n^2). В идеале хочется вычислять преобразование Фурье для последних N тактов, отбрасывать высокочастотные гармоники и вычислять обратное преобразование Фурье. Это еще O(n) действий. И всё это должно происходить за один такт. Но это запредельно много вычислений по сравнению с тем же FIR фильтром.
Надо заранее знать самую низкую частоту сигнала. Получившаяся формула ряда Фурье будет отрисовывать график сигнала с периодом равным размеру выборки умноженную на период дискретизации. Таким образом преобразование Фурье заводится только "с толкача". Преобразованию Фурье надо на самом первом шаге давать подсказку (период первой гармоники).
Преобразование Фурье не очень подходит для непериодических сигналов. Для непериодических сигналов надо смотреть в сторону Вейвлет преобразований.
Преобразование Фурье показывает вклад частот f=1/T, 2f, 3f. Но преобразование Фурье не покажет вклад частоты 0.5f, 1.5f, 2.5f. Вернее покажет, если вы в два раза увеличите выборку 2T и выполните новое отдельное преобразование обработав при этом в 2 раза больше данных.
Вывод
Из преобразования Фурье можно сделать фильтр нижних частот. Преобразование Фурье отлично находит не только частоты внутри сигнала, но также находит и фазы этих частот.
Теория рядов Фурье отлично подходит для пост обработки периодического сигнала, если нужно выделить какие-то отдельные частоты в этом сигнале.
Вообще фильтровать сигналы преобразованием Фурье это нетипичный use-сase. Обычно настраивают цифровые фильтры для фильтрации. Но это только подтверждает цитату Барнса Уоллеса (Barnes Wallis)
Чем меньше Вы знаете о предмете, тем выше Ваша способность для представления оригинальных идей
В общем, вступайте в ряды Фурье! Сходимость! Равенство! Гильбертово пространство!
Словарь
Акроним |
Расшифровка |
FIR |
finite impulse response |
DFT |
Discrete Fourier Transform |
PC |
Personal computer |
FFT |
Fast Fourier transform |
FIR |
Finite Impulse Response |
Links
http://www.mathprofi.ru/ryady_furie_primery_reshenij.html
https://www.youtube.com/watch?v=i7dPkwKHFr0
http://latex.codecogs.com/eqneditor/editor.php
https://code911.top/howto/how-to-run-python-script-from-https://pyneng.readthedocs.io/ru/latest/book/05_basic_scripts/args.html
https://ezgif.com/maker
https://habr.com/ru/articles/269991/
https://habr.com/ru/articles/196374/
https://habr.com/ru/articles/324152/
Комментарии (52)

berng
23.07.2023 01:43+4FIR фильтры, DFT в цифровой обработке сигналов? Назад в прошлое?
Используйте БИХ-фильтры и fft, их уже минимум 80 лет как раз для этого изобрели (или 220 лет назад, смотря как считать), и работают они намного быстрее.
По крайней мере БИХ-фильтром можно реализовать примитивную низкочастотную фильтрацию за три арифметических действия очень легко:
OUT(t)=(1-a)*OUT(t-1)+a*IN(t)
a \in [0,1]
Чем меньше a, тем у'же полоса НЧ фильтрации. Если нужен более резкий срез в частотной области, добавляют элементов в правой части из OUT и IN, для деталей почитайте про проектирование БИХ-фильтров, есть и готовые программки для расчета коэффициентов для заданных характеристик фильтров.
Ведь 10 операций сложение/умножение для непосредственного получения фильтрованного сигнала при БИХ-фильтрации выполняются значительно быстрее, чем 10^5 .. 10^6 операций при DFT или 10^3..10^4 при FIR.

SpiderEkb
23.07.2023 01:43+2Вообще в описанной задаче больше подошло бы двойное или тройное экспоненциальное сглаживание.
Кстати, то, что написали Вы, иначе называется просто экспоненциальным сглаживанием.
Все три варианта отлично подходят для потоковой обработки данных.
Есть и более сложные (вычислительно) фильтры. Например, Ходрика-Прескотта
Вообще, тема анализа временных рядов (в т.ч. и с учетом сезонности) исследована достаточно глубоко.

berng
23.07.2023 01:43+1Насчет экспоненциального сглаживания согласен. А если попробовать вместо a=-0.5, а вместо (1-a)=0.5 то получите фильтр высоких частот. В общем, БИХ - очень широкий и эффективный класс фильтров, где можно сравнительно небольшим числом операций решать достаточно сложные задачи.

0tt0max
23.07.2023 01:43+1БИХ фильтр искажает ФЧХ, что в ряде задач недопустимо. Выходом может быть блочная обработка и filtfilt, но при этом невозможно обрабатывать сигнал в реальном времени.

berng
23.07.2023 01:43+1Никогда особно не вникал в эту проблему (чаще всего работал с реальными данными, а у них фаза всегда 0, поэтому 'фазовых искажений' нет в принципе), но по построению для комплексной области это зависит от фазы коэффициентов. Если исходный сигнал задан с фазой (в комплексном виде или в квадратурных компонентах ), то скорее всего можно сделать фазовый доворот комплекснозначных коэффициентов a_i, b_i для необходимой компенсации фазы или ФЧХ. При необходимости это можно делать в динамике, 10 комплексных умножений много времени не сожрут.

HiTechSpoon
23.07.2023 01:43+1Фаза у любых реальных сигналов, у которых может гулять частота, будет смещаться в зависимости от ФЧХ БИХ фильтра. Тут компенсировать фазу может оказаться сложновато. Обычно БИХ применяются там, где важна амплитуда, а не фаза; либо там, где частота сигнала находится вдали от сильных искажений.
Не всегда БИХ/КИХ фильтры подходят под задачу. БПФ, например, неплохо подходит там, где нужно отфильтровать сигнал и получить фазу сигнала одновременно. Приходится подбирать инструменты под задачу и все таки это не "назад в прошлое".

berng
23.07.2023 01:43В принципе, да, в каком-то смысле согласен. Но есть одно но - терминологическая путаница. Фазы у реальнозначных сигналов нет, потому она и смещаться никуда не может. Эта терминологическая ошибка - исключительно проблема их неудачного представления в виде ряда Фурье.
Для реальных сигналов представление в виде ряда Фурье используется традиционно, но оно не совсем корректно. Отсюда и возникающие проблемы с кажущейся фазой (которой реально нет, ведь для реальнозначных сигналов есть лишь задержки). Если использовать более корректное для этого случая преобразование Хартли (где в качестве базовой функции выступает cas(x)=cos(x)+sin(x), которое еще и считается в 2 раза быстрее, чем БПФ), проблем с фазой (которой нет) не возникнет, как того и ожидается для реальнозначных сигналов, у которых фаза нулевая всегда по определению. Просто преобразование Хартли корректный, но не очень общепринятый метод анализа.
Ну а в электрических схемах нужно использовать квадратурные компоненты сигнала (или пару ток-напряжение), для них все честно и корректно, и фазовая информация не теряется.
Но в принципе вы правы - для использования фильтров надо очень аккуратно подбирать их параметры, в отличие от преобразования Фурье, где можно легко реализовать любой фильтр просто умножением и не думать о реализуемости такого фильтра в виде импульсного отклика.

Uint32
23.07.2023 01:43+2Фаза у любых реальных сигналов, у которых может гулять частота, будет смещаться в зависимости от ФЧХ БИХ фильтра. Тут компенсировать фазу может оказаться сложновато.
Есть достаточно простой приём для коррекции ФЧХ любых IIR и FIR - после фильтрации сделать ещё одну обратив во времени полученный сигнал. ФЧХ скомпенсируется, а частотные свойства фильтра улучшатся.

N-Cube
23.07.2023 01:43+6Сезонные данные так не анализируют- потому что, к примеру, солнце всходит и заходит в разное время каждый день. Отфильтровать можно с помощью оконного фильтра Гаусса (как любой оконный фильтр, легко применим и к потоковым данным с некоторым аккумулятором). А для полноценного разложения на константу, тренд и сезонную компоненту (или компоненты) есть специальные методы, см. https://www.statsmodels.org/dev/examples/notebooks/generated/stl_decomposition.html
P.S. Давно уже придумано оконное преобразование Фурье, или вейвлеты, которые намного лучше применимы в мире не-бесконечных сигналов.

Oksenija
23.07.2023 01:43+2В софте типа гитарных процесоров фильтр - Ких - импульсная реакция колонки или "гитарноного кабинета" как вычисляется ких фильтром на скользящем БПФ в РЕАЛЬНОМ врмени, причем импульсная реакция колонки или длина КИХ может быть скажем 65к точек и все работает в реальном времени на умеренно мощных процессорах. И это уже примерно как 7..10 лет существует. Подробнее вот ссылка https://guitarclan.com/free-cabinet-impulse-responses/ Добавлю именно в реальном времени и именно на бесконечном потоке данных и о ужас даже с задержкой близкой к нескольким миллисекундам, теория математики этого отлично разработана и опубликована в открытых источниках, довольно сложна, но это так на самом деле КИХ на БПФ организованный определеным хитрым способом почти не имеет задержки из-за какзалось обязательного буферизирования данных для блока БПФ - а вот и нет, математики это решили! (хитрое каскадиование и переменных длины буфер от 1 мс до нескольких секунд). Гитаристы играют в живую через плгуины VST с фильтрами КИХ на БПФ с длиной импульса скажем в 0.5 сек или 22000 отсчетов с задержкой 5..10 мс! (или 256 отсчетов) Да задержка меньше длины КИХ фильтра в примерно 100 раз. Казалось бы невозможно - но это факт и алгоритмы для этого легко гугляться. (фильтр на скользащем БПФ)

N-Cube
23.07.2023 01:43+2Добавлю именно в реальном времени и именно на бесконечном потоке данных и о ужас даже с задержкой близкой к нескольким миллисекундам, теория математики этого отлично разработана и опубликована в открытых источниках, довольно сложна, но это так на самом деле КИХ на БПФ организованный определеным хитрым способом почти не имеет задержки из-за какзалось обязательного буферизирования данных для блока БПФ - а вот и нет, математики это решили! (хитрое каскадиование и переменных длины буфер от 1 мс до нескольких секунд).
Бесконечного потока данных не бывает, в лучшем случае, есть непрерывный. А вот на границах разрывов сигнала что происходит? (ничего хорошего). Далее, сначала вы клянетесь про «задержкой близкой к нескольким миллисекундам», а потом «буфер от 1 мс до нескольких секунд» - тут разница на три порядка. После начала регистрации сигнала или его резком изменении сколько времени заполнения буфера ждать? Более того, и в микросекундном интервале бывает достаточно отсчетов для обработки сигналов, и наоборот (вы годовые изменения с миллисекундным буфером изучать собрались?), так что считать в единицах времени, а не в количестве отсчетов - вообще бессмысленно. Не надо ссылаться на «теорию математики», надо с фактами поаккуратнее обращаться.

diakin
23.07.2023 01:43+1длиной импульса скажем в 0.5 сек или 22000 отсчетов с задержкой 5..10 мс!
Задержка имеет место быть в начале, сначала должны пройти эти 22000 отсчетов для вычисления отклика, а потом отфильтрованный сигнал будет обновляться с приходом каждого нового отсчета. Ну или как там будет успевать обсчитывать процессор.
Для простого скользящего среднего сначала приходят эти 22000 отсчетов, вычисляется среднее, а потом с приходом нового отсчета к полученному прибавляется этот отсчет
Xn+1 /22000 и вычитается первый отсчет X0/22000 .

AAngstrom
23.07.2023 01:43+6--Сложно себе представить работу такого фильтра в реальном масштабе времени. Ведь надо много вычислений O(n^2)
Вам ещё предстоит открыть для себя быстрое преобразование Фурье (FFT: fast Fourier transform).
--Преобразование Фурье не подходит для непериодических сигналов.
Вы, похоже, путаете ряд Фурье и преобразование Фурье. Или нет. В любом случае, это утверждение не верно. Совсем. Преобразование Фурье от гауссовой функции смотрит на Вас с осуждением.
--Если вычислить DFT, обнулить высокие частоты и вычислить обратное DFT,
то не меняется фаза тех низкочастотных гармоник, которые мы оставили.Когда частотное представление получено, его можно умножить на любую функцию частоты, не обязательно ступеньку. В частности, подобрав должным образом коэффициенты, можно получить тот самый FIR.
А вообще, сигналы можно фильтровать с помощью (почти) любого разложения по полной ортогональной системе функций ([напр.](https://core.ac.uk/download/36719692.pdf)). И даже необязательно ортогоноальной (см. вейвлеты).

aabzel Автор
23.07.2023 01:43Вам ещё предстоит открыть для себя быстрое преобразование Фурье (FFT: fast Fourier transform).
FFT работает только с сигналами размер выборки которых равен степеням двойки. А тут размер выборки непредсказуемый. Поэтому FFT не подходит.

Refridgerator
23.07.2023 01:43Вам ещё предстоит открыть для себя быстрое преобразование Фурье произвольного размера, а не только степеней двойки.

pvvv
23.07.2023 01:43+8Если вычислить DFT, обнулить высокие частоты и вычислить обратное DFT, то не меняется фаза тех низкочастотных гармоник, которые мы оставили.
Умножение в частотной области (на ступеньку с занулением определённых частот) == свёртка во временной, ровно то что КИХ фильтры и делают без преобразования туда обратно.
Фаза и так не портится, ФЧХ абсолютна линейна и соответствует просто задержке на половину длины фильра.
Ваше "скользящее среднее" просто надо считать не от X[i]..X[i+N] а от X[i-N/2] до X[i+N/2], и внезапно ничего никуда смещаться не будет.

Krasnoarmeec
23.07.2023 01:43+2Раз уж заговорили про фильтры, не могу не порекомендовать статью "On fast FIR filters implemented as tail-canceling IIR filters" про TIIR-фильтры. С кодом на C (осторожно, там вроде была ошибка!).

Serge78rus
23.07.2023 01:43+2При этом интерес представляет самая низкая частотная составляющая этого
сигнала. Та которая с периодом 24 часа. Надо определить амплитуду и фазу
самой первой гармоники.Понятно, что надо как-то обобщить этот сигнал. Пропустить его через фильтр нижних частот.
Если мы пропустим сигнал через цифровой фильтр скользящего среднего (FIR
фильтр), то выходной сигнал сместится по фазе вправо и реальная фаза
окажется искажена. Нужен другой способ.Почему для выделения первой гармоники Вы используете ФНЧ, а не узкополосный полосовой фильтр? Простейший аналог из схемотехники - фильтр на основе одиночного колебательного контура. На частоте резонанса он не дает фазового сдвига.

aabzel Автор
23.07.2023 01:43Почему для выделения первой гармоники Вы используете ФНЧ, а не узкополосный полосовой фильтр?
Потому что частота первой гармоники в реальности не известна.

pvvv
23.07.2023 01:43+1а для этого есть автокорреляция,
и затем гражданин Герцель для DFT с одним умножением на отсчёт, без тригонометрии.

Serge78rus
23.07.2023 01:43+1А какую тогда Вы хотели установить частоту среза ФНЧ?

aabzel Автор
23.07.2023 01:43А какую тогда Вы хотели установить частоту среза ФНЧ?
Очень низкую.
Fc = 1.0/(30.0*3600.0 [s] )= 9.259259259259259e-06 [Hz]
Serge78rus
23.07.2023 01:43+1Исходя из чего принято такое значение? Ведь тогда первая гармоника из Вашего же примера попадает за границу полосы пропускания. Это далеко от принципов оптимальной фильтрации сигналов, используемых для максимизации соотношения сигнал/шум. Ну а про фазовые сдвиги сигнала за пределами полосы пропускания и говорить нечего - чем круче фильтр, тем хуже будет ситуация с фазой. А насколько можно понять из Вашей же постановки задачи - фаза для Вас важна.

aabzel Автор
23.07.2023 01:43Исходя из чего принято такое значение?
Я хочу экспериментально увидеть в преобразовании Фурье, что период первой гармоники графика естественной освещенности на самом деле не точно равен 24 часа, а немного меняется в течении года, так как Земля движется вокруг Солнца по эллипсу и угол доворота на Солнце каждый день разный.

Serge78rus
23.07.2023 01:43+1То есть Вам нужна только временная характеристика сигнала - частота или фаза? А в статье Вы писали:
Надо определить амплитуду и фазу самой первой гармоники.
Я думаю, что такой "разброд" мнений комментаторов вызван именно нечеткой формулировкой постановки задачи.

diakin
23.07.2023 01:43-1Лучше это сначала смоделировать, как там меняются углы освещенности при движении по эллипсу, сгенерировать отсчеты и подсунуть эту выборку Фурье.
Если результат совпадет с ожидаемым, то хорошо.

Radisto
23.07.2023 01:43+1задача сводится к изменению первой гармоники с точностью в районе сотых долей процента. При этом вариация частоты полностью компенсируется всего на 365 циклах. Выглядит сложно. Мне почему-то кажется, что придется отслеживать период одного колебания точнее. Например щелевой колпачок на фотодатчик. Тогда разность фаз между сигналом и им же, сдвинутым на сколько-то дней, будет явно видна.
Безумная идея, не судите строго:
Фотодатчик, естественно неподвижный относительно земли. На него надеваем щелевой колпачок. нацелим его скажем на юг, чтобы в моменты срабатывания сигнал был повеселее. внутри вся камера с фотодатчиком должна быть зачернена. Замер проводим строго в одно и то же время суток по таймеру. Если щель достаточно узка, а датчик от неё далёк, то он по идее должен выдавать пики на частоте средних солнечных суток (по таймеру же), амплитудно промодулированных солнцем (оно будет то входить в щель, то недоходить/переходить. Частота модуляции наверное будет искомыми отклонениями. очевидный минус - погодой эта частота тоже будет промодулирована.

Radisto
23.07.2023 01:43+1А если попробовать вычесть друг из друга сигналы? За второй сигнал взять первый, но сдвинутый на полгода/год. Будет похоже на биения? И взять Фурье уже от этих биений - может выйдет точнее. Очередная безумная мысль, прошу прощения

oshpeg
23.07.2023 01:43+2А еще, обнуление бинов тождественно накладыванию прямоугольного окна, что во временной области даст бесконечный КИХ.

diakin
23.07.2023 01:43+2Если мы пропустим сигнал через цифровой фильтр скользящего среднего (FIR фильтр), то выходной сигнал сместится по фазе вправо и реальная фаза окажется искажена.
Это если вы пытаетесь получать результат в реальном времени. Потому что если пытаться усреднять сигнал на каком-то отрезке времени, то первые значения усредненного сигнала будут готовы после окончания этого отрезка. Если вы проводите постобработку, то всегда можно отнести значения отфильтрованного сигнала к "правильным" моментам времени.
То есть сместить их назад на половину периода усреднения.

diakin
23.07.2023 01:43+2Надо определить амплитуду и фазу самой первой гармоники.
И что означает "фаза" в данном контексте? Вот у вас есть синусоидальный сигнал, вы в произвольный момент времени начали измерения.. Так фаза в этом случае будет зависеть от того в какую точку синусоиды попало начало измерения. То есть понятие фазы в данном случае бессмысленно. Фаза имеет смысл когда есть два сигнала одинаковой (ну или близкой) частоты - опорный, по которому стартуют измерения и исследуемый сигнал, фаза которого вычисляется относительно опорного.
Ну или вы стартуете измерения в 0:00 часов по местному времени и измеряете освещенность от восхода солнца. Тогда фаза сигнала освещенности будет отсчитываться относительно этих 0:00 часов.
Тут и изображать ФНЧ не требуется. Вы производите измерения в течение 24 часов, получаете выборку, затем через Фурье вычисляете амплитуду и фазу первой гармоники.
aabzel Автор
23.07.2023 01:43И что означает "фаза" в данном контексте?
Проще говоря, найти момент времени, когда происходит максимум усреднённого сигнала.

aabzel Автор
23.07.2023 01:43Ну или вы стартуете измерения в 0:00 часов по местному времени и измеряете освещенность от восхода солнца. Тогда фаза сигнала освещенности будет отсчитываться относительно этих 0:00 часов.
Нет. Я измеряю освещенность не по местному времени, а по UTC+0. Поэтому фаза как раз меняется при перемещении по параллелям.

diakin
23.07.2023 01:43+1Ну это без разницы, всегда можно внести поправку на часовой пояс.
Сутки длятся 24 часа, за это время происходят все события - восход Солнца, макс. высота, заход Солнца. Потом все повторяется. То есть период равен 24 часа.
Но время захода и восхода немного сдвигается каждый день. Максимальная высота Солнца всегда в полдень.
Тогда измерения ведутся 24 часа (длительность выборки 24 часа). Начало отсчета выбирается произвольно, какое требуется. Потом делается Фурье (FFT например, да любое), вычисляется амплитуда и фаза первой гармоники. Потом измерения повторяются, фаза при этом будет наверное ползти, потому что время восхода\захода поменяется.
Освещенность прямо пропорциональна высоте Солнца над горизонтом? Так это табличные значения вроде?
Можно для тестирования модели погонять эти табличные значения, подсунуть их в Фурье анализ.
aabzel Автор
23.07.2023 01:43Но время захода и восхода немного сдвигается каждый день.
Для неподвижного наблюдателя эти времена сдвигаются в разные стороны. Либо от либо к друг другу.

aabzel Автор
23.07.2023 01:43Потом измерения повторяются, фаза при этом будет наверное ползти, потому что время восхода\захода поменяется.
Вот именно что фаза для неподвижного наблюдателя никуда ползти не должна.

aabzel Автор
23.07.2023 01:43Освещенность прямо пропорциональна высоте Солнца над горизонтом? Так это табличные значения вроде?
Это вообще по астрономическим формулам чисто аналитически вычисляется.

Radisto
23.07.2023 01:43+1сутки длятся не 24 часа. в этом и суть

diakin
23.07.2023 01:43+1А сколько длятся сутки?
... Вследствие того, что орбита, по которой Земля движется вокруг Солнца, не является окружностью, а ось суточного вращения Земли имеет наклон к плоскости орбиты (из-за чего на Земле происходит смена времён года), истинное солнечное время неравномерно. Максимальная разница в продолжительности истинных солнечных суток в течение года составляет примерно 50 с.
Ну то есть получается что есть средняя за год длительность суток и мгновенная истинная длительность между двумя кульминациями. Причем мгновенная длительность гуляет относительно средней в течение года.
Но освещенность может зависеть от облачности. Первые полдня будут тучи, а вторые солнечно. И максимум освещенности сместится на вторую половину, независимо от положения солнца.
Radisto
23.07.2023 01:43+1Верно. Но с другой стороны, облачность может быть и одинаковой в обеих половинах суток и ничего не сместить.

Refridgerator
23.07.2023 01:43+1Абсолютно все утверждения из статьи ошибочны и не соответствуют действительности. Автор не виноват, в информационном пространстве вокруг преобразования Фурье магии и городских легенд намного больше, чем вменяемой информации, в том числе и в ВУЗ-ах, преподаватели в которых ни разу не использовали теорию на практике. И теория эта совсем не простая для настоящего понимания её сути, а не просто фантазий на тему.
В частности, преобразования Фурье есть 4 вида:
а) непрерывный сигнал, непрерывный спектр;
б) непрерывный сигнал, дискретный спектр;
в) дискретный сигнал, непрерывный спектр;
г) дискретный сигнал, дискретный спектр;Теория обычно даётся для а), но численно доступно только г). Отсутствие понимания того, как все эти типы соотносятся, и приводят к большинству заблуждений.
Далее нужно разобраться, что такое свёртка, как она соотносится с корреляцией, с которой многие уже знакомы через мат.статистику, в чём отличие линейной свёртки от циклической, и в чём смысл мантры "свёртка во временной области равно умножению в частотной и наоборот". Да, низкочастотная фильтрация осуществляется умножением высоких частот на ноль или около того.
С комплексными числами надо разобраться и главное с тем, откуда их взял сам Фурье. Затем — с преобразованием Хартли, которое обходится без комплексных чисел, и как оно соотносится с Фурье.
Ну и напоследок — скользящее среднее это не FIR, а его частный случай. И его, между прочим, можно вычислить за O(1).

aabzel Автор
23.07.2023 01:43+1Абсолютно все утверждения из статьи ошибочны и не соответствуют действительности.
Тем не менее я смог вычислить то, что хотел: нашел фазу усредненного сигнала от освещенности. Значит достаточно понимания, чтобы решать реальные задачи.

Refridgerator
23.07.2023 01:43-2Выше уже намекали на то, что подобная формулировка некорректна. Если вы решили какую-то свою задачу - это замечательно, но не отменяет полной оторванности содержания вашей статьи от реальности.

Refridgerator
23.07.2023 01:43Вот простой пример, как максимум первой гармоники может отличаться от максимума их суммы:

А ведь здесь их только три и даже нет сдвигов по фазе. Поэтому, если ваша задача состояла в поиске фильтрованного максимума — то найденное вами решение, скажем так, слегка неточное.
aabzel Автор
23.07.2023 01:43В эксперименте, что в тексте выделяется фаза только первой гармоники. Она представляет ключевой интерес.
Остальные гармоники не имеют существенного значения. Всё что после k=1 это просто мусор.

sci_nov
23.07.2023 01:43+1Если у вас отсчёты сигнала идут равномерно и известен период, то проблем-то особых нет. Берёте ДПФ от отрезка сигнала за один период, затем усредняете квадраты амплитуд гармоник по многим следующим отрезкам. Далее измеряете амплитуду первой гармоники. Параллельно усредняете фазу. Чем больше отрезков, тем точнее результат.



Sap_ru
Кодек MP2/3 смотрит с недоумением и с перепуга пытается начать крутить песни по кругу в попытке сделать их периодическими...
На этом месте MP3 заплакал и ушёл, прихватив с собой половину современной электроники, а среди математиков и программистов началась повальное пьянство.
Интересно у с тут получается. Что значит "самую низкую"? Если у вас периодический сигнал, то волшебным образом "самая низкая частота" равна его периоду. А если непериодический, то разложение Фурье совершенно точно по вашим же словам к нему не применимо, и в рамках предлагаемой логики вопрос не имеет смысла. Да и вообще, нижняя граница частоты непериодического сигнала равна его длительности, что судя по всему делает спектральную обработку таких сигналов если не невозможной, то невероятно сложной.
Radisto
Самая низкая - это разве не нулевая (постоянная составляющая)?
aabzel Автор
Ситуация такая:
Есть таблица чисел от измерения сигнала. Про этот сигнал мало что известно (ровным счетом ничего).
Не известна даже частота его самой низкочастотной гармоники. Не ясно сколько отсчетов брать для преобразования DFT.
Как определить период самой длинной гармоники, если, например, записана выборка всего длительностью t=0.75*T от этого самого длинного периода T?
Тут преобразование Фурье не поможет.
Sap_ru
Тут перепутана лошадь и повозка, сдаётся мне. Нужно как раз наоборот - получить спектр и выбрать необходимую частоту, ниже которой сделать сигнала уже не интересна для ожидаемого результата обработки. Очевидно, что даже не нужно строить полный спектр, достаточно построить только интересующий низ и с интересной дискретностью. Короче, такой проблемы нет, а если она по какой-то причине есть, то её решение известно и относительно несложно.
sci_nov
Ряд Фурье для периодических сигналов. Интеграл Фурье - для непериодических. Периодический сигнал имеет дискретный спектр, непериодический сигнал имеет непрерывный (сплошной) спектр.