Некоторое время назад я решил написать рекомендательную систему для фильмов. Подобные системы умеют предсказывать оценку фильма который пользователь не смотрел на основании его оценок других, ранее просмотренных фильмов.

Подготовка данных

Я буду рассматривать рекомендательные алгоритмы, основанные на методе «Коллаборативной фильтрации». Исходными данными для них является множество оценок фильмов, сделанных большим количеством пользователей. Подобные данные для фильмов можно найти, например, тут.

Но доступные публично данные обычно устаревшие, а также содержат относительно мало оценок. Я хотел больше и актуальнее.

Для этого я решил использовать данные из социальной сети Letterboxd. Letterboxd — это англоязычный аналог Кинопоиска, где люди пишут рецензии и проставляют оценки просмотренным фильмам. У Letterboxd есть API, но на доступ к нему нужно подавать заявку. Я подал, но ответа так и не получил. Впрочем, оказалось, что необходимые данные легко получить с помощью веб‑скрейпинга, благо нет никаких лимитов на запросы к их серверу, как и других ухищрений. В результате у меня оказался набор данных, состоящий из примерно 15M оценок, сделанных 21K пользователями относительно 21K фильмов. Letterboxd использует оценки по 5-бальной шкале (0.5–5). Я считаю 10-балльную шкалу более привычной, поэтому буду просто удваивать 5-балльные оценки.

Сначала все оценки случайно делятся на две неравные группы:

• Trainset — бОльшая группа (обычно 80–90%) — группа оценок, на которой происходит обучение модели (нейронной сети).

• Testset — меньшая группа (обычно 10–20%) — группа оценок, на которой происходит проверка результатов работы модели.

То есть на этапе обучения модель не будет «знать» о некоторых оценках, и именно их мы будем использовать для проверки точности предсказаний модели.

Подготовленные данные можно скачать с Dropbox здесь.

Внутри архива 4 файла:
data_movies1.json - набор оценок для обучения (Trainset)
data_movies2.json - набор оценок для проверки (Testset)

формат файлов:
[
[
0, - индекс пользователя
3, - индекс фильма
9 - оценка
],
...
]

users.json - информация о соответствии индекса пользователя с id на letterboxd
[
{
"id": "00000", - id на letterboxd
"num": 0. - индекс пользователя
},
...
]

films.json - информация о соответсвии индекса фильма с id и url на letterboxd
[
[
"426406", - id на letterboxd
0, - индекс фильма
"parasite-2019" - фрагмент url страницы фильма
],
...
]

Обработка данных

Здесь можно посмотреть код описываемый в этой статье. Чтобы запустить самостоятельно - сначала загрузите файл data_movies.zip. Также крайне рекомендуется подключать GPU (T4 достаточно). Не судите за не чистоту кода - код не для продакшена.

Для предсказания оценок фильмов я использовал три методики:

1. Усреднение.

   Большинство любителей кино знают, что такое рейтинг IMDB или рейтинг Кинопоиска. И если у фильма рейтинг больше 8, его точно стоит рассмотреть в качестве кандидата для просмотра. Если рейтинг больше 7, это также хороший кандидат для просмотра. Если же рейтинг меньше 6, то, скорее всего, фильм плохой. Такой рейтинг рассчитывается простым усреднением оценок всех пользователей сервиса для каждого фильма.

2. Метод Singular Value Decomposition (SVD).

   Это классический метод предсказания оценки. Можно почитать о нем, например, тут. Честно говоря, я не изучал, как он работает. Но для его использования достаточно написать три строки на Python с помощью библиотеки Surprise:

   algo = SVD()                      # создание 
   algo.fit(trainset)                # обучение 
   predictions = algo.test(testset)  # предсказание оценок тестовой группы

3. Нейросетевой метод (NN).

   Строится нейронная сеть следующей конфигурации:

   

   На входе — индексы фильмов и индексы пользователей, на выходе — оценка. Индексы сначала трансформируются в эмбеддинги размерности 64, а затем попадают на два dense‑слоя с 1024 нейронами каждый. Сеть содержит 3.8М обучаемых параметра.

А теперь сравним результаты:

1. Метод усреднения дает среднюю ошибку 1.28. То есть рейтинг Letterboxd (Кинопоиска, IMDB) предскажет оценку любого пользователя относительно любого фильма со средней ошибкой 1.28 по 10-бальной шкале.

2. Метод SVD дает среднюю ошибку 1.08

3. Метод NN дает среднюю ошибку 1.06

Вот так это выглядит на гистограмме:

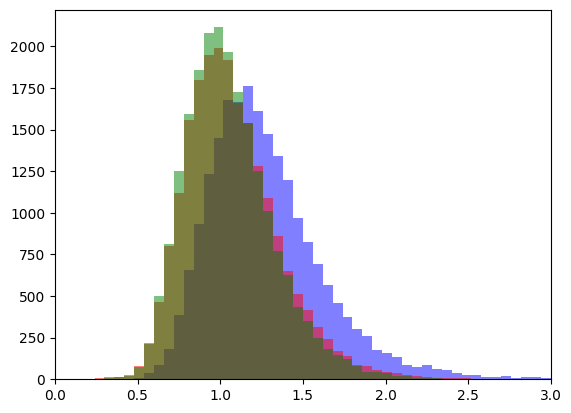
Видно, что оба рекомендательных алгоритма дают очень близкие результаты (красный и зеленый почти совпадают). Они также обеспечивают более точное предсказание оценки, чем простое усреднение. Но лучше они всего на 17 процентов!

Еще раз: персонализированные рекомендации алгоритмов дают лишь незначительное улучшение качества предсказания оценки фильма в сравнении с неперсонализированным усреднением. При этом инвестиции, которые нужно сделать пользователю, чтобы получить такие рекомендации, весьма значительны — нужно проставить осмысленные оценки паре сотен фильмов. В то время как усреднение (рейтинг Letterboxd/IMDB/Кинопоиск) дает универсальные результаты, работающие для всех пользователей!

Далее рассмотрим, какие рекомендации алгоритмы дают отдельному пользователю на моем примере (индекс пользователя = 15 122).
Результаты:

1. метод усреднения дает среднюю ошибку 1.56

2. метод SVD дает среднюю ошибку 1.62

3. метод NN дает среднюю ошибку 1.61

Видно, что усреднение предсказывает мою оценку хуже, чем среднему пользователю. И оба рекомендательных алгоритма дают результат хуже усреднения!

А вот как выглядит топ рекомендованных мне фильмов алгоритмом SVD (без удаления уже просмотренных!):

Spirit: Stallion of the Cimarron
Radio Rebel
PK
Bratz
The Sweetest Thing

Да, фильм PK я смотрел и люблю. Остальные же не вызывают сильного желания их немедленно посмотреть.

Топ рекомендаций алгоритма NN выглядит субъективно интереснее:

My Liberation Notes
Tokyo Olympiad
The Aerial
FEUD
The Future Diary

Учитывая, что из приведенных выше рекомендаций не были удалены уже просмотренные мной фильмы, то рекомендации выглядят мягко говоря странно. Можно, конечно, предположить, что фильм про Олимпиаду в Токио 1964 года после просмотра войдет в мой топ 10... но я что‑то сомневаюсь. Это еще более касается романтической комедии The Sweetest Thing... В топе рекомендаций ожидаешь увидеть всё же что‑то типа IMDB top 100...

Иными словами, еще одна проблема подобных алгоритмов — ненадежность топовых рекомендаций. А именно топовые рекомендации интересуют зрителей больше всего.

Почему алгоритмы работают так "плохо"?

Очевидно, дело в качестве оценок. И здесь не играет роли беспечность зрителей — сама по себе оценка фильма обладает изначальной неопределенностью. Восприятие фильма во многом зависит от внешних обстоятельств, настроения зрителя, компании и многих других факторов. Повторный просмотр одного и того же фильма может привести к совершенно новым впечатлениям. К тому же, фильмы — это сложные, длинные и разнообразные произведения, и различные аспекты фильма могут вызвать у зрителя противоречивые эмоции, что также влияет на «случайность» его оценки. Также для создания достаточной (для работы алгоритмов) базы оценок (например, 300 фильмов), обычному зрителю, который смотрит один‑два фильма в неделю, потребуется 3–6 лет. Когда все эти оценки будут сделаны, самые старые станут неактуальными из‑за неизбежного «дрейфа» вкусов зрителя.

Результаты моей работы, в частности, объясняют, почему кино‑рекомендательные системы не получили широкого распространения (попробуйте найти рекомендации на сайте Letterboxd... а они там есть!), зато все знают, что такое рейтинг Кинопоиска.

Возникает вопрос, почему, например, «работают» рекомендации музыки? Ответить на него не сложно. Лайк музыкального трека значительно менее случаен, чем «лайк» фильма. Трек короче. Он более однороден для восприятия. Средний пользователь прослушивает десятки треков ежедневно. И набор любимых треков может качественно представить вкус пользователя для работы алгоритма.

Резюме

Персонализированные рекомендательные алгоритмы в области кино оказываются только статистически (на бумаге) эффективнее простого усреднения. К тому же, они не обеспечивают надежности топовых рекомендаций, что что делает их не применимыми на практике.

Замечу, что я просмотрел много статей про алгоритмы для рекомендации фильмов, но ни в одной из этих статей я не видел сравнения результатов с простым усреднением — а это, на мой взгляд, впечатляет.

В следующей статье я опишу, как я придумал «композитный» рейтинг фильма и написал приложение для поиска фильмов с его помощью.