05.08.2023 10:30
Ultrageopro1966 30 3400 Источник

Введение

статья подготовлена UltraGeoPro

В данной статье будут рассмотрены способы анализа временных рядов. Разберем основные методы прогнозирования упорядоченных данных.

Простыми словами, временной ряд - это данные, упорядоченные по времени (например, курс доллара).
Анализ временных рядов позволяет находить основные закономерности в данных и прогнозировать их.

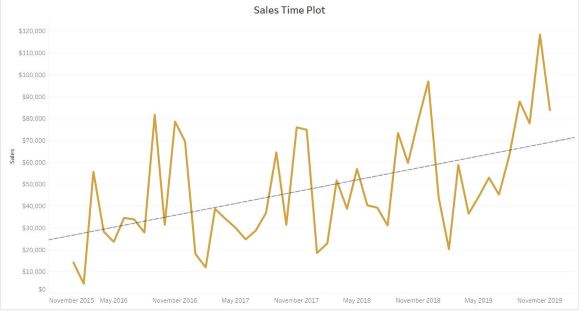
Пример временного ряда (зависимость продаж от времени)

На текущий момент было изобретено большое кол-во методов работы со структурированными данными, так что мы рассмотрим лишь некоторые из них на примере данных о погоде с 2013 года по 2017.

Обработка данных

Для анализа временных рядов и их прогнозирования будет использован язык Python в связке со сторонними библиотеками (pandas, numpy, tensorflow, matplotlib). Статья содержит достаточное кол-во визуализаций и пояснений для понимания ее содержания.

Загрузка датасета

# Импорт библиотек
from datetime import datetime

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

# Выгрузка данных из таблицы с тренировочными данными
train_data: np.ndarray = pd.read_csv("DailyDelhiClimateTrain.csv").values

# Выгрузка данных из таблицы с тестовыми данными
test_data: np.ndarray = pd.read_csv("DailyDelhiClimateTest.csv").values

Изображение первых строк тестовой таблицы:

Ссылка на таблицу

Нормализация данных

В этой статье для удобства мы рассмотрим только температуру, но вы можете взять любой другой столбец датасета. Или даже все сразу.

Естественно, ни одна модель не сможет понять, что значит строковое представление даты "2017-01-01", так что давайте приведем значения первого столбца к целым числам (кол-во дней с начала отсчета)

Функция перевода даты в кол-во дней от 2013-01-01 (самая первая дата в таблице):

def days_since_zero_date(date_str: str) -> int:
	# Преобразование строки в объект datetime
	date_format: str = "%Y-%m-%d"
	date_obj = datetime.strptime(date_str, date_format)
	
	# Нулевая дата
	zero_date = datetime.strptime("2013-01-01", date_format)
	
	# Вычисление разницы в днях
	delta = date_obj - zero_date
	days = delta.days
	 
	return days

Теперь переведем все даты в загруженных таблицах в дни и выведем результат:

# Применяем ранее определенную функцию ко всем датам датасета
train_data[:, 0] = np.vectorize(days_since_zero_date)(train_data[:, 0])
test_data[:, 0] = np.vectorize(days_since_zero_date)(test_data[:, 0])

train_data = train_data.astype("float")
test_data = test_data.astype("float")

print(train_data[0])
# Вывод - [0 10.0 84.5 0.0 1015.6666666666666]
# Видно, что все даты превратились в дни

Далее необходимо нормализовать данные по формуле (метод Z-Нормализация)

x_{i}' = \frac{x_{i} - \overline{X}}{\sigma_{x}}

Где:

  1. \overline{X} - среднее значение выборки

  2. \sigma_{x} - стандартное отклонение выборки

  3. x_{i} - ненормализованное значение

  4. x_{i}' - нормализованное значение

class Normalize:
	def __init__(self, data: np.ndarray) -> None:
		self.data: np.ndarray = np.copy(data) # Записываем копию данных
		
		# Вычисляем среднее по каждому столбцу
		self.__mean: np.ndarray = data.mean(axis=0)
		# Вычисляем стандартное отклонение по каждому столбцу
		self.__std_dev: np.ndarray = data.std(axis=0)
		
	def normalizeData(self) -> np.ndarray:
		# Возврат нормализованных даннах по формуле
		return (self.data - self.__mean) / self.__std_dev
		
	def DeNormalizeData(
		self, normalized_data: np.ndarray, axes: list[int] = [0, 1, 2, 3]
	) -> np.ndarray:
		# Денормализация днанных по указанной оси
		return normalized_data * self.__std_dev[axes] + self.__mean[axes]

# Нормализация температуры
train_normalize_class = Normalize(train_data[:, 1:])
train_data[:, 1:] = train_normalize_class.normalizeData()

В данном фрагменте мы создали класс, реализующий логику нормализации данных. В двух последних строках нормализовали обучающую выборку (кроме значений дней). Метод DeNormalizeData позволяет интерпретировать любые данные, полученные с помощью модели, в привычной нам форме.

Построим график температуры для наглядности.

# Создаем поле графика
fig, ax = plt.subplots(1, 2)

# Лимиты на осях
ax[0].set_ylim([-10, 40])
ax[1].set_ylim([-10, 40])

# Подписи осей
ax[0].set_ylabel("Темперетура")
ax[0].set_xlabel("День")
ax[1].set_xlabel("День")

ax[0].set_title("Нормализованная температура")
ax[1].set_title("Реальная температура")

# Сетка на осях
ax[0].grid()
ax[1].grid()

# Отображение нормализованных и ненормализованных данных
ax[0].plot(train_data[:, 1], c="b", linewidth=1)
ax[1].plot(
	train_normalize_class.DeNormalizeData(train_data[:, 1], axes=[0]),
	c="r",
	linewidth=1,
)

plt.show()

Видно, что нормализованные данные не потеряли свою информационную ценность, легко восстанавливаются в реальные данные (второй график) и более удобны для анализа с помощью моделей машинного обучения. О пользе нормализации

Сглаживание шума

Сглаживать шум будем методом скользящей средней. Суть метода в том, что мы проходимся по всему графику "окном" определенного размера. Перемещая окно, вычисляем среднее всех значений, которые в него попали. Таким образом мы сглаживаем весь шум графика, так как он компенсирует сам себя.
На самом деле, для решения нашей задачи применение данного метода не является обязательным, в статье он приведен скорее в образовательных целях

SMA_{t}=\frac{1}{n}\sum^{n-1}_{i=0}p_{t-i}

SMA_{t} - значение простого скользящего среднего в точке t
n - количество значений исходной функции для расчёта скользящего среднего (размер "окна")
p_{t-i} - значение исходной функции в точке t-i

Пример использования SMA (взято из интернета)

Реализация в коде с помощью pandas:

window_size = train_data.shape[0] // 70
denoised_data: np.ndarray = (
	pd.Series(train_data[:, 1])
	.rolling(window=window_size)
	.mean()
	.iloc[window_size - 1 :]
	.values
)

Результат:

Я не буду прикреплять код построения графика, так как ничего нового вы там не найдете.

Прогнозирование данных

Видно, что график температуры обладает ярко выраженной периодичностью и сильно напоминает синусоиду.
Из этого вытекает цель - подобрать наиболее подходящую синусоиду (или сумму синусоид), которая будет наилучшим образом соответствовать температуре.

Подбор подходящей кривой с помощью преобразования Фурье и градиентного спуска.

Преобразование Фурье

Преобразование Фурье - операция, которая сопоставляет первой функции вторую: вторая функция описывает коэффициенты («амплитуды») при разложении первой функции на элементарные составляющие — гармонические колебания с разными частотами. То есть фактически данное преобразование раскладывает функцию на сумму синусов разной частоты.

Формально преобразование определяется так:

G(t) = \int_{-\infty}^{\infty} g(t) e^{-2\pi ift} \, dt

Где f - исследуемый диапазон частот, а G(t) - амплитуда синусоиды частоты f, которая является слагаемым исходной функции.
Для более подробного ознакомления с концепцией преобразования Фурье советую посмотреть данное видео

Визуализация преобразования

Таким образом, если мы возьмем несколько синусоид максимальной амплитуды (те, которые лучше всего аппроксимируют наши данные) и построим график их суммы, то мы получим неплохую аппроксимацию температуры (в нашем случае).

Но, к сожалению, преобразование Фурье не выдает нам все веса идеальной функции, но и нам нужна только частота, ведь остальные параметры мы получим с помощью метода градиентного спуска. Но давайте по порядку и в коде:

# Значения на оси X (абсциссе), на основе которых модель будет делать предсказания
x_data:np.ndarray = np.linspace(0, len(denoised_data), len(denoised_data))

# Дискретное Преобразование Фурье, список амплитуд
mfft:np.ndarray = np.fft.fft(denoised_data)

# Получаем индексы частот, которые соответствуют самым значимым (с высокой амплитудой) синусоидам.
imax:np.ndarray = np.argsort(np.absolute(mfft))[::-1]

Для простоты мы будем раскладывать наши данные на сумму пяти синусоид. Не будем брать слишком много слагаемых, чтобы модель не потеряла обобщающую способность.

# Кол-во синусов, которые мы будем суммировать
number_of_sinuses: int = 5

# Берем первые number_of_sinuses самых высоких амплитуд (они соответствуют частотам)
imax = imax[:number_of_sinuses]

# Вычисляем частоту каждой синусоиды
frequency:np.ndarray = np.array(imax) / len(denoised_data)

Оптимизация параметров

Для начала определим функцию, которая будет аппроксимировать наши данные о температуре. Из-за того, что мы рассматриваем сумму пяти синусов, то определение нашей модели напрашивается само:

Y(w, x) = b + \sum_{i=0}^{4} w_{3i}\sin(w_{3i+1}x + w_{3i+2})

Теперь нужно инициализировать наши параметры так, чтобы их получилось верно оптимизировать (большинство моделей плохо оптимизируют параметры тригонометрических функций со случайно инициализированной частотой).

  1. Параметр w_{3i} будем инициализировать значением стандартного отклонения всей выборки (w_{3i} = \sigma_{x}).

  2. Параметр w_{3i+1} (самый важный) будем инициализировать полученной частотой (умноженной на 2\pi) для каждого синуса соответственно (w_{3i+1}=2\pi f_{i}). Это нужно сделать, чтобы модель не подбирала частоту волны, в противном случае параметры не будут оптимизированы.

  3. Параметр сдвига по абсциссе мы инициализируем 0

  4. Параметр b мы инициализируем математическим ожиданием выборки (b = \overline{X})

# Начальные параметры
init_params: np.ndarray = np.array(
	[
		np.array([np.std(denoised_data), frequency[i] * 2 * np.pi, 0.0])
		for i in range(number_of_sinuses)
	]
)

bias: float = np.mean(denoised_data)

Оптимизируем наши параметры путем градиентного спуска в связке с оптимизатором Adam. В качестве функции ошибки модели используем MSE.

Функция ошибки (MSE), которую наш алгоритм будет пытаться минимизировать

MSE = \frac{1}{n}\sum_{i=1}^{n}(y-\overline y)^{2}

y - реальное значение целевой переменной (метка)
\overline y - предсказание модели

Градиентный спуск
Градиентный спуск заключается в том, что по мере обучения модели мы вычитаем из каждого веса значение его локальной частной производной от функции ошибки. Данный алгоритм приводит к ее минимизации, то есть к наиболее точным ответам модели. Определение:

w_{n} = w_{n} - \frac{\delta E}{\delta w_{n}}\cdot \eta

E - функция ошибки
w_{n} - данный вес
\eta - коэффициент скорости обучения (чем больше, тем агрессивнее обучается модель, часто выбирают 10^{-3})

Оптимизатор Adam (необязательно для прочтения)
Идея Adam заключается в том, чтобы адаптивно изменять скорость обучения для каждого веса на основе двух моментов первого и второго порядков градиента. Веса с большим градиентом получают меньший шаг, а веса с меньшим градиентом получают больший шаг.

Оптимизатор работает по данному алгоритму:
m_t = \beta_1 m_{t-1} + (1 - \beta_1)g_t
v_t = \beta_2 v_{t-1} + (1 - \beta_2)g_t^2
\hat{m_t} = \frac{m_t}{1 - \beta_1^t}
\hat{v_t} = \frac{v_t}{1 - \beta_2^t}

Оптимизация весов:

w_t = w_{t-1} - \frac{\eta}{\sqrt{\hat{v_t}}+\epsilon} \hat{m_t}

Где:
t - номер итерации
w_t - вектор весов в момент времени t
g_t - вектор градиентов в момент времени t
m_t - оценка первого момента (среднего значения) градиента в момент времени t
v_t - оценка второго момента (среднего квадрата) градиента в момент времени t
\beta_1 и \beta_2 - параметры, обычно равные 0.9 и 0.999 соответственно
\eta - скорость обучения
\epsilon - малое число, используемое для стабилизации деления

Пример поиска минимумов функции методом градиентного спуска

Модель

Создадим модель с помощью библиотеки tensorflow. Остальные популярные варианты (например, scipy) представляют скудные возможности для определения и визуализации обучения, так что напишем собственную модель и обучим ее.

Важно! Так как оптимизатор Adam обладает стохастической природой, нужно выполнить команду tf.random.set_seed(), чтобы все, кто запустит код получили одинаковые результаты.

Определение функционала модели и ее параметров (с помощью keras.layers.Layer)

# Импорт модулей
import tensorflow as tf
from keras import layers
from keras.optimizers import Adam

tf.random.set_seed(8)

# Определяем слой
class SinLayer(layers.Layer):
	def __init__(self): # Инициализируем методы и атрибуты родительского класса
		super(SinLayer, self).__init__()
		
	def build(self, _): # Задаем начальные параметры
		self.kernel = self.add_weight(
			"kernel", shape=(number_of_sinuses, 3), trainable=True
		) # Веса модели
		
		# Свободный коэффициент
		self.bias = self.add_weight(name="bias", shape=(), trainable=True) 
		
	def call(self, inputs): # Реализация функционала нашей модели (ранее в статье)
		result: float = 0
		for i in range(number_of_sinuses):
			result += self.kernel[i][0] * tf.sin(
				self.kernel[i][1] * inputs + self.kernel[i][2]
			)
		return result + self.bias # Результат работы модели

Теперь определим саму модель и скомпилируем ее:

# Определение модели
model = tf.keras.Sequential(
	[
		layers.Input(shape=(1,)),
		SinLayer(),
	]
)

# Компилируем модель оптимизатором Adam (с наиболее подходящими параметрами)
# и ошибкой MSE
model.compile(Adam(0.001, 0.8, 0.9), "mean_squared_error")

# Задаем модели ранее определенные веса для правильной оптимизации весов
model.set_weights([init_params, bias])

Теперь обучим нашу модель на тренировочных данных и построим график изменения ошибки по мере обучения.

# Получаем историю ошибки модели
history = model.fit(x_data, denoised_data, epochs=70)

# Отображаем ее на графике
plt.plot(history.history["loss"])
plt.grid()
plt.xlabel("Эпоха")
plt.ylabel("Значение ошибки MSE на данной эпохе")
plt.show()

Эпоха — это количество полных прохождений всего датасета. Чем больше эпох, тем лучше натренирована нейросеть.

Видно, что ошибка модели сильно уменьшилась, значит, она натренировалась

Важное замечание! К ответу регрессионной модели принято добавлять случайный шум (мы тоже так будем делать):

y = Y(w, x) + \epsilon

Теперь посмотрим, как наша модель предсказывает данные тренировочной выборки. Для этого также построим график (но перед отображением нужно обязательно денормализовать данные с помощью ранее определенного метода DeNormalizeData):

Видно, что наша модель успешно уловила все тренды и периодизацию. Хороший результат.

Вычисление ошибки модели на тестовой выборке

Для вычисления ошибки модели будем использовать функцию MAE:

MAE(y, \overline{y}) = \frac{1}{n}\sum\mid y-\overline{y}\mid

Фактически, данная ошибка - среднее отклонение предсказанных данных от действительных.

Вычислим ошибку на тестовой выборке (на денормализованных, реальных данных):

# Определяем функцию ошибки
def MAE(predictions: np.ndarray, labels: np.ndarray) -> float:
	return np.mean(np.abs(predictions - labels))

# Выводим значение ошибки
print(
	MAE(
		train_normalize_class.DeNormalizeData(
			model(test_data[:, 0]).numpy().T[0], axis=[0]
		) + np.random.normal(size=test_data[:, 0].shape),
		test_data[:, 1],
	)
)

Мы выполняем преобразование data.numpy().T[0] из-за того, что модель выводит тензор Tensorflow формы (114, 1). Данное преобразование переводит ответ модели в вектор numpy и выделяет 114 элементов, которые являются ответом

После выполнения кода ошибка модели составила 2.2743354568119476 градусов цельсия. То есть наша регрессионная модель предсказывает температуру на 114 дней (длина тестовой выборки) вперед с погрешностью чуть более 2 градусов.

Важно заметить, что данная модель - лишь пример, который был приведен в целях указать на возможные способы поиска периодизации и трендов в данных. Если у вас есть структурированные данные, не такие сложные как погода, то описанный в статье метод может оказаться более чем эффективным. Но в случае с погодой, естественно, правильным будет обращаться за помощью к метеорологической службе.

Заключение

Кроме методов, рассмотренных выше, существует множество различных способов анализировать и прогнозировать временные ряды. К ним относятся нейросети и прочие математические приемы.

Материалы из статьи:

Тем, кому интересна концепция прогнозирования временных рядов, могу посоветовать:

Комментарии (30)


  1. economist75
    05.08.2023 15:47
    #0
    +4

    Нет неудовлетворительных методик прогноза, есть лишь дефицит достоверных данных.

    Парадокс нынешней ситуации в том что в некоторых узких областях - данных уже достаточно, но публичные анализы/прогнозы по ним нежелательны, т.к. это многим перекроет традиционные и очень большие доходы (бигфарма, фитнес, госзакупки итд). Поэтому эти сферы прилагают титанические усилия по дезавуированию возможностей, плодят дезу, ангажируют журналистику, инфлюэнсеров, блогосферу. ChatGPT также участвует в правдоподобной лжегенерации "фактов" и он превратит Интернет в помойку и вызовет серьезный системный кризис, когда человечество обязано будет договориться считать честно. Ну а пока нужно, как в статье, тренироваться в любых, даже шаровых прогнозах, это нетривиальная, полезная и интересная задача. Появятся чистые данные - смысл этих прогнозов многократно возрастет.


  1. Spaceoddity
    05.08.2023 15:47
    #25826436
    -1

    Ничего не понял... Погода (долгосрочный прогноз) - это же абсолютно "не экстарполируемое" явление. Слишком много вводных. Эдакая "задача трёх тел на максималках"))


    1. Ultrageopro1966 Автор
      05.08.2023 15:47
      #25826512
      +2

      Естественно, поведение трех тел - абсолютно непредсказуемое явление. В случае с погодой, из-за того, что мы живем на Земле, которая, в свою очередь, двигается вокруг Солнца, мы можем наблюдать периодизацию и тренды, которые всегда будут присутствовать. Я думаю, когда вам говорят слово зима, вы представляете холод, а когда лето - тепло. Тем не менее, погоду нельзя предсказать без погрешности, но с точностью до нескольких градусов - можно. На данный момент существуют методы прогноза климата, которые делают на несколько лет вперед. Они могут предсказать среднюю погоду с довольно небольшой ошибкой.


      1. Lazytech
        05.08.2023 15:47
        #25826542

        Насколько я понимаю, если речь идет о климате, точно прогнозировать более-менее можно уже свершившиеся факты, а с будущим, да еще и на несколько лет вперед, - как карта ляжет... Конечно, утрирую, но все-таки.


      1. Spaceoddity
        05.08.2023 15:47
        #25826666

        Давайте я вам для начала на пальцах. Весной Вильфанд Р. М. заявил что лето в моём регионе будет не просто жарким, а рекорды бить начнёт. В итоге весь июль лили дожди. Ну вон там циклон какой-то европейский застрял (почему-то у гидрометцентра хорошо получается давать названия всяким циклонам и объяснять погоду постфактум). На начало августа стали давали прогнозы что всё позальёт. В итоге +34 стоит. Окей, у них там "67% достоверность долгосрочных прогнозов"... Понадобились мне тут краткосрочные прогнозы - я уже не читаю, я карты смотрю с движениями воздушных масс на день-два - всё мимо! Вот просто зла не хватает! Начинаешь сомневаться вообще в целесообразности существования этой службы...

        Температура воздуха зависит ведь не только от наклона земной оси)) Она очень сильно зависит от движений воздушных масс (которые могут формироваться и двигаться крайне рандомно - там же всё по цепочке, одно за другое цепляется и выливается в итоге в некую "сингулярность"), а ещё "бонусом" идёт хозяйственная деятельность человека - это вы тоже учитываете?)) Это же не экстраполируется - тут вам и экспоненциальная, и степенная функции.

        Ну а то, что вы описали... Ну да, ряды динамики из вузовского курса статистики. Есть аналитический способ экстраполяции рядов динамики. Но в вашем случае у вас же совершенно недостаточно данных! Тут можно вообще ничего не экстраполировать, а просто брать среднюю температуру прошлого года и ориентироваться на неё - в озвученные вами пределы вложимся))

        И это я ещё молчу про ряд вообще немоделируемых факторов, как то: https://ru.wikipedia.org/wiki/Год_без_лета

        Возьмёт какой-нибудь Йеллостоун бахнет и привет всем прогнозам)) Экстремальный случай? Ну пожалуй. Но тогда мне в голову приходит довольно бородатый анекдот из ТБВ: "У меня есть решение, но это работает только для сферических цыплят в вакууме"


        1. Ultrageopro1966 Автор
          05.08.2023 15:47
          #25826832
          +1

          Во-первых, я уже сказал, что данная статья лишь описывает возможные примеры анализа временных рядов.

          Во-вторых, экспоненциальные и степенные функции также раскладываются на ряды гармонических колебаний, так что данный метод в состоянии учесть такие зависимости.

          В-третьих, я согласен, что погода зависит от многих факторов, в том числе в данных о температуре всегда присутствует случайность (как и в большинстве других временных рядах, что делает невозможным сделать точный прогноз). Но из-за того, что температура зависит от определенных факторов, большинство из которых несет периодичный характер, мы можем сделать приблизительный прогноз на несколько месяцев вперед за счет разложения данных на гармонические колебания. https://byjus.com/free-ias-prep/ncert-notes-factors-controlling-temperature-distribution/. Факторы места рассматривать бесполезно, ведь с течением времени данное место не меняется. Для того чтобы учесть наибольшее кол-во факторов без потери обобщающей способности модели, мы раскладываем данные на сумму нескольких синусоид. Если бы погода зависела только от положения земли, то нам хватило бы одной.

          Как я писал в статье, нам нужно создать обобщающую и усредняющую модель, цель которой не предсказать погоду на завтра, а оценить возможную температуру на следующие несколько месяцев с наименьшей погрешностью. Подобные задачи решаются методом, который я привел в тексте, что уже делает данную работу небесполезной.

          В любом случае, если вы посчитаете ошибку предложенной вами модели ("просто брать среднюю температуру прошлого года и ориентироваться на неё "), то она получится в разы больше чем у модели, предложенной мной.

          Предлагаю не акцентировать внимание на сути датасета, а посмотреть на то, как модель способна аппроксимировать данные из него. Все вычисления говорят сами за себя.

          Спасибо за ваш комментарий.


          1. Spaceoddity
            05.08.2023 15:47
            #25826902
            +1

            Да все уже поняли о чём ваша статья.

            Считайте вашу необходимость объяснять это каждому комментирующему - наказанием за кликбейтный заголовок))


        1. economist75
          05.08.2023 15:47
          #25827116
          +4

          Нет неудовлетворительных методик прогноза, есть лишь дефицит достоверных данных.

          Парадокс нынешней ситуации в том что в некоторых узких областях - данных уже достаточно, но публичные анализы/прогнозы по ним нежелательны, т.к. это многим перекроет традиционные и очень большие доходы (бигфарма, фитнес, госзакупки итд). Поэтому эти сферы прилагают титанические усилия по дезавуированию возможностей, плодят дезу, ангажируют журналистику, инфлюэнсеров, блогосферу. ChatGPT также участвует в правдоподобной лжегенерации "фактов" и он превратит Интернет в помойку и вызовет серьезный системный кризис, когда человечество обязано будет договориться считать честно. Ну а пока нужно, как в статье, тренироваться в любых, даже шаровых прогнозах, это нетривиальная, полезная и интересная задача. Появятся чистые данные - смысл этих прогнозов многократно возрастет.


          1. Ultrageopro1966 Автор
            05.08.2023 15:47
            #25827122

            Полностью с Вами согласен, спасибо за комментарий.


      1. omxela
        05.08.2023 15:47
        #25827560
        +1

        На данный момент существуют методы прогноза климата, которые делают на несколько лет вперед. Они могут предсказать среднюю погоду с довольно небольшой ошибкой.

        Возможно, и существуют. Всегда хочется верить в чудо. Но при чем тут данная статья? Прогнозирование временнЫх рядов методом суммирования некоторого количества частотных гармоник старо, как мир. Когда встречаю очередную заметку, где с энтузиазмом вот это излагается, всегда ищу одну обязательную оговорку. Это относится к стационарным последовательностям, статпараметры которых либо вовсе не меняются во времени, либо меняются достаточно плавно, "адиабатически". Например, глобальная средняя температура на поверхности земли является параметром стационарным. Как справедливо отмечает ТС, зимой относительно холодно. Летом - относительно тепло. Но мы что, именно это предсказываем с высокой точностью? Локальные климатические параметры существенно нестационарны. Причина тому - глобальная связность и изменчивость климатической системы. То, что Земля за год получает от Солнца одно и то же количество энергии (примерно), локально не значит ничего. Поэтому так провально промахиваются даже относительно короткие и даже качественные прогнозы на данный регион. Например, весной гидрометцентр плохо предсказывает предстоящее лето в Москве даже в терминах "сухое-мокрое" и "жаркое-прохладное", хотя оперируют они далеко не такими примитивными вещами, как суммирование нескольких синусоид.


      1. dgoncharov
        05.08.2023 15:47
        #25828406

        Да, вот про зиму и лето как раз есть вопросик. Вы нормализуете данные, переводя их в число сигм от среднего. Уместно ли брать среднее по всему датасету, если средняя температура летом и зимой разная?


  1. Lazytech
    05.08.2023 15:47
    #25826464
    +3

    Прочитав статью, вы узнаете, как можно прогнозировать погоду с точностью до двух градусов на 3 месяца вперед <...>

    Не верю! (с)

    Прогнозы погоды стали намного точнее. Как в метеорологии произошла тихая революция?
    ЦИТАТА:

    Прогнозировать погоду сложно, прежде всего, из-за того, что земная атмосфера хаотична. Математики вкладывают в это слово не тот смысл, что обыватели. «В хаотической системе растет доля ошибки, если есть неопределенность в начальных данных, а она есть всегда хотя бы потому, что измерения проводятся с некоторой точностью: допустим, температура известна до десятых долей градуса. Насколько бы хорошей ни была погодная модель, она даст ошибку», — объясняет Александр Чернокульский, старший научный сотрудник лаборатории теории климата Института физики атмосферы им. А.М. Обухова РАН.

    Раздел математики, изучающий хаотические системы, и появился-то во многом из-за прогнозов погоды. В начале 1960-х годов американский метеоролог Эдвард Лоренц повторно прогнал данные через компьютер и получил совсем не такой результат, как в первый раз. Причина была в том, что сначала вычисления производились с точностью до шестого знака после запятой, а потом — только до третьего. Оказалось, что разница между тысячными и миллионными долями имеет огромное значение.

    Настолько разные решения уравнений так удивили Лоренца, что он поэтично заключил: «Единственный взмах крыла чайки способен изменить погоду навсегда». Позже коллеги посоветовали заменить чайку на более изящное животное, и чувствительность хаотической системы к начальным условиям получила название «эффект бабочки».

    Ошибки при расчетах будущих состояний атмосферы и других хаотических систем со временем накапливаются, поэтому прогноз погоды на сутки вперед значительно лучше, чем на месяц. Тем не менее точность постепенно растет: современные пятидневные прогнозы так же хороши, как сорок лет назад — однодневные. Полезный прогноз можно сделать и на девять-десять дней. А предел предсказуемости классическими моделями, по словам Александра Чернокульского, составляет две недели.


    1. Ultrageopro1966 Автор
      05.08.2023 15:47
      #25826538

      Пожалуйста, прочитайте статью, или проведите расчеты самостоятельно. Дело в том, что моя модель основывается лишь на данных прошлых дней, а предсказания метеорологов - на гораздо большем кол-ве факторов. Метеорологи могут предвидеть неожиданные скачки температуры и других показателей, когда моя модель - нет. Она скорее усредняет все показатели, находит тренды и периодизацию и на их основе делает прогноз. Тем не менее, Вы можете убедиться в верности расчетов самостоятельно.

      Также важно заметить, что ошибка вычислялась путем усреднения. То есть моя модель может сказать, что завтра будет 15 градусов, а на самом деле окажется 30. Но из-за большого кол-ва измерений ошибка усредняется и оказывается небольшой. Так что вы абсолютно правы в том, что такую модель использовать (в реальных целях) будет некорректно. Пример с температурой был приведен скорее в целях указать на возможные способы поиска периодизации в данных. Точно так же делают и эксперты из команды tensorflow, если это Вам о чем-то говорит.


      1. Lazytech
        05.08.2023 15:47
        #25826546
        +2

        В данной статье будут рассмотрены способы анализа временных рядов и применение их на практике. <...>

        Насколько я понимаю, описанные вам прогнозы погоды (точнее, температуры) практической пользы не имеют?


        1. Ultrageopro1966 Автор
          05.08.2023 15:47
          #25826558

          Ответ на этот вопрос не был целью исследования. Тем не менее, советую полагаться на предсказания метеорологов. Опять же, пример с температурой был приведен скорее в целях указать на возможные способы поиска периодизации в данных. То есть, если у вас есть структурированные данные, не такие сложные как погода, то описанный в статье метод может оказаться более чем эффективным.


          1. Lazytech
            05.08.2023 15:47
            #25826568

            Наверное, в качестве примера актуальнее было использовать курс доллара или евро...


            1. Ultrageopro1966 Автор
              05.08.2023 15:47
              #25826578

              Спасибо за отзыв.

              Нет, потому что курс доллара и евро напрямую зависит от новостей в мире, которые нельзя предсказать дальше, чем на пару дней. Пожалуйста, посмотрите на курс любой валюты и убедитесь в этом сами.


              1. omxela
                05.08.2023 15:47
                #25827578
                +2

                Угу. На языке статистики, повторюсь, эта "зависимость от новостей" приводит к нестационарности соответствующих временнЫх рядов. С погодой в данном регионе в этом смысле всё гораздо хуже.


              1. mikko_kukkanen
                05.08.2023 15:47
                #25831064

                Курсы валют и акций зависят от макроэкономических новостей на достаточно длительных отрезках времени - месяцы и годы. На средних сроках вполне нормально работает технический анализ, потому что в процессе участвуют трейдеры - простые люди. Только колебания совсем не периодические, поэтому никаких синусов там не найти. Кстати, если хотите предсказать динамику фондового рынка на десятилетия, то это совсем просто - будет устойчиво расти.


    1. GospodinKolhoznik
      05.08.2023 15:47
      #25828252

      Всё так. Но есть области более хаотичные чем другие и менее хаотичные в плане расчета погоды на несколько дней вперёд. Регионы у моря относительно предсказуемы, т.к. большая масса воды работает как термостат к тому же ветра ведут себя более предсказуемо - дуют с моря либо на море в зависимости от времени суток. Т.е. атмосферные условия ветер, температура, давление и влажность меняются в течении суток достаточно сильно, но меняются они относительно предсказуемо, и моделирование погоды получается более менее точным. А вот в великой степи средней полосы России ветра гуляют как хотят и прогнозировать погоду тут очень сложно.


      1. Lazytech
        05.08.2023 15:47
        #25828266

        В моем дилетантском понимании, автор статьи прогнозирует пресловутую среднюю температуру по больнице. Точнее, даже не саму температуру, а скользящее среднее или что-то вроде этого. Хотя, возможно, оно кому-то надо...


  1. ChePeter
    05.08.2023 15:47
    #25826514
    +3

    Вообще-то вся эта периодичность определяется вращением Земли вокруг Солнца и своей оси.

    Вот там да, Фурье очень хорошо описывает такие системы. ( потому что они периодичные)

    Но вот

    Видно, что график температуры обладает ярко выраженной периодичностью и сильно напоминает синусоиду.

    Этот пассаж конечно же так себе, простоват.

    Вы не погоду предсказываете ( если не называть предсказаниями, что в январе в России зима), а положение Земли на орбите.


    1. Ultrageopro1966 Автор
      05.08.2023 15:47
      #25826550

      Вы правы, но зная точное положение Земли на орбите (и располагая только этими данными), вы не предскажете температуру. Положение Земли лишь определяет температуру. Так что данная модель скорее находит связь значения температуры и положения нашей планеты в космосе. В любом случае, пример с температурой был приведен скорее в целях указать на возможные способы поиска периодизации в данных. Точно так же делают и эксперты из команды tensorflow, если это Вам о чем-то говорит.

      Ответить


  1. diakin
    05.08.2023 15:47
    #25826574
    +3

    "Прошла зима, настало лето. Спасибо партии за это!" (с)


  1. Orbit67
    05.08.2023 15:47
    #25826812

    Интересный факт, что предсказания цыганок сбываются чаще, чем предсказания синоптиков.


    1. Alexey2005
      05.08.2023 15:47
      #25827642

      Когда речь идёт о российских синоптиках — да. Потому что они окончательно оптимизировались и вместо того, чтоб строить прогнозы, попросту покупают чужие (иностранные) данные без малейших попыток их как-то осмыслить и скорректировать под местные реалии.
      Когда для какой-либо местности прогноз можно улучшить банальной корректировкой на константу — это явный признак профнепригодности прогнозистов…
      Вообще, изобретение динамических моделей — это худшее, что случалось с российской метеорологией. После этого точность прогнозов упала катастрофически, потому что собственных российских моделей нету, а иностранные оптимизированы в первую очередь для западной Европы, и для российской территории работают по остаточному принципу с весьма низкой точностью.
      А ещё в России очень любят всё секретить на ровном месте. Так, для этих территорий вам будет крайне сложно получать оперативные данные с доплеровских радаров или "живые" снимки с российских метеоспутников, потому как всё засекречено.


      1. Dynasaur
        05.08.2023 15:47
        #25827736
        +1

        Я всё лето внимательно слежу за прогнозами на Гисметео и Яндекс.погода по тому, что летом люблю купаться и хочу заранее спланировать в какие дни поеду купаться. Так вот претензий к точности прогнозов а пределах недели почти не было.

        Так что иногда надо меньше заниматься логическими построениями, а чаще смотреть в окно.


        1. Spaceoddity
          05.08.2023 15:47
          #25827784

          https://habr.com/ru/articles/752662/comments/#comment_25826666


    1. Dynasaur
      05.08.2023 15:47
      #25827716
      +1

      А можно это факт где-то увидеть в виде конкретных данных? Что-то я подозреваю, что как только мы увидим данные, сразу увидим, что это никакой не факт.


  1. sturex
    05.08.2023 15:47
    #25833968

    Не читал всю статью, но глаза случайно зацепились за график со скользящей средней

    Выше в статье

    Скользящая средняя может выглядеть так, как у вас на графике только если у вас есть "заглядывание в будущее" окном усреднения. Что, очевидно, грубейшая ошибка.

    Видите, как оранжевая линия (скользящая средняя), как бы, "обгоняет" синию? Так и должно быть, если всё правильно сделано.


  1. bazilevichla
    05.08.2023 15:47
    #25835224

    Сидишь довольный, пишешь себе свой прогноз погоды, смотришь: "О, отлично, завтра должно быть градусов 28, можно поехать купаться". Выезжаешь утром на велосипеде на речку, а тебя накрывает ураган с градом...
    Я это не в претензию автору поста ни в коем случае, просто вспомнилось, как неделю назад у меня дома приключился подобный сюрприз (можете загуглить "ураган в Казани" и посмотреть), о котором нас не предупреждал ни яндекс, ни кто либо другой, наверняка умеющий в умные алгоритмы предсказания погоды)