Эта статья будет полезна энтузиастам машинного обучения, а особенно тем, кто интересуется применением ML в промышленности. Из текста вы узнаете, какие факторы должен учитывать сталевар при выплавке металла, а также о точках оптимизации металлургических процессов и подводных камнях в обучении ML-моделей для производства.

Ищем точки оптимизации

Процесс выплавки стали состоит из следующих этапов:

• Загрузка металлолома в дуговую сталеплавильную печь (ДСП).

• Плавление сырья до жидкого состояния.

• Окислительный период. Сталевары поддерживают высокую температуру и производят присадки материалов. Некоторые элементы расплава выгорают, в результате образуется печной шлак. Часть элементов (например, [Mn]) частично переходит из расплава в шлак.

• Слив расплава в печь-ковш. В процессе снова производятся присадки материалов для корректировки химического состава расплава. При этом часть печного шлака тоже может попасть в печь-ковш.

• Восстановительный период. В установке печь-ковш (УПК) поддерживается необходимая температура. Сталевары производят финальные присадки для корректировки состава стали.

• Выпуск плавки.

Небольшое отступление: основные проблемы, с которыми сталкивается рядовой сталевар при каждой плавке:

·       Разные начальные условия. Основная доводка происходит на УПК после ДСП. При этом химический состав и прочие параметры металла на выходе из ДСП могут сильно отличаться от плавки к плавке. Из-за этого для каждой плавки нужно подбирать уникальные присадки.

·       Разные марки стали. Новая марка — это новый диапазон элементов, в который необходимо попасть.

·       Нехватка времени. У сталеваров зачастую нет времени на раздумья, поскольку нужно выпустить как можно больше плавок за рабочую смену. Это напрямую увеличивает прибыль.

Чтобы получить металл с определенными характеристиками, сталевары выполняют присадки химических элементов и таким образом меняют состав расплава. Например, в марке Ст10 содержание [Si] должно варьироваться в диапазоне от 0,17 до 0,37%, [Mn] — от 0,35 до 0,65%, а [C] — от 0,07 до 0,14%.

Примеры присадок

• FeSiMn. Ферросиликомарганец, содержит [Mn] и [Si]

• FeSi. Ферросилиций, содержит [Si]

• УСМ. Углеродосодержащий материал, содержит [C]

При этом каждый сотрудник должен провести как можно больше плавок за смену (в среднем за 12 часов сталевар успевает выполнить 13–15 плавок). Но в погоне за скоростью даже опытные специалисты могут ошибаться и неэкономно расходовать сырье.

Это очевидная точка оптимизации. В составе стали может быть довольно широкий диапазон содержания химических элементов. Если стремиться не просто попасть в него, а целиться в минимальные пороговые значения, можно сэкономить присадочные материалы. Чтобы решить эту задачу, мы разработали для сталеваров рекомендательный сервис на базе ML-технологий.

Система рассчитывает, какие материалы и в каком минимальном объеме нужно добавить в расплав, чтобы получить сталь с заданными характеристиками. Расчет выполняется сразу после получения анализа химического состава расплава. Тем самым мы снижаем нагрузку на сталеваров и ускоряем процесс принятия производственных решений.

В 1953 году Эдвард Колин Черри из Имперского колледжа Лондонского университета экспериментально подтвердил, что в среднем человек может одновременно концентрировать внимание не более чем на шести объектах. Как думаете, сколько факторов нужно учитывать сталевару при выплавке металла?

Ответ на картинке:

Первое приближение

Чтобы рассчитать минимально необходимое количество добавочных материалов, нужно прогнозировать содержание химических элементов в расплаве. В качестве примера попробуем спрогнозировать содержание [Si].

Логично предположить, что если мы не предпринимаем с расплавом никаких действий, концентрация элемента не изменится.

Если же мы добавим в расплав присадку, содержащую [Si], концентрация элемента увеличится пропорционально добавке.

Теперь попробуем сопоставить прогноз по этой формуле с реальным значением [Si].

На первый взгляд все отлично — прогноз хорошо бьется с реальной химией, что подтверждает r2 (коэффициент детерминации, чем ближе значение к 1, тем лучше модель объясняет фактические данные). Мы прогнозируем высокое значение [Si] и видим его в реальности. Но что если вместо абсолютного значения мы посмотрим на прирост [Si] до и после добавки?

Согласно выведенному нами уравнению (гипотезе), прирост должен быть линейным: чем больше добавка, тем он выше.

Если бы гипотеза была верна, мы бы увидели на графике ровную линию под 45° (черный пунктир на рис. 2). На практике большая часть графика оказалась ниже этой линии, как будто часть добавочных материалов не до конца перешла в расплав. Более того, если попытаться линейно аппроксимировать точки на графике (серая пунктирная линия), мы увидим не только несоответствие 45° (коэффициент α линейного уравнения должен быть равен 1 при 45°, в нашем случае он равен 0,77), но и отрицательное смещение β, что также говорит о недоусвоении части материала. В чем же дело?

Переосмысляем подход

Оказалось, что задача скрывает сразу несколько подводных камней:

• Даже если вы не добавляете ничего в расплав и продолжаете поддерживать высокую температуру, химические процессы в нем не останавливаются. Часть [Si] будет выгорать, взаимодействуя с кислородом.

• Кремний из присадок тоже может частично выгореть, так и не усвоившись в расплаве.

• К моменту проведения химического анализа (замера) присадки могут не до конца усвоиться в расплаве.

Первые две проблемы имеют общий корень: часть [Si] уходит на раскисление металла.

Мы научили модель учитывать неусвоение и выгорание материалов и тем самым «закрыли» случаи, расположенные ниже черной линии (см. рис. 3). Осталось разобраться с кейсами выше.

Это случаи, в которых [Si] прирос больше, чем его было добавлено. Мы уже упоминали, что часть присадочного материала может не до конца усвоиться в расплаве к моменту проведения химического анализа. При этом неусвоенные элементы не исчезают, а прирастают чуть позже. Эта логика справедлива и для материала, добавленного до УПК (во время слива расплава в печь-ковш). Таким образом, часть [Si] с предыдущего шага дополнительно прирастает на рассматриваемом промежутке.

Остается подобрать коэффициенты, отвечающие за усвоение и выгорание, и задача решена. Но здесь мы столкнулись с новой проблемой. Коэффициенты для каждой плавки должны отличаться. От плавки к плавке уровень выгорания и усвоения материалов может заметно разниться, что хорошо видно на графиках (рис. 2 и 3). Для каждой точки можно подобрать бесконечное количество сочетаний коэффициентов и объяснить кейс с помощью выведенного уравнения. В конечном счете мы получаем линейное уравнение с двумя неизвестными… Что с этим делать? Корректировать модель.

Точнее и сложнее

Прирост элемента в расплаве в первую очередь зависит от количества введенного материала. Попробуем взять модель сложнее линейной (CatBoost) без явной аналитической формулы и обучить ее на основе всех параметров плавки с учетом количества введенного материала. В данном случае именно введенный материал будет управляющим параметром. В результате решение будет прогнозировать прирост элемента, основываясь не только на добавках, но и на других параметрах процесса.

При обучении на реальных данных такая модель находит в них неочевидные связи и дает более точный прогноз. Возникает логичный вопрос: почему мы сразу ею не воспользовались? Дело в том, что более сложная, но точная модель — это не всегда хорошо. В погоне за точностью можно потерять более важные показатели, например, интерпретируемость результата. Линейная формула, которая записывается в явном виде и близка к реальной физике процесса, будет в разы понятнее сталеварам. А нам будет проще проводить отладку такого решения. И снова вопрос: зачем тогда мы обучали эту модель?

Возьмем отдельную плавку и построим прогноз, варьируя управляющий параметр — количество введенного [Si]. Прогнозное значение должно увеличиваться пропорционально изменению параметра — именно это мы видим на графике (см. рис. 4).

Синяя линия — это прогноз модели. Налицо практически линейная зависимость от управляющего параметра. Более того, мы можем линейно аппроксимировать прогноз (серая пунктирная линия на графике).

Полученное линейное уравнение можно записать с помощью простой формулы. Ничего не напоминает?

Итак, нужные нам коэффициенты усвоения и выгорания для каждой плавки можно получить из аппроксимации прогноза более сложной модели. Задача решена!

Вместо заключения

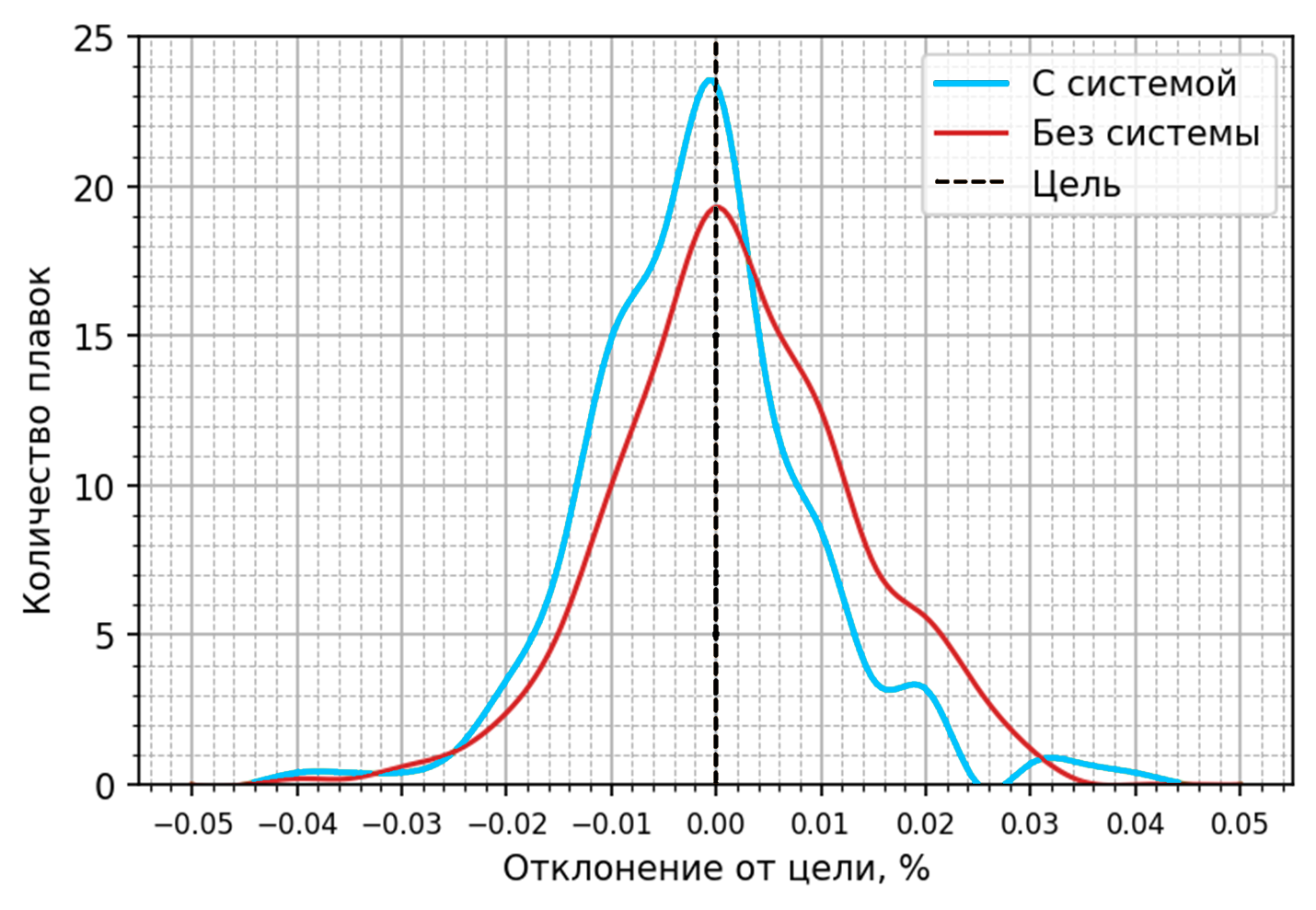
Разработанное нами решение не только снижает загрузку сталеваров, но и помогает заводу экономить сырье. При этом качество выплавляемой стали остается на прежнем высоком уровне.

• В основе решения лежит линейная модель. Благодаря этому результаты работы системы легко интерпретировать.

• Подход близок к реальной физике процесса.

• Более сложная модель позволяет увеличить точность прогноза, но не сильно влияет на интерпретируемость результатов.

Антон Головко, специалист машинного обучения "Инфосистемы Джет"