Всем привет! Меня зовут Евгений, я backend‑разработчик в компании Bimeister. Сегодня я хотел бы продолжить рассказ о нашем 3D движке Spatium. В статье речь пойдет еще об одном из алгоритмов оптимизации - поиске и удалении избыточных вершин из 3D моделей.

Материал может представлять интерес для инженеров, связанных с проектированием и разработкой в области 3D.

Контекст

В компьютерной графике геометрия может задаваться различными способами - списком граней, таблицей углов, вершинным или "крылатым" представлениями и т.д. Поэтому для работы с различными форматами моделей в едином пространстве сперва следует привести геометрии разных представлений к некоторому унифицированному описанию. Такое описание в общем виде представляет собой набор позиций вершин (точек в пространстве с тремя координатами x, y, z) и нормалей вершин (векторов с тремя компонентами x, y, z), сопоставленных с этими позициями. Если соединить три вершины отрезками, то получится треугольник. Этот треугольник графический процессор может либо закрасить каким-либо цветом, либо "натянуть" на него текстуру. А нормали нужны для правильного расчета отражений и теней при использовании света (без света мы ничего не увидим). Совокупность таких треугольников образует так называемый "меш" - фигуру, которая определяет форму многогранного объекта в пространстве.

Чем сложнее и детализированнее форма фигуры, тем больше вершин и треугольников, ее описывающих, она содержит. Дополнительное увеличение числа треугольников может быть вызвано тесселяцией или экспортом во внешний для среды моделирования формат. Во всех этих случаях может произойти так, что число треугольников в геометрии превысит минимальное количество, необходимое и достаточное для корректной отрисовки геометрии видеокартой. Это значит, что использование памяти на хранение информации будет увеличено, но данная информация никакой практической пользы нести не будет - на форму геометрии лишние треугольники, образованные избыточными вершинами, влияния не оказывают. Возникает желание эти избыточные вершины удалить, чтобы уменьшить потребление памяти на хранение, передачу и обработку этой геометрии. Для краткости такую оптимизацию будем называть "фильтрацией геометрии". Сразу сделаем оговорку о принципиальной разнице с другой оптимизацией, при которой из геометрии тоже удаляются вершины - упрощением. При упрощении форма геометрии меняется, а при фильтрации - нет.

Итак, под избыточными будем понимать такие вершины, удаление которых из геометрии не приведет к потере ее формы.

Кроме того, есть несколько ограничений:

1. Геометрия для нас - это два массива: массив координат вершин (позиций) и массив нормалей вершин. Поэтому работу ведем не просто с координатами, а с парами координата-нормаль. Если у нескольких вершин одинаковая координата (позиция), но нормали отличаются - для нас это разные вершины.

2. Вершины имеют матрицу трансформации. Нас будет интересовать компонент этой матрицы, отвечающий за масштаб.

3. В полигонах могут быть отверстия.

4. В результате оптимизации форма исходной геометрии должна сохраниться.

Наша оптимизация будет состоять из нескольких этапов. Далее рассмотрим каждый из них подробнее.

Этап 1 - Поиск и удаление вырожденных треугольников

Под вырожденными треугольниками будем понимать такие треугольники, у которых:

• Две или более вершины совпадают.

• Все три вершины расположены на одной прямой.

Зачем их искать? Вырожденные треугольники не определяют никакой формы, а память используют. Поэтому очищать геометрию начнем именно с них.

Вспоминаем про ограничения 1 и 2. Решим для себя, с какой приемлемой точностью позиционирования мы будем работать: для этого определим порядок характерных расстояний (мм, см, м, км). Если ваша предметная область - это заводы с размерами в сотни метров, то отрисовка треугольников с микронной точностью - явно избыточная (разница в 7-9 порядков).

Поэтому округляем до установленной величины с учетом масштаба, проверяем признаки вырождения, лишнее удаляем.

Этап 2 - Получение топологии геометрии

Топология геометрии понадобится для поиска различных участков, таких как границы полигонов, группы смежных треугольников и т.п.

Строим треугольники из пар позиция-нормаль. Затем для каждого треугольника:

• Вычисляем по правилу правой руки нормаль, уточняем ориентацию этой нормали по нормалям вершин.

• Строим ребра (нам важен хэш центра каждого ребра), запоминаем их.

После того, как все треугольники построены, наполняем словари "Вершина - Треугольники с этой вершиной" и "Треугольник - Смежные с ним треугольники". Они как раз пригодятся для разделения полигонов-кандидатов по областям смежности и определения их границ (ограничение 3).

Этап 3 - Поиск полигонов с потенциально избыточными вершинами

Поскольку форму геометрии изменять нельзя (ограничение 4), то будем работать с избыточными вершинами в рамках полигона. Полигоном будем считать набор треугольников, лежащих в одной плоскости.

Но сперва нужно найти подходящий полигон. Как это сделать? Вспоминаем, что у каждой вершины есть нормаль. Для любой точки плоскости нормаль будет одинаковой. Значит, нам нужно сгруппировать вершины по нормалям. Затем нужно проверить несколько условий:

1. Количество точек в группе должно быть больше трех (больше одного треугольника в плоскости).

2. Количество точек в группе должно быть кратно трем (геометрия в "сыром" виде, индексация вершин отсутствует).

3. Все точки в группе не должны принадлежать одной прямой.

4. Все точки в группе должны принадлежать одной плоскости - вершины могут иметь одинаковые нормали, но лежать в нескольких параллельных плоскостях с одинаковой ориентацией в пространстве.

Кроме того, даже располагаясь в одной плоскости, вершины с одинаковыми нормалями могут принадлежать разным полигонам. Поэтому нужно их разделить по "областям связности" - треугольникам со смежными ребрами.

Предварительно можно сгруппировать по нормалям сами треугольники, а группировку вершин по нормалям проводить уже внутри группы треугольников.

Те группы вершин, которые удовлетворяют всем перечисленным условиям, становятся полигонами-кандидатами на прохождение фильтрации. Отправляемся дальше.

Этап 4 - Поиск и удаление избыточных вершин

Для каждого полигона-кандидата нужно найти вершины, которые образуют границы полигона: внешнюю (оболочку) и внутренние (отверстия).

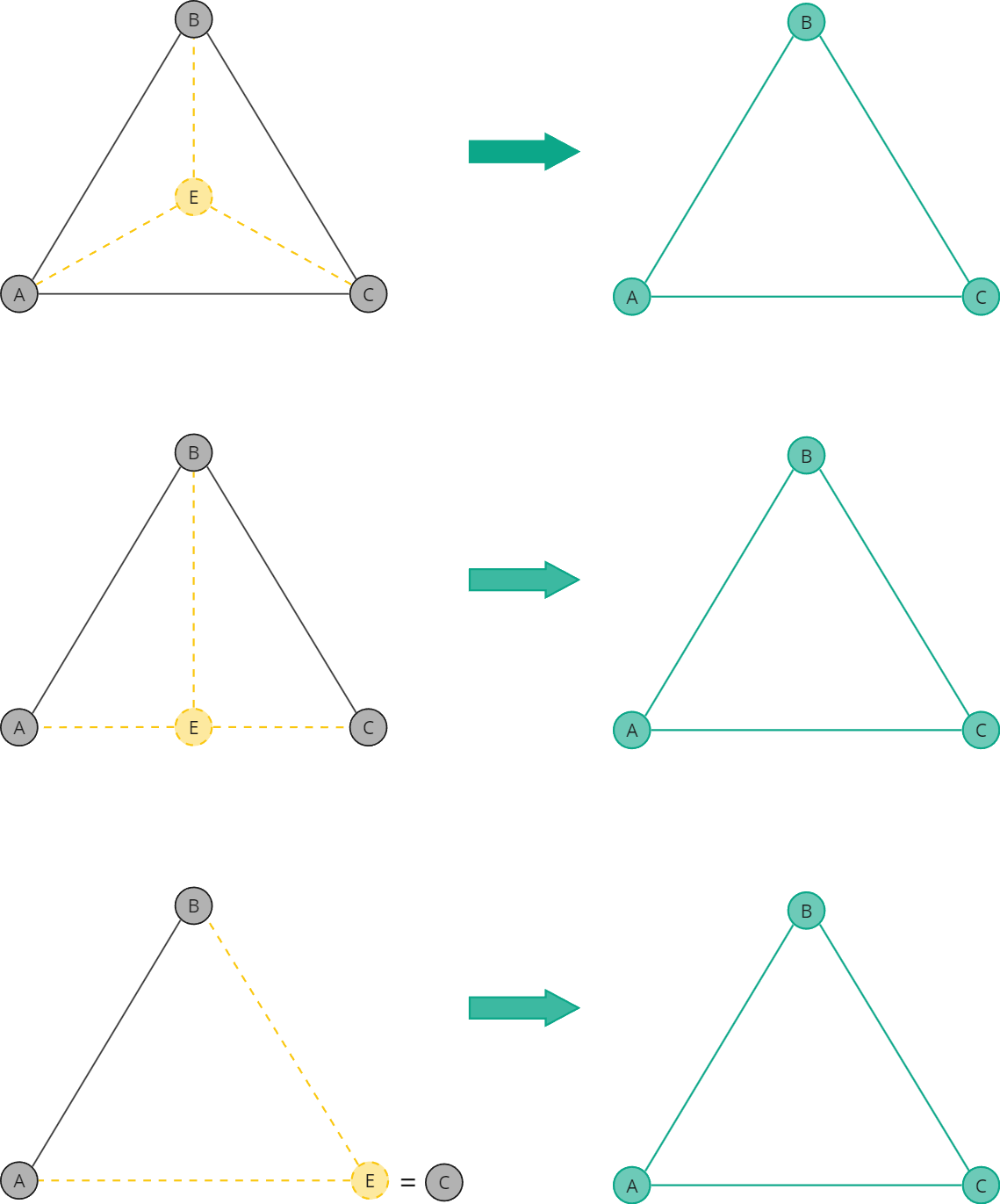
Вершины, которые не попали в список граничных, считаем избыточными - они расположены в "теле" полигона и не несут полезной информации о его форме.

А для граничных вершин строим отрезки, которые проверяем на принадлежность прямой. Если таких позиций больше двух, то избыточными будут позиции "внутри" отрезка - они тоже ничего не говорят о форме полигона.

Этап 5 - Ретриангуляция очищенных полигонов

Поскольку видеокарта работает с треугольниками, после удаления вершин полигон нужно снова превратить в набор треугольников, т.е. - триангулировать.

Поскольку мы имеем дело с полигонами, у которых могут быть отверстия, то нужно не забыть это учесть. Подходящим для нас алгоритмом будет триангуляция Делоне в ограничениях - граничные ребра будут учтены и не потеряются (неплохой визуальный пример здесь).

Ура! Полигон очищен, заново триангулирован и готов отправиться в видеокарту. Осталось только удалить все вхождения найденных избыточных вершин из исходной геометрии, после чего добавить в нее новые данные из триангуляции. Готово, можем сохранять меш и использовать вместо исходного.

Заключение

Удаление избыточных вершин с сохранением формы - это алгоритм, который может быть полезен, если ваша система работает с большим количеством неоптимизированных геометрий, которые нельзя упрощать.

Мы проводили исследования его эффективности на моделях нашей предметной области, спроектированных в САПР. Согласно результатам, для таких моделей данная оптимизация может быть весьма затратной по мощностям и времени (особенно для больших геометрий в несколько миллионов вершин), а итоговый эффект достаточно низкий - избыточными определяются менее 0.5% от всех вершин. Как правило, это центр круга (рисунок 5, сверху).

Возможно, что для моделей, полученных другими способами (сканирование, художественное моделирование, многоэтапная конвертация и т.п.) эффект будет более выраженным, но такие исследования мы не проводили.

Поэтому принимать решение о том, использовать данный алгоритм или нет - нужно индивидуально для каждого проекта, ориентируясь на предварительную оценку количества "пустых" данных в моделях конкретной предметной области.