Привет, GT! Сегодня поговорим об одном необычном состоянии света и о его не менее необычных применениях. Добро пожаловать под кат.
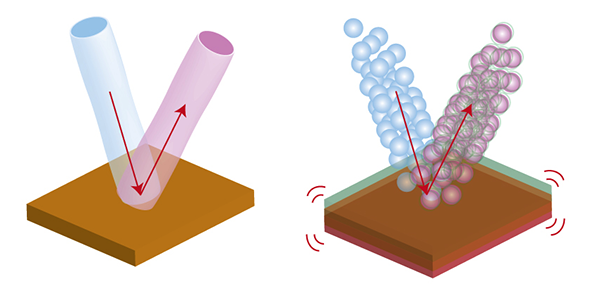
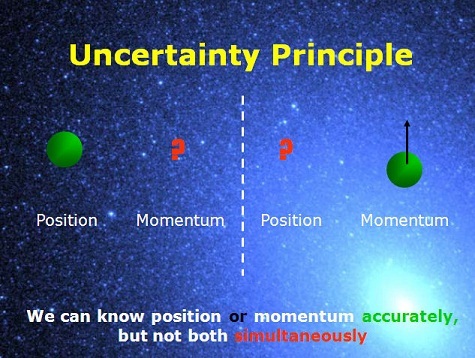
Соотношение неопределенностей Гейзенберга запрещает одновременно измерить координату и скорость (импульс) частицы. При этом никто не мешает точно померить одну из величин – но тогда неопределенность второй станет еще больше.
Вообще соотношения неопределенностей встречаются в физике довольно часто. Например, такое же соотношение верно для электромагнитной волны: оно связывает ее интенсивность (= число фотонов) и фазу:
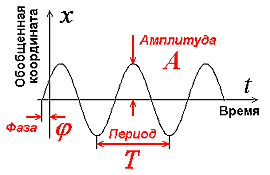
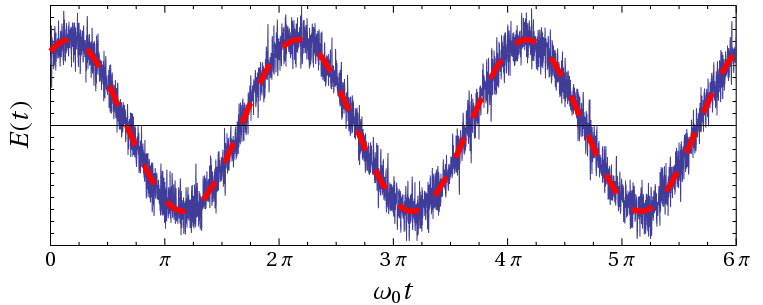
Из-за этой неопределенности мы не можем точно измерить описываемую волной синусоиду, для наблюдателя она всегда будет в шумовой дымке:
Это можно наглядно показать на круговой диаграмме, где амплитуде соответствует радиус до точки, фазе – угол между направлением на точку и осью Х. Зеленым показана неопределенность:
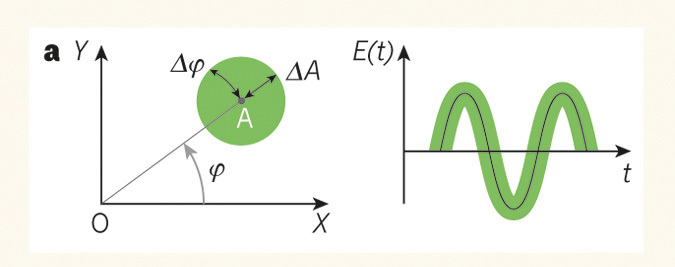
При этом никто не мешает точно определить либо амплитуду, либо фазу. Тогда кружок погрешностей превратится в эллипс, сжавшись в одном направлении и вытянувшись в другом:
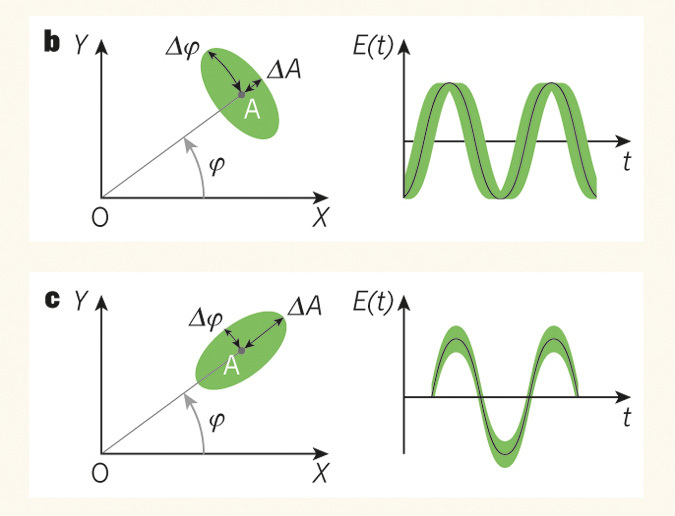
Такое состояние называется сжатым светом, потому что флуктуации амплитуды или фазы сжимаются вдоль одной из осей, уменьшая ошибку измерения. Первое называют амплитудным сжатием (эллипс вытянут поперек радиуса, можно точно померить амплитуду в максимумах-минимумах синусоиды); второе – фазовым (эллипс вдоль радиуса, можно померить фазу в нулях синусоиды).
Для обычного света мы не можем померить амплитуду или фазу точнее, чем нам дает кружок погрешностей. Это называется стандартным квантовым уровнем шумов. Сжатый свет позволяет уменьшить погрешность в одном направлении и «поднырнуть» под этот уровень шумов. В каком-то смысле мы можем [пафос_mode_on] делать более точные измерения, чем того хотела бы природа [пафос_mode_off].
Любой источник света каждую секунду генерирует целое число фотонов. Оно может меняться от секунды к секунде из-за квантовой природы света, образуя распределение числа фотонов (я упоминал это в рассказе про Хэнбери Брауна и Твисса).
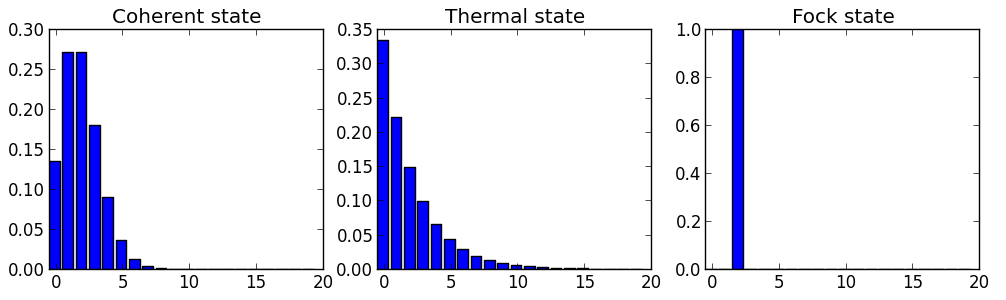
Число фотонов – это то же самое, что и интенсивность света. То есть интенсивность немного «шумит» — меняется от секунды к секунде. Это и есть стандартный квантовый уровень шума.
А вот если число фотонов не меняется от секунды к секунде (рисунок справа), то интенсивность строго постоянна и лишена какого-либо шума. Именно это будет светом, максимально сжатым по амплитуде. Поток фотонов при этом выглядит как-то так:

То есть фотоны испускаются строго периодично. Если периодичность нарушается, свет все равно остается до какой-то степени сжатым.
В отличие от других экзотических объектов, применение сжатого света оказались весьма перспективными.
Телеком. Передача информации при помощи модуляции сжатой переменной (амплитуды (АМ) или фазы (FM), более общий термин квадратуры) позволяет увеличить отношение сигнал/шум. Возможно построение усилителей, который добавляют шум только в ту квадратуру, которая несжата и не несет полезного сигнала.
Квантовая запутанность. В некоторых случаях можно проводить параллели между запутанностью фотонов и сжатием света. Например, можно запутать два пучка света: один сжатый по амплитуде, второй – по фазе.
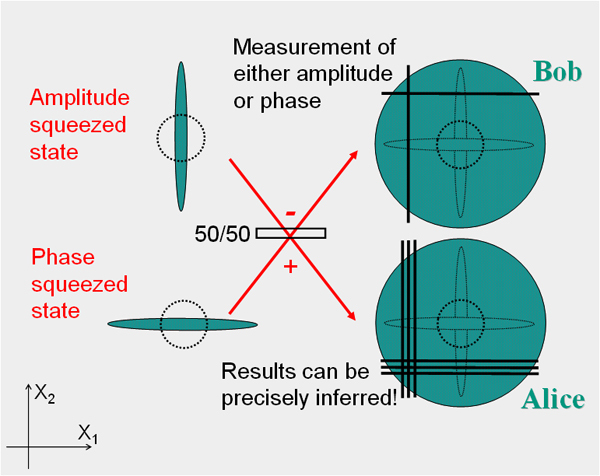
Квантовая криптография. Вытекает из квантовой запутанности и картинки выше. В простейшей схеме квантовой криптографии Алиса передает Бобу информацию при помощи фотонов со случайной поляризацией. Роль поляризации может играть направление сжатия: при неправильном его выборе злоумышленник, перехвативший канал связи, измерит не сигнал, а шум.
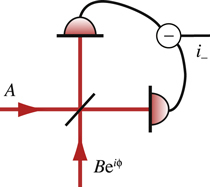
Детекторы гравитационных волн. Для этой задачи нужно улавливать мельчайшие колебания огромных грузов. Обычно это делается при помощи интерферометра Майкельсона. Он устроен очень просто: лазер, два зеркала и одна полупрозрачная пластинка:
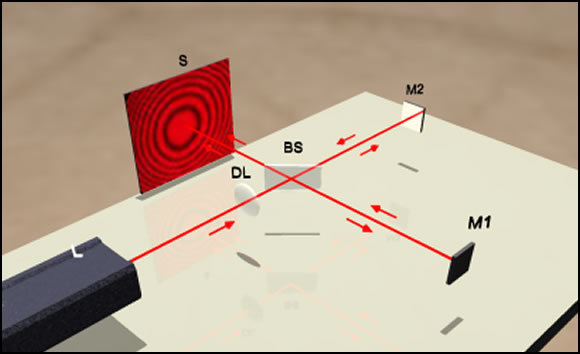
Лазер отражается от двух зеркал, два отражения интерферируют, и на экране образуется интерференционная картина. Если одно из зеркал движется, то движется и картина. Происходит это из-за изменения фазы волны: зеркало отодвинулось – путь лазера стал чуть дольше, набежала дополнительная фаза – интерференционные полоски сдвинулись.
Так как интерферометр измеряет фазу, его разрешение не может быть лучше, чем неопределенность фазы. Для обычного лазера она ограничена стандартным квантовым уровнем шума. А вот если заменить лазер на источник фазово-сжатого света, то эта проблема исчезнет, и мы сможем измерять расстояния с невиданной точностью.
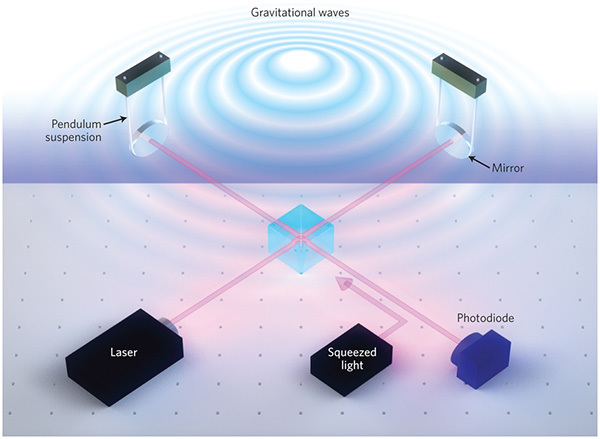
Сегодня это делается в одном из крупнейших детекторов гравитационных волн GEO600, и, по всей видимости, планируется на космическом детекторе LISA. Кстати, среди пользователей GT есть Shkaff, который как раз этим и занимается и готов ответить на ваши вопросы в комментариях. :)
Точное измерение фазы. Фазово-сжатый свет может быть полезен для измерений методом фазового контраста – повседневной методики в современной биологии.
Создать сжатый свет не так просто. Для этого применяют нелинейные оптические процессы. На пальцах их объяснить довольно сложно, но один пример приведу.
В некоторых кристаллах наблюдается эффект под названием нелинейность Керра – зависимость показателя преломления от интенсивности света. Пошлем на такой кристалл лазерный импульс. У любого импульса интенсивность на фронтах ниже, чем в центре – а значит, показатель преломления наиболее сильно изменятся там, где сейчас находится центр импульса. Разница показателей преломления приводит к тому, что фаза волны в центре и на фронтах меняется по-разному. Совокупность этих изменений приводит к тому, что фаза становится определена чуть лучше, чем обычно, а интенсивность – наоборот, чуть хуже. Здравствуй, сжатый свет :).
Измерить сжатый свет можно тоже несколькими способами.
1. Схема Хэнбери Брауна – Твисса.
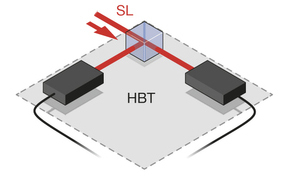
В цикле про Хэнбери Брауна и Твисса я рассказывал, что корреляционная функция g(2) соответствует ширине распределения числа фотонов. Амплитудное сжатие света означает, что число фотонов определено лучше, чем обычно. Поэтому в широком смысле слова g(2) меньше единицы – признак сжатого света.
2. Балансный детектор. Это как схема Хэнбери Брауна – Твисса, но вместо корреляций мы либо вычитаем, либо складываем сигналы с двух диодов (по нашему желанию):
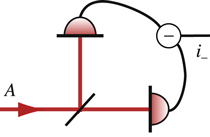
Полупрозрачное зеркало пропускает или отражает каждый фотон случайно. Эта случайность вносит в сигнал дополнительный квантовый шум (типа дробового). Такой шум имеет разный знак на двух диодах: если фотон отразился, то он не пролетит; если пролетел – не отразится.
Если мы вычтем сигнал одного диода из другого, то квантовый шум никуда не денется. А если сложим? Тогда шум пропадет, потому что он имеет разный знак. (Другое объяснение: мы разделили свет на две части, а потом сложили их обратно – дополнительного шума это, очевидно, не прибавило.)
Итак, вычитание добавляет нам шум со стандартным квантовым уровнем, а сложение ничего не меняет. Если изучаемый свет был амплитудно-сжатым (т.е. «бесшумным»), то вычитание сделает его более шумным, а сложение – оставит без изменений. Переключаясь между сложением и вычитанием, мы можем измерять уровень шума, и если он отличается, то мы наблюдаем амплитудно-сжатый свет.
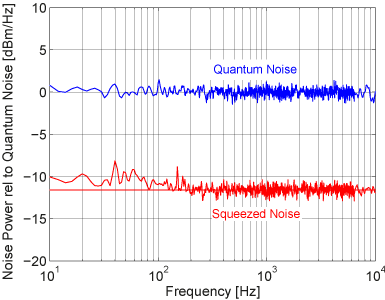
Примерно так выглядит шум после сложения (красный) и вычитания (синий). Красный шум гораздо слабее и соответствует сжатому свету.
3. Гомодинирование. Амплитудное сжатие измерить легко, а что же делать с фазовым? Если удастся «повернуть» ориентацию эллипса (то есть фазу света), то свет из сжатого по фазе станет сжатым по амплитуде. Фазу можно повернуть, смешивая свет с опорной волной. Это очень похоже на приемник-гетеродин, только в гетеродине частота опорной и изучаемой волн отличается, а в гомодине – нет (отсюда и название).
Еще в гомодине нужно подобрать фазу опорной волны. В электронике это делается фазовращателем, в оптике – линией задержки (чем позже придет свет, тем больше набежит фаза). Смешивание происходит на том же полупрозрачном зеркале:
Опорная волна подходит снизу. А дальше – тот же балансный детектор.
Пока что сжатый свет используется только в сверхточной интерферометрии. Проблема в том, что он оказывается невероятно хрупким. Это легко понять на примере идеального амплитудно-сжатого света (поток фотонов строго периодичен):

При распространении света неизбежны потери, которые всегда случайны. Это значит, что фотоны будут исчезать из потока случайным образом:

Как видно, от периодичности почти ничего не осталось. Равно как и от сжатия. Поэтому сжатый свет очень сложно передавать на большие расстояния.
Ну и напоследок давайте полюбуемся схемой гравитационного детектора GEO 600 под Ганновером:
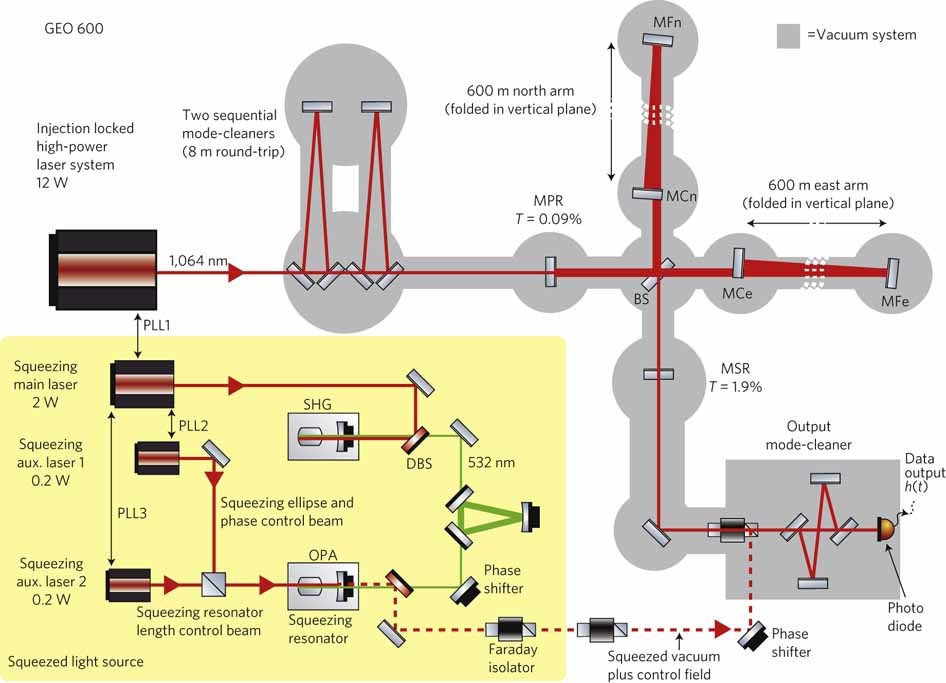
Источник сжатого света – на желтом фоне. В нем используется нелинейный оптический процесс, но не нелинейность Керра, а генерация второй гармоники излучения. Красный пунктир – это и есть сжатый свет. Сверху-справа – интерферометр Майкельсона с плечами по 600 метров; зеркала подвешены на грузах, которые должны колебаться от гравитационных волн. Картинка с интерферометра получается на фотодиоде в нижнем правом углу.
Источники
M. Fox. Quantum optics: An Introduction – Oxford University Press, 2006.
Спасибо Shkaff за экспертные комментарии.
Картинки: КДПВ, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

Полицейский останавливает Гейзенберга, превысившего скорость.(бородатый анекдот)
– Вы хоть знаете с какой скоростью вы ехали?
– Нет, но зато я точно знаю, где я находился.
Соотношение неопределенностей Гейзенберга запрещает одновременно измерить координату и скорость (импульс) частицы. При этом никто не мешает точно померить одну из величин – но тогда неопределенность второй станет еще больше.

Вообще соотношения неопределенностей встречаются в физике довольно часто. Например, такое же соотношение верно для электромагнитной волны: оно связывает ее интенсивность (= число фотонов) и фазу:

Из-за этой неопределенности мы не можем точно измерить описываемую волной синусоиду, для наблюдателя она всегда будет в шумовой дымке:

Это можно наглядно показать на круговой диаграмме, где амплитуде соответствует радиус до точки, фазе – угол между направлением на точку и осью Х. Зеленым показана неопределенность:

При этом никто не мешает точно определить либо амплитуду, либо фазу. Тогда кружок погрешностей превратится в эллипс, сжавшись в одном направлении и вытянувшись в другом:

Такое состояние называется сжатым светом, потому что флуктуации амплитуды или фазы сжимаются вдоль одной из осей, уменьшая ошибку измерения. Первое называют амплитудным сжатием (эллипс вытянут поперек радиуса, можно точно померить амплитуду в максимумах-минимумах синусоиды); второе – фазовым (эллипс вдоль радиуса, можно померить фазу в нулях синусоиды).
Почему это важно?
Для обычного света мы не можем померить амплитуду или фазу точнее, чем нам дает кружок погрешностей. Это называется стандартным квантовым уровнем шумов. Сжатый свет позволяет уменьшить погрешность в одном направлении и «поднырнуть» под этот уровень шумов. В каком-то смысле мы можем [пафос_mode_on] делать более точные измерения, чем того хотела бы природа [пафос_mode_off].
Простой пример.
Любой источник света каждую секунду генерирует целое число фотонов. Оно может меняться от секунды к секунде из-за квантовой природы света, образуя распределение числа фотонов (я упоминал это в рассказе про Хэнбери Брауна и Твисса).

Число фотонов – это то же самое, что и интенсивность света. То есть интенсивность немного «шумит» — меняется от секунды к секунде. Это и есть стандартный квантовый уровень шума.
А вот если число фотонов не меняется от секунды к секунде (рисунок справа), то интенсивность строго постоянна и лишена какого-либо шума. Именно это будет светом, максимально сжатым по амплитуде. Поток фотонов при этом выглядит как-то так:

То есть фотоны испускаются строго периодично. Если периодичность нарушается, свет все равно остается до какой-то степени сжатым.
Зачем это нужно?
В отличие от других экзотических объектов, применение сжатого света оказались весьма перспективными.
Телеком. Передача информации при помощи модуляции сжатой переменной (амплитуды (АМ) или фазы (FM), более общий термин квадратуры) позволяет увеличить отношение сигнал/шум. Возможно построение усилителей, который добавляют шум только в ту квадратуру, которая несжата и не несет полезного сигнала.
Квантовая запутанность. В некоторых случаях можно проводить параллели между запутанностью фотонов и сжатием света. Например, можно запутать два пучка света: один сжатый по амплитуде, второй – по фазе.

Квантовая криптография. Вытекает из квантовой запутанности и картинки выше. В простейшей схеме квантовой криптографии Алиса передает Бобу информацию при помощи фотонов со случайной поляризацией. Роль поляризации может играть направление сжатия: при неправильном его выборе злоумышленник, перехвативший канал связи, измерит не сигнал, а шум.
Детекторы гравитационных волн. Для этой задачи нужно улавливать мельчайшие колебания огромных грузов. Обычно это делается при помощи интерферометра Майкельсона. Он устроен очень просто: лазер, два зеркала и одна полупрозрачная пластинка:

Лазер отражается от двух зеркал, два отражения интерферируют, и на экране образуется интерференционная картина. Если одно из зеркал движется, то движется и картина. Происходит это из-за изменения фазы волны: зеркало отодвинулось – путь лазера стал чуть дольше, набежала дополнительная фаза – интерференционные полоски сдвинулись.
Так как интерферометр измеряет фазу, его разрешение не может быть лучше, чем неопределенность фазы. Для обычного лазера она ограничена стандартным квантовым уровнем шума. А вот если заменить лазер на источник фазово-сжатого света, то эта проблема исчезнет, и мы сможем измерять расстояния с невиданной точностью.

Сегодня это делается в одном из крупнейших детекторов гравитационных волн GEO600, и, по всей видимости, планируется на космическом детекторе LISA. Кстати, среди пользователей GT есть Shkaff, который как раз этим и занимается и готов ответить на ваши вопросы в комментариях. :)
Точное измерение фазы. Фазово-сжатый свет может быть полезен для измерений методом фазового контраста – повседневной методики в современной биологии.
Как сгенирировать?
Создать сжатый свет не так просто. Для этого применяют нелинейные оптические процессы. На пальцах их объяснить довольно сложно, но один пример приведу.
В некоторых кристаллах наблюдается эффект под названием нелинейность Керра – зависимость показателя преломления от интенсивности света. Пошлем на такой кристалл лазерный импульс. У любого импульса интенсивность на фронтах ниже, чем в центре – а значит, показатель преломления наиболее сильно изменятся там, где сейчас находится центр импульса. Разница показателей преломления приводит к тому, что фаза волны в центре и на фронтах меняется по-разному. Совокупность этих изменений приводит к тому, что фаза становится определена чуть лучше, чем обычно, а интенсивность – наоборот, чуть хуже. Здравствуй, сжатый свет :).
Как засечь?
Измерить сжатый свет можно тоже несколькими способами.
1. Схема Хэнбери Брауна – Твисса.

В цикле про Хэнбери Брауна и Твисса я рассказывал, что корреляционная функция g(2) соответствует ширине распределения числа фотонов. Амплитудное сжатие света означает, что число фотонов определено лучше, чем обычно. Поэтому в широком смысле слова g(2) меньше единицы – признак сжатого света.
2. Балансный детектор. Это как схема Хэнбери Брауна – Твисса, но вместо корреляций мы либо вычитаем, либо складываем сигналы с двух диодов (по нашему желанию):

Полупрозрачное зеркало пропускает или отражает каждый фотон случайно. Эта случайность вносит в сигнал дополнительный квантовый шум (типа дробового). Такой шум имеет разный знак на двух диодах: если фотон отразился, то он не пролетит; если пролетел – не отразится.
Если мы вычтем сигнал одного диода из другого, то квантовый шум никуда не денется. А если сложим? Тогда шум пропадет, потому что он имеет разный знак. (Другое объяснение: мы разделили свет на две части, а потом сложили их обратно – дополнительного шума это, очевидно, не прибавило.)
Итак, вычитание добавляет нам шум со стандартным квантовым уровнем, а сложение ничего не меняет. Если изучаемый свет был амплитудно-сжатым (т.е. «бесшумным»), то вычитание сделает его более шумным, а сложение – оставит без изменений. Переключаясь между сложением и вычитанием, мы можем измерять уровень шума, и если он отличается, то мы наблюдаем амплитудно-сжатый свет.

Примерно так выглядит шум после сложения (красный) и вычитания (синий). Красный шум гораздо слабее и соответствует сжатому свету.
3. Гомодинирование. Амплитудное сжатие измерить легко, а что же делать с фазовым? Если удастся «повернуть» ориентацию эллипса (то есть фазу света), то свет из сжатого по фазе станет сжатым по амплитуде. Фазу можно повернуть, смешивая свет с опорной волной. Это очень похоже на приемник-гетеродин, только в гетеродине частота опорной и изучаемой волн отличается, а в гомодине – нет (отсюда и название).
Еще в гомодине нужно подобрать фазу опорной волны. В электронике это делается фазовращателем, в оптике – линией задержки (чем позже придет свет, тем больше набежит фаза). Смешивание происходит на том же полупрозрачном зеркале:

Опорная волна подходит снизу. А дальше – тот же балансный детектор.
И еще из интересного
Пока что сжатый свет используется только в сверхточной интерферометрии. Проблема в том, что он оказывается невероятно хрупким. Это легко понять на примере идеального амплитудно-сжатого света (поток фотонов строго периодичен):

При распространении света неизбежны потери, которые всегда случайны. Это значит, что фотоны будут исчезать из потока случайным образом:

Как видно, от периодичности почти ничего не осталось. Равно как и от сжатия. Поэтому сжатый свет очень сложно передавать на большие расстояния.
Ну и напоследок давайте полюбуемся схемой гравитационного детектора GEO 600 под Ганновером:

Источник сжатого света – на желтом фоне. В нем используется нелинейный оптический процесс, но не нелинейность Керра, а генерация второй гармоники излучения. Красный пунктир – это и есть сжатый свет. Сверху-справа – интерферометр Майкельсона с плечами по 600 метров; зеркала подвешены на грузах, которые должны колебаться от гравитационных волн. Картинка с интерферометра получается на фотодиоде в нижнем правом углу.
Источники
M. Fox. Quantum optics: An Introduction – Oxford University Press, 2006.
Спасибо Shkaff за экспертные комментарии.
Картинки: КДПВ, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Комментарии (44)
zuborg
27.11.2015 21:19А что за обобщенная координата используется на графиках? Т.е. что конкретно меняется по синусоидальному закону? Явно ж не собственно интенсивность света.
qbertych
28.11.2015 00:07+1Время. Когда волна распространяется, в каждой точке пространства пучности волны периодически сменяются минимумами.
Но с тем же успехом можно использовать координату: если сделать «моментальный снимок волны сбоку», она будет казаться синусоидальной.


yatagarasu
а какое минимальное расстояние между фотонами?
Zenitchik
Никакое. Фотоны — это бозоны, они могут хоть друг на друга накладываться.
voyager-1
У фотонов нет такой «ненависти» к друг другу — на них не действует принцип запрещения Паули, так что ограничений в этом плане нет. Ну разве что вы умудритесь накачать в очень маленькую область столько фотонов, что чёрная дыра образуется). Но это — явно ещё за пределами наших возможностей.
yatagarasu
А сколько надо накачать? )
Meklon
Лучше не надо) обещайте, что не будете.
yatagarasu
Нет ну интересно же. Я же не усну пока не посчитаю.
А какой минимальный объём могут занимать несколько фотонов?
У фотона вообще объём есть?
Хотя тут полагаю надо сразу исходить из радиуса Чёрной Дыры, которую стоит цель получить.
DmitriyN
Вот тут почитайте о черных дырах из фотонов: https://en.wikipedia.org/wiki/Kugelblitz_(astrophysics). А объема у фотона нет :)
stalinets
Но ведь фотон-фотонное взаимодействие возможно и изучается.
qbertych
Фотоны напрямую друг с другом не взаимодействуют. Причина в линейности уравнений Максвелла (основных уравнений электродинамики): если мы пошлем в систему в два раза больше фотонов, то отклик будет ровно в два раза больше. Если бы фотоны взаимодействовали, отклик был бы другим (нелинейным).
Собственно, поэтому нелинейная оптика и называется нелинейной: ее задача — заставить фотоны взаимодействовать друг с другом. Это успешно делается, при этом не имея отношения к LHC, черным дырам и подобным чудесным вещам.
Greendq
Кстати, а это вообще возможно в теории? Если у фотонов нет массы — и их можно напихать сколько угодно в ограниченное пространство — то откуда ЧД появится?
Banzeg
Как это — нет массы у фотонов?
MaximChistov
у фотонов нет массы _покоя_
Greendq
Ну так я же не «спокойные» фотоны собираюсь подловить :)
MaximChistov
ну тут проблема в том, что фотоны летят исключительно прямолинейно. то есть чтобы собрать их нужное количество в одной точке, вам надо абсолютно одновременно все их выпустить из равноудаленных точек пространства. а еще это нарушит принцип неопределенности, ведь для этого вам нужно будет одновременно очень точно задать их положение в пространстве и скорость, что невозможно
voyager-1
Это (принцип неопределённости) накладывает ограничения на минимальную энергию фотонов, с помощью которых можно создать чёрную дыру (у неё будет нижний предел на размеры/массу), но не запрещает сам факт возможности её создания таким образом).
MaximChistov
Greendq, как я понял, говорил про ручное создание. Вот оно-то невозможно, насколько я понимаю.
Banzeg
что насчет гравитационных линз, уважаемый?
MaximChistov
Они искривляют пространство так, что с точки зрения стороннего наблюдателя траектория не прямая. А с точки зрения фотона его путь идеально прямой
Banzeg
Искривляют пространство как?
Что с точки зрения стороннего наблюдателя, находящегося в менее искривленном пространстве, наблюдающего за движением фотона в более искривленном пространстве, фотон движется по искривленной траектории, хотя на самом деле движется прямолинейно? А чем фотон отличается от любых других тел, таких, как мы с вами, но, в менее искривленном пространстве с точки зрения физики движения? Смею утверждать, что двигаюсь в каждый момент времени прямолинейно (и это не беря во внимание искривление пространства земной гравитацией).
Серьезно, объясните.
voyager-1
Речь видимо про то, что нам надо собрать огромную концентрацию фотонов в минимальный промежуток времени и места. Тут гравитационная линза может помочь лишь с концентрацией фотонов (как собственно и обычная линза), а расширить промежуток времени, за который их можно собирать — она не сможет (фотоны всё равно будут улетать до тех пор, пока ваша грав-линза не достигнет предела Шварцшильда).
По этой теме есть пара интересных умозаключений (физически их проверить пока не возможно, возможно проверить их не получится и вовсе никогда): существует Планковская масса — это предел для массы фотона, превысив который, он превратится в чёрную дыру (без дополнительной «помощи» в виде частиц рядом).
Частота этой частицы порождает Планковскую длину — предельно малую длину, которую можно измерить (ибо частиц, способных измерить меньшие длины просто не может существовать — они просто «схлопнутся» в чёрную дыру). Но само по себе это не доказывает квантовости пространства (наличие какой-то «сетки» пространства, по точкам которой можно только прыгать, но нельзя оказаться между ними).
vintage
С точки зрения пушечного ядра, его путь идеально прямой в этом не идеальном кривом пространстве. Но на мой взгляд контрпродуктивно считать ускорение в сторону минимума потенциала прямолинейным движением. Не, я понимаю, что если молиться на электромагнитные волны, то ничего другого не остаётся. Но можно ведь и более критически относиться к постулатам :-)
lavmax
Про фотоны кстати не очень этого понимаю. Если точно измерить положение фотона в пространстве, то все сломается? Ведь скорость фотона постоянна и в отдельном измерении не нуждается.
MaximChistov
постоянен только модуль скорости, а вот про его направление вам ничего не известно
Mingun
Но ведь на самом деле нужны три координаты:
1. номер фотона
2. положение фотона
3. скорость фотона
Нельзя ли это как-то использовать? Для каждого конкретного фотона мы не знаем ни точно скорость, ни точно положение, но для группы, это, вероятно, возможно. Ведь как-то удается делать эксперименты с термоядом, пуляя в одну точку несколько лазерных лучей с разных направлений и никакие принципы не нарушаются.
Shkaff
Позвольте-с, а откуда номер-то? Для каждого конкретного фотона ограничение исключительно на точность координаты и импульса (не скорости).
Mingun
Определение «конкретного» подразумевает, что их можно сосчитать (в противном случае вы не можете говорить о конкретном фотоне, а только о какой-то неопределенной «массе», «жиже» фотонов), а значит, присвоить номер.
Shkaff
Хорошо. Тогда, конечно, это называется ЭПР парадокс — для двух запутанных частиц (фотонов) можно точно знать сумму координат и разность импульсов, но это очень специальный пример. В общем случае для группы частиц действуют все те же правила — скажем, и координату и импульс центра масс знать точно нельзя (для фотонов — что-нибудь типа общего места точек будет).
qbertych
Еще рядом стоит обменное взаимодействие: сосчитать фотоны может быть и можно, но пронумеровать — нельзя, потому что они неотличимы.
Mingun
Не понимаю, почему нельзя нумеровать, если мы их можем сосчитать. Если нам нужно сохранять привязку одних и тех же номеров к фотонам, то это наверное и нельзя из-за их неотличимости, а если сохранять такое соответствие не нужно? Ведь и импульс, и скорость мы тоже будем мерить на конкретный момент времени. Правда, при таких условиях все эти измерения становится, похоже, бесполезными и ничего интересного из них не вытащить…
Shkaff
Это основополагающий принцип квантовой механики — принцип неразличимости тождественных частиц (неплохо написано в английской вики). По сути дела, если частицы тождественны, единственным методом их отличить друг от друга было бы «прилепить табличку» и следить, куда и как частица движется. Но в квантовой физике траектории частиц не определены и носят вероятностный характер, так что в итоге все траектории «перемешиваются» и становится невозможно сказать, где же частица, за которой вы следили.
Mingun
Вот именно что различать требуется, если нужно следить за частицей. А при измерении импульса и положения зачем следить за ее дальнейшей судьбой? Тут единственная проблема получается, что можно регистрировать несколько раз одну и ту же частицу
Другое дело, что обычно как раз дальнейшая судьба и интересна, поэтому я и написал выше, что такие измерения, если они возможны, вобщем-то бесполезны.
FransuaMaryDelone
Я пробовал как-то: насыпал две ложки сахару в чай, размешал, и начал эти ложки нумеровать — не получилось. На вкус всё точно — две ложки сахару в чае, а номеров у ложек — не видать.
doobrik
Фотон — безмассовая частица, при чём тут покоя или не покоя. Можно подумать, у _беспокойного_ фотона масса есть.
forgotten
Это неграмотное суждение. Специальная теория относительности оперировала массами «покоя» и «движения», однако уже в Общей теории относительности Эйнштейн от этой концепции отказался (в рамках ОТО если попытаться определить «массу движения» как меру взаимодействия, она окажется разной в зависимости от направления). В школьных учебниках она почему-то при этом прижилась, и продолжает использоваться совершенно безграмотно.
У фотона нет массы. Вообще. Никакой.
ufn.ru/ufn89/ufn89_7/Russian/r897f.pdf
FransuaMaryDelone
Мне Л.Б. Окунь показался Планковским «аксиоматиком»:
"… существует кроме метафизиков и позитивистов еще
третья группа работников над физической картиной мира.
Она характеризуется тем, что ее главный интерес направлен
не на связь с реальным или чувственным миром, но на внутреннюю замкнутость и логическое построение физической картины мира. Это — аксиоматики. И их деятельность полезна и необходима. Но..."
М. Планк. Картина мира современной физики // УФН. — 1929. — Т. 9. — С. 407—436. (стр. 411)
faiwer
deleted