Я хочу посвятить эту статью известной задаче в математике, относящейся к теории вероятности. Так же мы попытаемся решить эту задачу на JavaScript. Я сразу приступлю к условию задачи.

Условие задачи

На картинке видно три двери. За одной из них находится новый автомобиль, а за другими двумя находятся козлы. Чему равна вероятность что за случайно выбранной дверью находится машина? Я думаю что тут всем понятно, что вероятность равна 1/3, или 33.3%. Затем я, как ведущий, попрошу вас выбрать одну из них. Давайте представим что вы выбрали левую дверь.

Затем, я открываю дверь в которой нет автомобиля, и заново спрашиваю вас, вы уверены в своем выборе или хотите изменить его? (Уточню, что ведущий не преследует никаких моральных или материальных ценностей, он выполняет свою работу не смотря на то, выбрали вы правильную дверь или же нет, так что не ищите подвох в этом плане ). Логично, что при таком выборе, следует опираться на вероятность. Исходя из этого ответьте себе на вопрос, какой шанс выбрать правильную дверь, чтобы выиграть автомобиль?

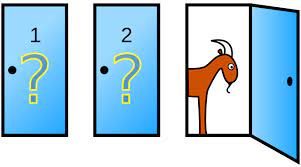
Вы ответили 50%? Это не верно.

Как бы это не казалось странным, шанс у двух дверей не одинаковый. Сначала разберем эту задачу с точки зрения человеческой логики, а потом с помощью JS.

Объяснение с помощью логики

Вернемся к начальной точке. Возьмем шанс одной двери и поставим его напротив шансов двух оставшихся, тут вопросов возникнуть не должно, понятно что левая дверь имеет шанс 1/3 (или 33.3%), а оставшиеся 2/3 (или 66.6%).

Теперь я уберу правую дверь, и покажу, что там ничего нет.

Но по картинке видно, что шанс правой двери просто перешел к средней двери, и теперь шанс что за ней автомобиль равен 2/3 (или 66.6%)!

Скорее всего это показалось не убедительным, и в голове возникают мысли о том что это просто актерский трюк, а котором явно есть подвох. Но это не так!

Какой лучший способ узнать шансы выпадения или получения чего либо? Конечно же это проделать эксперимент большое количество раз. В этом нам поможет JavaScript.

Решаем задачу неверным скриптом

Чтобы задача стала понятной до мелочей, сначала начнем с неправильного его решения с помощью JS, а потом перейдем к правильному, чтобы видеть что изменилось. Мы представим, что вы настойчивый игрок, и всегда будете оставлять свой выбор на двери, которую выбрали изначально. (В конце будет полный код чтобы вы могли его запустить у себя)

let lost = 0;
let won = 0;
const arr = [0, 1, 2];
let step = 0;

Тут все просто, на первых двух строчках объявлены переменные указывающие на количество выигрышей и проигрышей (то есть в каких случаях вы выбираете дверь с автомобилем, а в каких нет). На третей строчке - массив, числа в нем обозначают двери, и одновременно индексы элементов в нем. Четвертая строка это просто переменная для цикла while.

while (step < 100000) {
  //Последующий код будем писать внутри этого цикла
}

Я думаю что 100000 попыток будет вполне достаточно для того чтобы удостовериться в правильном ответе на задачу.

const secondArr = [...arr];

При каждой итерации цикла будет создавать массив, так так нам нужно будет на каждой итерации удалять из него элемент

Важно: скопировать массив обязательно нужно через оператор spread (...), так как если просто передать ссылку, родительский массив будет изменяться так же как и дочерний, и мы не получим корректного результата.
Можете вспомнить про оператор spread в документации по ссылке:

https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Operators/Spread_syntax

let removeIndex = Math.floor(Math.random() * secondArr.length);
secondArr.splice(removeIndex, 1);

Первую строчку выше пугаться не стоит, это просто вариант для взятия одного индекса (а соответственно и элемента, так так индексы и элементы в нашем массиве равны). А на второй строчке мы с помощью функция splice удаляем элемент с индексом который м ранее объявили,

Если вам нужно вспомнить что делает функция splice, советую обратиться к документации и освежить знания:

https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Array/splice

  let userIndex = Math.floor(Math.random() * secondArr.length);
  let wonIndex = Math.floor(Math.random() * secondArr.length);

Теперь объявим еще две случайные переменные, отвечающие за выбор пользователя, и за выигрышный выбор.

Дело за малым, сделать проверку, является ли выбор пользователя и выигрышный вариант равными

  if (wonIndex === userIndex) {
    won++;
  } else {
    lost++;
  }

Если да, прибавляем к выигрышам единицу, в противном случае к проигрышам.

  step++;

Ну и не забываем сказать что одна итерация завершена и прибавляем к step единицу.

console.log(won / 1000, lost / 1000);

Теперь снаружи цикла выводим результаты поделенные на 1000. Почему на тысячу? Хороший вопрос. Всего итераций 100000 (сто тысяч). Если бы мы разделили на 100000, то получили ответ в десятичной дроби (по типу 0.50), что не очень приятно для глаз, поэтому чтобы получить ответ в процентах, делим на 100 (1% = 0.01).

100000 / 100 = 1000

let lost = 0;
let won = 0;
const arr = [0, 1, 2];
let step = 0;
while (step < 100000) {
  const secondArr = [...arr];
  let removeIndex = Math.floor(Math.random() * secondArr.length);
  secondArr.splice(removeIndex, 1);
  let wonIndex = Math.floor(Math.random() * secondArr.length);
  let userIndex = Math.floor(Math.random() * secondArr.length);
  if (wonIndex === userIndex) {
    won++;
  } else {
    lost++;
  }
  step++;
}
console.log(won / 1000, lost / 1000);

Вот итоговый код который вы можете запустить и убедиться что при каждом запуске мы (в среднем) видим в консоли 50% выигрышей и проигрышей.

Почему первый скрипт не правильный

Очень хочется сказать что верхний скрипт полностью опровергает парадокс Монти Холла, но к сожалению это не так. Я специально допустил ошибку в этом скрипте, чтобы можно было провести сравнение между следующим.

А подвох начинается на 7-8 строчке, ведь мы просто берем случайный элемент и удаляем его из массива. И получается у нас в итоге просто массив с двумя элементами, и уже из него мы берем значения.

Это все равно что если бы я поставил перед вами только две двери и дал выбор. Поэтому мы и получаем такой ответ. В таком случае условие задачи не соответствуем тому что мы делаем в скрипте.

Решаем задачу правильным скриптом

let lost = 0;
let won = 0;
const arr = [0, 1, 2];
let step = 0;
while (step < 100000) {
  let secondArr = [...arr];
  let removeIndex; // <- Первое изменение здесь
  let wonIndex = Math.floor(Math.random() * secondArr.length);
  let userIndex = Math.floor(Math.random() * secondArr.length);
  // последующий код здесь
  /...
  }

Начало почти такое же, единственное мы просто объявляем переменную removeIndex. Но не присваиваем ей значение. А также не удаляем элемент из массива (пока что).

  for (let i of secondArr) {
    if (i !== userIndex && i !== wonIndex) {
      removeIndex = i;
    }
  }

Внутри while создаем еще один цикл, чтобы определиться какую дверь мы открываем, важно проверить, чтобы она не была равна выигрышной, а так же той, которую выбрал пользователь, так как в противном случае это не имеет никакого смысла.

  secondArr.splice(removeIndex, 1);
  if (wonIndex === userIndex) {
    won++;
  } else {
    lost++;
  }
  step++;
}
console.log(won / 1000, lost / 1000);

В конце цикла как и в прошлом скрипте просто удаляем элемент (в смысле открываем дверь) (но так как мы договорились что вы всегда стоите на своем, переменную userIndex можно не менять). А дальше опять простая проверка и вывод в консоль которые мы ранее разобрали.

И что вы думаете выведется в консоли? Как бы это не казалось бессмысленным, в консоли будет 33 и 66 (в среднем). То есть если вы будете стоять на своем и оставлять дверь которую выбрали изначально, вы выиграете лишь в 33% игр, а проиграете в 66%.

Вот весь скрипт:

let lost = 0;
let won = 0;
const arr = [0, 1, 2];
let step = 0;
while (step < 100000) {
  let secondArr = [...arr];
  let userIndex = Math.floor(Math.random() * secondArr.length);
  let wonIndex = Math.floor(Math.random() * secondArr.length);
  let removeIndex;
  for (let i of secondArr) {
    if (i !== userIndex && i !== wonIndex) {
      removeIndex = i;
    }
  }
  secondArr.splice(removeIndex, 1);
  if (wonIndex === userIndex) {
    won++;
  } else {
    lost++;
  }
  step++;
}
console.log(won / 1000, lost / 1000);

Итог

Если вы пройдетесь глазами по последнему скрипту, вы увидите что он практически полностью соответствуют условию задачи, и последовательность сохраняется.

Я уверен, что и это многих не убедило. Над этой задачей нужно хорошо подумать, чтобы полностью понять.

Несмотря на то что те кто первый слышит о данном парадоксе считает его ложным, и ищет в нем подвох, математики полностью его подтверждают, и основываются на нем как на факте, используя его для решения других, более сложных задач.

Надеюсь статья была полезной, и вы что то поняли, или начинаете понимать.