Предисловие

В 2020, когда случился локдаун, и к большому сожалению, появилось очень много свободного времени, мне захотелось познакомиться с Python. Начальный опыт c Pascal был еще со школы и универа, поэтому оставалось лишь придумать задачу и пойти её самоотверженно решать на питоне. Интересной задачей показалось смастерить игру змейку, прикрутить к ней мозги в виде перцептрона с парой скрытых слоёв, и путем кнута и яблока обучить цифровое животное выживать в жестоких реалиях двумерного мира.

«У самурая нет цели, есть только путь»

Первый блин на производстве не отличается красотой, но опыт был получен. Наиболее привлекательным мне пришелся генетический алгоритм: отбор успешных змеек, скрещивание, частичная мутация генов и так тысячи раз до результата. Змейки, без указания им правил выживания, в тысячном поколении «понимали», что нужно стремиться съесть яблоко и никуда не врезаться, это вызывало ощущение прикосновения к чуду "It's Alive!!!"

Спустя пару лет, закончив курс по аналитике данных, появилось желание переписать проект, попрактиковаться в более серьезных разделах python и сделать тренажёр со сбором статистики.

Итак, теперь были обозначены цели нового проекта:

1. Построить модель игры змейка, используя подходы ООП

2. Распараллелить на потоки некоторые вычисления (аппетит приходит во время еды, очень хотелось загрузить ядра процессора по максимуму, сократить время расчета)

3. Создать информативную оболочку с анимацией и выводом прогресса отбора и обучения

4. Собрать и проанализировать статистику

5. Если повезет, выделить закономерности и сделать интересные выводы

Видео-спойлер полученного результата:

На этом этапе должен предупредить, статью нельзя воспринимать как некое обучающее пособие с подробным раскрытием материала по теме нейросетей или же как авторитетное мнение по генетическим алгоритмам. Я постараюсь описать свой путь создания приложения, показать результаты и поделиться философскими рассуждениями на тему. Но, если мой отчет по проделанной работе вызовет желание разобраться в теме эксперимента, поможет избежать ошибок или же натолкнет читателя на какую-то свежую мысль – буду считать свою задачу перевыполненной. Во многом, я так закрываю свой гештальт 2020 года.

Статью разделю на 3 смысловые блока:

• описание модели

• логика процесса обучения и мои краткие выводы

• решения по коду тренажёра

---

Модель игрового мира змейки

Квадратное поле, по периметру стены, змейка на старте имеет одну клетку – голову и одну клетку – хвост, на любом свободном поле появляется яблоко.

Столкновение головы змейки со стеной или хвостом – смерть; количество ходов, превышающее пороговое значение, до съедания очередного яблока – голодная смерть.  За пороговое значение возьмём количество клеток игрового поля. Длинным змейкам нужен шанс обходить препятствие в виде своего же хвоста, при этом не уходить в бесконечные циклы перемещения.

Змейка может делать шаг в 4х направлениях, при этом, путь назад заведомо обречен – она натыкается на свой же хвост.

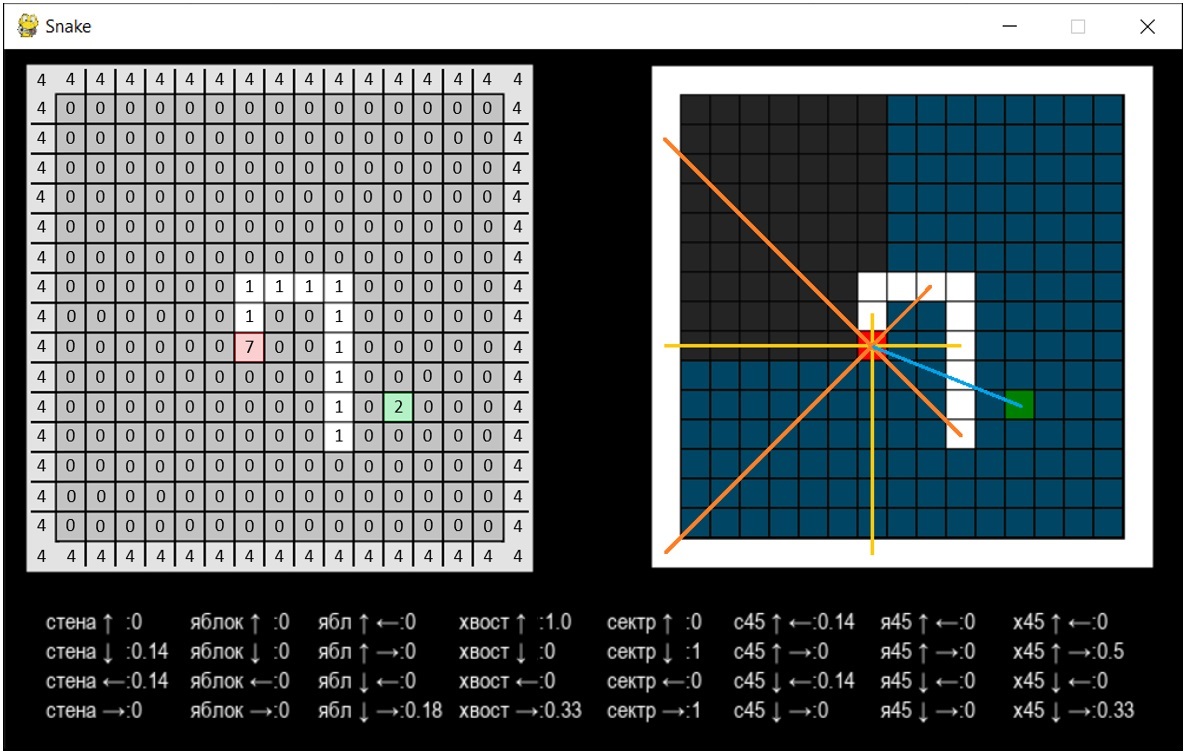
Цифровой эквивалент мира змейки – матрица, в которой каждая ячейка имеет свой маркер – цифру: пустая клетка = 0, стены = 4, тело = 1, голова = 7, еда = 2.
Такой подход существенно упрощает расчет для слоя сенсоров и позволяет отрисовать игровое поле, подавая в функцию графики матрицу целиком.

Информация о теле змеи хранится в виде списка координат: голова сделала ход на пустую клетку – добавили в список координаты нового положения головы в начало списка, последний элемент - удалили. Если было съедено яблоко – последний элемент хвоста не удаляется, таким образом наращивая длину змеи.

Сенсоры змейки

Змейка видит все, что есть в поле её зрения по вертикальным, горизонтальным и диагональным направлениям и имеет навигатор, который дает информацию о расположении яблока. С точки зрения алгоритма расчета, змейка не видит, а выпускает лучи из готовы и получает информацию о расстоянии до объектов (да, прабабушкой у неё была летучая мышь :)

Змейка в каждый момент знает:

• расстояние по вертикали и горизонтали от головы до первого объекта в поле зрения: стены, яблока или хвоста – 3 х 4 шт.

• аналогично по диагоналям – 3 х 4 шт.

• сектор, где находится яблоко, относительно головы: ниже/выше/слева/справа - 4 шт. (значения 0/1)

• кратчайшее расстояние от головы до яблока и направление до него (расчет гипотенузы) - 4 шт. а дальше пусть сама решает: катет не катит )

Расчет значений сенсоров решается простым циклом по координатам матрицы, от головы до первого встретившегося элемента не равному 0. Зная координаты головы и яблока, считаем гипотенузу, сектор яблока определяем путем сравнения координат по осям.

Если на пути луча встретился хвост, то в значение сенсора яблока и стен в этом направлении будет «0», она не увидит искомые объекты за препятствием. Некоторые данные нормализовал: близкий объект – 1, далекий – значение сенсора стремится к 0.

Размер поля. Как показала практика, обучить змейку бегать по полю и есть яблоки – дело несложное, получить за несколько минут работы алгоритма тех, кто ест 30-40 яблок за игру достаточно просто. Основной вопрос в том, что с каждым яблоком растет хвост и появляются проблемы маневрирования и поиска оптимальной модели поведения.

Больше размер поля – больше математических расчетов, время отбора увеличивается существенно. А цель поставлена амбициозная – вывести идеальную. Цель – съесть все яблоки, полностью заполнить хвостом игровое поле. Принял решение играть на поле 15 х 15 клеток. Максимальное количество яблок/очков – 223.

Нейросеть

Перед каждым ходом, змейка получает данные сенсоров, отправляет их на входящий слой нейросети и получает ответ, в какую сторону ей ползти.

Принимать решение о следующем ходе змейки будет перцептрон: 32 значения для первого слоя датчиков, 2 скрытых слоя и выходной слой – 4 направления движения. Размеры скрытых слоёв будем определять эмпирически. Размеры скрытых слоёв легко изменить перед каждым запуском симуляции в 2х соответствующих переменных.

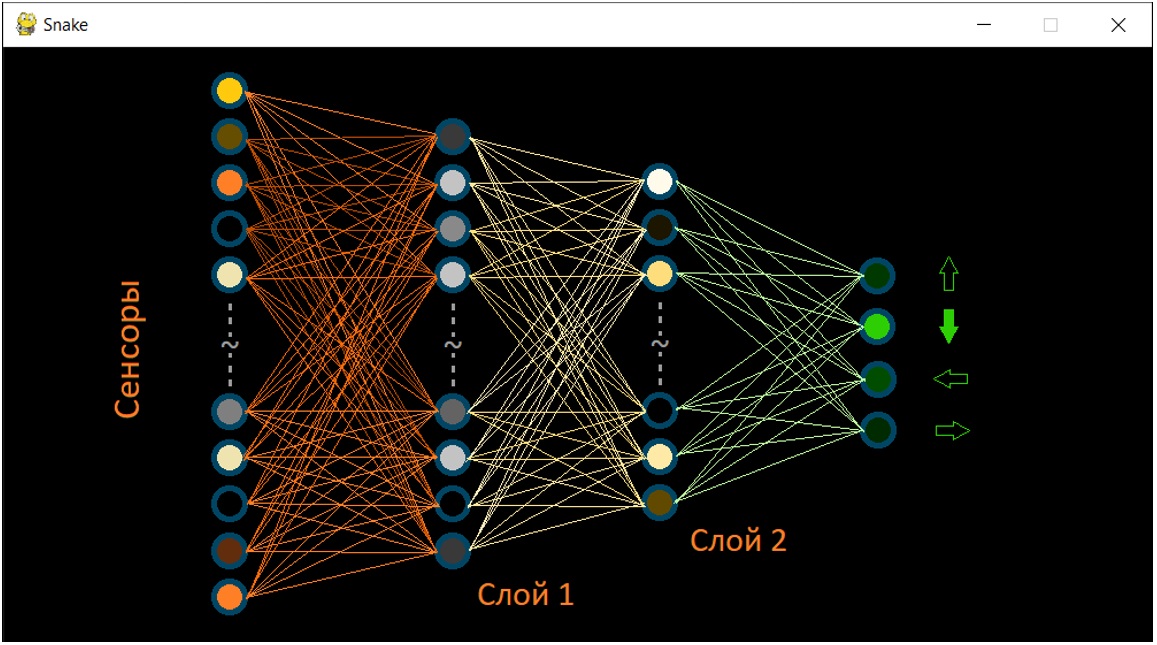
В этой части проекта можно было воспользоваться одной их стандартных библиотек, например, TensorFlow. Полагаю, это дало бы более простой в реализации и быстрый по расчету код, но… Обратный инжиниринг дедушкиного радиоприёмника для маленького физика – путь в угол, а для взрослеющего программиста – обучение! Поэтому никаких ML библиотек, только NumPy и скалярное умножение матриц, только хардкор! :)

Экспериментировал с разным количеством нейронов скрытых слоёв. Модель 32 х 12 х 8 х 4 показала значимый результат, функция активации ReLu. Увеличение количества связей между нейронами – синапсами приводит к росту времени расчетов на каждом ходе змеи. С другой стороны, большее количество нейронов скрытого слоя, скорее всего придаёт более сложное, «продуманное» поведение змейки в той или иной ситуации. Нужно искать баланс.

Файлы статистики и весов

После каждой игры, статистика сохраняется в файл *.csv для графиков и последующего анализа данных.

Данные в порядке записи: формат симуляции, номер семьи, эпоха, набранные очки, количество ходов, размер поля, количество сенсоров, размер слоя 1, размер слоя 2, количество лучших змей в отборе, количество змей в нулевой популяции, метка симуляции.

В отдельный файл *.bin сохраняются матрицы весов и результаты игр ТОП змей c данными: номер семьи, эпоха, список весов, список набранных очков, список количества ходов.  

---

Методы обучения и селекции

Изначально я видел 2 пути достижения цели:

1.      Обучать нейросеть для конкретной змейки через метод обратного распространения ошибки backpropagation. Для этого необходимо определить действия, за которые змейка получает поощрение и те, за которые получает наказание.
Генерируем случайные веса нейросети змейки и пускаем её в Мир. В зависимости от её действия корректируются значения тех весов между нейронами, которые привели к благоприятному или неблагоприятному исходу. Натаскиваем на нужное нам поведение. Пошла в сторону яблока – хорошо, съела яблоко – отлично, врезалась в стену или в хвост – плохо. Хорошо и отлично могут иметь разные корректирующие коэффициенты весов.

 2.      Генетический алгоритм. Генерируем нулевую популяцию – большое количество змеек (10 000 - 100 000) со случайными весами и отбираем лучших для скрещивания – тех, кто съел больше яблок за свою жизнь + иногда добавляем мутации, снова в игру... и так требуемого до результата.

По сути, каждая змея имеет свой набор генов – значения матриц весов между слоями сенсоров и нейронами слоев. Матрицы весов – набор числовых данных, диапазон значений от -1 до +1.

Поскольку мы собираем данные обо всех успешных змеях, сохраняем их веса, ничего не мешает нам их визуализировать и посмотреть, как же выглядят мозги змеи.
Матрицы между слоями можно представить в виде одномерного массива. Когда я увидел их диаграммы, сразу возникла ассоциация с тем, как изображают ДНК на картинках в умных книгах:

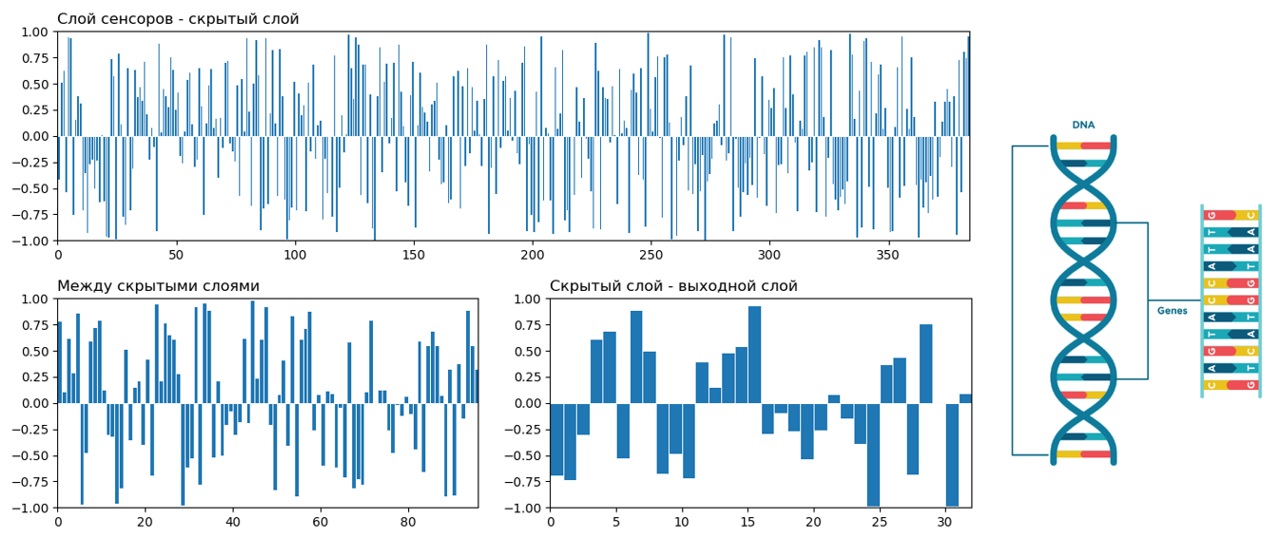
На диаграммах: по вертикали – значение веса связи между нейронами слоёв, по горизонтали номер связи. Для нейросети 32 х 12 х 8 х 4, количество связей первого и второго слоя: 32 х 12 = 384, для выходного 8х4 = 32.

Перемешивание генов успешных родителей, с последующим отбором лучших и есть путь к эволюции. Помимо скрещивания, у нового поколения могут добавляться мутации – непредсказуемое изменение малого количества генов 1% - 5%.

В первом проекте я тестировал оба метода, но больше проникся генетикой, это ближе к концепции Дарвинизма. Классическое обучение нейросети, я бы назвал контролируемой мутацией, но цель едина – изменить гены популяции для корректировки поведения. В текущем проекте будет только скрещивание и мутация.

Эпохи – количество поколений, оно же количество скрещиваний наиболее успешных родителей. Максимальным значением количества эпох до контроля результата принял 100.

Семьи – популяции отобранных (лучших со случайными весами) змеек, которые эволюционируют внутри своей группы. Для ускорения просчета можно параллельно формировать несколько семей и оценивать результат эволюции семейств за выбранное количество эпох.

Алгоритм селекции

1. Формируем нулевую популяцию змеек со случайными весами для каждой семьи

2. Отбираем ТОП показавших максимальные результаты

3. Скрещиваем ТОП + добавляем мутации

4. Повторяем с п.2 до 100й итерации

Для первого отбора из нулевой популяции я брал для скрещивания в 3 раза больше ТОП змеек – 45 шт., на последующих этапах отбиралось ТОП-15.

 Скрещивание происходило по следующей схеме:

• каждая с каждой с вероятностью взять ген одного из родителей 70% / 30%

• тот же принцип + мутация с вероятностью 5%

• полностью идентичные копии ТОП родителей

В итоге, для ТОП-15 новая популяция имеет размер: 15х15х2 + 15 =  465 змеек, для ТОП-45 – уже 4095.

Почему 70/30? – предположил, что «сильный ген» одного из родителей будет меньше давать сбой поведения при неудачном скрещивании, но большой разницы со схемой 50/50 в динамике результатов не заметил.

Экспериментируя с размерами нулевой популяции, за 100 эпох я регулярно видел достаточно уверенный рост результата, который к определенному моменту выходил на «плато».

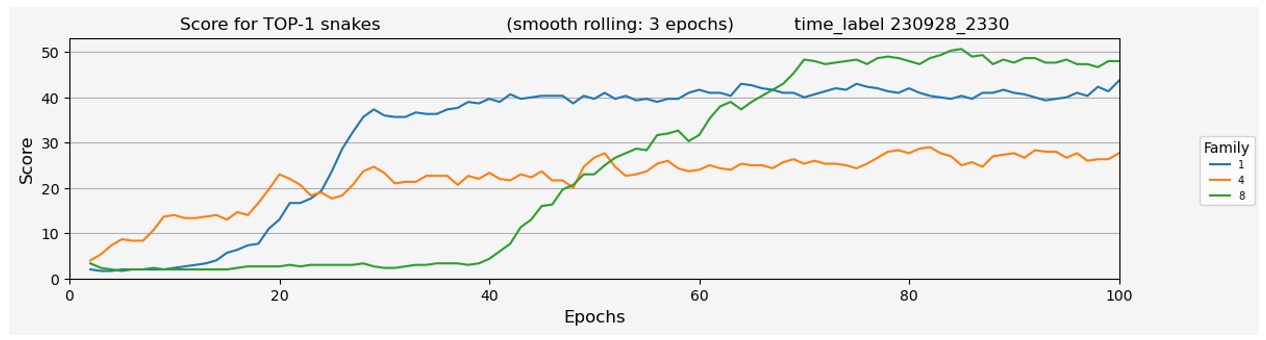
После стабилизации результатов семьи, редко возникал переход на более высокое плато. Вероятно, если это и происходило, то только за счет удачной мутации.

Возникла гипотеза, которую я захотел проверить.

Если взять 10 семей, вывести их на плато максимального результата и скрестить лидеров всех семейств, получим ли новую "взрывную" динамику развития у супер-семьи?

Создаем новый мир на 10 семей по 100 000 случайно сгенерировавшихся змеек, 100 эпох для каждой семьи.
Ну что, идеальная змейка: «Если ты смелый, ловкий умелый, Джунгли ЗОВУУУТ!!!»

Пара часов ожидания и результат радовал…. Я смотрел на график и чувствовался легкий привкус революционного открытия. Вспоминались слова отца: “Тима, заканчивай заниматься всякой... надо идти в аспирантуру и писать диссер!"

Но... потом я всё-таки нашел ошибку в коде своего алгоритма скрещивания :)))

Гипотеза оказалась ошибочной и вот почему.

Построив диаграммы генотипов лидеров семейств 100й эпохи, они оказались совершенно разными. Это можно увидеть даже по весам только выходных слоёв.

Значит все лидеры семейств реагировали на данные сенсоров по-своему и имели различные стратегии поведения.

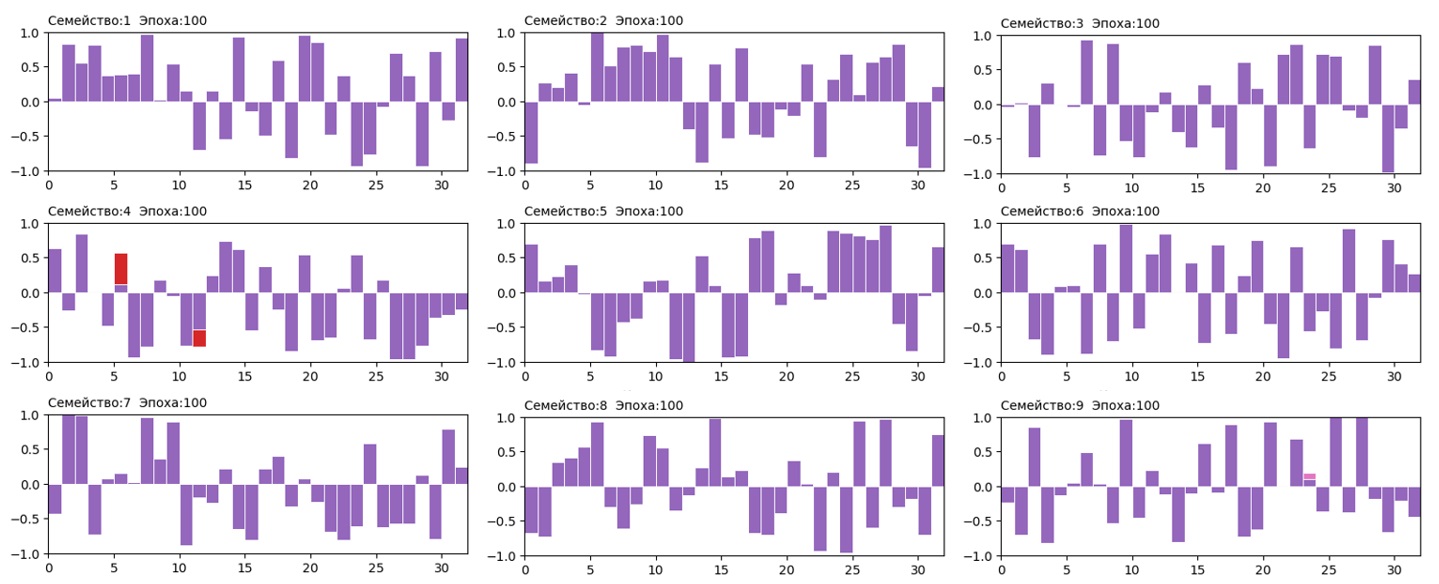
Полученные диаграммы – это наложение весов ТОП-15 для 100й эпохи каждой семьи, одинаковый цвет – полное совпадение генов. Можно заметить, что среди лидеров в семействе №4 есть один представитель с мутацией, показавший отличный результат в 100й эпохе. Какие-то синапсы с мутацией выделились на фоне большинства и подсветились красным.

Изменение весов внутри семьи от нулевой популяции до 100й эпохи в динамике выглядит так (обучение семейства №1 от 0 до 100 эпохи) :

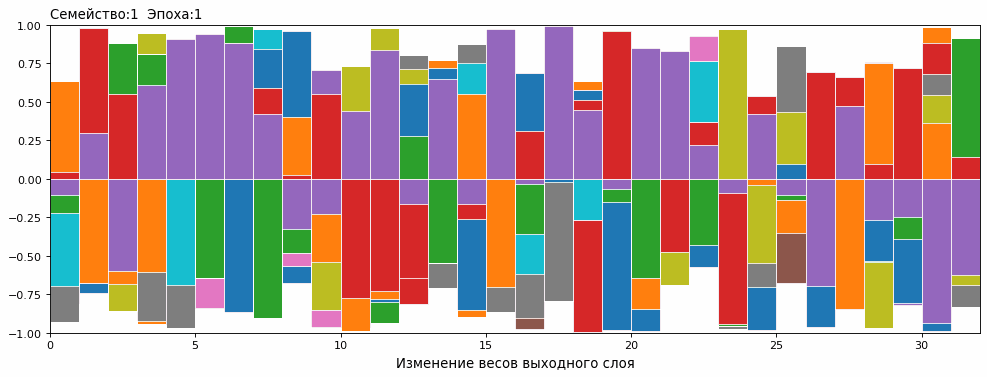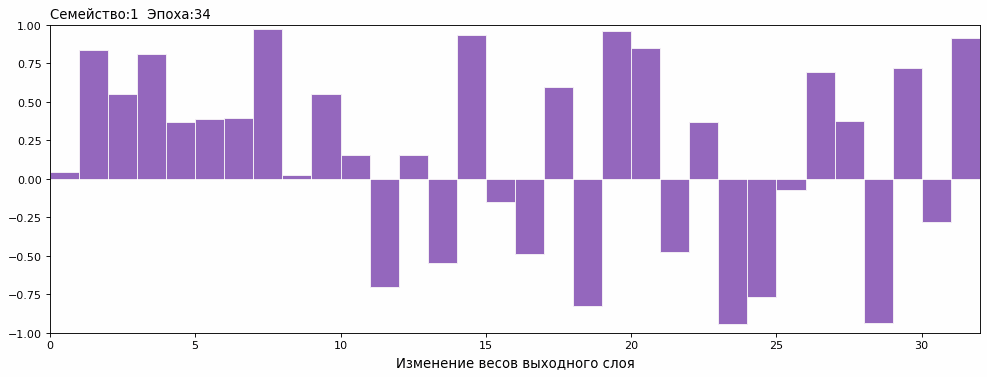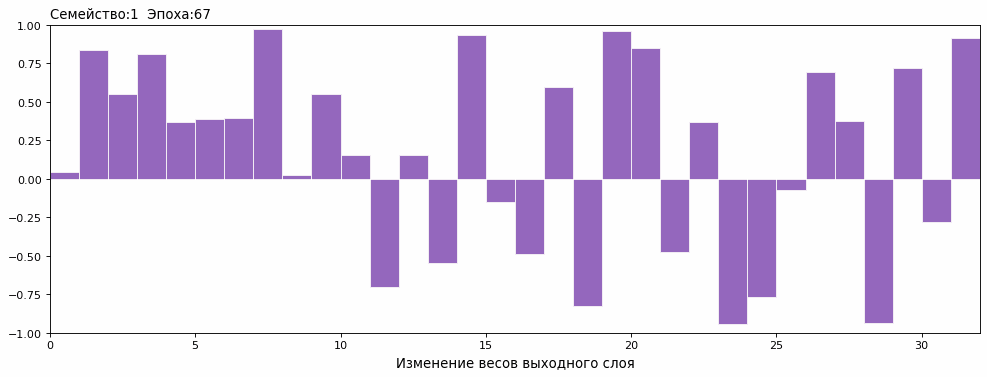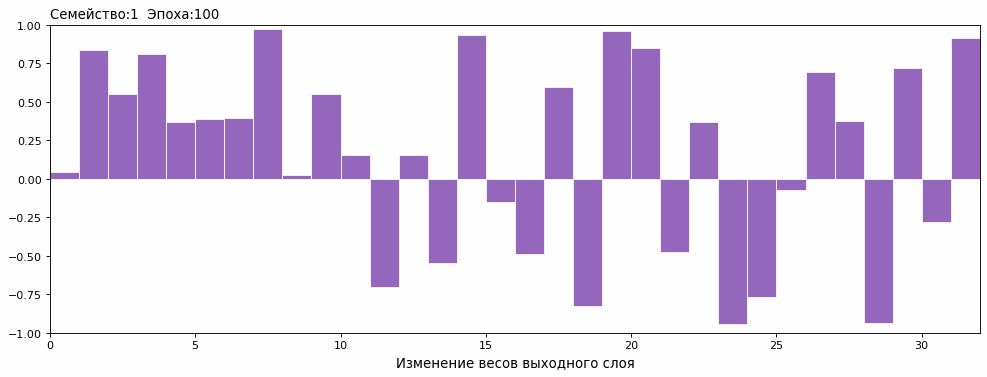
Сопоставив с графиком результатов, понял причину возникновения плато. Змеи в одном семействе, в определенный момент, стали одинаковыми.

На первом же этапе скрещивания в супер-семью, лидерство захватывают представители сильнейшего семейства и профиль генов выравнивается по генотипу лидера. На первом рисунке ниже – профиль популяции после скрещивания лидеров (полный винегрет) до игры, второй – отобранных ТОП лидеров после их игр, а третий рисунок – профиль лидеров из сильнейшей семьи до скрещивания.

Предполагаю, что на этапе, когда змеи делают первые шаги и совершают первые грубые ошибки, генотип потомков в конкретной популяции формируется за счет удачных фрагментов генотипа предка. Одна змея научилась не врезаться в левую стену и прожила дольше собратьев – передала часть навыков; вторая поняла, что нужно идти по направлению к яблоку – передала часть гена в общий котел. Понимая динамику роста результатов и зная процент мутации, мне кажется, что на этом этапе мутация практически не оказывает влияние на результат. Но это не точно :)

Путь селекции из одной популяции прародителей формирует определенный паттерн поведения всех последующих потомков. Это легко заметить, наблюдая за играми лучших из разных семейств. Прародители научились есть яблоко слева, делая ритуальный круг по часовой стрелке перед поеданием и это был лучший результат – все последующие поколения живут по канонам. Нашёлся мутировавший умник, у которого получилось съесть больше яблок за жизнь – он передаст детям новые подходы, а там эволюция решит, чьи потомки круче.

Значит путь к идеалу для супер-семьи лежит только через мутации!?

Детство, отрочество, юность

У каждой идеальной змейки есть несколько глобальных этапов развития, каждый со своими особенностями:

• куда ползти, чтобы съесть яблоко и не врезаться в стены

• как обходить препятствие из своего хвоста

• как укладывать хвост, чтобы оставлять зазор между стеной и хвостом и не попадать в западню 

Одна из симуляций дала максимальный результат змейки в 214 очков из 223 возможных. 216 заполненных клеток из 225 или 96% поля. Симуляция длилась более 27 часов (на Ryzen 7 5800U). 

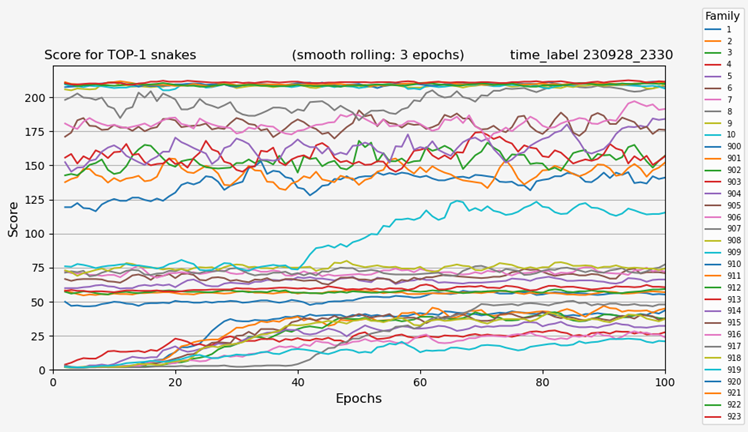
Результаты до 50 очков я бы отнес к первому этапу – найти и съесть.

До 80 очков – они учились обходить хвост, потом произошла мутация, которая дала резкий скачок в развитии.

На финальном этапе лидеры в среднем набирали 210 очков.

На 28 часу работы без динамики развития я уже четко улавливал мысли змейки: «Мне этот мир абсолютно понятен, и я здесь ищу только одного - покоя, умиротворения и вот этой гармонии, от слияния с бесконечно вечным.... понимаешь?»

Эксперимент был остановлен, максимальный результат в 214 яблок зафиксирован.

Резюмируя философскую часть статьи, мои выводы:

• Вся симуляция – игра с вероятностью во многом: начальные веса задают паттерн поведения лидеров 100й эпохи, дальше на динамику роста влияет мутация.

• Скрещивание дает быстрый результат только до формирования генотипа и выхода на плато результатов.

• Скрещивание сильных, но при этом разных по генотипу и, соответственно, по поведению змей не даёт резкого роста результата.

• С определенного момента основную роль играет мутация.

• Далеко не каждый расчет приведет к 100% результату в рамках адекватного временного ресурса.
  

---

Программа – тренажёр
https://github.com/tgladkiy/Snake

Применял стандартные и широко известные библиотеки:
os, time, datetime, pickle, shutil – размещения окна, время, дата и работа с файлами
(сохранение весов, статистики, графиков, копирование)
pygame – окно игры, анимация, вывод таблиц результатов
pandas, matplotlib – работа с данными, построение графиков обучения
multiprocessing – создание нескольких потоков для расчета случайных весов на несколько
семей одновременно
subprocess – создает процесс, открывая скрипт построения графика, сохраняет график в
файл

Написал модули для тренажёра:
В каждом модуле создается объект класса, который в своих атрибутах содержит информацию о состоянии, имеет функции изменения состояния, функции просчета.

snake_matrix.py  – поле и змейка. Формирует матрицу игрового поля, генерирует яблоки, хранит информацию о состоянии и текущем положении змейки, рассчитывает данные сенсоров
.new() – обновляет матрицу, создает новую игру
.sensors() – опрашивает сенсоры, возвращает список данных сенсоров
.move( [0,0,1,0] ) – получает команду на следующий ход, возвращает состояние жизни
змейки после хода: жива - True, погибла - False 

rnd_snakes.py  - генерация нулевых популяций и отбор лучших. При создании получает все параметры игры и требования по количеству семей и популяций.
.give_me_random_snakes() генерирует необходимое количество семей, змей для каждой
семьи, проводит первичный отбор лучших и возвращает словарь списков.
Ключи словаря - номер семейства
В списках словаря для каждого ключа хранит данные статистики отбора и данные о весах отобранных змей.

snake_ai.py – нейросеть, предсказание следующего хода. При создании получает параметры нейросети.
.get_w( w_in, w_lay, w_out ) – получает веса, записывает в атрибуты
.calculation( .sensors()  ) – получает список данных сенсоров, проводит расчет и
записывает в атрибут решение
.solution()  - возвращает список с предсказанием следующего хода [0, 0, 1, 0] - [↑,↓,←,→]
.w_suffle() и w_suffle_superfam () – получают три аргумента: список весов, % генов Родителя 1, % генов Родителя 2, % мутации. Первая функция для алгоритма скрещивания на этапе семейств, вторая – на этапе создания и скрещивания супер-семьи. Возвращают список весов потомства.

snake_draw.py - наполнение окна игры, отрисовки графики и таблиц
.param_table() – получает параметры игры и нейросети
.draw() – получает данные об окне и матрицу состояния игрового поля для анимации
.pivot_score() – отображение таблицы результатов по эпохам
.now_top() – отображение таблицы ТОП результатов текущей эпохи
.top_table() – отображение таблицы ТОП результатов за все игры
.draw_status() – отображение строки статуса, информация о горячих клавишах
.show_plot() – отображение графика 

plot_to_img.py  - скрипт открывается в отдельном процессе, берет данные из сохраненного файла статистики, генерирует график результатов семейств по эпохам, сохраняет график в файл.

Класс Sesion_snake() основного модуля хранит данные статистики игр, его функции фильтруют и сортирует данные змеек лидеров, сохраняют результаты в файлы.

Муки выбора, грабли и костыли

Графика

За графическую составляющую проекта была призвана отвечать библиотека PyGame.
Из плюсов: умеет рисовать простейшие фигуры, обновлять только нужные части экрана, обрабатывать нажатия клавиш и, ходят слухи, относительно шустрая.
Из минусов: отображает текст как картинки, а это усложняет задачу вывода таблиц на экран и, как выяснилось в процессе, конфликтует с библиотекой Matplotlib. Столкнуться с последним было крайне обидно, но в итоге помогло разобраться в том, как запускать сторонний скрипт из тела основной программы через модуль Subprocess.

Проблема: если импортировать и начать использовать PyGame и Matplotlib одновременно, в рамках одного скрипта, после запуска последнего окно приложения сжималось. Вычитал на stackoverflow, что при смешивании разные фреймворков, поведение всегда не определено и зависит от операционной системы. Некрасиво, неприятно, но не сдался.

Решение: создать отдельный скрипт plot_to_img.py, запускать его с параметром - названием метки игры (она определяет уже сохраненный на диске файл статистики). Внутри отдельно запущенного скрипта обрабатываются результаты, строится график и сохраняется в виде файла *.png.

Основной модуль не видит Matplotlib, загружает картинку и размещает в нужной части окна.
subprocess.call ( ['python.exe',  'plot_to_img.py' , str(time_label) ] )

После формирования нулевых популяций, тренажёр проводит игры змеек, анимация выключена, так как её отрисовка использует значительную часть ресурсов системы.

Можно управлять анимацией следующим образом:

• включение анимации – “о”

• выключение анимации – “p”

• увеличить скорость анимации – “f”

• уменьшить скорость анимации – “s”

• закрыть окно игры и остановить программу – “q”

Параллельные вычисления, многопоточность

Я заметил, что при расчете нулевой популяции большого размера, загружается только один поток процессора и это занимало достаточно много времени. А мне нужно считать 10 семей по 100 000 змеек, и это только до первой эпохи. Это не серьезно! Как загрузить ядра по максимуму?

Я нашел выход в использовании модуля multiprocessing.

Не скажу, что стал специалистом – это далеко не так, но решение своей скромной задачи нашел.

В моем подходе было важно распараллелить те вычисления, которые не будут влиять друг на друга и на ход выполнения общего скрипта. Как я понимаю, возможно и более сложное применение, но там сложная архитектура на уровне взаимодействия процессов – это уже ближе к высшему пилотажу, потренируемся пока на кошках змейках.

Проблемой было и понять, как передавать результат выполнения разных процессов, собирал информацию с разных веток обсуждения. В итоге разобрался, что можно формировать словарь, где ключи – номера процессов, данные словаря – все что получили в ходе расчетов.

Получилось ускориться в разы, практически кратно количеству запущенных процессов.
Одним словом – классная тема! Для нейросети 32х12х8х4, отбор лидеров из 500 000 случайных на 10 семей у меня занял 14 минут.

Если бы это было в 10 раз больше по времени… «Вкалывают роботы, счастлив человек!»

Приведу простой пример использования multiprocessing, возможно, кто-то ищет решение. Генерируется 7 потоков для расчета квадрата случайного числа, результат возвращается в виде словаря:

import multiprocessing as mp
import numpy as np

def random_x2(n_potok, return_dict):
    x = np.random.randint(100)
    return_dict[n_potok] = x**2
    print('Поток №:', n_potok, '    случайное число:', x, ', квадрат числа:', return_dict[n_potok])


if __name__ == "__main__":
    manager = mp.Manager()
    return_dict = manager.dict()

    potoks = []
    for n_potok in range(1, 8):
        p = mp.Process(target=random_x2, args=(n_potok, return_dict))
        p.start()
        potoks.append(p)

    for potok in potoks:
        potok.join()

    print("Результат выполнения расчета:")
    print(return_dict)

Заключение

Мне понравилось экспериментировать с генетическим алгоритмом выведения змеек. Временами, задумывался о том, какой извилистый путь у эволюции в реальном мире, о роли естественного отбора в выживании видов.

Потрясающе, когда из «Ничего», через бесчисленное множество итераций проб, ошибок и побед появляется «Что».

Всем желаю позитива и интересных, продуктивных экспериментов!