
Я не знаю, что такое символьное программирование, но расскажу вам о нем на примере Wolfram Language
Кликбейтный заголовок, риторический вопрос и обещание раскрыть тайну! Не самый лучший набор, но нормального названия для статьи мне в голову не пришло. Что же здесь все-таки будет? Речь пойдет о реализации символьного программирования в Wolfram Language (WL). Я не буду рассказывать про отличия от других парадигм. А также здесь точно не будет общих определений. Вместо этого я попытаюсь ответить на несколько вопросов исходя из своего личного опыта и наблюдений. Вот эти вопросы
Почему все говорят, что WL реализует символьное программирование?
Что такое символьное программирование в WL по мнению респондентов?
Как эта парадигма реализована на самом деле в WL?
Внимание! Я не математик и не знаю haskell и lisp! И буду рад если меня поправят настоящие математики, которые с ними знакомы.
Что думают респонденты?
Я общался на тему символьного программирования с различными людьми напрямую, а так же читал посты, заметки и комментарии. И вот какое усредненное мнение дали мои наблюдения: символьное программирование это такая штука, которая позволяет получать формальные доказательства и совершать аналитические преобразования математических формул в виде кода. Т.е. для примера этот подход отлично работает для вычисления пределов функций. Либо для аналитического решения уравнений. Либо для взятия интегралов и вычисления производных. В общем все то, чем в повседневной жизни пользуются физики и математики.
Так ли это? Отчасти да. Где мы может наблюдать нечто подобное? Например, в замечательной библиотеке SymPy для языка программирования Python. На Хабре есть множество статей посвященных этой библиотеке. Мне например попадались статьи "Символьные вычисления средствами Python. Часть1. Основы" и "SymPy и симуляция физических процессов", где все довольно подробно объяснено. Большинство других статей и руководств к этой библиотеке акцентируют свое внимание именно на решении математических или логических задач. А пользователи видят применение символьному программированию только для решения задач математического анализа - т.е. аналитическое решение уравнений, взятие интегралов и т.д. На мой взгляд это слишком ограниченная точка зрения.
С чего все началось?
Мы будем говорить о WL и все примеры кода будут на нем. Раньше Mathematica преподносилась как система компьютерной алгебры. И действительно вышло так, что она началась именно с решения аналитических задач. Первое, что рассказывают студентам математических и физических специальностей - это то, как использовать Mathematica для работы с алгебраическими выражениями. Вот простейший пример:
Simplify[(x + 1)*(x - 1)]
(* -1 + x^2 *)Что делает эта функция? Очевидно она упрощает символьное выражение! Я уверен, что многие слышали про такие возможности WL. А вот еще пример:
D[x^2 + x + 1, x]
(* 1 + 2 x *)Эта функция дифференцирует символьное выражение по указанной переменной. В чем красота этих двух строчек кода? В том, что мы никак не объявили переменную x. Мы можем написать любой полином или формулу так, как если бы делали это в тетради на уроке математики. И оно будет работать! Кажется, что это очень просто и не имеет никакой реальной пользы, но давайте рассмотрим концепцию более подробно.
Атомы и выражения
Примеры кода выше - это выражения. В частном случае они представляют собой алгебраические выражения, которые, как я уже неоднократно повторял, нужны математикам. Выражение в WL - это составной объект, который можно сконструировать из других объектов, либо из примитивных типов - атомов. Всего существует 6 атомарных типов. Вот они:
Integer- целое числоReal- действительное число с плавающей точкойRational- рациональное число в виде отношения двух целыхComplex- комплексное числоString- строкаSymbol- собственно символы, ради которых мы все здесь собрались.
Больше ничего в Wolfram Language нет. Абсолютно все выражения и конструкции языка представляют собой древовидную структуру состоящую из атомов. Как я могу это проверить? Очень просто, в WL есть функция, которая отображает выражение в виде синтаксического дерева так, что в узлах дерева располагаются только атомы:
TreeForm[a + b + c]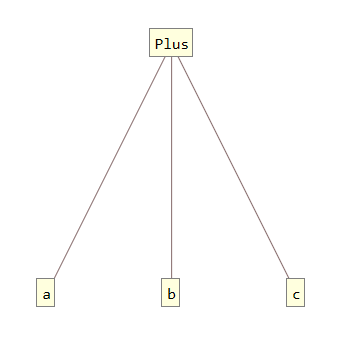
Слева представлено почти самое простое выражение, которое можно создать на WL. Проще будет только f[]. На нулевом уровне у него находится функция Plus, а на первом уровне три переменные, к которым эта функция применена. И каждый узел дерева является символом. Давайте посмотрим как выглядит что-нибудь более сложное:
TreeForm[Sin[Pi] + Sqrt[a + 2] - x^2 / z]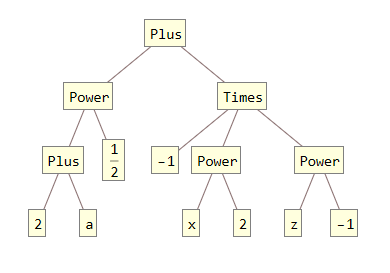
Ого, здесь уже не только символы но и числа. И все равно мы получили древовидную структуру. Кроме чисел и необъявленных переменных - символов, здесь так же есть функции для сложения, умножения и возведения в степень. Правда почему-то нет вычитания, деления и корня. Дело в том, что они однозначно выражаются через обратные операции. Sqrt[x] заменяется на Power[x, 1/2], т.е. по сути на x^1/2, а x - y заменяется на Plus[x, Times[-1, y]], т.е. на самом деле вычитание - это прибавление отрицательного числа. А если это не число, а выражение или символ, то чтобы получить его - мы просто умножаем все на -1. Вы обратили внимание, что арифметическиt операции тоже располагаются в узлах дерева и отображаются как символы? Все потому что они ими и являются. Все арифметические операции это просто функции языка, которые имеют псевдонимы для более короткой записи. Вот несколько примеров:
a + b === Plus[a, b]a * b === Times[a, b]a ^ b === Power[a, b]a && b === And[a, b]a || b === Or[a, b]
Такой способ хранения внутренних объектов языка дает полный доступ ко всей структуре любого выражения. Это означает, что мы можем менять части выражения, удалять и добавлять. Давайте посмотрим на простой пример. Создадим переменную и сохраним в нее выражение:
expr = a * b + c ^ dКак оно выглядит в ядре WL:
TreeForm[expr]
А теперь при помощи функции Part (expr[[i]]) попробуем извлечь части этого выражения. Если мы указываем индексы больше нуля, то извлекаем части внутри квадратных скобок - это тело выражения. Если мы берем нулевую часть - то нам возвращается то, что стоит перед квадратными скобками - это называется заголовок выражения. Еще заголовок можно получить при помощи функции Head.
expr[[0]]
(* Plus - заголовок *)
expr[[1]]
(* a*b == Times[a, b] - первая часть тела*)
expr[[2]]
(* c^d == Power[c, d] - вторая часть тела *)
expr[[1, 0]]
(* Times - заголовок первой части *)
expr[[1, 1]]
(* a *)
expr[[1, 2]]
(* b *)А так же мы можем присвоить новое значение части вот так:
expr[[1, 1]] = e;
expr[[1, 0]] = Power;
expr[[2]] = f;
TreeForm[expr]
Мы изменили выражение напрямую. Более того, мы заменили не только сами переменные, но и функции, которые к ним применены! Не в первый раз я уже использую слово заменили. Выше я использовал внутренние индексы, т.к. точно знал, что и в какой части синтаксического дерева располагается. Что если я не знаю, что внутри, или структура дерева намного больше? Для этого есть специальный синтаксис, который позволяет заменять части выражения не по расположению, а по значению! Это функции Rule и ReplaceAll. У них есть сокращенные записи:
Rule[a, b] === a -> b
ReplaceAll[a, b] === a /. bИ вот как они применяются:
expr
(* e^b + f *)
expr /. b -> g
(* e^g + f *)Выше мы заменили показатель степени. В сокращенной форме синтаксис легко читается как заменить в выражении слева от /. по правилу справа все встречающиеся символы b на символ g. Это и произошло. То, что мы сейчас пронаблюдали - это применение правила замены. Опять же, я очень долго тяну и никак не дойду до сути, но нам нужно запомнить эту штуку. Так как символы, правила и замены это САМАЯ важная часть языка Wolfram.
Давайте посмотрим на правила замены в других примерах. Допустим, я знаю правила дифференцирования простых функций. И я могу записать их вот так:
diffRules = {
Sin[x] -> Cos[x],
Cos[x] -> -Sin[x],
x^2 -> 2*x,
x -> 1,
Log[x] -> 1/x
}; Здесь фигурные скобочки просто означают список элементов. По сути я записал набор правил для дифференцирования. Где слева от стрелочки то, что мы дифференцируем, а справа то, что получаем. При этом и слева и справа записаны символьные выражения - то есть по сути это древовидные структуры из 6 типов атомов. По правде говоря и сам список правил и символ стрелочки - это такие же выражения. Теперь попробуем записать какое-нибудь выражение:
expr = Sin[x] - x^2 + Log[x]И применим к нему правила дифференцирования
expr /. diffRules
(* 1/x - 2 x + Cos[x] *)Все сработало! Мы продифференцировали функцию по нашим правилам!
Шаблоны
Теперь другой пример. Допустим у меня есть выражение:
expr = a^2 + 3 * b^3 - c^4 + 2 * x^2 - x + 4*c + 3И я хочу это выражение линеаризовать, т.е. отбросить все степени выше первой. Я могу сделать это напрямую, как в примерах выше:
expr /. {
a^2 -> 0,
b^3 -> 0,
c^4 -> 0,
x^2 -> 0
}
(* 3 + 4 c - x *)Но это слишком неудобно. Что если я не знаю ни точную степень, ни имя переменной? Как просто указать, что нужно заменить все места, где встречается возведение в степень на ноль? Это можно сделать при помощи шаблонов вот так:
expr /. Power[_, _] -> 0
(* 3 + 4 c - x *)Либо вот так:
expr /. _ ^ _ -> 0
(* 3 + 4 c - x *)В примерах выше я использовал символ подчеркивания так, будто бы это регулярное выражение в строке или безымянный символ, который означает "все что угодно". Это подчеркивание называется шаблоном. Мы использовали самый простой типа шаблона из всех существующих. Для того, чтобы лучше понять, что я умею ввиду - я скажу, как правильно прочитать последний код: заменить в выражении слева все внутренние подвыражения вида "любое выражение" в степени "любое выражение" на ноль. Для работы с шаблонами существует еще одна полезная функция, которая называется MatchQ. Она позволяет сравнить любое выражение на соответствие с шаблоном. Вот как она работает:
MatchQ[a^b, _^_] (* => True *)
MatchQ[f[x[y[z], g], h], _] (* => True *)
MatchQ[g[f], f[_]] (* => False *)То есть первым аргументом идет само выражение, а вторым шаблон, который "накладывают" сверху, чтобы понять соответствуют они друг-другу или нет. И получается, теперь мы можем понять как примерно сработала линеаризация в предыдущем примере. Ядро математики начиная сверху вниз спускается к самым дальним уровням и оттуда постепенно поднимается вверх. Затем на каждом узле происходит сравнение с шаблоном при помощи MatchQ. Если возвращается True, то текущий узел заменяется по указанному правилу.
Шаблоны могут быть более сложными. Их можно встроить в любое место выражения. Например вот так можно проверить, что математическая формула соответствует уравнению физического маятника:
MatchQ[x''[t] + w * x[t] == 0, _''[_] + _ * _[_] == 0]
(* True *)Есть еще множество видов шаблонов. По сути шаблоны можно назвать внутренним подъязыком для Wolfram Language. Например, вот так можно проверить, что выражение соответствует списку из двух целых элементов:
MatchQ[{1, 2}, {_Integer, _Integer}]
(* True *)А вот так проверить, что массив представляет собой чередующееся значения комплексных и рациональных чисел:
MatchQ[{1/2, I, 1/3, I/2}, {PatternSequence[_Rational, _Complex]..}]А еще шаблоны можно именовать вот так:
MatchQ[{1, 2, 1}, {x_, y_, x_}]
(* True *)
MatchQ[{1, 2, 3}, {x_, y_, x_}]
(* False так как указав имя говорим, что первый и третий элемент
хоть и могут иметь любое значнеие, но должны совпадать *)В принципе перечисленного достаточно, чтобы перейти к следующему шагу.
Переход к функциям
До сих пор мы игрались именно с тем, о чем я сказал в самом начале - то есть простенькие задачки из математического анализа. Выше я заявил, что символьное программирование - это не только решение дифур и аналитические интегралы. Но пока ничего другого уважаемые читатели так и не увидели! Что ж.. у нас на данный момент есть:
6 типов атомов
Синтаксические деревья состоящие из них и только из них
Правила и замены
Шаблоны
Причем стоит учесть, что правила, замены и шаблоны - это тоже выражения состоящие из атомов. Как из всего этого создать функцию? Давайте рассмотрим на примере сортировки пузырьком. Создаем выражение из символа и чисел:
arr = {1, 0, 1, 0, 0, 1, 0}Создаем правило сортировки:
sortRule = {first___, 1, 0, rest___} :> {first, 0, 1, rest}И применим это правило один раз к массиву:
arr /. sortRule
(* {0, 1, 1, 0, 0, 1, 0} *)Одна пара поменялась местами! А что если применить правило замены еще несколько раз:
arr /. sortRule /. sortRule /. sortRule /. sortRule /. sortRule /.
sortRule /. sortRule /. sortRule
(* {0, 0, 0, 0, 1, 1, 1} *)Тогда мы получим полностью отсортированный список! Как это можно сделать для любых чисел? Нам понадобится повторяющаяся замена ReplaceRepeated ( //. ) и условие применения Condition ( /; ) и вот код стандартной пузырьковой сортировки:
bubbleSortRule = {f___, x_, y_, r___} :> {f, y, x, r} /; y < xВот как этот код будет работать:
{1, 2, 3, 4, 3, 2, 1} //. bubbleSortRule
(* {1, 1, 2, 2, 3, 3, 4} *)В общем-то все готово. Осталось только сказать ядру WL, чтобы он применял это правило замены всякий раз к любому выражению, которое нужно отсортировать. Мы можем сделать это при помощи стандартного синтаксиса языка Wolfram:
bubbleSort[arr_List] := arr //. bubbleSortRule
bubbleSort[{1, 2, 3, 4, 3, 2, 1}]
(* {1, 1, 2, 2, 3, 3, 4} *)Выше мы создали функцию. Но как мы это сделали? Слева от знака := находится шаблон!! А справа находится выражение! Подождите, ведь это же слишком похоже на то, что создание функций - это просто процесс добавление в ядро пар шаблон + правило замены! Точно так же, как у нас выше было сделано для bubbleSortRules! Просто там мы вызывали замену самостоятельно, а здесь за нас это делает ядро! Как я могу это доказать? Очень просто! Я знаю где находится хранилище с определениями функций. Это хранилища совершенно неожиданно тоже является символом и называется DownValues:
DownValues[bubbleSort]
(* {HoldPattern[bubbleSort[arr_List]] :> (arr //. bubbleSortRule)} *)Да мы это только что обсуждали! Это такое же шаблон и правило замены. Используются чуть-чуть другие функции, но их назначение тоже самое. Давайте возьмем напрямую этот шаблон и попробуем понять чему он соответствует:
MatchQ[
myFunc[{1, 2, 3}],
HoldPattern[myFunc[arr_List]]
]
(* True *)То есть ядро математики сравнивает ЛЮБОЙ пользовательский ввод с шаблоном, который обернут в HoldPattern и если результат сравнения True, то пользовательский ввод заменяется по указанному правилу! Т.е. ядро в автоматическом режиме делает вот так:
myFunc[{1, 2, 3}] /. HoldPattern[myFunc[arr_List]] :> Total[arr]
(* 6 *)Это полностью равнозначно созданию и вызову вот такой функции:
myFunc[arr_List] := Total[arr]
myFunc[{1, 2, 3}]
(* 6 *)Ну и причем здесь символьное программирование?!
Наконец мы дошли до этой секции. Еще раз резюмируя все то, что я написал выше. Символьное программирование - манипуляции с символьными выражениями, где переменные или символы могут не иметь конкретных значений, а использоваться как есть. Это очень полезно в задачах математического анализа и по моим представлениям появилось именно с целью их решения.
Но как реализовано символьное программирование конкретно в WL? При помощи древовидных выражений состоящих из атомом, шаблонов и правил замен! Но что мы знаем теперь? Внутреннее хранилище определений ВСЕХ функций языка это точно такие же шаблоны и правила замены, которые работают с символьными выражениями! Абсолютно весь язык построен на такой модели выполнения. Там конечно же есть дополнительные тонкости, но основа языка заключается именно в последовательном применении правил замены к символьным древовидным выражениям.
Преимущество Wolfram Language и Mathematica в том, что такая концепция вычисления выражений в стенах WRI развивается уже долее 35 лет. Движок для работы с выражениями за это время стал очень мощным и производительным. Настолько, что скорость выполнения аналогичных функций вполне сравнима с другими популярными языками программирования, вот только выполнение абсолютно всех программ в нем идет совершенно неоптимальным способом! Да, разбор синтаксического дерева не такая уж редкая вещь, но бесконечно применение правил замен - это довольно необычная модель, согласитесь?
Не только DownValues
Внутреннее хранилище функций языка имеет и другие разделы. Вот самые основные из них:
OwnValues- переменныеx, y, z, ..DownValues- функцииf[x, y, ..]UpValues- переопределенияg[f[..]]SubValues- многоуровневые функцииf[x][y]..
4 хранилища выше покрывают все возможные виды конструкций, которые можно составить из символов и квадратных скобочек. Есть другие менее важные внутренние разделы, но нам они пока что не интересны. Давайте лучше рассмотрим как происходит выполнение кода.
По ветвям дерева
Когда ядро Wolfram Language, т.е. интерпретатор языка встречает любое выражение на своем пути, то тут же начинает его вычислять. Как это происходит? Пусть мы открыли консоль ядра и написали вот такую строчку:
f[x_, y_] := x^2 - yСначала выполняется первая строка - создается определение и в списке DownValues появляется вот такое правило:
DownValues[f]
(* {HoldPattern[f[x_, y_]] :> x ^ 2 - y} *)Затем вызываем эту функцию:
f[2, 3]Эта строчка в неизменном виде (в данном случае) попадает в ядро. Далее ядро при помощи внутреннего матчера быстро пробегается по всем сохраненным шаблонам и находит, что:
MatchQ[f[2, 3], f[x_, y_]] === TrueТогда в текущем положении стека вызова происходит замена:
f[2, 3] :> 2 ^ 2 - 3Полученное выражение приводится вот в такую полную форму:
Plus[Power[2, 2], -3]Нам удобнее посмотреть на него в древовидной форме:

Затем интерпретатор начинается спускаться от корня к ветвям этой древовидной структуры до самого конца. Последний уровень - это два целых числа 2 и 2. Когда интерпретатор достигнет их он поймет, что это атомы. Причем эти атомы являются числами, а значит не хранят определений. С этого момента ядро начинает подниматься наверх. Сначала оно встречает на своем пути вот такую функцию:
Power[2, 2]Точно так же отправляется в DownValues и ищет определение и с помощью правила заменяет Power[2, 2] :> 4. Тогда древовидная структура становится вот такой:

Поднимаемся еще на уровень вверх, ищем определение Plus и выполняем замену выражения Plus[4, -3] :> 1. В результате у нас остается только один атом без определения, который и возвращается.
Если во время движения по синтаксическому дереву на каком-то узле встречается символ, у которого нет определений, то та часть дерева, которая была под ним и выполнилась остается неизменной. Это же выражение в неизменном виде передается интерпретатору дальше. И это же выражение как полноценный объект используется в дальнейших вычислениях. Допустим я пытаюсь выполнить вот такой код:
1 + g[2, 3 + 4, 5 - 6^7]В древовидной форме код выше выглядит вот так:
TreeForm[Hold[1 + g[2, 3 + 4, 5 - 6^7]]]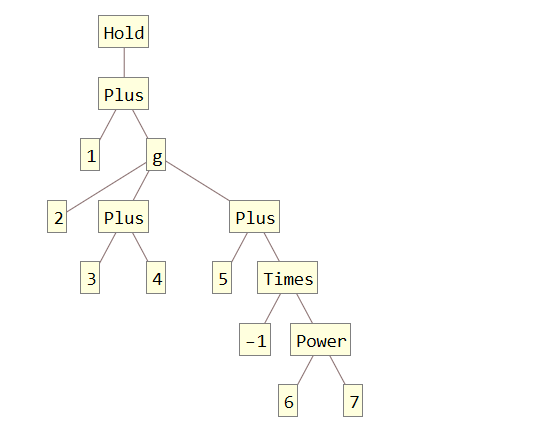
Мы знаем, что у g нет определений, значит в результате выполнения это небольшое выражение должно остаться. И вот как выглядит результат:
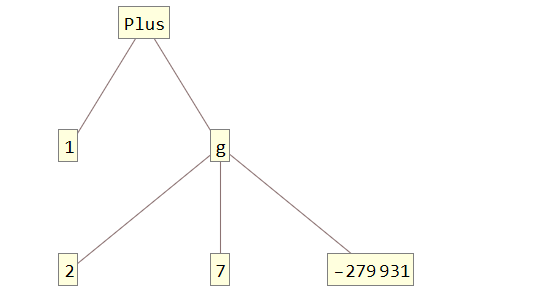
Т.е. узел с g не был ни на что заменен. А функции, которые являются заголовком для g ничего не смогли сделать, так как у них нет определений на этот случай. В итоге одно символьное выражение преобразовалось в другое. А все преобразования производились внутри ядра при помощи правил замен.
В чем же магия этого подхода?
Вся уникальности работы с кодом как с синтаксическим деревом заключается в полном доступе к этому самому коду. Если я знаю где хранятся определения, я могу их извлекать, анализировать и изменять прямо на ходу. А так же я могу эти же определения пересылать по интернету, сохранять в файл, экспортировать в языки разметки или преобразовывать в другие языки программирования!
Но конечно же всегда лучше рассматривать конкретные примеры. Как при помощи символьного программирования добавить логирование для любой функции, но при этом не затронуть все остальные. Задача очень проста: у меня есть сложный код и там вызывается много функций, но при этом он просто выполняется и возвращает результат. Я хочу сделать так, чтобы во время вызова одной конкретной функции кусок кода внутри этой функции напечатал дополнительный лог. Вот моя функция:
ClearAll[numberInterpreter]
numberInterpreter = Interpreter["Number", NumberPoint -> ","];
ClearAll[currencyToAssoc]
currencyToAssoc[
XMLElement[
"Valute", {"ID" -> id_}, {XMLElement["NumCode", _, {numCode_}],
XMLElement["CharCode", _, {charCode_}],
XMLElement["Nominal", _, {nominal_}],
XMLElement["Name", _, {name_}],
XMLElement["Value", _, {value_}], ___}]] := <|"CurrencyId" -> id,
"CurrencyCode" -> numberInterpreter[numCode],
"CurrencyIso" -> charCode, "Nominal" -> numberInterpreter[nominal],
"Name" -> name, "Rate" -> numberInterpreter[value]|>
ClearAll[currencyRates]
currencyRates[] :=
Module[{request, response, bodyByteArray, body, xml, result},
request = HTTPRequest["http://www.cbr.ru/scripts/XML_daily.asp"];
response = URLRead[request];
bodyByteArray = response["BodyByteArray"];
body = ByteArrayToString[bodyByteArray, "WindowsCyrillic"];
xml = ImportString[body, "XML"];
result =
Map[currencyToAssoc]@
FirstCase[xml, XMLElement["ValCurs", _, rates : {__} ..] :> rates];
Return[result]]Название функции говорит самом за себя - она просто получает курсы валют с сайта центрального банка. Вот как ее можно вызвать:
currencyRates[]В результате мы получим вот такой список курсов валют:
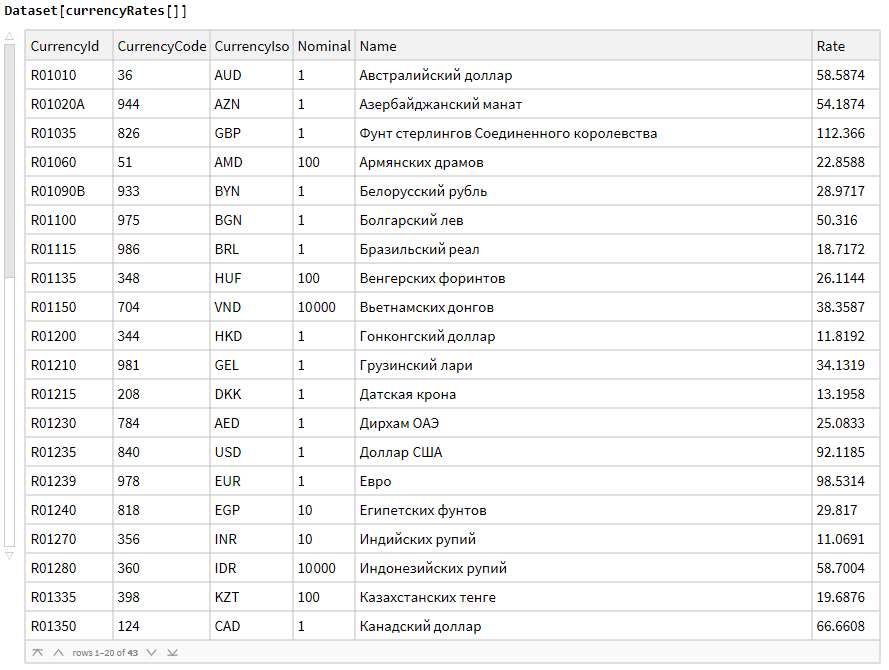
Но что будет если у меня есть такая функция, я не могу ее менять, но при этом хочу вставить в середину ее кода логирование? Например печатать HTTPRequest везде где он используется. Вот как это я могу сделать:
DownValues[newCurrencyRates] = DownValues[currencyRates] /. {
currencyRates :> newCurrencyRates,
HoldPattern[HTTPRequest[data___]] :> Echo[HTTPRequest[data], "Request"]
}И теперь вызовем функцию повторно:
Dataset[newCurrencyRates[]]
Теперь вместе с результатом напечатался и объект с HTTP-запросом, который мы отправили. Т.е. мы только что внедрили дополнительное действие непосредственно в код сторонней функции. Пусть конкретно эта демонстрация не выглядит впечатляющей, но сами возможности изменить любой код в любой момент разобрав синтаксическое дерево очень впечатляют.
Мета-программирование
В популярных языках программирования очень часто для пользователя есть доступ к внутренней структуре кода через рефлексию. В WL никакой рефлексии по сути нет, так как нет каких-то определенных функций для взаимодействия со структурой языка. Ведь нет никакой разницы между данными и кодом. С кодом можно работать точно также как и с данными. И один из примеров применения этой концепции - это простая кодогенерация. Имея набор данных можно естественным образом без вызова специальных функций языка превратить данные в определения функций. Причем сделать это по сути можно любым подходящим способом. Как через создание DownValues напрямую, так и с помощью превращения строки в выражение, так и создавая определения классическим способом. Пусть у нас есть строка с описанием методов и параметров:
apiSchema = "{
\"paths\": {
\"method1\": {\"x\": \"number\", \"s\": \"string\"},
\"method2\": {\"d\": \"timestamp\"}
}
}"Мы можем ее импортировать:
paths = ImportString[apiSchema, "RawJSON"]["paths"]
(* <|"method1" -> <|"x" -> "number", "s" -> "string"|>,
"method2" -> <|"d" -> "timestamp"|>|> *)Теперь создаем функцию-генератор. Т.е. ту функцию, которая из набора данных конструирует другое определение:
makeMyApiFunc[methodName_String, paramsData_Association] :=
With[{method = ToExpression[methodName],
params =
KeyValueMap[
Pattern[#1, Blank[#2]] /. {number -> Real,
timestamp -> DateObject, string -> String} &] @
Association @
KeyValueMap[ToExpression[#1] -> ToExpression[#2] &] @
paramsData
},
Evaluate[method @@ params] = apiFunc[methodName, paramsData]
]Применим эту функцию к набору данных:
KeyValueMap[makeMyApiFunc, paths]После чего в текущей сессии будет создано определение:
?method1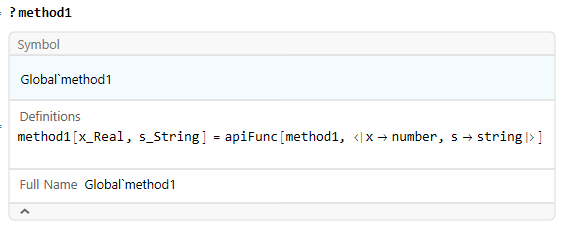
Выводы
Вместо выводов краткая констатация ответов на вопросы из самого начала.
Язык Wolfram действительно реализует символьное программирование, но большинство считает, что это относится только к алгебраическим выражениям и аналитическим задачам.
Символьное программирование изначально зародилось как инструмент для аналитического решения математических задач. В том числе сам язык Wolfram появился благодаря этому. Поэтому "по старой памяти" многие люди, которых я знаю лично символьным программированием называют только подкласс задач связанных с математическим анализом
Но на самом деле весь язык Wolfram построен всего лишь из трех основных блоков: символьные выражения, шаблоны и правила замены. И именно эти три возможности делают язык таким, какой он есть - т.е. полностью символьным языком.
Исторический экскурс
Фундаментальная работа Стивена Хьюговича Вольфрама A New Kind of Science посвящена клеточным автоматам. Именно клеточные автоматы являются прототипом той самой модели выполнения кода, о которой я писал выше. Клеточный автомат - например игра жизнь - по сути во время своей работы заменяет один набор байт на другой. Все этим шаблоны и правила замены работают точно так же, только набор байт здесь отображается в виде имени символа или шаблона, а правила применяются точно так же.
Лично я как большой поклонник WL считаю, что вся эта идея, реализация языка и сам дизайн языка программирования Wolfram абсолютно гениален. Я отлично знаю про все его проблемы и недостатки, но все равно считаю, что это язык программирования с лучшим дизайном, который я когда либо видел.
Всем спасибо за внимание!
Комментарии (82)

Refridgerator
14.11.2023 03:06+4Концепцию символьного программирования лучше начинать изучать через нормальные алгоритмы Маркова, и ещё лучше - самому написать для них интерпретатор (это просто).

KirillBelovTest Автор
14.11.2023 03:06+3К своему стыду во время написания статьи я не вспомнил про алгоритмы Маркова. Вы абсолютно правы на счет того, что это лучший теоретический пример символьного программирования. Но хочу сказать, клеточные автоматы, которыми вдохновлялся Стивен Хьюгович и алгоритмы Маркова это практически одно и тоже. Только автоматы чуть-чуть более примитивные. На самом деле всю концепцию исполнения кода в WL точно так же можно свести к нормальным алгоритмам Маркова, чего я к сожалению в статье не показал, но если я найду в себе силы - то отредактирую статьи и продемонстрирую это

youngmysteriouslight
14.11.2023 03:06+2А мне не понятно, почему вы оба говорите именно про алгорифмы, а не про λ-исчисление или комбинаторную логику. По моему мнению, после λ и CL работать с алгорифмами — боль и страдание. Может, поэтому все известные мне современные (кто-то ещё использует Рефал?) системы, которые пробовали в том или ином виде реализовывать определяемые пользователем алгорифмы, обмазываются императивщиной и побочными эффектами: Wolfram, TeX, sed.

KirillBelovTest Автор
14.11.2023 03:06Очень интересно, а можете привести какой-нибудь пример? Как я сказал в самом начале - буду рад объяснению от математика

youngmysteriouslight
14.11.2023 03:06+1Возьмём к примеру CL. В ней выражения (комбинаторы) применяются к другим выражениям, применение всегда одноаргументно. У каждого комбинатора есть комбанаторное свойство, которое определяет, как он будет вычисляться. Например, есть комбинатор I со свойством I[x] = x; или комбинатор K со свойством K[x][y] = x, или S[x][y][z] = x[z][y[z]].
Объекты, свойства, понятия, процессы в предметной области соответствуют своим комбинаторам. Какие-то комбинаторы просто постулируются вместе со своими свойствами, какие-то можно определить через другие (но определение должно сохранять комбинаторное свойство!), какие-то мы оставляем «неопределёнными», то есть рассматриваем их как переменные. Последние в будущем будут заменены на конкретные выражения, когда данные подъедут. Или нет.
Возьмём алгорифм Маркова. Если я работаю с матрицами, какая подстрока или какое правило соответствует понятию «матричное умножение двух неких матриц A*B»? Если я к программе добавлю ещё какие-то правила, будет ли это же (правило или подстрока) соответствовать ровно тому же понятию? Едва ли. Посмотрите, как всю программу приходится переписывать ради того, чтобы дописать другую подпрограмму.

mayorovp
14.11.2023 03:06У вас ссылка битая...

youngmysteriouslight
14.11.2023 03:06@BoomburumУ нас проблема. Я вставляю в decoded-формате, а хабр автоматом конвертирует в не-пойми-что.
http://cs.mipt.ru/wp/wp-content/uploads/2016/02/%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%84%D0%BC%D1%8B-%D0%9C%D0%B0%D1%80%D0%BA%D0%BE%D0%B2%D0%B0.pdf
По теме: можете сами поискать «композиция алгорифмов маркова» — это алгоритм переписывания алгорифма так, чтобы к нему можно было дописать другой алгорифм.

mayorovp
14.11.2023 03:06Похоже, проблема на самом деле где-то ещё: ссылка не изменилась, а файл по ссылке появился. Я бы предположил кривое зеркалирование или кривой CDN, кабы не тот факт, что на домене cs.mipt.ru всего 1 IP и голый Апач.

KirillBelovTest Автор
14.11.2023 03:06Те примеры, которые вы описали вполне выполнятся в WL и будут работать прям в таком виде. Вам ничто не мешает писать практически так же на WL. Разве что указать, подчеркивание добавить, чтобы указать, что x - аргумент.
Вот допустим вы задаете комбинатор и говорите, что при его встрече CL возвращает другой комбинатор. Так это ведь в точности тоже самое, что и правила замены, просто там больше синтаксического сахара и может быть больше одного аргумента.

youngmysteriouslight
14.11.2023 03:06+2Ну так я и не утверждал, что на WL невозможно такое написать. Можно, но для этого надо выработать определённую дисциплину: на каждый символ приходится не более одного определения (Set, SetDelayed), все определение должны идти строго перед запуском вычислений и быть строго на верхнем уровне программы, нельзя использовать никакие «опасные» функции (Print, Set, Function, Module) в качестве комбинаторов и т.д. и т.п.
Проблема в том, действительно ли перед нами комбинатор или это выражение мимикрирует под комбинатор, но таковым не является. WM принципиально не позволяет ответить на подобные вопросы; из ниоткуда может в любой момент вычислений вылезти побочный эффект (самый неприятный для отладки — доопределение символов более специфичными правилами, которые не соответствуют семантике основного правила). Ставится крест на принципе Черча-Россера (результат вычисления не зависит от стратегии) и на ссылочной прозрачности (любое выражение может быть заменено на эквивалентное, полученное в результате вычисления).
P.S. моё предыдущее сообщение относилось к обсуждению алгорифмов Маркова, которые я считаю достаточно плохим формализмом по сравнению с другими. Те же λ-исчисление или комбинаторную логику можно использовать вот прямо как есть, это не «Тьюрингова трясина», хотя сложные программы на них не напишешь. Писать алгорифмы Маркова для решения хотя бы простой практической задачи нереально. «Change my mind»

KirillBelovTest Автор
14.11.2023 03:06В качестве рассуждения, я могу сказать, что вы всегда можете реализовать один собственный символ - Combinator и повесить на него все ограничения связанные с комбинаторной логикой в том виде, какая она есть в Lisp. Но почему нельзя создавать определения в процессе выполнения и чем опасны Print, Module, Function и Set?

ptr128
14.11.2023 03:06+2кто-то ещё использует Рефал?
Как бы Вам не нравилась "имперетивщина", проблема в том, что на практике символьные вычислений все равно тесно сочетаются с численными методами. А тут уже от Рефал толку мало.
Если нужна не смесь символьных вычислений с численными методами, вот тогда используйте язык формальной математики (включая лямбда-исчисление и CL). Например, Isabelle, написанную на ML и Scala.

Sorlak
14.11.2023 03:06+3Подскажите, пожалуйста, а чем отличается "символьное программирование" от встречающихся терминов "символьные вычисления" и "символьная математика"? Если есть "символьное программирование" (реализующее символьные преобразования математических выражений), то можно ли тогда говорить о "численном программировании" (как реализующем численные методы решения уравнений, например)? Или это всё-таки способ вычислений, реализуемый в рамках какой-либо парадигмы программирования?

KirillBelovTest Автор
14.11.2023 03:06Вообще в моей голове сложилось такое мировоззрение, что символьное программирование - это одна из парадигм - такая же как функциональное программирование или ООП. По своим личным наблюдениям я могу только сказать, что оно более редкое, а поэтому менее освещенное. И я еще раз постараюсь кратко сформулировать свою мысль. Чаще всего символьное программирование подразумевает аналитические преобразования математических выражений. По крайней мере так это в популярных библиотеках, которые я встречал. Для этого же в большинстве случаев использую Haskell. Но весь язык Wolfram построен на этой концепции. В нем все является выражением, а исполнение кода происходит при помощи применения правил замен. В комментарии выше @Refridgerator говорил об алгоритмах Маркова, я в конце статьи упомянул про клеточные автоматы - и то и другое является классическим примером символьного программирования. И к тому и к другому можно свести принцип исполнения выражений на языке Wolfram. В общем главная мысль - WL не просто умеет работать с символьными выражениями, а целиком на них построен

mayorovp
14.11.2023 03:06+2Нет тут никакой особой парадигмы, обычное ФП, притом примитивное.

KirillBelovTest Автор
14.11.2023 03:06Какие ваши доказательства? Парадигмы программирования все примитивные и очень простые. Они основываются на нескольких простых принципах. ООП на инкапсуляции, наследовании, полиморфизме и абстракции. ООП код представляет собой в классическом виде объекты, которые обмениваются сообщениями. ФП смещает фокус с объектов, которые обладают "умениями" на действия или функции, которые обрабатывают данные. Символьное программирование концентрируется на преобразовании древовидных выражений при помощи правил замены. Никто вам не мешает писать ФП или ООП код на WL, но вы кажется невнимательно прочитали - я писал про те концепции, которые лежат в основе процесса вычисления кода. То что в большинстве случаев на WL пишут ФП-код - не говорит о том, по каким принципам работает ядро.

mayorovp
14.11.2023 03:06+5Парадигма программирования - она про то, как программист пишет код, а не про то на каких принципах работает ядро.
А правила замены в древовидных выражениях - это в чистом виде паттерн-матчинг из ФП.

rsashka
14.11.2023 03:06+1паттерн-матчинг из ФП
При чем тут ФП? Или паттерн-матчинг нельзя использовать в других парадигмах?

mayorovp
14.11.2023 03:06Запрета на использование его в коде - и правда нет, но вот именно в парадигмы он "не лезет". В автоматной парадигме паттерн-матчингу попросту нет места, в ООП вместо него есть "родные" аналоги, ну а в структурном программировании добавление паттернов в операторы ветвления и цикла всё сильно усложняет (и порой смотрится костылём).
В принципе, символьное программирование как раз могло бы стать той парадигмой, которая также использует паттерн-матчинг - если бы там было что-то кроме паттерн-матчинга.

KirillBelovTest Автор
14.11.2023 03:06+1Для меня наоборот то, что на одном только паттерн матчинге можно построить реальный язык программирования является поразительным фактом. Но все таки, в WL кроме сравнения шаблонов есть и другие важные концепции:
код является данными
все данные (и код) - это древовидные структуры из символов, чисел и строк
вычисление кода происходит при помощи правил замен, а паттерн-матчинг только часть этого процесса

mayorovp
14.11.2023 03:06+1Вот принцип "код является данными" уже интереснее, он и правда в том или ином виде мигрирует между языками и тянет на мини-парадигму. Вопрос только как эту парадигму назвать, название "символьное программирование" не очень-то подходит для этого принципа.
вычисление кода происходит при помощи правил замен, а паттерн-матчинг только часть этого процесса
Как я уже писал, парадигмы - про написание кода, а не про его исполнение.
Возможно, стоит говорить не о парадигме символьного программирования, а об символьном исчислении? Или об исчислениях в принципе, ведь если разобраться, то все исчисления - так или иначе символьные.

KirillBelovTest Автор
14.11.2023 03:06В статье я показал сначала как пользователь может использовать символьное программирование, а затем продемонстрировал, что само ядро работает точно так же. Может чтобы избежать путаницы стоит называть это символьным исчислением

mvtm
14.11.2023 03:06+1код является данными
все данные (и код) - это древовидные структуры из символов, чисел и строк
Поздравляю. Вы узнали про Лисп. То, что указано в этой статье замечательно можно прочитать в старом учебнике "Мир Лиспа" от Хювёнена и Сеппянена

KirillBelovTest Автор
14.11.2023 03:06Скажите пожалуйста, в какой главе этой книги написано про шаблоны и правила замены?

JerryI
14.11.2023 03:06Ну если это примитивное ФП, тогда напишите то же самое на JS скажем

mayorovp
14.11.2023 03:06Так JS ещё не ФП-язык. Наличия функций и замыканий для ФП недостаточно.
А вот на каком-нибудь ClojureScript, думаю, написать что-то похожее проблемой не будет.

KirillBelovTest Автор
14.11.2023 03:06+1Все таки я вас не понял. Если ФП или Символьное Программирование - это про то как программист оформляет свой код, то на JS стопроцентно можно писать как на ФП.

mayorovp
14.11.2023 03:06-2Где на JS паттерн-матчинг?

KirillBelovTest Автор
14.11.2023 03:06+3Я люблю холивары про стили, парадигмы и подходы программирования. Паттерн-матчинг не является синонимом ФП. Главный принцип ФП насколько я понимаю - это акцент на функциях, который обрабатывают данные. Еще важно, что данные неизменяемы - то есть они не могут мутировать как объекты, а функции всегда стабильно возвращают результат. То есть мутирующая операция на изменяемом объекте будет каждый раз менять состояние системы, а преобразование одних данных в другие функцией не должны ничего менять и обязаны что-то возвращать. Нигде я не видел паттерн-матчинг как обязательное условие ФП. Все что я описал выше работает в JS. Вы сами писали - парадигма - это то, как пишет программист. На JS если следить за руками можно легко писать функции, которые не будут ничего мутировать и однозначно возвращать результат. Его поэтому так любят там применять, потому что например в DOM возникает слишком много путаницы если каждая функция будет заниматься мутированием вместо простых и четких преобразований, в которых программист уверен

mayorovp
14.11.2023 03:06-2Парадигмы тоже развиваются, и ФП без паттерн-матчинга давно уже некузявое.
В смысле, писать функции-то можно, только неудобно.

Refridgerator
14.11.2023 03:06WL беспорно революционный язык, однако, раз он до сих пор не стал популярным, то уже и не станет - и понятно почему. Помимо революционных идей там есть и костыли, которыми Стивен подпирал то, что не получилось сделать красиво. В первую очередь это, конечно, квадратные скобки для передачи аргументов в функцию. Во вторую - всё заточено под комплексные числа и даже с обычными кватернионами там работать боль и страдания. Ну и грамматика замен вообще не интуитивно понятная, и выбор символа // для постфиксных вычислений сбивает с толку программистов на си-подобных языках. Поэтому у меня накопилась уже куча идей, как это всё можно улучшить, но реализацию их на практике осознанно оттягиваю до последнего.

KirillBelovTest Автор
14.11.2023 03:06+5Спасибо за ответ. Думаю квадратные скобки и двойной слеш это самая меньшая из проблем. На мой взгляд САМАЯ большая проблема в том, что это проприетарный язык, который 30 лет продавался только за деньги, а когда наконец до Стивена Хьюговича дошло, что опен-сорс двигает технологии вперед - было уже очень поздно.
Я общаюсь с разработчиками ядра и их мнение такое, что в том виде, в котором выпускает язык WRI прямо сейчас у него очень сомнительное будущее, куда больший толчок к развитию он получит в тот момент, когда у кого-то дойдут руки выпустить открытую реализацию языка с возможностью подключения пакетов из реализации WRI.

ptr128
14.11.2023 03:06+4На мой взгляд, главным препятствием к его популяризации стала проприетарная лицензия. Практически все популярные сейчас языки программирования - со свободными лицензиями. И я думаю, что их популярность во многом происходит именно их этого.
Upd. Извиняюсь, не обновил страницу. И в итоге написал тоже самое, что уже было написано до меня.

youngmysteriouslight
14.11.2023 03:06+3WL (точнее, WM) был популярен среди учёных. В широкие массы он не вышел из-за 1) конской цены, по которой он большую часть времени распространялся, когда народ присматривался к этому инструменту, ну и упомянутая другими проприетарная лицензия, и 2) рекламы и позиционирования: Стив его пиарил как шайтан-машинку, которая и тайны мироздания моделирует, или около-человеческую речь понимает, а ещё крестиком вышивать умеет, в то время как рядовому пользователю нужен обычный ЯП общего назначения с низким порогом входа и с хорошей библиотекой для решения его, пользователя, задач (собственно, поэтому Fortran и Python заимели популярность в своё время). Причём WL является таким ЯП, но чтобы Стив так сказал, нужно гордостью подавиться. Посмотри на переводные статьи про WL на хабре — много ли желания возникает использовать его для решения частных бытовых задач?
Костыли, конечно, есть, но это не квадратные скобки. К слову, WL один из немногих языков, в которых группировочные скобки для разбора выражений с инфиксными операторами и скобки, входящие в состав синтаксического выражения (список аргументов, кортеж и т.п.), различаются графически. К примеру, в JS скобки в
x = (a, b)иx = f(a, b)выполняют разную роль.Также
//не проблема, ведь всегда можно использовать префиксную запись.К костылям я бы отнёс императивность интерпретатора, которая вынуждает внимательно следить за тем, в каком состоянии находится ядро (kernel), в т.ч. какие правила записаны в
*Values
Refridgerator
14.11.2023 03:06+11) ну не такая уж и конская цена. Не так уж и давно, до известных событий, лицензия для индивидуального исследователя обошлась мне в 25 т.р. Это в 2 раза меньше суммы, потраченной мной на велосипед далеко не премиум класса, состоящего в основном из алюминиевых труб по технологиям 100-летней давности.
2) с неадекватной рекламой согласен. Для ЯП общего назначения он не подходит просто по определению. Причём, при сильном желании, это тоже можно было реализовать - но для этого Стивен должен быть ещё и программистом, чтобы точно знать, что этим самым программистам нужно для полного счастья.

youngmysteriouslight
14.11.2023 03:06ну не такая уж и конская цена.
Я мог ошибиться, описал субъективное видение из далёкого прошлого. Когда я покинул НИИ и у меня кончилась действующая лицензия, решил купить у них. Единственная подходящая лицензия стоила за год как 1/4 моей месячной зарплаты. Естественно я не стал её приобретать.
Когда на одном из мест работы встал вопрос, а не использовать ли нам Вольфрам, начальство посмотрело и сказало, что потенциальная выгода от языка и стандартной библиотеки не покрывает стоимость и риски, связанные с длительным сопровождением будущих программных компонент на Вольфраме. Деталей не знаю.
Для ЯП общего назначения он не подходит просто по определению.
В текущем виде — да. Впрочем, я на нём и XML-файлы парсил и анализировал, и с файловой системой работал, и строил иллюстрации к статьям, и числодробилку писал. У языка есть потенциал стать вполне хорошим скриптовым языком.

KirillBelovTest Автор
14.11.2023 03:06На самом деле цена действительно очень высокая. Ведь если вы хотите пользоваться всегда новой версией, то придется покупать заново лицензию раз в 1-2 года. Велосипед послужит намного дольше

ekimenkoav
14.11.2023 03:06+1Когда то 3-4 года назад приобрели 2 сетевые лицензии за 2500$. По сравнению с специализированным геофизическим программным обеспечением эта цена не была высокой.
На работе у нас есть сложности с установкой на рабочие станции бесплатного и open-source ПО. В тоже время к установке Wolfram Language вопросов не возникает.

Refridgerator
14.11.2023 03:06+1Там прогрессивная цена, обновление до новой версии стоит дешевле, чем покупать её с нуля. Ну и есть специальный сайт, где можно бесплатно ознакомиться с новыми версиями в течении неопределённого срока. Благодаря которому узнал, что в новых версиях принципиально нового (и необходимого) появляется мало (ну изменился там слегка движок для взятия интегралов, но прям заметной прогрессий не увидел), а вот ухудшений прям достаточно, включая отказ от поддержки старых версий Windows.
Что действительно раздражает - так это политика Вольфрама по непризнанию собственных ошибок. Это когда считаешь интеграл, а в результате пропадает переменная интегрирования или вообще ноль. Или внезапное падение оболочки, или внезапная утечка памяти. Нет у них на сайте списка известных проблем.

KirillBelovTest Автор
14.11.2023 03:06+1как писал @JerryI, на данный момент не смотря на все проблемы и сложности существуют пакеты для WL, которые позволяют писать веб-приложения, ботов для различных приложений, анализировать данные, тренировать нейросети и др... то есть я хочу сказать что силами энтузиастов постепенно в языке появляется то, что интересно программистам и то, что делает WL языком общего назначения. Вот вам чего не хватает чтобы пользоваться WL как языком общего назначения?

ptr128
14.11.2023 03:06Если строго по имеющейся расплывчатой терминологии, то, с одной стороны, любой тьюринг-полный язык можно считать языком общего назначения, а с другой стороны - тот же Rust можно считать предметно-ориентированным языком, так как он разработан для программирования, ориентированного на безопасность.
Можно ли на WL написать модуль ядра Linux? А насколько удобно на C или Rust заниматься символьными вычислениями?
Как по мне "общее применение" или "универсальность" - это всегда множество компромиссов. Я за языки, которые делают что-то очень хорошо в своей области, а не пытающиеся объять необъятное.

KirillBelovTest Автор
14.11.2023 03:06+1Я все таки пытаюсь выяснить про что-то, что есть в популярных языках чего вам не хватает. Я лично раньше все время хотел, чтобы была возможность писать веб-приложения на WL. Теперь я сам это сделал и оно работает. А вам чего не хватает? На Python тоже не пишут ядро операционной системы, но он считается языком общего назначения и есть области где он хорош, а где не очень.

ptr128
14.11.2023 03:06+1Я лишь пытаюсь донести до Вас свое личное мнение о том, что швейцарский нож, конечно круто, но по отдельности нож, отвертка, ножницы, плоскогубцы и шило намного удобней в работе.

Refridgerator
14.11.2023 03:06+1Чего не хватает? ООП, перегрузки операторов, строгой типизации, событийно-ориентированного программирования, дата-ориентированного программирования, параллельного программирования с примитивами синхронизации, средств отладки, скорости исполнения.

KirillBelovTest Автор
14.11.2023 03:06+1Но ведь все это есть, просто оно выглядит необычно и нужно привыкнуть. Но это в любом языке так. С ООП только спорно, но матируемый объекты с наследованием я сделал сам

KirillBelovTest Автор
14.11.2023 03:06Пожалуй про это стоит написать отдельно небольшое руководство.

JerryI
14.11.2023 03:06все уже придумано было из того, что описываете, причем довольно давно. Лет 10 назад всплывали такие вопросы в Google Groups и на них были ответы. Просто люди забыли, или лень было разбираться
и ООП, и шайтан-ФП. В этом и соль, что можно описать диалект языка под задачу и потом уже решать на нему эту самую задачу. Компиляцию в LLVM завезли недавно там хорошая типизация кстати и еще CUDA из коробки, до этого было с помощью CCompiler. Debugger там есть, пусть и так себе на мой взгляд. Если хочется что-то экзотического типа event-loop, он там почти есть из коробки (скажем, сокеты или другие внешние события дергают обработчики асинхронно, можно любую логику и промисы при желании реализовать). Если этого мало, то есть LibraryLink, которая подключит любую произвольную dll и можно наворотить делов в ядре...ух
В общем вероятно ни о чем спорите вдвоём. Минусы у всего есть, как писали выше, универсального бриллиантового тула не выйдет, но ЯП шириной области применения как минимум не уже, чем Python точно выходит. Только своей проприетарностью отличается резко в не самую хорошую сторону.

Refridgerator
14.11.2023 03:06+1все уже придумано было из того, что описываете
Ну давайте будем честными. Далеко не всё из перечисленного, и только то, что хоть как-то ложится на исходную концепцию языка. Веб-сервер можно сделать только потому, что для этого целенаправленно сделали SocketListener и прочую инфраструктуру. А DSP-процессор нельзя сделать, потому что средств для потоковой обработки аудио ещё не завезли.
есть LibraryLink, которая подключит любую произвольную dll и можно наворотить делов
dll же на каком-то другом языке пишется? Соответственно сразу и возникает вопрос, какую часть логики писать на этом другом языке, а что оставить Вольфраму. И лично для меня всё выше перечисленное намного, намного комфортнее делать на си++ или c#. А на Вольфраме - всё то, ради чего он и создавался - вычисления, прототипирования, генерация таблиц или кода, ну или просто как справочник, что само по себе уже немало. Интереснее наоборот, Вольфрам вызывать из c#.
В общем вероятно ни о чем спорите вдвоём
Споры в комментариях увеличивают количество просмотров и двигают статью в топы) Ещё можно заглянуть на WOLFRAM Demonstrations Project и заметить, что демки по оформлению там довольно однообразные.

KirillBelovTest Автор
14.11.2023 03:06А прием здесь демонстрации? Они все были сделаны примерно в одно время, когда WRI придумали CDF и решили сделать сайт с кучей примеров. А лучший пример - это визуализация

KirillBelovTest Автор
14.11.2023 03:06Мы не использовали SocketListener, но его тоже можно использовать в текущей реализации. Но спору нет - без него бы веб-сервер не получился

JerryI
14.11.2023 03:06+1@Refridgerator,я люблю такие вопросы)
SocketListener
@KirillBelovTestнедавно его на помойку выкинул и написал свой
Ещё можно заглянуть на WOLFRAM Demonstrations Project и заметить, что демки по оформлению там довольно однообразные.
Вот кстати есть WLX и там можно разгуляться с оформлением на CSS/HTML
КДПВ Ну и еще вот на том же WL и JS + кастомные сокеты написанный с нуля фроентенд)
А DSP-процессор нельзя сделать, потому что средств для потоковой обработки аудио ещё не завезли.
Да тут трудновато, согласен. Здесь явно нужен модуль на Си/++/ust.
Споры в комментариях увеличивают количество просмотров и двигают статью в топы)
Сложно не согласиться)
dll же на каком-то другом языке пишется? Соответственно сразу и возникает вопрос, какую часть логики писать на этом другом языке, а что оставить Вольфраму.
Да, я лично не спорю. Мне всегда нравилось делать композиты в роде WL + C + OpenCL + HTML/CSS для морды. Я имел ввиду конкретно, что писать ООП и прочие штуки можно, если хочется. Даже если совмещать два языка при разработке, удобнее, когда и там и там есть, скажем, объекты и они передаются бесшовно друг другу (что как раз возможно).

KirillBelovTest Автор
14.11.2023 03:06Ого! Вот это да! Неужели на гифке происходит real time calculation, т.е. в каждый момент времени после обновления кадра браузер получает новые данные для отрисовки и все изменения из UI пересылаются так же? Но ведь мне выше говорили, что WL медленный!!! ;-)

JerryI
14.11.2023 03:06+1Ну все упирается в скорость сериализации данных чтобы отправить их по TCP. А так да

JerryI
14.11.2023 03:06+1Чуток дополню.
Квадратные скобки понятно почему, это чтобы friendly для математических выражений. Раньше было принято что программист также должен являться математиков. А штуки типа // и всякие @ это же сокращения, которые в принципе не обязательны. В целом ну больше косметические вещи описываете, к которым, разумеется может быть очень чувствительно общество
Кстати насчет практических задач. Там в репе @KirillBelovTestесть и веб сервера и телеги ботов зоопарк. Те если забыть про неотделимую стандартную библиотеку и юзать бесплатный Wolfram Engine то будут все бытовые задачи
UPD блин уже ответили ;)

uuger
14.11.2023 03:06+1Про "программиста", кстати, есть статья в Википедии

KirillBelovTest Автор
14.11.2023 03:06Спасибо большое, конечно же я уверен в том, что Хабр все еще торт и уважаемые читатели знают Константина не только как героя популярного мема =)

ptr128
14.11.2023 03:06+5Странно, что в статье не прозвучало ни слова сравнения с динозавром символьного программирования - Lisp. Все же наиболее мощная и известная OpenSource система символьного программирования реализована именно на нем (Maxima)

KirillBelovTest Автор
14.11.2023 03:06+2Как я в самом начале и написал - я не знаю Lisp и поэтому не могу сравнить. Я поверхностно знаком с ним и знаю то, что WL и Lisp очень похожи концептуально. Но я с вами согласен - сравнение Lisp и WL было бы очень полезным делом

ptr128
14.11.2023 03:06+1Не в качестве критики, а в качестве идеи для следующей статьи.
Можно сравнить имеющиеся в WL библиотеки с библиотеками Maxima. Не вдаваясь в детали реализации и в отрыве от языка. Подключить себе в проект Maxima можно даже с весьма поверхностными знаниями Lisp. Хотелось бы представлять, даст ли заметный эффект переход на WL или нет. Например, насколько успешно уже имеющиеся библиотеки решают хотя бы не дифференциальные системы уравнений в обоих системах.

KirillBelovTest Автор
14.11.2023 03:06+1Отличная идея, спасибо! Как только смогу я попытаюсь сравнить WL и Maxima!

belch84
14.11.2023 03:06+1Всегда с опаскою читаю публикации, содержащие слово "парадигма" (на текущий встречается дважды в собственно статье и 18 раз в комментариях), и не очень разбираюсь в различных подходах к программированию (пользовался лишь некоторыми, которые, по-видимому, считаются устаревшими), хотя и написал когда-то систему, в составе которой, среди прочего, имеются процедуры манипулирования символьными выражениями. Понимаю только, что реальные программные системы с трудом можно втиснуть в рамки какого-то одного подхода, и поэтому невозможно делать вообще все, придерживаясь одной универсальной методологии, как не стоит писАть бухгалтерскую учетную систему на Лиспе, решение диффуравнений на Коболе или АСУТП на SQL. Символьные оперции действительно очень часто связаны с численными методами, но заменить собою численные методы они не могут. По-видимому, реальной перспективой является создание средств для взаимного проникновения различных подходов (в виде API), а не совершенствование каждого подхода, чтобы он вытеснил все остальные, как бы заманчиво это не выглядело

ALexKud
14.11.2023 03:06АСУТП на SQL можно написать, промежуточный уровень между контроллерами и верхним уровнем, имхо.

KirillBelovTest Автор
14.11.2023 03:06+1На самом деле я использовал слово "парадигма" чтобы избежать тавтологии, но на Хабре любят обсуждать парадигмы и подходы, так как это такая тема, которая не имеет четкого определения. Если бы я писал более точно, то это было бы во-первых скучно, во-вторых здесь в комментариях не собралось бы столько замечательных людей. Вы правы на счет того, что в один подход невозможно втиснуть абсолютно все. Но этого и нет. Я пытался рассказать только о том, почему WL называют символьным языком программирования. Но это не исключает всего остального. Язык так же называют процедурным и функциональным. А еще на нем можно сделать ООП.
Про последнюю часть вашего комментария. Примерно так я и поступаю на самом деле со своими пет-проектами. Мне нравится делать то, чего в языке еще нет, но очень хочется. Часто я решаю это в виде API стороннему сервису, или в виде использования скомпилированной библиотеки на другом языке. В первую очередь я всегда решаю практическую задачу, но мои предпочтения на стороне WL благодаря его дизайну. Например, я сделал клиент для WebSocket протокола. Им можно пользоваться как в других языках, но с особенностями WL. Вот только конкретно в этой библиотеке я не делал сам протокол, а взял готовую реализацию на Java.

Vytian
14.11.2023 03:06+1Тоже мне, контурные интегралы они выкатили только в версии 13.3, этой зимой, на 35, ядрить их, году существования пакета. В статусе Experimental.
А уж с какой радостью оно ядра роняет и память жрёт, - ни в сказке сказать, ни пером описать, нормальный программист плюнет-разотрет и напишет сам, а ученые да, и не такое терпят.
Их терпят только за то, что остальная сивольная алгебра еще беднее по функционалу, а тут по крайней мере порог входа низкий и можно студентам-непрограммистам задачи ставить, а те могут со стак-оверфлова невозбранно копипастить.

ptr128
14.11.2023 03:06контурные интегралы
остальная сивольная алгебра еще беднее по функционалу
А что не так в Maxima с контурными и поверхностными интегралами?

KirillBelovTest Автор
14.11.2023 03:06+1А можете пожалуйста рассказать какого рода проблемы у вас чаще всего приводили к падению ядра и привести пример кода или хотя бы показать какую задачу вы решали? Ну и про потребление памяти тоже хотелось бы подробнее

JerryI
14.11.2023 03:06+1Понимаю о чем вы частично. Всегда есть альтернативный путь, падает в основном из-за оболочки. Все численные функции очень стабильны, нестабильна динамика (что опять не часть языка а функция фронта) и всякие «опасные» символьные вычисления.
Как скриптовый язык (wolfram engine) он вот уже три года работает на сервере у меня университете и хранит и обрабатывает и показывает через веб морду 1000 (не фигура речи) экспериментальных спектров со всяких машин от одной группы экспериментаторов.
И да, оно падает периодически из за утечки памяти, но на практике местный свитч/роутер чудит примерно с такой же регулярностью
Просто Стив склоняет привязываться к нативной платной блокнотной среде, хотя если забить на это и просто юзать сам язык без стандартных инструментов все идет круто. И фронт при желании можно свой прикрутить (уже сделано, аж три вариации для vscode для jupiter и еще самописный на js). И ничего там не падает.

ababo
14.11.2023 03:06+1Согласно вашему описанию (как я его понял) ядро последовательно сопоставляет шаблоны до тех пор, пока новых подстановок далее не находится. Следовательно, должны отсутствовать взаимно-обратные правила (т.е. A -> B вместе с B -> A) или группы правил (например, A -> B, B -> C и C -> A), иначе может случиться зацикливание. Отсюда я заключаю, что реальный процесс вычисления должен быть сложнее, с возвратами и предотвращением циклов.

KirillBelovTest Автор
14.11.2023 03:06Если есть бесконечная рекурсия - ядро в какой-то момент выдает сообщение о том, что лимит рекурсии исчерпан. Если есть бесконечный цикл, который не удается определить как рекурсию - то вычисления так и будут висеть бесконечно. Это является ответственностью пользователя. Конечно хочется чтобы такое предотвращалось, но вот такой принцип языка

Zenitchik
14.11.2023 03:06+1А можно символьные вычисления для оптимизации регулярных выражений (классических) приспособить?
Есть у меня, положим, тыща альтернатив, я хочу чтобы общие префиксы/постфиксы сами за скобки вынеслись.

KirillBelovTest Автор
14.11.2023 03:06Так быстро мне трудно сказать, но в WL есть очень крутая штука, которая называется StringExtression.
Например такой код проверят что строка соответствует шаблону по первому слову:StringMatchQ["string1 string2", "string1" ~~ __]А вот такая штука вырежет текст из разметки XML:
StringCases["<div>text</div>", "<div>" ~~ text__ ~~ "<div>" :> text]Вот такой проверит на соответствие простому номеру телефона:
StringMatchQ["+79991234568", {"89", "+79"} ~~ NumberString]В строковые выражения имеют примерно такой же функционал как и регулярные выражения, но для меня, так как я ими чаще пользуюсь они более читабельны и позволяют более универсальный код писать для разбора строк.
Может быть позже я напишу про них отдельную статью

Zenitchik
14.11.2023 03:06На множестве регулярных выражений определены: конкатенация и альтернатива. У конкатенеции приоритет. Скобки меняют порядок действий. С ними хотелось бы работать аналогично тому, как мы работаем с выражениями, содержащими умножение и сложение.
А StringExtression можно символьно преобразовывать? Получать из одних StringExtression другие? Выносить за скобки общий префикс или наоборот - раскрывать скобки?

KirillBelovTest Автор
14.11.2023 03:06Ну вообще все это можно делать, только я пока не могу придумать задачу на которой это можно показать. StringExpression точно такое же выражение как и все остальное. В WL есть регулярные выражения, но они классические и представляются в виде строки, поэтому как с символами с ними не поработаешь. У вас есть какой-нибудь пример чтобы я мог показать как можно изменять сами строковые выражения?

Zenitchik
14.11.2023 03:06+1Ну, вот, например:
день ::= \d{1,2}
месяц ::= \d{1,2}
год ::= \d+
годiso ::= \d{4}
месяцiso ::= \d{2}
деньiso ::= \d{2}Дальше я использую ранее определённые элементы как переменные, и записываю множество форматов:
значение ::=
::= день\.месяц\.год
::= месяц\.год
::= год
::= годiso-месяцiso
::= годiso-месяцiso-деньisoДальше я хочу это множество форматов объединить через "|" и оптимизировать полученное выражение выносом за скобки общих префиксов, чтобы я мог визуально посмотреть, что за язык получается.
Собственно, Regex - не принципиально. Если ту же задачу можно сделать с помощью StringExtression - тоже покатит.

deadmoroz14
14.11.2023 03:06Прочитав "символьное программирование", почему-то подумалось что будет что-то про математическую оптимизацию, которая так же называется "математическое программирование". Уж больно там формулировки похожие: линейное, нелинейное, квадратичное, дискретное, целочисленное и т.д., и всё программирования. Тем более, что символьные вычисления там очень даже используются.
Касательно самой статьи: спасибо, интересно, но ничего кардинально нового не увидел (впрочем, чего ещё ожидать от языка 30+ летней давности). Сейчас есть языки и поинтересней. В той же Julia можно и традиционными символьными вычислениями заниматься (на базе символов), так и то же самое проделывать с кодом (привет лисп). Плюс метчинг на базе системы типов через multiple dispatch. Можно сделать всё то же самое, что здесь, и даже больше, да ещё и быстрее.

JerryI
14.11.2023 03:06+1спасибо, интересно, но ничего кардинально нового не увидел (впрочем, чего ещё ожидать от языка 30+ летней давности). Сейчас есть языки и поинтересней.
Спору нет. Есть новые и старые sexy языки. Это чисто вкусовщина
Можно сделать всё то же самое, что здесь, и даже больше, да ещё и быстрее.
Вероятно вы очень плохо знакомы с WL, что в принципе неудивительно, так как статья только верхушку айсберга затрагивает. Благо @KirillBelovTestеще напишет для интересующихся. «Тоже самое и даже больше» - тут как черное назвать белым)

KirillBelovTest Автор
14.11.2023 03:06Можно сделать всё то же самое, что здесь, и даже больше, да ещё и быстрее.
А что больше-то? Можете пожалуйста сказать, чего такого нет в WL, но есть в Julia?
Ну то есть простой пример на Julia, а я постараюсь ответить - есть ли подобное в WL.


vandalv
Спасибо за статью. Есть ли реализации символьного программирования в других популярных языках Java, c++, c# в виде библиотек?
Naf2000
В .net есть Expression, позволяющие работать с деревьями выражений. Например https://habr.com/ru/articles/149630/