Размышления о способах непрерывного обхода двухмерных массивов, в которых траектория не пересекает саму себя, привели к выводу что их и не так-то много. На самом деле простые алгоритмы (рациональные, с минимальным количеством поворотов) можно, как говорится, пересчитать по пальцам одной руки. Наиболее известные из них: обход по спирали и обход «змейкой». В сети можно найти предостаточное количество решений, основная часть которых опирается на фундаментальные элементы программирования: условные переходы и циклы.

Однако, некоторое время назад меня посетила шальная мысль: а нельзя ли придумать математическую формулу, которая могла бы вычислить значение любого элемента подобных матриц на основании лишь его координат? Такая формула, конечно, не ускорила бы процесс полного обхода матрицы и соответственно установления каких-либо значений по пути следования (обычно по возрастающей). Но она позволила бы узнать значение любого элемента независимо от его положения за одну операцию, без необходимости прохождения через предыдущие ячейки со счётчиком. Конечно, практическая значимость такой формулы остается под большим вопросом, однако сама по себе идея была заманчива и пробуждала спортивный интерес.

В результате на Хабре появились две работы (для спиральной матрицы — Альтернативный способ заполнения «спиральной матрицы», для матрицы «змейкой» — Математическое решение задачи о матрице «змейкой»), в которых достаточно подробно описаны формулы нахождения значений элементов матриц и методика их построения.

Непродолжительное время назад мне вспомнился еще один алгоритм обхода - т.н. «угловой обход».  Естественным образом возникло желание вывести уравнение и для этого способа, дабы обеспечить полноту коллекции формул для матриц широко известным числом 3. Следует отметить, что речь идет исключительно о квадратных матрицах, в которых количество столбцов равняется количеству строк.

Угловой обход и заполнение матрицы возрастающими значениями от 1 до N² показан на рисунке 1:

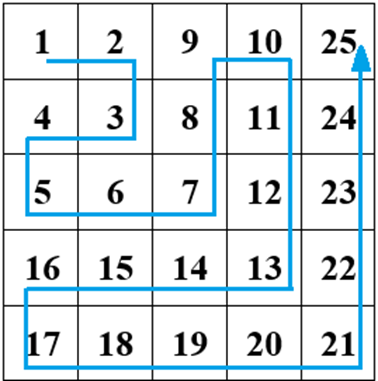
Полагается, что нет необходимости описывать на естественном языке изучаемую траекторию и приведённой схемы достаточно для уяснения ее сути. Остается лишь добавить, что вариантов углового обхода можно насчитать целых 8 штук, в зависимости от того, с какого угла и в каком направлении (по горизонтали или вертикали) начинается движение. Однако предстоящая работа связана с «традиционным» вхождением в массив с левого верхнего угла, с первым шагом по горизонтали. Результаты достаточно легко адаптировать для любого из других 7 способов.

Таким образом задача: построить математическое уравнение для вычисления значений элементов матрицы, не используя условные переходы и заранее заготовленные наборы данных: массивы, словари, множества и т.д. Циклы применяются только для перебора всех элементов массива и также не присутствуют непосредственно в уравнении. Аргументами выступают координаты заданной ячейки (I, J) и размер матрицы (N).

Подготовка. Математический аппарат будет строиться параллельно с разработкой кода на языке С++. Для обеспечения программной реализации решений подготовим соответствующий скрипт, объявив в нем массив размером 5x5 (присвоим ему оригинальное наименование «А») и заполнив его нулевыми значениями. Уравнение будет строиться и проверяться поэтапно в процессе его одновременной работы со всеми элементами матрицы, перебор которых производится традиционным способом двумя вложенными циклами от 1 до N.

Основной скрипт выглядит следующим образом:

#include <iostream>
using namespace std;
int main()
{
    int N = 5;          // задаем размер матрицы
    int a[N][N];        // и инициализируем ее
    for (int ik = 0; ik < N; ik++)
        for (int jk = 0; jk < N; jk++)
            a[ik][jk] = 0;          // заполнив для удобства нулями
                                      
    for (int ik = 0; ik < N; ik++){     //назовем его "Основной цикл"
        for (int jk = 0; jk < N; jk++){
        
            int i = ik + 1;     // Номера строк и столбцов приводим в удобный
            int j = jk + 1;     // в математическом плане вид (от 1 до N)  
            //  ... здесь будем вставлять основной код вычислений
     
        }   
    }     

   for (int ik = 0; ik < N; ik++){          //Блок "Вывод массива"
        for (int jk = 0; jk < N; jk++){
           printf( " %02d  " , a[ik][jk]);// дополняем число ведущими нулями
        }
        cout << endl;
    }  
    return 0;
}

1 этап. Как и в предыдущих случаях, задачу необходимо разделить на несколько этапов. На первом этапе предстоит разбить массив на секции, в которых элементы логически связаны друг с другом и представляют собой цельный интервал. В данном случае это угловые участки - полупериметры каждого вложенного квадрата матрицы (для прояснения столь запутанного предложения смотрим на рисунок 2).

Обозначив и пронумеровав каждую секцию на схеме, можно убедиться, что их количество равняется размеру матрицы.

Теперь же требуется вычислить номер секции по имеющимся аргументам, то есть координатам ячейки.

Как это сделать?

Для начала рассмотрим взаимосвязь координат ячеек с номерами секций на рисунке 3.

Отсюда видно, что номер секции, в которой находится элемент равняется наибольшему значению из двух чисел, обозначающих его координаты D = max (i, j). Но как определить наибольшее из двух чисел, не используя условный переход? К счастью, для этого имеется распространённый способ, заключающийся в делении суммы результата сложения и абсолютной разницы на 2. То есть по формуле max = ((a + b) + |a - b|) / 2. При этом, результат будет целочисленным, так как ((a + b) + |a - b|) всегда дает четное число.

В нашем случае, после ввода соответствующей переменной, это будет:

Не откладывая в долгий ящик, сразу пробуем это в компиляторе (результат на рисунке 4):

int D = (i + j + abs(i - j))/2;
a[ik][jk] = D;

Убедившись, что все прекрасно работает, переходим к следующему этапу.

2 этап. Теперь необходимо определить диапазон значений в каждой секции и расположить эти самые значения в возрастающем порядке хотя бы в одном направлении.

Учитывая, что работа осуществляется с абсолютно квадратной матрицей (неабсолютно квадратные матрицы – это прямоугольные матрицы, у которых количество строк не равняется количеству столбцов ????), становится очевидным, что максимальное значение в каждой секции равняется квадрату ее номера.

Выведем на экран массив с максимальными значениями в секциях (рисунок 5):

int M = D * D;
a[ik][jk] = M;

Далее, требуется выявить еще одну закономерность в самих координатах элементов, с помощью которой можно получить убывающий/возрастающий (естественно, на единицу) порядок значений в секциях. Для этого, вернемся к рисунку 3, и снова проанализируем его.

Сумма координат (i + j) явно не подходит, так как в результате мы получим возрастающий только до центрального элемента ряд. В дальнейшем он будет убывать.

Тогда следует попробовать разницу координат. Пусть для начала это будет i – j (рисунок 6).

a[ik][jk] = i  -  j;

Как видим, в направлении вниз и влево у нас отмечается стабильный рост экономики значений. Здесь же можем скорректировать секции так, чтобы они начинались не с отрицательных значений а с нуля. Для этого необходимо прибавить к каждому элементу номер его секции и вычесть единицу. Введем еще одну переменную и присвоим ей указанное выражение.

Реализуем это в компиляторе (рисунок 7):

int K = i  -  j + D - 1;
a[ik][jk] = K;

Следующий шаг очевиден - мы будем просто вычитать из максимальных значений указанные числа (и помещать результат в переменную R), т.е.:

Сразу проверяем в компиляторе (рисунок 8):

int R = M - K;
a[ik][jk] = R;

Таким образом мы наполовину решили проблему и получили необходимые значения в каждой секции. Однако их рост осуществляется только в правом и верхнем направлении.

3 этап. На последнем этапе необходимо добиться чередования направлении роста благосостояния населения значений в каждой секции.

Для начала получим обратный порядок элементов (тот самый отрицательный рост ????). Делается это с помощью замены «i – j» на «j – i» в предпоследней формуле (в уравнении 3).

Компилим и получаем зеркальный результат (рисунок 9):

int K = j  -  i + D - 1;
int R = M - K;
a[ik][jk] = R;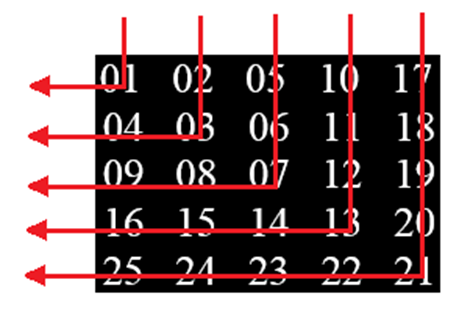

Непосредственно чередование получаем путем ввода некоего переключателя, который в зависимости от четности/нечетности номера секции будет использовать «i – j» или «j – i». Для этого введем еще одну переменную S (switcher) и присвоим ей значение:

S будет принимать значение 1 на нечетных и 0 на четных секциях. В свою очередь 1 – S поведет себя с точностью до наоборот. Нам понадобятся оба выражения.

Теперь расширим уравнение с участием переменной «К» следующим образом:

Здесь в зависимости от четности/нечетности секции активным становится «i – j» или «j – i». Тем самым обеспечивается чередование направлений роста. 

Пишем этот последний (или для некоторых – «крайний») шаг на С++ и смотрим на результаты (рисунок 10):

int S = D % 2;
int K = ( (i - j) * S  + (j -  i ) * (1 - S)  + D - 1);
int R =  D * D - K;
a[ik][jk] = R;

Как видим, шалость удалась!

Оформление. Остается только формальная часть – собрать все выражения и формулы в одном месте, удалить ненужные переменные, а также подготовить оконченный программный код.

Программный код для этих вычислений будет выглядит следующим образом:

int D = (i + j + abs(i - j)) / 2;
int S = D % 2;
int K = S * (i - j) + (1 - S) * (j - i) + D - 1;
int R = D * D - K;
a[ik][jk] = R;

Имея на руках этот рабочий алгоритм, можно бы и остановиться. Тем более, дальнейший анализ и различные математические извращения операции не привели к каким-либо значительным сокращениям (в плане реального уменьшения количества вычислительных шагов). Однако, все же удалось найти более компактный способ записи вычислений, а также выстроить уравнение без промежуточных переменных.

В первом случае достаточно избавиться от переменной «К», заменив ее полным выражением:

         Далее можно сократить его, раскрыв скобки, инвертировав знаки и логически сгруппировав элементы:

Программный код:

int D = (i + j + abs(i - j)) / 2;
int S = D % 2;
int R = D * D - D - (i - j) * (2 * S - 1) + 1;
a[ik][jk] = R;

Данный вариант (и математическое выражение и скрипт) представляется наиболее оптимальным, сбалансированным и удобочитаемым.

Однако, как было заявлено ранее, попытаемся построить выражение и код без каких-либо промежуточных переменных (как если бы программисту сокращали зарплату за каждую лишнюю переменную).

Однако, если говорить исключительно о сокращении способа записи, то следует избавиться и от «D²», чтобы сделать уравнение более однородным. Тем самым, упростится и программный код, избавляя нас от вечной проблемы выбора между повторением выражения (x * x) и использованием внешней функции (pow(x, 2)).

Наиболее перспективным для этой задачи выглядит многочлен «D² – D + 1», который можно разложить на множители при определенных условиях. Вспоминая курс школьной математики, отметим, что уравнение D² – D + 1 = 0 не имеет корней, и, соответственно его разложение прямым способом неосуществимо. В таком случае, выражение стоит записать в виде D² – D - 2 + 3, и разложить D² – D – 2 на целочисленные множители (D - 2) и (D + 1). В итоге получаем:

Такое преобразование обошлось в небольшое увеличение формулы на «+3».

Далее осталось только заменить «S» на «D mod 2»:

Теперь подставляем вместо всех «D» его начальное выражение, а «+3» отправим в конец уравнения:

Но и это еще не конец. Небольшой анализ говорит о возможности совершенствования формулы.

Во-первых, следует привести к общему знаменателю первые два дробные выражения в скобках:

Во-вторых, можно полностью сократить дробную часть в скобках, которые содержат деление с остатком (взятие остатка):

В результате получаем итоговое уравнение, состоящее исключительно из первичных переменных:

Скрипт:

a[ik][jk] = ((i + j + abs (i - j) - 4) / 2) * ((i + j + abs (i - j) + 2) / 2) 
                    - (i - j) * ((i + j + abs(i - j)) % 4 - 1) + 3;

Таким образом, все вычисления возможно записать одним уравнением и однострочным скриптом.

Итоги. Как и в предыдущих статьях, следует сделать небольшое заключение касательно проделанной работы. Несомненно, она является самой простой из всех трех, ввиду одной особенности: в качестве аргументов требуются только координаты элемента, а размер матрицы не нужен. Также необходимо отметить, что работа носит исключительно развлекательно-познавательный характер и не претендует на первенство или практическую применимость.