9 Синтез и коррекция систем автоматического регулирования (САР) / forpes.ru

Главная
9 Синтез и коррекция систем автоматического регулирования (САР)

9 Синтез и коррекция систем автоматического регулирования (САР)

17.03.2024 21:10

petuhoff 0 1500 Источник

Продолжаем публикацию лекций по предмету "Управление в Технических устройствах" Автор Олега Степановича Козлова. Кафедра "Ядерные энергетические установки" МГТУ им. Н.Э. Баумана. В предыдущих сериях:

1. Введение в теорию автоматического управления.2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.

3. Частотные характеристики звеньев и систем автоматического управления регулирования. 3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.

4. Структурные преобразования систем автоматического регулирования.

5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).

6. Устойчивость систем автоматического регулирования. 6.1 Понятие об устойчивости САР. Теорема Ляпунова. 6.2 Необходимые условия устойчивости линейных и линеаризованных САР. 6.3 Алгебраический критерий устойчивости Гурвица. 6.4 Частотный критерий устойчивости Михайлова. 6.5 Критерий Найквиста.

7. Точность систем автоматического управления. Часть 1 и Часть 2

8. Качество переходного процесса Часть 1 и Часть 2

9.1 Понятия о синтезе и коррекции САР

Проектирование САР (регулятор, усилители, вычислительные и логические устройства) направлено на создание такой системы уравнения, которая обеспечивает наилучшие характеристики качества уравнений (например, высокая точность и быстродействие, малое перерегулирование, хороший запас по фазе и амплитуде и т.д.). Почти всегда попытка достичь «лучших из лучших» качеств входит в противоречие, например:

Стремление обеспечить малые постоянные и скоростные очистки требует увеличения общего коэффициента усиления разомкнутой САР (К), а с другой стороны известно, что увеличение К уменьшает (в общем случае) запасы по фазе и амплитуде (вплоть до потери устойчивости), что отрицательным образом влияет на качество переходного процесса, а именно, увеличивает перерегулирование ( $\delta$ ) колебательность ( $\varphi$ );
Стремление повысить точность за счет повышения порядка астатизьма входи в противоречие с запасом устойчивости.

Поэтому проектирование «наилучшей» САР –задача из разряда оптимизационных.

В целом, процесс проектирования состоит из 3-х составных частей:

Анализа САР, проведение которого позволяет выявить общие закономерности поведения САР и ее динамических характеристик (анализ устойчивости, точности, качества проходного процесса и т.д.);
Синтеза САР, проведение которого позволяет «подобрать» для САР «наилучшее» корректирующее звено;
Коррекция САР, при которой «подобранное» при синтезе звена (корректирующее звено)вносится в структуру.

Анализа САР, проведение которого позволяет выявить общие закономерности поведения САР и ее динамических характеристик (анализ устойчивости, точности, качества проходного процесса и т.д.);Синтеза САР, проведение которого позволяет «подобрать» для САР «наилучшее» корректирующее звено;Коррекция САР, при которой «подобранное» при синтезе звена (корректирующее звено)вносится в структуру.

Синтез и коррекция САР – один из основных вопросов управления технологическими системами.

Обеспечение устойчивой и качественной работы САР с помощью дополнительных устройств (в том числе и регуляторов) называется коррекцией, а само устройство корректирующим.

Существуют различные методы коррекции САР:

Введение дополнительных параллельных связей, в том числе и обратных связей;
Введение последовательных корректирующих устройств;
Введение параллельных корректирующих устройств.

В принципе, «введения параллельных корректирующих устройств» входит в понятие «введение дополнительных параллельных связей», поэтому в последнем методе коррекции принято рассматривать только сложные параллельные корректирующие устройства.

Рассмотрим варин коррекции:

Рисунок 9.1.1а Последовательное корректирущие устройство

Рисунок 9.1.1б Паралельное корректирующие устройство

Рисунок 9.1.1в Корректирующие устройство с обратной связь

9.2 Введение дополнительных обратных связей

9.2.1 Жесткая обратная связь

В ряде случаев при проектировании САР необходимо изменить структуру какого-то звена (или группы звеньев). Одним из простейших приемов, позволяющих изменить структуру (а заодно и параметры, такие как коэффициент усиления, постоянная времени) является введение жесткой обратной связи (ж.о.с.)

Обратная связь называется жесткой, если в цепи обратной связи расположены:

Идеальное усилительное звено $\Rightarrow W_{oc}(s)=K_{oc}$ ;
Апереудическое звено 1-го порядка $\Rightarrow W_{oc}(s)=\frac{K_{oc}}{T_{oc}+1}$ .

Наиболее часто под жесткой обратной связью понимают случай, когда $W_{oc}(s)=K_{oc}$ ;

Рассмотрим «последствия» жесткой обратной связи:

a) Корректируемое звено – идеальное усилительное:

Рисунок 9.2.2 Коррекция усилителя усилителем

Передаточная функция эквивалентная: $W_{экв}(s)=\frac{K}{(1\pm K\cdot K_{oc})}=K_{экв}$

Выводы:

Звено остается усилительным.
Если обратная связь отрицательна, то : $K_{экв}<K$ ;
Eсли обратная связь положительна, то:
- $K_{экв}>K$ , если $K\cdot K_{ос}<1$ ;
- $K_{экв}<0$ , если $K\cdot K_{оc}>1$ (т.е. эквивалентное звено «работает» как инвертор)

б) корректирующее звено - апериодическое звено 1-го порядка:

Рисунок 9.2.3 Коррекция апериодики усилителем

$W_{экв}(s)=\frac{K}{(T\cdot s+1)\cdot\left [1\pm\cfrac{K}{T\cdot s+1}\cdot K_{oc}\right]} \Rightarrow \\ \Rightarrow W_{экв}=\frac{K}{T\cdot s+1\pm K\cdot K_{oc}}=\frac{K/(1\pm K\cdot K_{oc})}{\cfrac{T}{1\pm K\cdot K_{ос}}}\cdot s+1=\frac{K_{экв}}{T_{экв}\cdot s+1}$

Где $K_{экв}=\frac{K}{1\pm K\cdot K_{ос}}$ ; $T_{экв}=\frac{T}{1\pm K\cdot K_{ос}};$

Выводы:

Звено после коррекции не изменило своей структуры (т.е. осталось апериодическим 1-го порядка), хотя обычно структура звена меняется.

Если обратная связь отрицательна, то: $K_{экв}<K; \ T_{экв}<T.$
Если обратная связь положительна, то:
- $K_{экв}>K; \ T_{экв}>T$ , если $K\cdot K_{ос}<1$ ;
- Звено стало неустойчивым апериодическим звеном 1-го порядка, если $K\cdot K_{ос}<1$ .

b) корректируемое звено - идеально интегрирующее

$W_{экв}=\frac{K}{T\cdot s\left[1\pm\cfrac{K}{T\cdot s}\cdot K_{oc}\right]}\Rightarrow W_{экв}=\frac{\cfrac{1}{K_{oc}}}{\cfrac{T}{K\cdot K_{oc}}\cdot s\pm 1}=\frac{K_{экв}}{T_{экв}\cdot s+1}$

где: $K_{экв}=\frac{1}{K_{oc}}; \ T_{экв}=\frac{T}{K\cdot K_{oc}};$

Выводы:

Структура звена изменилась ⟹ оно стало апериодическим 1-го порядка.
Если обратная связь положительна, то эквивалентное звено – неустойчивое;
Если обратная связь - отрицательна, то значения $K_{экв}$ и $T_{экв}$ определяются величиной $K_{oc}$ .

Общее резюме:

1. Отрицательная жесткая обратная связь уменьшает постоянную времени и коэффициент усиления. Последнее (уменьшение К) приводит к увеличению статистической (постоянной ошибки).

2.При положительной обратной связи постоянная времени и коэффициент усиления увеличивается, однако возрастает вероятность образование неустойчивых звеньев.

3.В общих случаях структура звена изменяется.

9.2.2 Гибкая обратная связь

Гибкой обратной связью называется такая обратная связь, при которой в цепи обратной связи проводится дифференцирование выходного сигнала:

где: $W_{oc}=\tau_{oc}\cdot s$ - идеальное дифференцирующие звено; $W_{ос}=\frac{\tau_{oc}\cdot s}{\tau_{oc}\cdot s+1}$ - инерционное дифференцирующие звено.

В некоторых более сложных случаях используются более сложные дифференцирующие звенья.

Рассмотрим примеры простейшей гибкой обратной связи ( $W_{oc}=\tau_{oc}\cdot s$ - идеально дифференцирующее звено):

А) корректируемое звено - идеально усилительное звено

Рисунок 9.2.6 Коррекция идеальным дифференциальным звеном

$W_{экв}(s)=\frac{K}{1\pm K\cdot T_{oc}\cdot s}=\frac{K_{экв}}{T_{экв}\cdot s+1};$

где: $K_{экв}= K$ ; $T_{экв}=K\cdot \tau_{oc}$ .

Выводы:
1. Структура звена изменилась $\Rightarrow$ оно стало апериодическим 1-го порядка;
2. Коэффициент усиления остался неизменным;

Б) корректируемое звено - апериодическое звено 1-го порядка.

Рисунок 9.2.7 Коррекция апереодического звена дифференциальным

$W_{экв}(s)=\frac{K}{T\cdot s \cdot \left [1\pm\cfrac{K}{T\cdot s}\cdot\tau_{ос}\cdot s \right ]}\Rightarrow W_{экв}=\frac{K}{(T\pm K\cdot \tau_{oc})\cdot s}=\frac{K_{экв}}{T_{экв}\cdot s}$

где: $K_{экв}=K, \ T_{экв}=T\pm K \cdot \tau_{oc}.$

Выводы:
1. Структура звена не изменилась.
2. Коэффициент усиления остался неизменным.
3. Если обратная связь отрицательна, то $T_{экв}>T$ ;
4. Если обратная связь положительна, то $T_{экв}<T$ , вплоть до создания инвертирующего интегрирующего звена.

Общее резюме:

1. Гибкая обратная связь не изменяет коэффициент усиления корректируемой части САР.

2. Гибкая обратная связь зачастую не изменяет структуру корректируемого звена.

3. Отрицательна гибкая обратная связь увеличивает постоянные времени; положительная гибкая обратная связь уменьшает постоянные времени.

4. Статическая характеристика корректируемого звена не изменяется (т.к. $K_{экв}=K$ ).

9.2.3 Смешанные обратные связи

В некоторых случаях обратная связь может одновременно обладать свойствами жесткой и гибкой обратной связи.

Примером такой связи может быть форсирующее звено: $W_{ос}(s)=K_{ос}\cdot (1+T_{ос}\cdot s)$ ,

или инерционно-форсирующие звено $W_{ос}(s)=\frac{K_{oc}\cdot(1+T_{оc}\cdot s)}{T_{oc}\cdot s+1}$ .

Принято называть такие связи смешанными.

Смешанные обратные связи изменяют параметры охватываемого звена (коэффициент усиления, постоянные времени), а также зачастую и его структуру, значительно усложняя ее.

С другой стороны, для целей стабилизации (устранения неустойчивости) эффект от использования смешанной связи может быть существенно больше, чем при жесткой обратной связи или гибкой обратной связи Полученное при такой коррекции эквивалентное звено имеет более высокий порядок, чем исходное звено.

Рисунок 9.2.9 Коррекция смешанными обратными связями

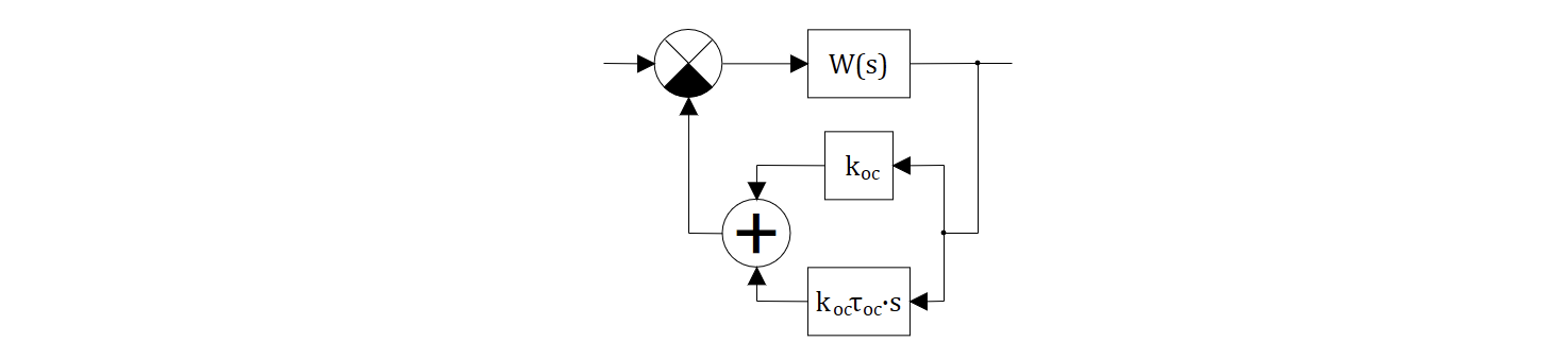
9.3 Введение производных в закон управления

Данный способ коррекции САР относится к типу «введение дополнительных параллельных связей», а именно: он реализуется при помощи прямых параллельных связей.

Наиболее наглядно достоинства (и недостатки тоже) данного способа коррекции можно проиллюстрировать следующим примером, см. рисунок 9.3.1:

Рисунок 9.3.1 Добавление производных в закон управления

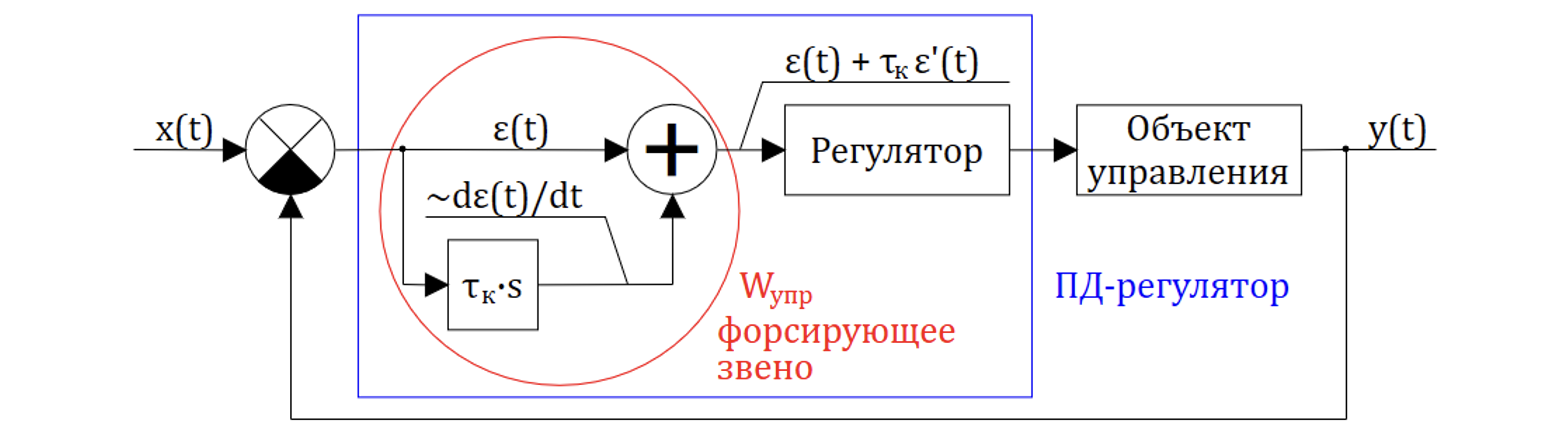
В данном примере исходная САР (черный цвет) осуществляла пропорциональное управление, т.е. входным (управляющим) сигналом на регулятор являлось рассогласование $\varepsilon(t)$ . С целью повышения быстродействия введена дополнительная параллельная связь, формирующая управляющий сигнал, пропорциональный производной от рассогласования - $d\varepsilon(t)/dt$ .

Рассмотрим на рисунке 9.3.2 последствия такой коррекции (в зависимости от t):

Рисунок 9.3.2 Коррекция введением дополнительных связей

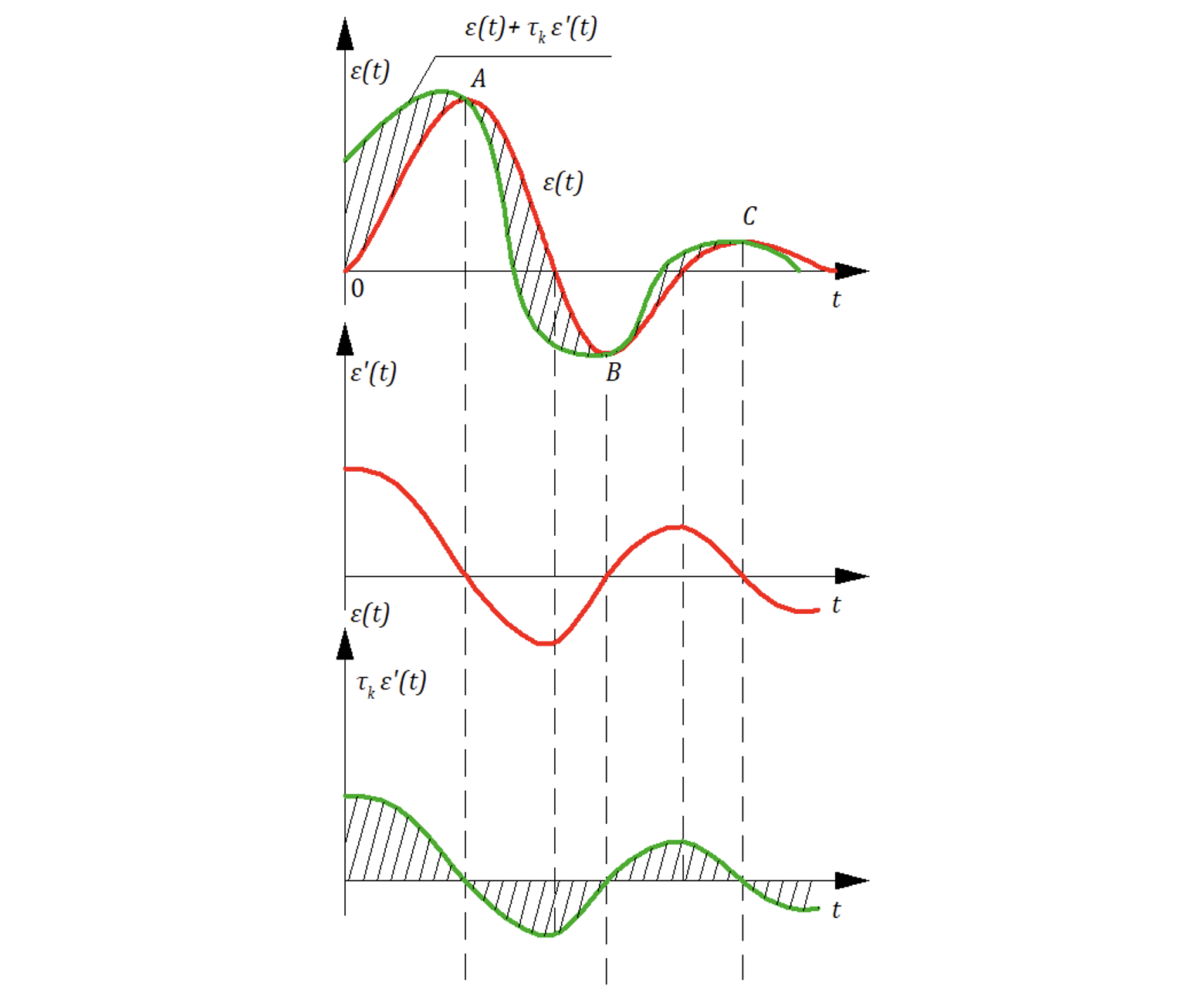
На участке ОА «сигналы» $\varepsilon(t)$ и $\varepsilon'(t)$ - одинаковых знаков, поэтому входной сигнал на регулятор больше, чем при чисто пропорциональном регулировании;

На участке АВ – наоборот, входной сигнал регулятора меньше, чем при чисто пропорциональном регулировании.

Резюме: введение производных в закон управления ускоряет действие регулятора на участке возрастания рассогласования $\varepsilon(t)$ и «тормозит» при уменьшении рассогласования.

Этим достигается увеличение быстродействия САР, т.к. происходит уменьшение времени переходного процесса.

Введение производных в виде дополнительной параллельной связи означает, что устройство управления «регулятором» имеет передаточную функцию, аналогичную форсирующему звену, $\Rightarrow$

$W_{упр}(s)=1+T_k\cdot s-1/(T_k\cdot s+1)$ - типичный вид передаточной функции форсирующего звена.

Регулятор (вместе с устройством управления – $W_{упр}$ ) реализует пропорцианально-дифферециальный закон управления, поэтому такой регулятор называют обычно ПД-регулятор (пропорционально-дифференциальный регулятор).

Наряду с достоинством такого способа коррекции (увеличение быстродействия), введение производных в закон управления имеет серьезный недостаток - увеличивается влияние высокочастотных помех.

К другим достоинствам рассматриваемого способа коррекции необходимо отнести:

Неизменность общего коэффициента усиления разомкнутой САР, что не ухудшает (и не улучшает) точность, в установившемся режиме;
Неизменность запасов устойчивости (по фазе и по амплитуде).

9.4 Введение интеграла в закон управления

Для повышения точности регулирования (как в установившемся режиме, так иногда и в динамическом) в структуру управляющего устройства вводят интегрирующие звенья, что означает введение в закон управления наряду с пропорциональным регулированием и «интеграла». Это означает, что параллельно с сигналом рассогласование проходит сигнал, пропорциональный интегралу от рассогласования.

Рассмотрим исходную САР, подобную рассмотренной ранее в подразделе 9.3 (см. рисунок 9.4.1 и сравните с рисунком 9.3.1).

Рисунок 9.4.1 Коррекция с интегратором в законе управления

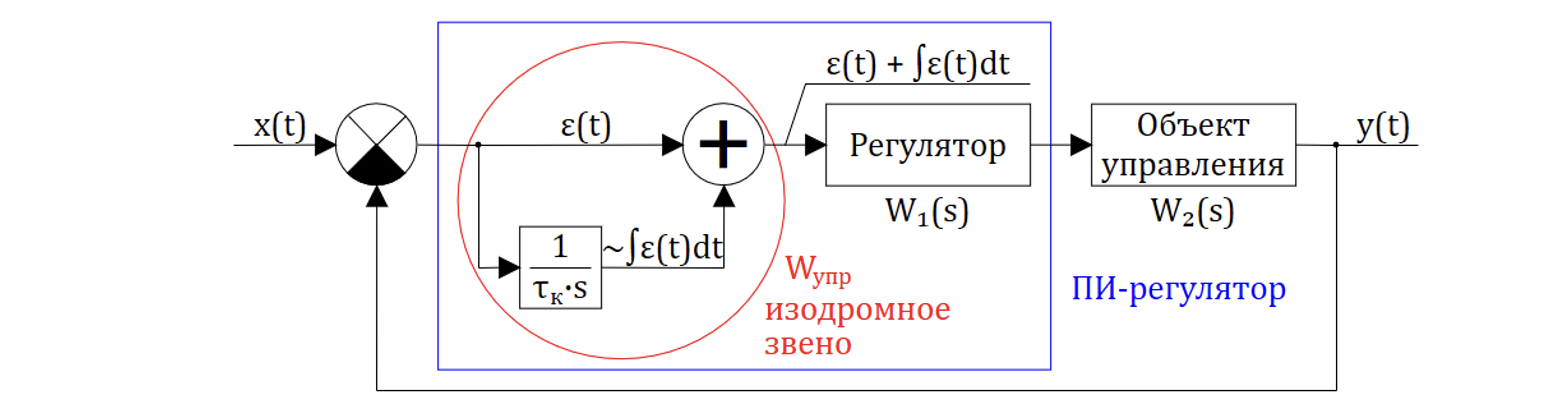
В данном примере сигнал управления, поступающий на вход регулятора, равен сумме отклонения и интеграла от отклонении:

$(\varepsilon(t)+\int_0^t\varepsilon(t)dt)$ ,

т.е. управление ведется не только пропорционально рассогласованию, но и пропорционально интегралу от рассогласования.

Данный метод коррекции повышает точность за счет увеличения астатизма САР (т.е. добавляется нулевой полюс разомкнутой САР), однако уменьшает (почти всегда) запасы устойчивости по фазе и амплитуде.

Покажем последнее анализом (сравнением) АФЧХ исходной и скорректированной САР:

$W_{исх}=W_1(s)\cdot W_2(s)\Rightarrow W_{исх}(i\cdot \omega)=W_1(i\cdot \omega)\cdot W_2(i\cdot \omega)$

Рисунок 9.4.2 Изменение годографа при интеграле в законе управления

$W_{экв}=W_{упр}(s)\cdot W_{исх}(i\cdot\omega)\Rightarrow W_{упр}=1+\frac{1}{\tau\cdot s}=\frac{\tau\cdot s+1}{\tau\cdot s}$

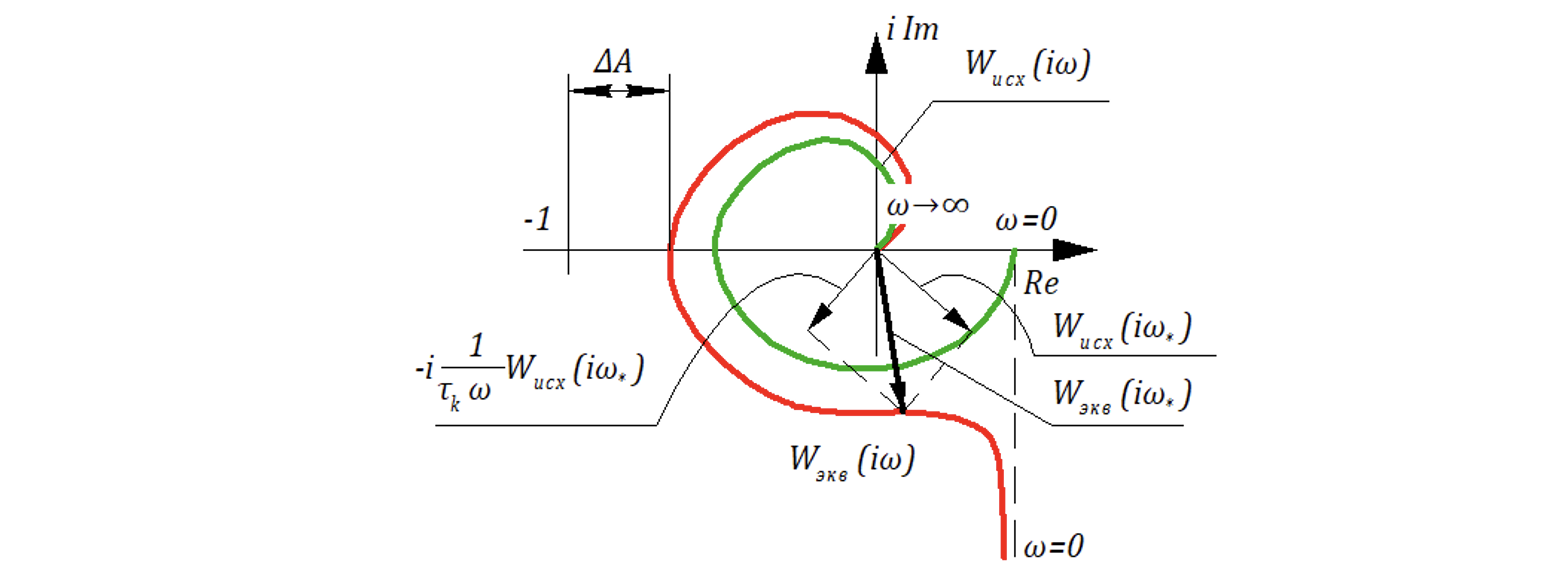
структура этого звена соответствует и заданному звену.

$W_{экв}(s)=W_{упр}\cdot W_{исх}\Rightarrow (1+\frac{1}{\tau\cdot s})\cdot W_{исх}\Rightarrow\\ \Rightarrow W_{экв}(i\cdot \omega)=W_{исх}(i\cdot\omega)+\frac{1}{i\cdot\varepsilon\cdot\omega}\cdot W_{исх}(i\cdot \omega) =\\ =W_{исх}(i\cdot\omega)-i\cdot \frac{1}{\tau\cdot \omega}\cdot W_{исх}(i\cdot \omega).$

Из рисунка следует, что введение интеграла в закон управления «добавляет» ко всем векторам АФЧХ исходной САР векторы, повернутые относительно $W_{исх}(i\cdot \omega)$ в отрицательном направление (по часовой стрелке) на угол в 90˚ и изменение в $1/(\tau\cdot \omega)$ раз. Это означает, что годограф АФЧХ скорректированной САР ( $W_{исх}(i\cdot \omega)$ ) пересечет ось абсцисс несколько левее, чем годограф исходной САР. Поэтому запас по амплитуде $\Delta A$ и запас по фазе $\Delta \varphi$ несколько уменьшается ⟹ это ухудшает качество переходного процесса. Но с другой стороны годограф скорректированной САР стал соответствовать годографу астатической САР, что несомненно повышает точность САР в установившемся режиме.

Регулятор (с управляющим устройством), который реализует управление пропорциональное как рассогласованию, так и интегралу от рассогласования, называется ПИ-регулятором (пропорционально-интегрирующий).

Если регулятор реализует одновременно пропорциональный, интегрирующий и дифференцирующий закон управления, такой регулятор называется ПИД-регулятором, см. рисунок 9.4.3.

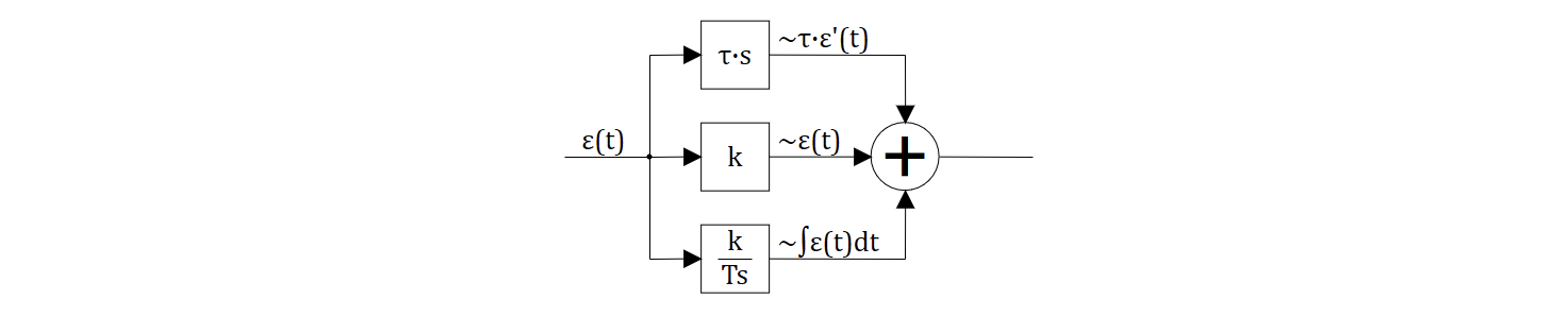
9.5 Полиномиальные корневые методы синтеза САУ

Подробное описание корневых методов описано в статье Леонида Марковича Скворцова в терех частей.

Предупреждение! Уровень статьи значительно выше начального студенческого!

Часть 1 смотри здесь... Часть 2 смотри здесь... Часть 3 смотри здесь...

9.6 Понятия о синтезе последовательных корректирующих устройств

Желаемого качества процесса управления (или регулирования), включающего требования точности запасов устойчивости, качества переходного процесса и т.д. можно достичь (обеспечить) 2-я способами:

1 способ: желаемого качества достигают путем изменения параметров (постоянных в решении, коэффициентов усиления) системы управления, поскольку при изменении параметров, соответственно, изменяются коэффициенты уравнения динамики САР и частотные характеристики САР;

2 способ: желаемое качество управления достигается за счет изменения структуры САР, а именно, за счет введения дополнительных звеньев - корректирующих устройств.

Наибольшее распространение коррекции за счет внесения дополнительных корректирующих устройств имеют последовательные корректирующие устройства.

Использование дополнительных корректирующих устройств и, особенно, последовательных корректирующих устройств позволяет не только сделать неустойчивую исходную САР устойчивой, но и придать скорректированной САР желаемое качество управления.

Принцип коррекции САР с помощью последовательного корректирующего устройство иллюстрируется следующим рисунком (9.5.1):

Рисунок 9.5.1 Последовательное корректирующие звено

корректирующее звено «вставляется» между главным сравнивающим устройством и неизменной частью (т.е. W(s)) исходной САР.

В широком смысле целями коррекции исходной САР могут быть:

Достижение требуемых запасов устойчивости;
Достижение (обеспечение) заданной точности, например, скоростной ошибки в установившемся режиме E_уст ;
Обеспечение допустимой (требуемой) величины перерегулирования $\delta$ , т.е. $\delta \le \delta_{доп}$ ;
Обеспечение требуемого времени переходного процесса $T_{пп}$ т.е. $T_{пп}\le T_{доп}$ ;
Обеспечение требуемой оценки интегральной оценки качества переходного процесса, т.е $Y\le Y_{доп}$ см. качество переходного процесса.

Очевидно, чем меньше установившиеся ошибки, меньше перерегулирование, меньше время переходного процесса и наоборот, чем больше запасы по фазе и амплитуде, тем качество САР – лучше.

Однако вышеприведенное не может быть реализовано одновременно в полной мере, поэтому задача определения структуры и параметров скорректированной САР (задача синтеза САР) сводится к оптимизационной задаче, т.е. последовательное корректирующее звено должно обеспечить скорректированной САР такие характеристики, которые «укладываются» в «поставленные допуски» по характеристикам.

Существует 2 подхода к решению задачи синтеза последовательного корректирующего устройства:

Графический, основанный на использовании логарифмических амплитудных и частотных характеристик разомкнутой (или замкнутой) САР;
Численный, основанный на методах параметрической оптимизации.

Графоаналитический метод синтеза последовательных корректирующих устройств, был очень распространен 20 40 лет назад, хотя и в настоящее время он не потерял своей актуальности (за счет относительной простоты расчетных процедур).

Использование графоаналитического (частотного) метода синтеза последовательного корректирующего устройства можно разделить на несколько этапов.

1 этап. Строится ЛАХ и ФЧХ исходной разомкнутой САР;

2 этап. На основании поставленных требований (по величинам ошибок, перерегулирования, времени переходного процесса и т.д.) строится логарифмическая амплитудная характеристика (ЛАХ) желаемой САР;

3 этап. Методом «графического вычитания» находится ЛАХ (и ФЧХ) корректирующего звена;

4 этап. Расчетным путем определяются параметры корректирующего звена (коэффициент усиления, постоянные времени);

5 этап. Проверка правильности выполненного синтеза последовательного корректирующего устройства путем построения переходного процесса при ступенчатом (в том числе и единичном) управляющем воздействии. Если синтез выполнен правильно, то требования, предъявленный к качеству, должны соблюдаться (выполняться).

Принципы и последовательность действий рассмотрим на следующем примере.

Пример:

Исходная САР, замкнутая единичной обратной связью, имеет передаточную функцию разомкнутой системы.

$W(s)=\frac{K}{s\cdot(T_1\cdot s+1)\cdot(T_2\cdot s+1)}$

где: $K =50 \ c^{-1}; \ T_1=0.01 \ c; \ T_2 = 0.05 \ c$ .

Найти структуру и параметры последовательно- корректирующего звена, обеспечивающего следующие требования к САР в замкнутом состоянии:

Максимальное перерегулирование не должно превышать 20% ( $\delta\le0.2$ );
Время переходного процесса не более 0.8 сек. (по входу в 5-й % трубку), $T_{ПП}\le 0.8 \ c$ ;
При подаче линейного управляющего воздействия $x(t)= a\cdot t$ установившаяся ошибка не должна превышать $0.005\cdot a$ , т.е. $\varepsilon_{уст}\le 0.005 \cdot a$ .

Рисунок 9.5.2 Схема корекции последовательным звеном

Раскроем скобки в передаточной функции и воспользуемся блоком «Передаточная функция общего вида» SimInTech для создания модели САР:

$\frac{k}{(T_1\cdot s+1)\cdot s\cdot (T_2\cdot s+1)}=\frac{k}{T_1\cdot T_2\cdot s^3+(T_1+T_2)\cdot s^2+s}$

C учетом численных значение исходная передаточная функция будет выглядеть как показано на рисунке 9.5.3

Рисунок 9.5.3 Исходная САР в среде SimInTech

Согласно условию задачи, система должна быть астатической с установившейся линейной ошибкой $\varepsilon_{уст}\le0.005$ . Поскольку установившая сошибка связанная для астатического звена расчитывается по формуле $\varepsilon_{уст}=a/k$ (cм. лекуцию 7. Точность систем автоматического регулирования (ч.1)) получаем:

$0.005\cdot a\le\frac{a}{k}\Rightarrow k\ge\frac{1}{0.005}\le 200$

Таким образом для минимального коэффициента усиления скоректировнного звена будет значение 200. 50 у нас в исходной сам, поэтому добавим в модель коэффициент усиления 4, что бы получить требуемую добортность системы. Скореектированная САР в первом приближении предсталенна на рисунке 9.5.4

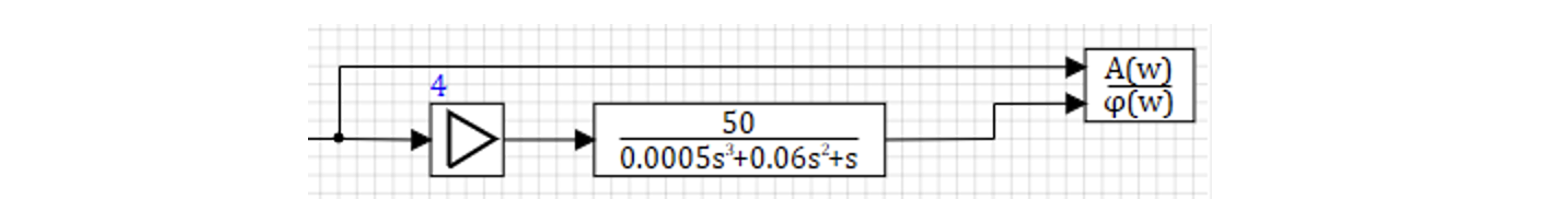
C помощью блока Построение частотных характеристик построим ЛАХ и ФЧХ и оценим усточивость с помощью критери Найквиста.

Рисунок 9.5.5 ЛАХ и ФЧХ скоректированного звеа

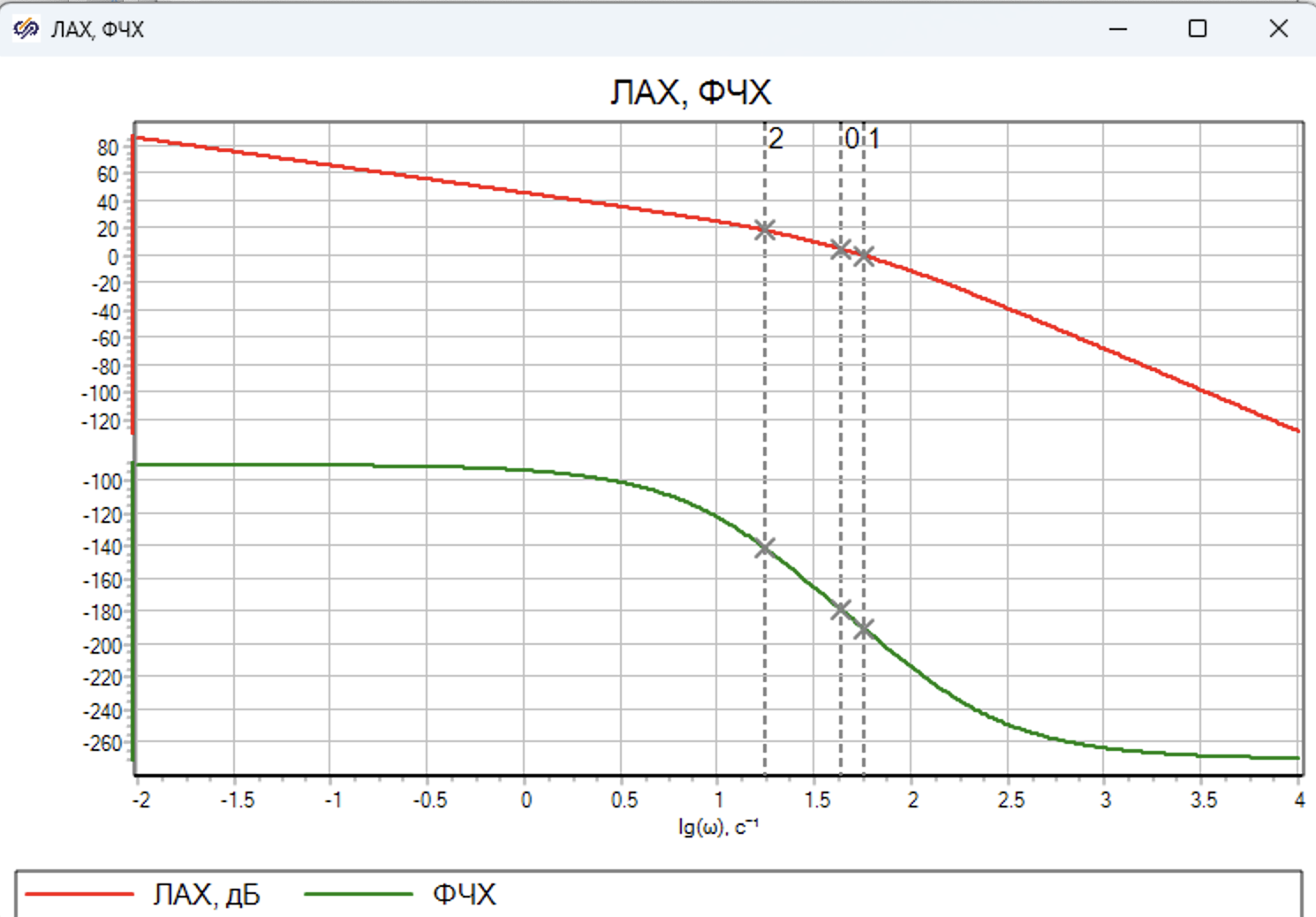
"Необходимым необходимым и достаточным условием устойчивости замкнутой САР является требование чтобы частота среза $\omega_{ср}$ (т.е. частота, при которой $A(\omega_{ср}) =1$ , а логарифм единичной амплитуды равен $Lm(\omega_{ср}) =0$ лежала левее частоты, при которой сдвиг фазы $\varphi(\omega)=-\pi$ . (см. лекцию критерий устойчивости Найквиста)

Из рис. 9.5.5 следует, что полученная САР неустойчива частота среза (курсор 1, см. рис. 9.5.5), лежит правее частоты сдвига фазы -180 (курсор 0, см. рис. 9.5.5). Для получения запаса устойчивости, например для запас по фазе $\Delta Y\approx 40^ \circ$ частота среза должна лежать в точке где $lg(\omega)\approx 1.3$ (курсор 2, см. рис. 9.5.5)

Создадим замкнутую модель, со ступенчатым воздействием и проверим результат воздействия:

Рисунок 9.5.6 Замкнутая САР и ступенчатое воздействие

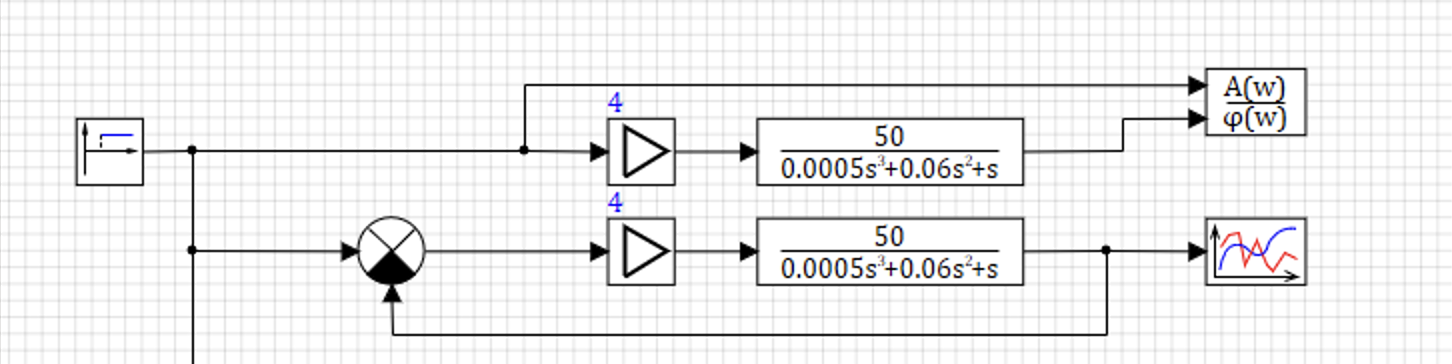
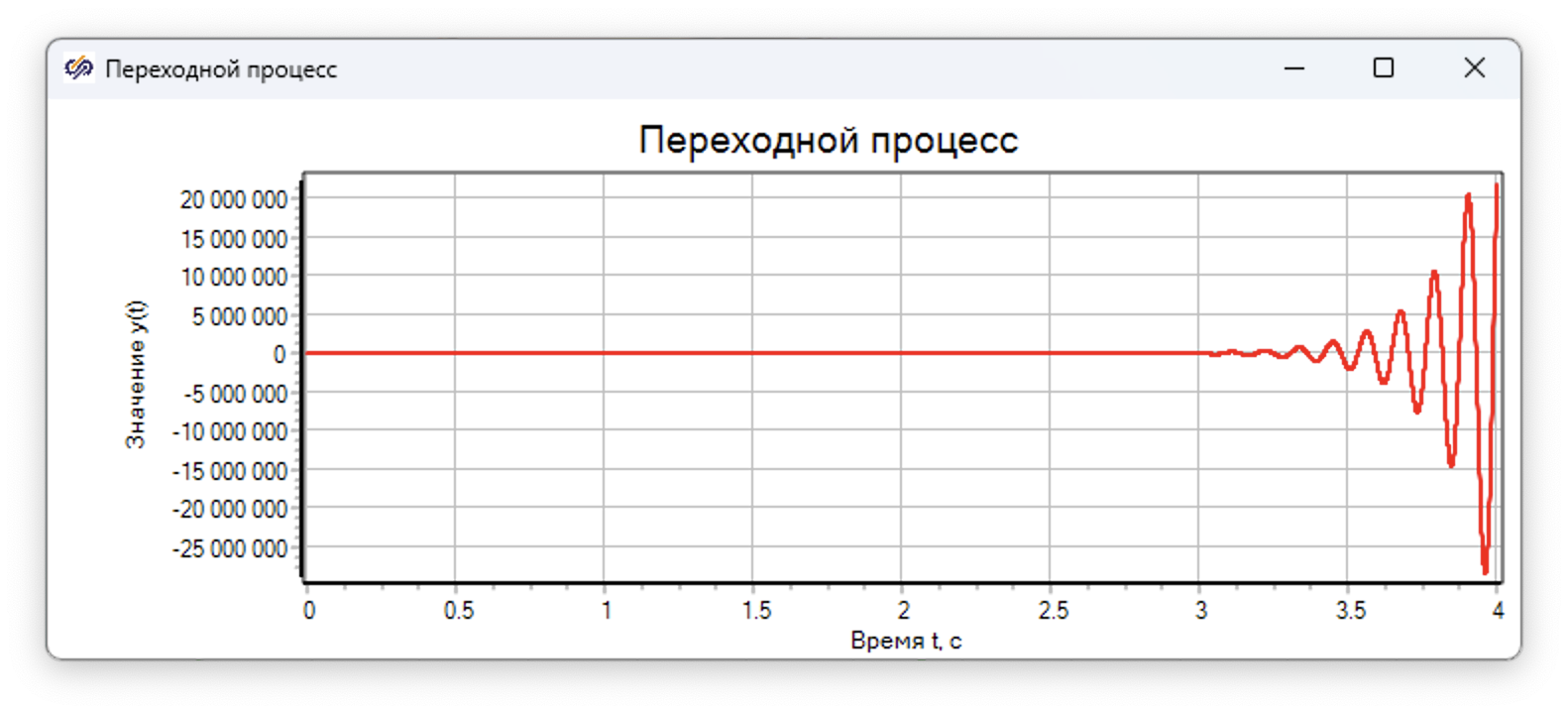
Переходной процесс при ступенчатом воздействии представлен на рисунке 9.5.6:

Рисунок 9.5.7 Переходной процесс замкнутой в первом приближении САР

Воспользуемя графиком на рисунке 9.5.5 и определим точку на оси $lg(\omega)$ , для частоты среза, такую что бы запас усточивости по фазе был $\Delta Y \approx 40 ^\circ$ это точка где $lg(\omega)\approx 1.3$

Далее обратимся к графику существующий ЛАХ и построим желательную характеристику см. рисунок 9.5.8

Рисунок 9.5.8 Графическое построение желательной ЛАХ

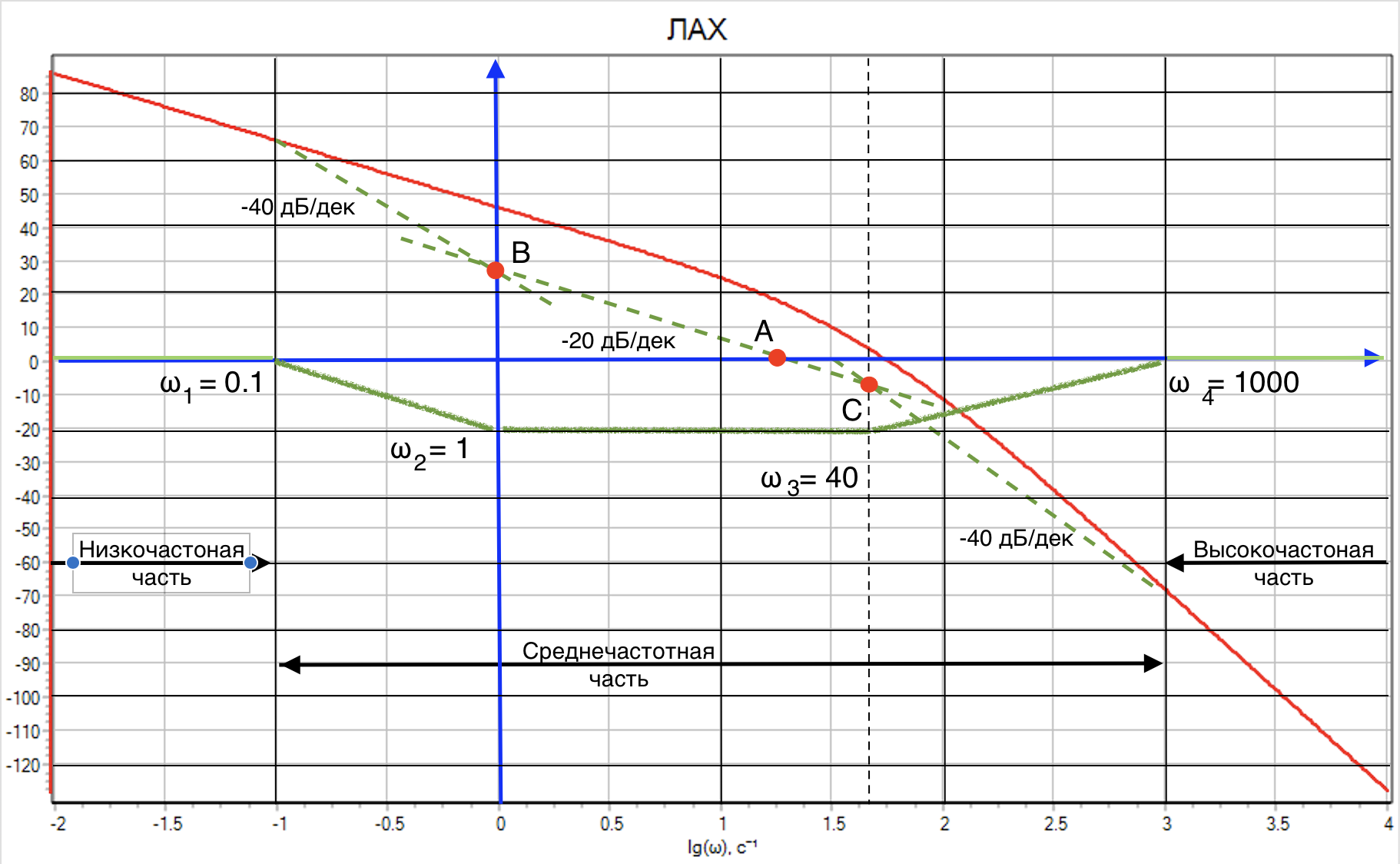
Для обеспечения наилучшей переходной характеристики желательно, что бы наклон ЛАХ в области частоты среза составлял -20 дБ/дек (см. Апереодическое звено 1-го порядка) Проведем линию через точку А желательной частоты среза с наклоном -20 дБ/дек

В низкочастотной области $\omega_1<0.1 \ (lg(\omega)<-1)$ оставим угол наклона без изменений ЛАХ -20 дБ/дек. После частоты $\omega_1$ проведем линию с наклоном -40 дБ/дек, определим место пересечения между линией - 20 дБ/дек, проведенной через желательную частосту среза линией - 40 дБ/дек. Это точка B, ей соответсвуует частота $\omega_2=1$

В высокочастотной области оставим $\omega_4>1000$ ( $lg(\omega)>3$ ) угол наклона ЛАХ без изменений - 60 дБ/дек. Из точки $\omega_4$ частоты проведем линию с наклоном -40 дБ/дек в сторону частоты среза и найдем точку пересечение с линей -20 дБ/дек проведенной через желательную точку среза, получим точку С, ей соответсвует частота $\omega_3\approx40$

Таким образом мы молучили желательную ЛАХ, для нашей САР в среднечатотной части. На рисунке 9.5.8 зеленая пунктирная линия. После этого осуществляем графическое вычитание существующий ЛАХ и желательный (помним что при перемножении лографмы складываются) и получам примерную ЛАХ желательного коректирующего звена (зеленая сплошная линия на рисунке 9.5.8).

Такую ЛАХ можно получит последовательным переложением апереодического звена 1-го порядка (- 20 дБ/дек) (начальный прямой участок и наклон второго участька ЛАХ), форсирующего звена (+20 dB/дек) (выпрямление третье участка ЛАХ), форсирующего звена (+20 дБ/дек) (подьем четвертого участка), апериодического звена первого порядка (-20 дБ/дек) (выпрямление 5-го участка). При этом частоты перегиба для каждого звена соответвуют полученным графически. Тогда общее передаточное коректирующее звено будет выглядеть так:

$W_{кор}= \frac{1}{(\cfrac{1}{\omega_1}\cdot s+1)}\cdot({\cfrac{1}{\omega_2}+1)}\cdot(\frac{1}{\omega_3}+1)\cdot\frac{1}{\cfrac{1}{\omega_4}+1} =\\ =\frac{T_2\cdot s+1}{T_1\cdot s+1}\cdot\frac{T_3\cdot s+1}{T_4\cdot s+1}$

где: $T_1=\frac{1}{\omega_1} =10$ ; $T_2 =\frac{1}{\omega_2}=1;$ $T_3=\frac{1}{\omega_3}\approx 0.025$ ; $T_4=\frac{1}{\omega_4}=0.001.$

Введем коректирующее передаточную фукнцию в модели, и проведем моделирование, модель представлена на рисунке 9.5.9 Результаты моделированя на рисунке 9.5.10

Рисунок 9.5.10 Переходной процесс скоректированной САР

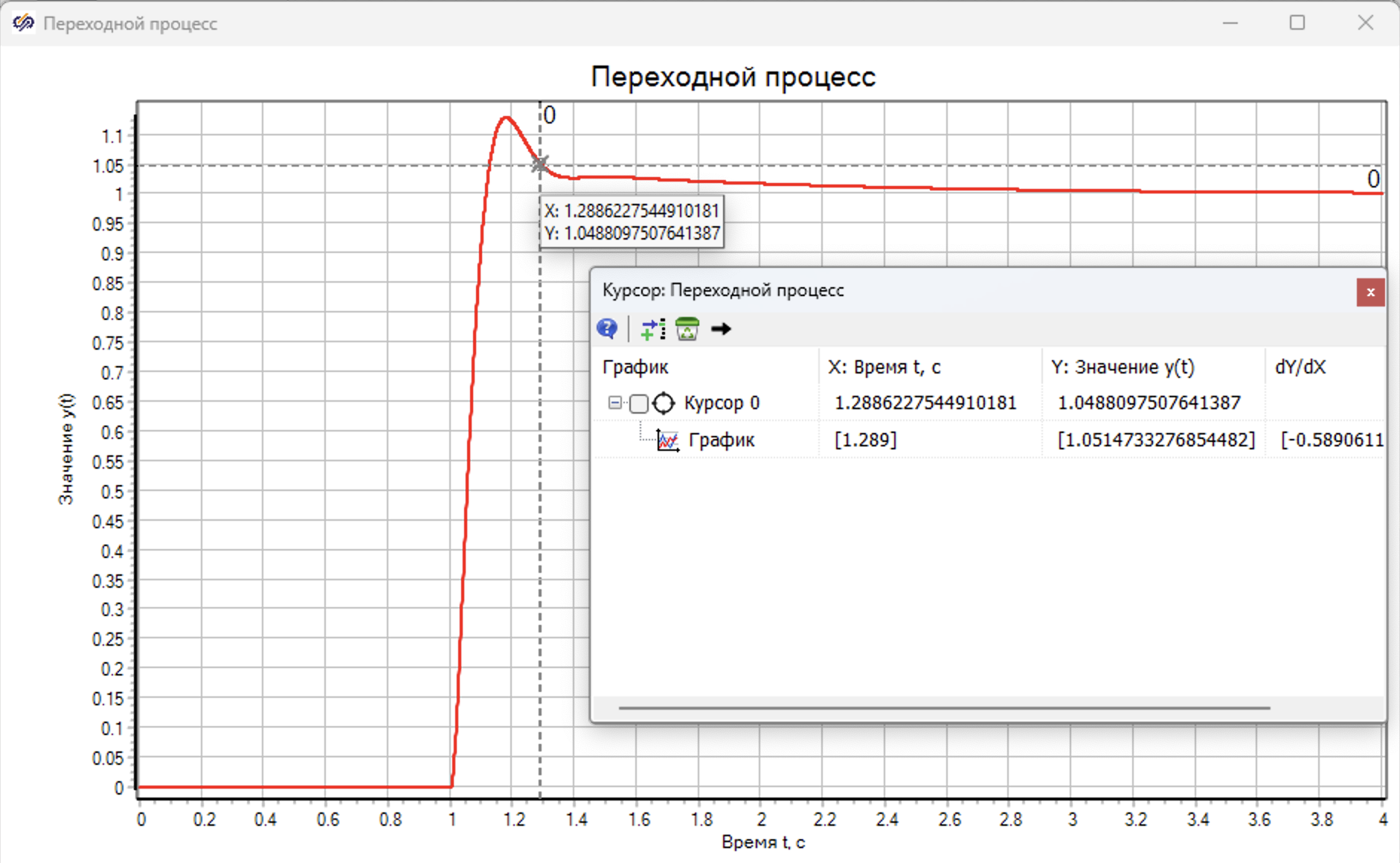
По результатм видно, что все требвания к системе (перерегулирование, время переходного процесса) выполнены.

Лично для меня такие результаты полученные с помощью миллиметровки линейки диаграмм всегда поражали. Без компьютера, только карандашом и линейкой можно синтезировать САР это очень круто я считаю.

В качестве бонуса небольшое видео. Сравиниваем дедовский графический способ коррекции САР из лекции и современный способ методом параметрической оптимизации. Результаты вас удивят. По крайне мере меня удивил. Получили лишнее подтверждение моего недоумения ранее опубликованого в статье "Почему падают темпы прогресса?"

Модели из лекции и показанные в видео можно взять здесь...