Когда я первый раз столкнулся с темой бинарных деревьев в программировании, то сразу нашел на Хабре ответы почти на все возникшие у меня вопросы, но время шло, вопросов становилось больше и совсем недавно я нашел тему, которую еще не осветили на данном ресурсе — это 2-3-4 деревья. Есть отличная статья на тему 2-3 деревьев, в которой можно найти ответы на вопросы «Что такое куча?», «Что такое 2-3 деревья», а также информацию про основные операции со структурой, поэтому я не буду повторяться и сразу перейду к главной теме.

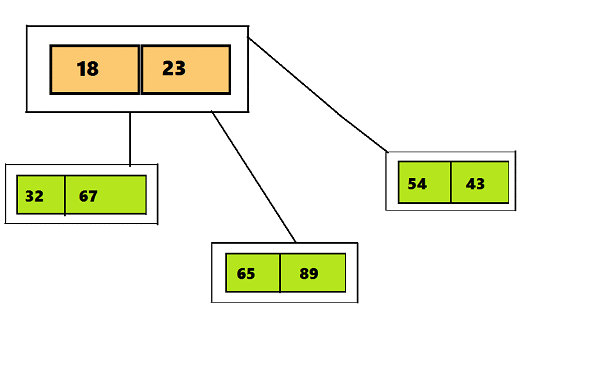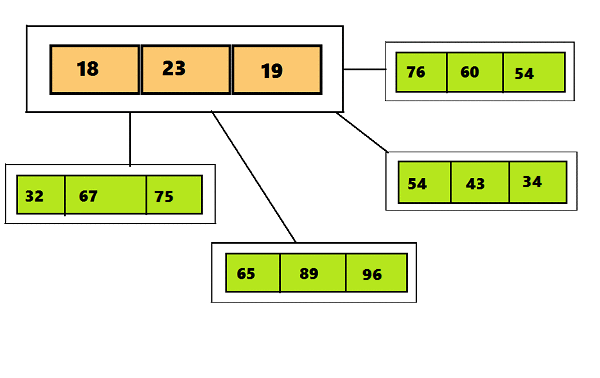
Итак, главное отличие 2-3-4 деревьев от 2-3 состоит в том, что они могут содержать более трех дочерних узлов, что дает возможность создавать четырехместные узлы (узлы, имеющие четыре дочерних узла и три элемента данных). Можно увидеть отличия визуально на гифке под эти текстом.На первом слайде показано 2-3 дерево, на втором — 2-3-4.



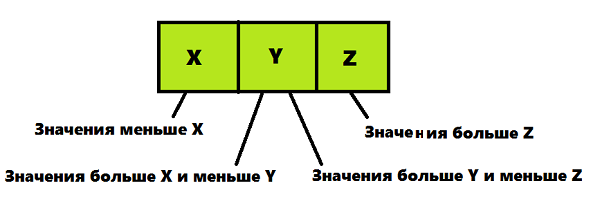
К данным, размещаемым в узлах 2-3-4 дерева выдвигаются некоторые требования (как и к данным, которые размещаются в 2-3 деревьях) — короткое изображение данной информации вы можете увидеть на картинке под текстом:

1. Если узел содержит 2 элемента и имеет 2 дочерних узла, то узел должен содержать один элемент, значение которого должно быть больше, чем значения левого дочернего узла, и меньше, чем значения правого дочернего узла
2. Если узел содержит 2 элемента и имеет 3 дочерних узла, то узел должен удовлетворять следующим соотношениям: значение X больше значений левого дочернего узла и меньше значений среднего дочернего узла; значение Z больше значений среднего дочернего узла и меньше значений правого дочернего узла.
3. Если узел содержит 3 элемента и имеет 4 дочерних узла, то узел должен удовлетворять следующим соотношениям: значение X больше значений левого дочернего узла и меньше значений левого среднего дочернего узла; значение Y больше значений левого среднего дочернего узла и меньше значений правого среднего дочернего узла; значение Z больше значений правого среднего дочернего узла и меньше значений правого дочернего узла.
4. Лист может содержать один, два или три элемента.

Главные плюсы 2-3-4 деревьев в сравнении с 2-3 деревьями состоят в том, что стандартные операции вставки и удаления элементов осуществляются за меньшее количество шагов. Главным минусом является количество требуемой памяти, ведь по скольку 2-3-4 деревья могут содержать большее количество элементов, которые потребуется где-то хранить, надо будет потреблять больше памяти. Для того что-бы устранить эту проблему можно использовать красно-черное бинарное дерево (red-black tree) специального вида, но про них мы поговорим позже.

Перед тем как описать принципы основных операций 2-3-4 деревьев, я наведу пример кода из книги «Абстракция данных и решение задач на C++», как можно классом описать 2-3-4 дерево.

сlass TreeNode
{
private:
TreeltemType smallltem, middleltem, largeltem;

TreeNode *leftChildPtr, *lMidChildPtr,
*rMidChildPtr, *rightChildPtr;

friend class TwoThreeFourTree;
};

Поиск в 2-3-4 дереве

Алгоритм поиска в элементах 2-3-4 дерева схож с алгоритмом поиска в элементах 2-3 дерева (эффективность алгоритма поиска
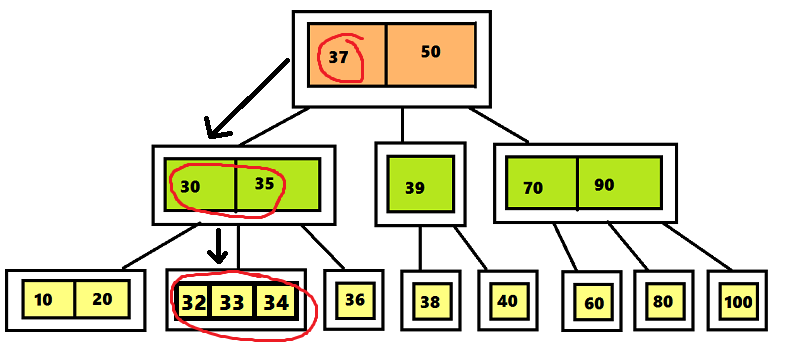
в 2-3 дереве имеет порядок O(log n)), можно сказать, что алгоритм тот же, но он расширен. Суть заключается в том, что например для поиска в дереве элемента, содержащего значение 31, хорошо было бы обследовать левое поддерево корня, поскольку число 31 меньше, чем 37. Затем обследуется среднее поддерево узла <30 35>, поскольку число 31 лежит между 30 и 35. Поиск заканчивается указателем на левый дочерний узел узла <32 33 34>, поскольку число 31 меньше, чем 32. В результате приходим к выводу, что в дереве нет элемента, содержащего значение 31.

Вставка в 2-3-4 дерево

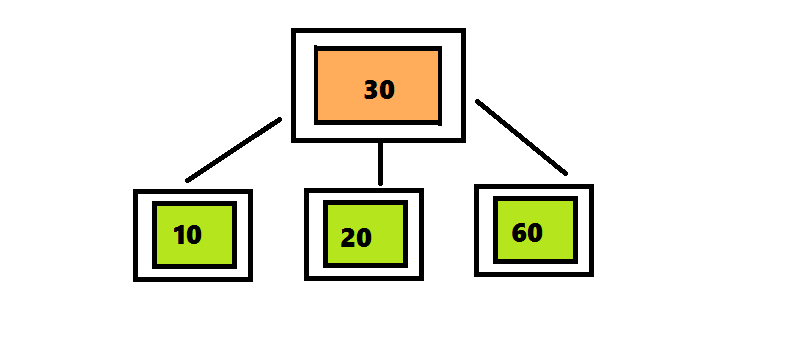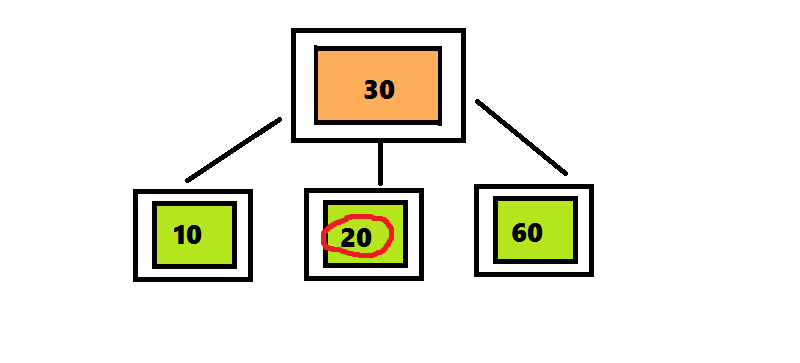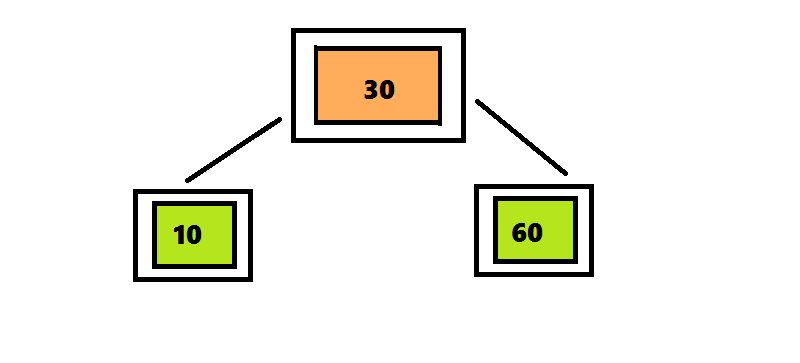
Алгоритм вставки элемента в 2-3-4 дерево отличается от алгоритма вставки элемента в 2-3 дерево только те, что узлы, которые содержат 4 элемента разделяются сразу после обнаружения.В дереве 2-3 алгоритм поиска проходил по пути от корня до листа, а затем возвращался обратно, разделяя узлы. Чтобы избежать этого возвращения, алгоритм вставки элемента в 2-3-4 дерево разделяет четырехместные узлы сразу при обнаружении на пути от корня к листу. Поиск позиции для вставки начинается с корня, представляющего собой четырехместный узел <10 30 60>. Перемещая число 30 вверх, разделяем его на три части. Поскольку этот узел является корнем, нужно создать новый корень, поместить в него число 30 и присоединить к нему два дочерних узла. Продолжаем поиск числа 20, проверяя левое поддерево корня, поскольку число 20 меньше 30.

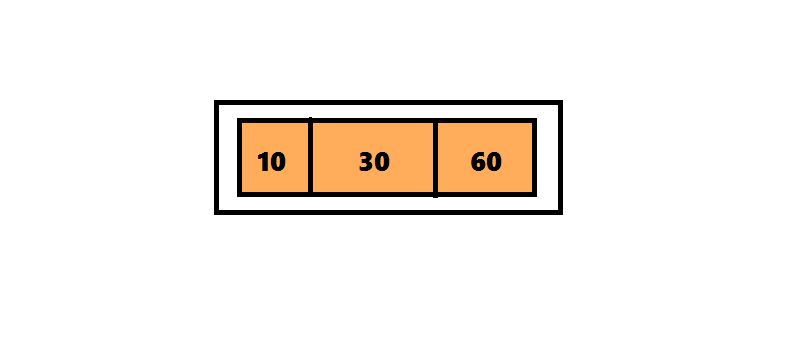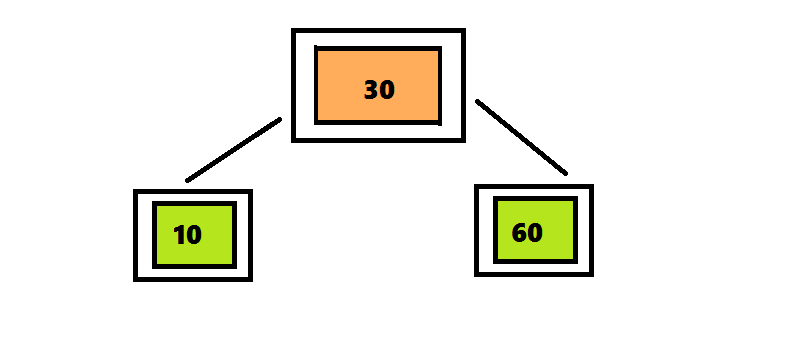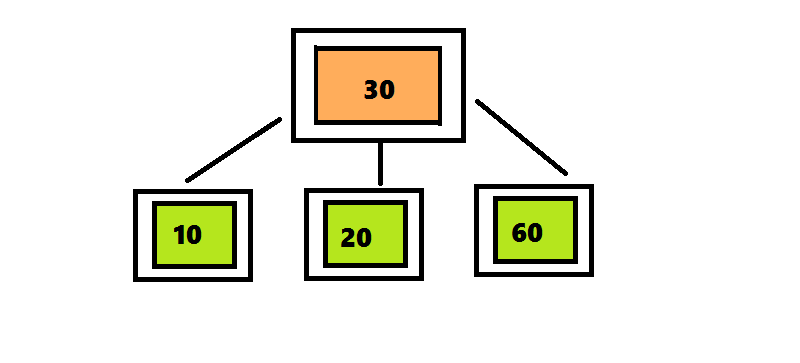
Удаление узла из 2-3-4 дерева

Алгоритм удаления заключается в том, что сначала выполняется поиск узла, содержащего заданный элемент. Потом ищем симметричного преемника этого узла. Затем меняем их местами с элементом, так чтобы удаление всегда выполнялось из листа. Если лист содержит 3 или 4 элемента, мы просто удаляем из него искомый элемент. Главное отличие состоит в том, что в 2-3-4 дереве нам не нужно возвращаться в корень и перестраивать дерево, как мы это делаем в 2-3 дереве.



Закончить свой рассказ я бы хотел словами своего предшественника: «При написании курсового проекта по этой теме, я понял, что информации в Рунете практически нет, поэтому решил внести свои пару копеек в это дело, рассказав заинтересованному сообществу об этой структуре данных.»

P.S.: во время написания я черпал знания из книги «Абстракция данных и решение задач на C++. Стены и зеркала» 3-е издание, авторы: Френк М. Каррано, Джанет Дж. Причард, советую всем ее для прочтения и огромное спасибо вам, читатели, за уделенное материалу внимание.