В предыдущей публикации мы подключали дешевый китайский LCD экран к плате STM32L4 Discovery. Теперь мы попробуем реализовать на этой комбинации что-то выходящее за рамки традиционного моргания светодиодом, а именно анализатор звукового спектра, который использует имеющийся на плате микрофон. Заодно я расскажу, как пользоваться операционной системой FreeRTOS, и зачем она нужна, а также почему в нотной октаве 12 нот, и чем 53 ноты лучше, чем 12.

Оцифровка звука

Мы хотим получать сигнал с микрофона, вычислять его спектр с помощью быстрого преобразования Фурье (FPU нам в помощь) и показывать результат на LCD в виде 'цветного водопада'. Силу звука будем кодировать цветом. Будем рисовать с краю дисплея строку пикселей, где самый левый пиксель будет соответствовать минимальной частоте, а самый правый — максимальной, при этом предыдущая картинка будет смещаться на одну строку, освобождая место для новой строки. Наш микроконтроллер слишком сложен, чтобы начать с нуля, поэтому начнем с примера из комплекта STM32Cube, который называется DFSDM_AudioRecord. Что такой DFSDM? Это Digital Filter for Sigma-Delta Modulation. Дело в том, что в отличие от старых добрых аналоговых микрофонов, тот, что стоит на плате Discovery, выдает сигнал не в виде напряжения, пропорционального звуковому давлению, а в виде последовательности нулей и единиц с тактовой частотой в несколько мегагерц. Если пропустить эту последовательность через фильтр низких частот, то получится тот самый аналоговый сигнал. В предыдущих моделях микроконтроллеров приходилось делать цифровой фильтр, чтобы получить звуковой сигнал в цифровом виде. Теперь в микроконтроллере есть специальный модуль для этого, и все, что требуется, — это настроить его на старте программы. Для этого можно или углубиться в чтение документации, или воспользоваться готовым примером. Я пошел по второму пути. Следующая картинка иллюстрирует внутреннюю структуру программы DFSDM_AudioRecord.



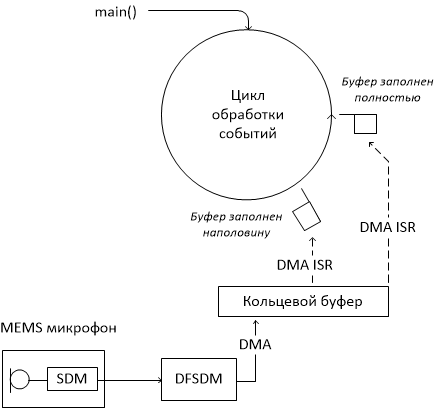
Оцифрованный звук с помощью DMA попадает в кольцевой буфер. DMA вызывает прерывание дважды: один раз — когда буфер заполнен наполовину, второй раз — когда он заполнен полностью. Процедура обработки прерываний просто выставляет соответствующий флажок. Функция main() после инициализации исполняет бесконечный цикл, где проверяются эти флажки и, если флажок выставлен, копируется соответствующая половина буфера. Пример копирует данные в другой буфер, откуда они, опять-таки с помощью DMA, отправляются на усилитель наушников. Я оставил эту функциональность, добавив вычисление спектра звукового сигнала.

Когда задач много

Прямолинейный способ добавить новую функциональность в наш код — добавить еще флажков и написать функции, которые будут вызываться, если эти флажки выставлены. В результате обычно получается каша из флажков, функций-обработчиков и глобального контекста, который вынужден быть глобальным, поскольку решение одной задачи разбивается на множество мелких шагов, реализованных отдельными функциями — обработчиками событий. Альтернативный способ — поручить управление задачами операционной системе, например FreeRTOS. Это позволяет значительно упростить логику за счет того, что каждая задача решается в рамках своего цикла обработки событий, которые взаимодействуют друг с другом посредством функций операционной системы. Например, мы можем добавить задачу обработки данных в виде отдельного цикла, который будет ждать готовности данных на синхронизационном примитиве — семафоре. Семафор устроен очень просто: вы можете пройти его, если флажок поднят, при этом флажок автоматически опускается. Поднимет флажок в нашем случае источник данных, когда подготовит данные для другой задачи. Подобным образом можно создавать произвольные цепочки из задач-источников данных и задач-потребителей данных подобно тому, как это происходит, например, в операционной системе линукс.



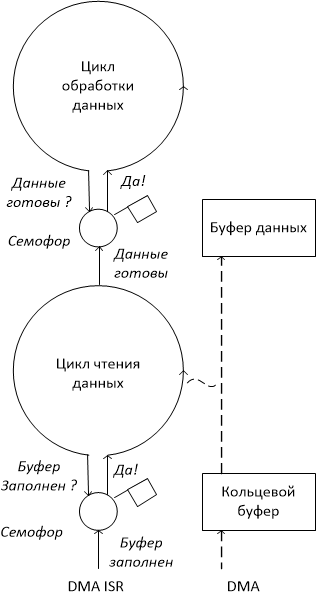
Конечно, одновременность исполнения задач — это иллюзия, особенно, когда вычислительное ядро всего одно. В этом случае мы можем говорить о том, что у нас есть единственный поток исполнения программы процессором. Семафоры, как и другие синхронизационные примитивы, играют роль волшебной кроличьей норы, в которую проваливается поток исполнения, чтобы вынырнуть в другой задаче.

Подключить FreeRTOS к своему проекту достаточно просто. Нужно лишь заменить бесконечный цикл, которым обычно заканчивается функция main() в микроконтроллере, на вызов osKernelStart(). После этого компилятор объяснит вам, чего именно ему не хватает для компиляции. Все действия, которые вы до этого выполняли в цикле, нужно перенести в отдельную задачу и зарегистрировать ее с помощью вызова xTaskCreate. После этого вы сможете добавить еще столько задач, сколько захотите. Нужно иметь ввиду, что между вызовами xTaskCreate и osKernelStart лучше не размещать никакого кода, работающего с железом, поскольку здесь системный таймер может работать неправильно. Вызов обработчика таймера операционной системы osSystickHandler() нужно добавить в SysTick_Handler(), а две функции SVC_Handler и PendSV_Handler убрать из своего кода, поскольку они реализованы в коде ОС. При регистрации задач важно не ошибиться с размером стека. Если он окажется слишком мал, вы получите краши в самых неожиданных местах. Первым при переполнении стека страдает сама структура, описывающая задачу. В IAR есть возможность посмотреть список задач. Если вы видите в нем задачу с измененным именем, значит нужно увеличить размер стека.

Вычисляем спектр

Для вычисления спектра мы воспользуемся быстрым преобразованием Фурье. Соответствующая функция уже есть в библиотеке. Она получает буфер, заполненный комплексными данными, и формирует результат там же. Соответственно, на входе ей нужен буфер, где оцифрованный звук чередуется с нулями (комплексная часть 0). На выходе мы получаем комплексные числа, для которых сразу вычисляем квадрат модуля, сложив квадраты действительной и мнимой части. Мы делаем это только для половины буфера, поскольку спектр симметричен. Вторая половина нам понадобилась бы, если бы мы захотели сделать обратное преобразование, но для простого показа спектра она не нужна. Некоторые дополнительные усилия необходимы для того, чтобы иметь возможность вычислять спектр в разных спектральных диапазонах. Чтобы получить спектр для низких частот, я аккумулирую данные за несколько циклов чтения буфера, эффективно снижая частоту дискретизации звука, которая изначально составляет 44.1kHz. В итоге получается 6 диапазонов — 20kHz, 10kHz, 5kHz, 2600Hz, 1300Hz, 650Hz. Для переключения диапазонов используется джойстик и отдельная задача. Джойстик также выполняет функции запуска / останова 'водопада', а также регулировки чувствительности. Показывать спектр удобнее в логарифмических единицах (децибелах), поскольку его динамический диапазон обычно весьма велик, и в линейном масштабе мы сможем различить лишь самые сильные составляющие спектра. Логарифм считается довольно долго даже на FPU, поэтому я заменил реальный логарифм кусочно-линейной аппроксимацией, которую легко получить, зная формат представления числа в float32. Старший бит — это знак. Следующие 8 бит — двоичная экспонента плюс 127. Оставшиеся биты — это дробная часть мантиссы при том, что целая часть равна 1 (нюансы денормализованных чисел для простоты опустим). Значит, выделив из float32 экспоненту и прихватив несколько старших бит мантиссы, можно получить неплохую аппроксимацию логарифма. Полученное число мы с помощью предварительно заготовленной таблицы преобразуем в RGB код для показа на LCD. Получается цветовая шкала на 90 или 60 децибел. Уровень громкости, соответствующий нулю этой шкалы, можно настраивать, нажимая джойстик вверх и вниз.

Выводим картинку — о пользе чтения даташитов

Теперь нам осталось вывести картинку и оживить наш 'водопад'. Прямолинейный способ сделать это — хранить картинку со всего экрана в буфере, обновлять ее там и перерисовывать каждый раз, когда появляются новые данные. Мало того, что это решение крайне неэффективное, у нас еще и недостаточно памяти, чтобы хранить всю картинку. Казалось бы, у самой LCD достаточно памяти для этого, и она должна уметь делать с ней что-то интересное. Действительно, изучение даташита позволило обнаружить доселе никем не использованную команду скроллинга, которая позволяет динамически менять способ отображения памяти контроллера LCD на экран. Представим себе, что память — это замкнутая в кольцо лента, которую вы видите под стеклом экрана. Команда Vertical Scrolling Start Address (0x37) позволяет задать позицию на ленте, соответствующую верхнему краю экрана. Значит, все, что нам нужно, чтобы оживить 'водопад' — это записать в эту позицию новый спектр и прокрутить ленту памяти. Соответствующий код был добавлен в драйвер LCD, позаимствованный у уважаемого Peter Drescher, и адаптированный как описано тут. Единственный недостаток подобного подхода: скроллинг работает только вдоль длинной стороны экрана. Соответственно, для вывода спектра доступна только короткая сторона.

Почему в октаве 12 нот ?

Перейдем к практическим применениям нашего устройства. Первое, что легко увидеть на спектре, это гармоники, то есть частоты, кратные частоте основного тона. Особенно много их в голосе. Есть они и в звуках, которые издают музыкальные инструменты. Легко понять, почему ноты соседних октав различаются по частоте в 2 раза: тогда ноты более высокой октавы совпадают по частоте со второй гармоникой нот низкой октавы. Говорят, что при этом они звучат «в унисон». Чуть сложнее разобраться в том, почему в октаве 12 нот — семь основных (белые клавиши на клавиатуре фортепьяно) плюс 5 дополнительных (черные клавиши). Дополнительные ноты обозначаются через основные с диезными и бемольными знаками, хотя по сути никакой разницы между ними и основными нотами нет — все 12 нот образуют геометрическую прогрессию так, что отношение частот между соседними нотами равно корню 12-й степени из 2. Смысл такого деления октавы на ноты в том, чтобы для любой ноты нашлись другие ноты, отличающиеся от нее по частоте в полтора раза — такая комбинация называется квинтой. Ноты, образующие квинту, звучат в унисон потому, что вторая гармоника одной ноты совпадает по частоте с третьей гармоникой другой ноты. На фото ниже показаны спектры нот До и Соль, образующих квинту, совпадающие гармоники обведены желтым.



Как же получилось, что нот 12? Поскольку ноты образуют геометрическую прогрессию, перейдем к логарифмам. ln(1.5)/ln(2) = 0.58496… Близкое значение получается у дроби 7/12 = 0.583… То есть, семь полутонов (интервалов между соседними нотами) оказываются весьма близки к квинте — 1.498. Интересно, что гораздо большую точность дает дробь 31/53 = 0.58491.., так что квинта отличается от 1.5 только в пятом знаке после запятой. Этот факт не остался незамеченным, но музыкальные инструменты с 53 нотами в октаве не получили распространения. Их сложно настраивать, на них сложно играть, а процент людей, способных почувствовать разницу с обычными инструментами, исчезающе мал.

Исходный код

Лежит тут. Для компиляции использовался IAR Embedded Workbench for ARM 7.50.2. Никаких других библиотек для компиляции не требуется.