В предыдущей части статьи был разобран общий принцип работы системы: мы увидели, что двумя основными её блоками являются интерполятор и нумератор. Мы построили схему взаимодействия, а также полностью обсудили реализацию интерполятора. В этой части мы разберём реализацию нумератора: обратимой функции, переводящей набор значений ключевых полей в натуральное число (BigInteger) таким образом, что набор  меньше набора
меньше набора  с точки зрения СУБД тогда и только тогда, когда
с точки зрения СУБД тогда и только тогда, когда  . Говоря проще — научимся интерполировать наборы значений и, что самое интересное, строки:
. Говоря проще — научимся интерполировать наборы значений и, что самое интересное, строки:

Назовём мощностью типа данных количество различных значений, которые представимы при помощи этого типа. Тип BIT, например, имеет мощность 2, а тип INT — 232. Пусть типы данных составного ключа имеют мощности . Тогда общее количество возможных комбинаций значений ключевых полей составного ключа равно
. Тогда общее количество возможных комбинаций значений ключевых полей составного ключа равно  . Допустим, что мы уже умеем вычислять функции нумераторов для значения каждого из полей,
. Допустим, что мы уже умеем вычислять функции нумераторов для значения каждого из полей,  — порядковый номер значения
— порядковый номер значения  -го поля. Тогда функция нумератора составного ключа может быть представлена через функции нумераторов каждого из полей как
-го поля. Тогда функция нумератора составного ключа может быть представлена через функции нумераторов каждого из полей как

Легко проверить, что 1) значение имеет наибольший вес,
имеет наибольший вес,  — наименьший, и основное требование к функции-нумератору выполнено, 2)
— наименьший, и основное требование к функции-нумератору выполнено, 2)  .
.
Сразу отметим, что вычисление напрямую по приведённой формуле требует
напрямую по приведённой формуле требует  операций умножения, и лучше воспользоваться аналогом схемы Горнера, чтобы уменьшить количество умножений до
операций умножения, и лучше воспользоваться аналогом схемы Горнера, чтобы уменьшить количество умножений до  при том же количестве сложений:
при том же количестве сложений:

Теперь нам нужен алгоритм вычисления обратной функции . Заметим, что значение
. Заметим, что значение  похоже на интерпретацию числа
похоже на интерпретацию числа  в позиционной системе счисления, только с постоянно меняющимся от «цифры» к «цифре» основанием. Соответветвенно, превратить значение
в позиционной системе счисления, только с постоянно меняющимся от «цифры» к «цифре» основанием. Соответветвенно, превратить значение  обратно в набор «цифр» можно по алгоритму, являющемуся вариацией алгоритма представления числа в систему счисления с заданным основанием (здесь value =
обратно в набор «цифр» можно по алгоритму, являющемуся вариацией алгоритма представления числа в систему счисления с заданным основанием (здесь value =  , keys[i].cardinality() =
, keys[i].cardinality() =  ):
):
С составным ключом разобрались, осталось построить нумераторы для встречающихся на практике типов.
Если длина строки не ограничена, то задача создания нумератора невыполнима: между строками 'a' и 'b' в лексикографическом порядке находится бесконечно много строк 'aa', 'aaa', 'aaaa'..., а между любыми двумя натуральными числами находится всегда конечное количество натуральных чисел. Математик скажет, что порядки множества лексикографически упорядоченных строк и множества натуральных чисел неизоморфны. К счастью, в известных нам СУБД индекс можно построить только по строке ограниченной длины, и это в корне меняет дело.
Если алфавит содержит символов, то общее количество строк длины не более
символов, то общее количество строк длины не более  в этом алфавите равно
в этом алфавите равно

Здесь единица соответствует пустой строке, — количество строк из одного символа,
— количество строк из одного символа,  — количество строк из двух символов и т. д., а в итоге получается старая добрая сумма геометрической прогрессии.
— количество строк из двух символов и т. д., а в итоге получается старая добрая сумма геометрической прогрессии.
Представим теперь произвольную строку длины
длины  как массив
как массив  , где
, где  — номер
— номер  -го символа строки в алфавите (считая с нуля), позиции символов в строке тоже считаем с нуля. Тогда строка
-го символа строки в алфавите (считая с нуля), позиции символов в строке тоже считаем с нуля. Тогда строка  в простом лексикографическом порядке будет иметь номер
в простом лексикографическом порядке будет иметь номер

Для оптимизации вычисления и обратной функции необходимо заранее заготовить массив коэффициентов
и обратной функции необходимо заранее заготовить массив коэффициентов

Разумеется, пользоваться этой формулой напрямую при заготовке значений не нужно: сэкономить на арифметических операциях можно, заметив, что все
не нужно: сэкономить на арифметических операциях можно, заметив, что все  являются частичными суммами геометрической прогрессии, которую можно вычислять «на ходу» при заполнении массива
являются частичными суммами геометрической прогрессии, которую можно вычислять «на ходу» при заполнении массива  .
.
Алгоритм для вычисления обратной функции , как и в случае нумератора составного ключа, является вариацией алгоритма преобразования числа в систему счисления с произвольным основанием. Необходимо только на каждом шаге перед получением очередного символа вычитать единицу, помня о первом слагаемом в формуле для
, как и в случае нумератора составного ключа, является вариацией алгоритма преобразования числа в систему счисления с произвольным основанием. Необходимо только на каждом шаге перед получением очередного символа вычитать единицу, помня о первом слагаемом в формуле для  :
:
Порядок, в котором база данных сортирует строковые значения, в действительности отличается от простого лексикографического и использует так называемые правила сопоставления (Unicode collation rules).
Базой данных при сравнении строк с учётом этих правил каждый символ рассматривается в трёх аспектах: собственно символ, его регистр (case) и вариант написания (accent). Например, русская буква «е» в большинстве случаев рассматривается как имеющая два варианта написания, каждый из которых имеет два регистра: е, Е; ё, Ё. Это позволяет при сортировке, нечувствительной к варианту написания (accent insensitive), не различать «е» и «ё», а при сортировке, нечувствительной к регистру (case insensitive), не различать строчные и заглавные буквы. При этом, что считать отдельной буквой, а что — вариантом написания другой буквы, зависит от культурных традиций и может различаться даже в языках, использующих один и тот же алфавит.
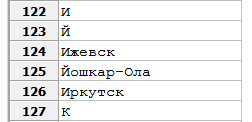
Например, если в русской культурной традиции ещё встречаются разногласия о статусе буквы «ё», то ни у кого не вызывает сомнения, что «и» и «й» — это разные буквы. В алфавитном перечне городов «Йошкар-Ола» должна следовать после «Иркутска», каков бы ни был режим сортировки. Если, однако, в базе данных PostgreSQL задать accent insensitive collation English-US и ввести в таблицу перечень городов, то, отсортировав их по названию, можно обнаружить, что «Йошкар-Ола» будет следовать перед «Иркутском», хотя и после «Ижевска». Причина, разумеется, в том, что выбранный набор правил сопоставления считает «й» не самостоятельным символом, а вариантом написания буквы «и»:
Общий алгоритм сравнения строк с учётом правил сопоставления следующий:
Все эти тонкости существенны для реализации нашей задачи, т. к. адекватная работа грида возможна лишь в том случае, когда значения, возвращаемые нумератором, возрастают на возрастающем (с точки зрения базы данных!) наборе аргументов.
Таким образом, нам, во-первых, необходимо модифицировать алгоритм работы нумератора для строк таким образом, чтобы он учитывал правила сопоставления, а во-вторых, необходимо уметь задавать различные правила сопоставления, «обучая» грид работе с той или иной базой данных.
Первая из этих задач относительно проста с учётом уже полученных результатов. Всякое строковое значение необходимо рассматривать не как одномерный массив символов , а как массив трёхкомпонентных значений (если угодно — векторов)
, а как массив трёхкомпонентных значений (если угодно — векторов)  ,
,  . Здесь
. Здесь  — номер
— номер  -го символа в алфавите,
-го символа в алфавите,  — его же вариант написания,
— его же вариант написания,  — его же регистр. Тогда работу со строковым полем можно производить аналогично работе с составным ключом, состоящим из трёх полей.
— его же регистр. Тогда работу со строковым полем можно производить аналогично работе с составным ключом, состоящим из трёх полей.
Если известны — количество символов в алфавите,
— количество символов в алфавите,  — максимальное число вариантов написания и
— максимальное число вариантов написания и  — максимальное число регистров (в известных нам языках
— максимальное число регистров (в известных нам языках  : «прописные» и «строчные»), то
: «прописные» и «строчные»), то

где — вычисленное по первым компонентам строки значение формулы
— вычисленное по первым компонентам строки значение формулы  (
( ),
),

Обратную функцию легко построить, используя уже вышеизложенные принципы: сперва необходимо разделить на три компоненты
на три компоненты  ,
,  и
и  , затем получить массив трёхкомпонентных значений, на основании которого восстанавливается исходная строка.
, затем получить массив трёхкомпонентных значений, на основании которого восстанавливается исходная строка.
В стандартной библиотеке Java имеются абстрактный класс java.text.Collator и его реализация java.text.RuleBasedCollator. Назначением этих классов является сравнение строк с учётом разнообразных правил сопоставлений. Доступна обширная библиотека готовых правил. К сожалению, эти классы не пригодны для использования с какой-либо иной, чем сравнение строк, целью: вся информация о правилах сопоставлений инкапсулирована, и её невозможно получить, штатным образом используя системную библиотеку.
Поэтому для решения нашей задачи понадобилось создать интерпретатор правил сопоставлений самостоятельно.
Эту задачу облегчило изучение класса RuleBasedCollator. Главной заимствованной идеей стал язык определения правил сортировки, формальное описание которого приведено в документации. Понять принцип работы этого языка проще всего, рассмотрев пример правила:
Следующие знаки являются служебными в языке правил сопоставления:
При помощи выражений, подобных вышеприведённому, можно определить правила, соответствующие различным сопоставлениям различных баз данных. Т. к. язык правил сопоставлений достаточно примитивен, для разбора выражений на нём оказалось достаточно алгоритма, работающего как детерминированный конечный автомат. В итоге по заданному выражению правил мы получаем экземпляр класса, способный
Нумератор для строковых значений построен, можно собирать систему по схеме, описанной в первой части статьи.
Уже после того, как система была собрана и началось тестирование, открылись особенности, повлекшие за собой некоторые доработки.
Во-первых, важным нюансом при практической реализации явилась необходимость отдельной обработки передвижения бегунка прокрутки на малый шаг.
Прокрутка на одну строку вверх или вниз происходит при щелчке мышью на стрелки «вверх» и «вниз» вертикальной полосы прокрутки. При щелчке на свободное поле полосы прокрутки сверху или снизу от бегунка происходит прокрутка на фиксированное (малое) количество строк. В этих случаях пользователь ожидает сдвига всех видимых на экране строчек на фиксированное число позиций. Интерполятор, не набравший достаточно интерполяционных точек, может повести себя непредсказуемо, отбросив отображаемую пользователю картину слишком далеко назад или вперёд, и после уточнения позиция полосы прокрутки не будет соответствовать тому, что хотел пользователь.
В этом случае, однако, использование интерполятора и не оправдано. Если известен предыдущий набор значений ключевых полей, то получить одну предыдущую (или одну следующую) запись можно быстрым запросом к базе данных. Проделав это несколько раз, можно получить несколько предыдущих или последующих записей всё ещё за незаметное для пользователя время.
После извлечения этих данных, помимо отображения их пользователю, можно пополнить интерполяционную таблицу ещё одной точкой, не прибегая к запросу на подсчёт записей, т. к. полученная запись имеет номер, отличающийся от предыдущей на известное значение.
Другим важным нюансом при практической реализации явилась необходимость заполнять интерполяционную таблицу данными до того, как пользователь начинает прокрутку грида.
Нет ничего удивительного в том, что номера комбинаций на основе данных в реальной таблице распределяются на числовой прямой очень неравномерно. Поэтому, при недостаточном количестве точек в интерполяционной таблице, пользователь, сместив бегунок полосы прокрутки на некоторое расстояние, может получить после уточнения позиции сильный «отскок» вперёд или назад. В итоге реальная позиция просматриваемых данных переместится или намного дальше, или, наоборот, намного ближе, чем хотел пользователь.
на основе данных в реальной таблице распределяются на числовой прямой очень неравномерно. Поэтому, при недостаточном количестве точек в интерполяционной таблице, пользователь, сместив бегунок полосы прокрутки на некоторое расстояние, может получить после уточнения позиции сильный «отскок» вперёд или назад. В итоге реальная позиция просматриваемых данных переместится или намного дальше, или, наоборот, намного ближе, чем хотел пользователь.
Испытания показывают, что погрешность на 20-25% от длины полосы прокрутки при позиционировании является психологически допустимой, но не более того. Поэтому после отображения грида пользователю желательно обеспечить, чтобы максимальная длина «отскока» составляла не более, чем 20-25% длины полосы прокрутки даже в самом начале работы, когда статистика в интерполяционной таблице ещё не накоплена.
Сделать это эффективным образом можно в параллельном потоке выполнения, запускаемом после отображения грида. В этом потоке выполняется серия уточняющих запросов, по результатам которых пополняется интерполяционная таблица. Значение комбинации ключей для уточняющего запроса всякий раз выбирается как лежащее посередине самого большого зазора в значениях порядковых номеров записей интерполяционной таблицы. Процесс выполняется до тех пор, пока ширина максимального зазора не уменьшится до желаемого размера, либо до достижения ограничения на количество итераций.
Грид по приведённым здесь принципам был реализован на языке Java с использованием PostgreSQL в качестве СУБД. В качестве одного из нагрузочных тестовых наборов данных используется база данных КЛАДР, содержащая 1075429 названий улиц населённых пунктов России, сортировка ведётся по различным полям и их комбинациям. Все изложенные здесь принципы работают. При постоянном перемещении бегунка вертикальной полосы прокрутки для пользователя создаётся полная иллюзия прокручивания всех записей в реальном времени, через малое время после окончания прокручивания (когда срабатывает уточняющий запрос и в интерполяционную таблицу добавляется ещё одна точка) позиция бегунка полосы прокрутки уточняется, перескакивая на небольшое расстояние. Позиционирование позволяет моментально отобразить нужные записи и сразу же приблизительно выставить бегунок полосы прокрутки, через малое время его позиция также уточняется. По мере работы с гридом и накопления интерполяционных точек, «отскоки» становятся всё менее и менее заметными.
По проделанной работе я готовлю научную публикацию, и вы можете также ознакомиться с препринтом научной версии этой статьи на arxiv.org.

Нумератор для составного ключа
Назовём мощностью типа данных количество различных значений, которые представимы при помощи этого типа. Тип BIT, например, имеет мощность 2, а тип INT — 232. Пусть типы данных составного ключа имеют мощности
Легко проверить, что 1) значение
Сразу отметим, что вычисление
Теперь нам нужен алгоритм вычисления обратной функции
BigInteger v = value;
BigInteger[] vr;
for (int i = keys.length - 1; i >= 0; i--) {
vr = v.divideAndRemainder(keys[i].cardinality());
keys[i].setOrderValue(vr[1]);
v = vr[0];
}
Нумераторы для примитивных типов данных
С составным ключом разобрались, осталось построить нумераторы для встречающихся на практике типов.
- Нумерация значений типа BIT тривиальна: false — 0, true — 1.
- Нумерация значений типа INT немногим сложенее: INT-значение (32-битовое целое со знаком) есть число между -2147483648 и 2147483647. Таким образом, нумератор для типа INT есть просто
. Конечно, выполнять сложение следует, уже приведя
к типу BigInteger. Обратная функция
.
- Подобным же образом можно построить нумератор и для 64-битовых целых чисел со знаком (прибавлять надо 9223372036854775808).
- Числа DOUBLE (двойной точности с плавающей точкой), представленные в формате IEEE 754, обладают тем свойством, что их можно (за несущественными исключениями вроде NaN и ±0) сравнивать как целые 64-битовые числа со знаком. Например, в Java получить для значения с типом double его 64-битовый образ в формате IEEE 754 можно с помощью метода Double.doubleToLongBits.
- Наконец, значения DATETIME, определяющие момент времени с точностью до миллисекунды, также могут быть сведены к 64-битовому целому числу со знаком, задающему так называемое «UNIX-время», т. е. количество миллисекунд от полуночи 1 января 1970 года. Например, в Java это делается при помощи метода Date.getTime().
- Строки (VARCHAR) требуют отдельного большого разговора.
Нумератор для строк (первое приближение)
Если длина строки не ограничена, то задача создания нумератора невыполнима: между строками 'a' и 'b' в лексикографическом порядке находится бесконечно много строк 'aa', 'aaa', 'aaaa'..., а между любыми двумя натуральными числами находится всегда конечное количество натуральных чисел. Математик скажет, что порядки множества лексикографически упорядоченных строк и множества натуральных чисел неизоморфны. К счастью, в известных нам СУБД индекс можно построить только по строке ограниченной длины, и это в корне меняет дело.
Если алфавит содержит
Здесь единица соответствует пустой строке,
Представим теперь произвольную строку
Доказательство этой формулы
производится, естественно, методом индукции. Действительно: если  , то единственный вариант — это пустая строка с номером 0.
, то единственный вариант — это пустая строка с номером 0.
Если , то пустая строка будет иметь номер 0, а каждая односимвольная будет иметь номер
, то пустая строка будет иметь номер 0, а каждая односимвольная будет иметь номер  . Единица прибавляется потому, что при сравнении строк пустая строка будет меньше любой односимвольной строки: 0 — '', 1 — 'a', 2 — 'b'…
. Единица прибавляется потому, что при сравнении строк пустая строка будет меньше любой односимвольной строки: 0 — '', 1 — 'a', 2 — 'b'…
Если ,
,  , то по-прежнему 0 — '', 1 — 'a'. Но теперь между строками 'a' и 'b' в пространстве лексикографически отсортированных строк находятся все возможные строки вида «'a' плюс любая строка длиной не более
, то по-прежнему 0 — '', 1 — 'a'. Но теперь между строками 'a' и 'b' в пространстве лексикографически отсортированных строк находятся все возможные строки вида «'a' плюс любая строка длиной не более  »: 'a', 'aa', 'aaa'..., 'aab'...:
»: 'a', 'aa', 'aaa'..., 'aab'...:

Количество таких строк равно , и окончательно для односимвольных строк
, и окончательно для односимвольных строк

Пусть к строке добавляется ещё один символ, при этом по-прежнему . В качестве последнего слагаемого добавляется номер этого символа с соответствующим весом (равным числу строк длиной
. В качестве последнего слагаемого добавляется номер этого символа с соответствующим весом (равным числу строк длиной  ). К первому слагаемому для каждого дополнительного символа добавляется единица, за счёт того, что строка, полученная отбрасыванием последнего символа, будет в лексикографическом порядке меньше любой из строк длиной
). К первому слагаемому для каждого дополнительного символа добавляется единица, за счёт того, что строка, полученная отбрасыванием последнего символа, будет в лексикографическом порядке меньше любой из строк длиной  .
.
Если
Если
Количество таких строк равно
Пусть к строке добавляется ещё один символ, при этом по-прежнему
Для оптимизации вычисления
Разумеется, пользоваться этой формулой напрямую при заготовке значений
Алгоритм для вычисления обратной функции
for (int i = 0; i < m; i++) {
r = r.subtract(BigInteger.ONE);
cr = r.divideAndRemainder(q[i]);
r = cr[1];
int c = cr[0].intValue();
arr[i] = c;
if (r.equals(BigInteger.ZERO)) {
if (i + 1 < m)
arr[i + 1] = END_OF_STRING;
break;
}
}
Нумератор для строк с учётом правил сопоставлений
Порядок, в котором база данных сортирует строковые значения, в действительности отличается от простого лексикографического и использует так называемые правила сопоставления (Unicode collation rules).
Базой данных при сравнении строк с учётом этих правил каждый символ рассматривается в трёх аспектах: собственно символ, его регистр (case) и вариант написания (accent). Например, русская буква «е» в большинстве случаев рассматривается как имеющая два варианта написания, каждый из которых имеет два регистра: е, Е; ё, Ё. Это позволяет при сортировке, нечувствительной к варианту написания (accent insensitive), не различать «е» и «ё», а при сортировке, нечувствительной к регистру (case insensitive), не различать строчные и заглавные буквы. При этом, что считать отдельной буквой, а что — вариантом написания другой буквы, зависит от культурных традиций и может различаться даже в языках, использующих один и тот же алфавит.
Например, если в русской культурной традиции ещё встречаются разногласия о статусе буквы «ё», то ни у кого не вызывает сомнения, что «и» и «й» — это разные буквы. В алфавитном перечне городов «Йошкар-Ола» должна следовать после «Иркутска», каков бы ни был режим сортировки. Если, однако, в базе данных PostgreSQL задать accent insensitive collation English-US и ввести в таблицу перечень городов, то, отсортировав их по названию, можно обнаружить, что «Йошкар-Ола» будет следовать перед «Иркутском», хотя и после «Ижевска». Причина, разумеется, в том, что выбранный набор правил сопоставления считает «й» не самостоятельным символом, а вариантом написания буквы «и»:

Общий алгоритм сравнения строк с учётом правил сопоставления следующий:
- Строки сравниваются посимвольно без учёта регистров и вариантов. Если обнаружено различие, возвращается результат («больше» или «меньше»).
- Если сортировка accent sensitive, сравниваются номера вариантов каждого из символов. Если обнаружено различие, возвращается результат.
- Если сортировка case sensitive, сравниваются регистры каждого из символов. Если обнаружено различие, возвращается результат.
- Если выход из алгоритма не произошёл до сих пор — строки равны.
Все эти тонкости существенны для реализации нашей задачи, т. к. адекватная работа грида возможна лишь в том случае, когда значения, возвращаемые нумератором, возрастают на возрастающем (с точки зрения базы данных!) наборе аргументов.
Таким образом, нам, во-первых, необходимо модифицировать алгоритм работы нумератора для строк таким образом, чтобы он учитывал правила сопоставления, а во-вторых, необходимо уметь задавать различные правила сопоставления, «обучая» грид работе с той или иной базой данных.
Первая из этих задач относительно проста с учётом уже полученных результатов. Всякое строковое значение необходимо рассматривать не как одномерный массив символов
Если известны
где
Обратную функцию легко построить, используя уже вышеизложенные принципы: сперва необходимо разделить
В стандартной библиотеке Java имеются абстрактный класс java.text.Collator и его реализация java.text.RuleBasedCollator. Назначением этих классов является сравнение строк с учётом разнообразных правил сопоставлений. Доступна обширная библиотека готовых правил. К сожалению, эти классы не пригодны для использования с какой-либо иной, чем сравнение строк, целью: вся информация о правилах сопоставлений инкапсулирована, и её невозможно получить, штатным образом используя системную библиотеку.
Поэтому для решения нашей задачи понадобилось создать интерпретатор правил сопоставлений самостоятельно.
Эту задачу облегчило изучение класса RuleBasedCollator. Главной заимствованной идеей стал язык определения правил сортировки, формальное описание которого приведено в документации. Понять принцип работы этого языка проще всего, рассмотрев пример правила:
<г,Г<д,Д<е,Е;ё,Ё<ж,Ж<з,З<и,И;й,Й<к,К<л,Л
Следующие знаки являются служебными в языке правил сопоставления:
- < — разделение символов,
- ; — разделение вариантов написания,
- , — разделение регистров.
При помощи выражений, подобных вышеприведённому, можно определить правила, соответствующие различным сопоставлениям различных баз данных. Т. к. язык правил сопоставлений достаточно примитивен, для разбора выражений на нём оказалось достаточно алгоритма, работающего как детерминированный конечный автомат. В итоге по заданному выражению правил мы получаем экземпляр класса, способный
- по заданным правилам получить значения
(количество символов), а также
(максимальное число вариантов) и
(максимальное число регистров) для вычисления прямых и обратных функций нумератора,
- по заданному символу определить три его компоненты (номер символа в алфавите, номер варианта, номер регистра),
- по заданной тройке компонентов определить символ.
Нумератор для строковых значений построен, можно собирать систему по схеме, описанной в первой части статьи.
Последние штрихи
Уже после того, как система была собрана и началось тестирование, открылись особенности, повлекшие за собой некоторые доработки.
Во-первых, важным нюансом при практической реализации явилась необходимость отдельной обработки передвижения бегунка прокрутки на малый шаг.
Прокрутка на одну строку вверх или вниз происходит при щелчке мышью на стрелки «вверх» и «вниз» вертикальной полосы прокрутки. При щелчке на свободное поле полосы прокрутки сверху или снизу от бегунка происходит прокрутка на фиксированное (малое) количество строк. В этих случаях пользователь ожидает сдвига всех видимых на экране строчек на фиксированное число позиций. Интерполятор, не набравший достаточно интерполяционных точек, может повести себя непредсказуемо, отбросив отображаемую пользователю картину слишком далеко назад или вперёд, и после уточнения позиция полосы прокрутки не будет соответствовать тому, что хотел пользователь.
В этом случае, однако, использование интерполятора и не оправдано. Если известен предыдущий набор значений ключевых полей, то получить одну предыдущую (или одну следующую) запись можно быстрым запросом к базе данных. Проделав это несколько раз, можно получить несколько предыдущих или последующих записей всё ещё за незаметное для пользователя время.
После извлечения этих данных, помимо отображения их пользователю, можно пополнить интерполяционную таблицу ещё одной точкой, не прибегая к запросу на подсчёт записей, т. к. полученная запись имеет номер, отличающийся от предыдущей на известное значение.
Другим важным нюансом при практической реализации явилась необходимость заполнять интерполяционную таблицу данными до того, как пользователь начинает прокрутку грида.
Нет ничего удивительного в том, что номера комбинаций
Испытания показывают, что погрешность на 20-25% от длины полосы прокрутки при позиционировании является психологически допустимой, но не более того. Поэтому после отображения грида пользователю желательно обеспечить, чтобы максимальная длина «отскока» составляла не более, чем 20-25% длины полосы прокрутки даже в самом начале работы, когда статистика в интерполяционной таблице ещё не накоплена.
Сделать это эффективным образом можно в параллельном потоке выполнения, запускаемом после отображения грида. В этом потоке выполняется серия уточняющих запросов, по результатам которых пополняется интерполяционная таблица. Значение комбинации ключей для уточняющего запроса всякий раз выбирается как лежащее посередине самого большого зазора в значениях порядковых номеров записей интерполяционной таблицы. Процесс выполняется до тех пор, пока ширина максимального зазора не уменьшится до желаемого размера, либо до достижения ограничения на количество итераций.
Практическая реализация
Грид по приведённым здесь принципам был реализован на языке Java с использованием PostgreSQL в качестве СУБД. В качестве одного из нагрузочных тестовых наборов данных используется база данных КЛАДР, содержащая 1075429 названий улиц населённых пунктов России, сортировка ведётся по различным полям и их комбинациям. Все изложенные здесь принципы работают. При постоянном перемещении бегунка вертикальной полосы прокрутки для пользователя создаётся полная иллюзия прокручивания всех записей в реальном времени, через малое время после окончания прокручивания (когда срабатывает уточняющий запрос и в интерполяционную таблицу добавляется ещё одна точка) позиция бегунка полосы прокрутки уточняется, перескакивая на небольшое расстояние. Позиционирование позволяет моментально отобразить нужные записи и сразу же приблизительно выставить бегунок полосы прокрутки, через малое время его позиция также уточняется. По мере работы с гридом и накопления интерполяционных точек, «отскоки» становятся всё менее и менее заметными.
***
По проделанной работе я готовлю научную публикацию, и вы можете также ознакомиться с препринтом научной версии этой статьи на arxiv.org.
Комментарии (6)

DigitalSmile
22.03.2016 10:19Спасибо за обе статьи, было интересно поглядеть на теоретическое обоснование. Присоединяюсь к вопрошающим — есть возможность увидеть реализацию?


Holms
Можно ли увидеть реализацию на Java?