Недавно на хабре была статья, в которой описывалось как можно определить, где находится точка по отношению к многоугольнику: внутри или снаружи. Подобная проблема встречается в геометрическом моделировании и в компьютерной графике достаточно часто. А так как метод, описанный в статье, был несколько не оптимален, а в комментариях был небольшой хаос, возникла мысль написать эту статью. Итак, какие алгоритмы существуют в современной компьютерной графике, чтобы определить, принадлежит ли заданная точка многоугольнику или нет.

Прежде, чем начать, хочу сразу описать проблему. Хотя сама проблема проста: у нас задан набор точек и задан порядок, в котором эти точки соединяются. И задана точка, которую мы тестируем на принадлежность. Подразумевается, что у нас многоугольник замкнутый, и в общем случае ребра многоугольника не пересекаются друг с другом, то есть он избавлен он самопересечений. Ограничений на количество вершин нет, то есть легко может быть задан многоугольник с миллионом вершин. Мы надеемся, что пользователь не задаст нам непонятно что, но и гарантировать это тоже не можем. И еще один нюанс: так как мы работаем с компьютерной графикой, что означает, что мы используем арифметику с плавающей точкой, которая хотя и позволяет оперировать с числами достаточно точно, все равно не избавлена от ошибок.

Ну вроде определились с проблемой, давайте теперь посмотрим, какие методы решения существуют.

Метод 1. Трассировка лучей

Начну я с того, который считается наиболее популярным в мире графики и игр: трассировка лучей. Вкратце, алгоритм можно описать следующим образом:

1. Из тестируемой точки выпускаем луч либо в заранее заданном, либо в произвольном направлении.
2. Считаем количество пересечений с многоугольником.
3. Если количество пересечений четное, мы находимся снаружи. Если количество пересечений нечетное, мы – внутри.

Звучит просто, не правда ли? И правда, это самый простой метод. Он в итоге сводится к некоторому количеству пересечений отрезка (грани многоугольника) и луча, то есть по сути пересечения двух прямых и тестирования полученной точки на принадлежность лучу и отрезку. В самом простом случае придется пересечь луч со всеми отрезками, при использовании деревьев (квадратичных, бинарных или BVH), можно сократить это количество. В целом говорят, что алгоритмическая сложность этого алгоритма O(log n), где n – количество ребер в многоугольнике.

Метод простой, но, к сожалению, в общем случае его лучше не применять. Причиной этого является случай, когда мы пересекаем лучом вершину многоугольника или ребро, которое частично совпадает с лучом. Иллюстрирую это на примере.



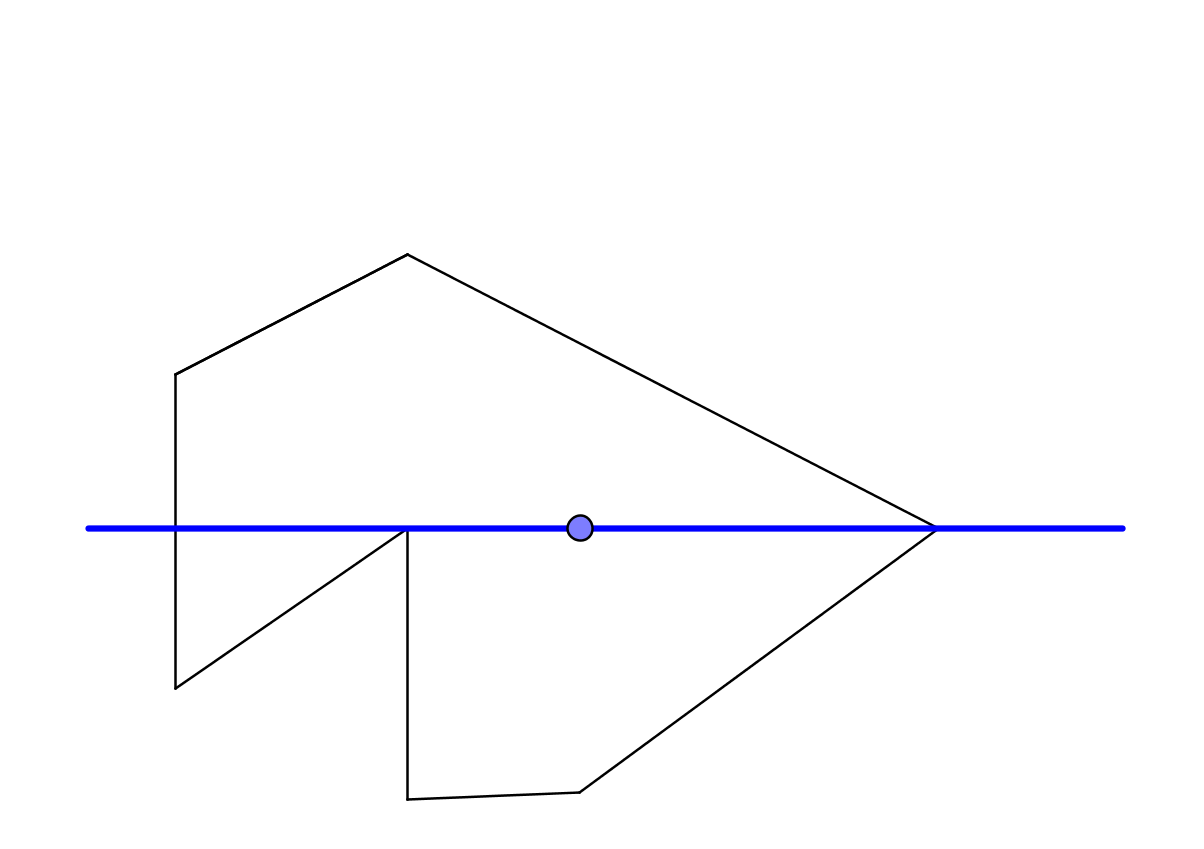
Допустим, у нас есть многоугольник, и есть точка. В самом начале мы договорились, что направление будет вдоль оси х. Выпускаем из точки луч в положительном направлении оси x и луч благополучно пересек многоугольник в вершине. Тут возникает вопрос, как именно мы проверяем такую ситуацию? Не забываем, что мы работаем с числами с плавающей точкой, и небольшие погрешности возможны. Перейдем в мир аналитической геометрии, чтобы можно было оперировать не просто геометрическими понятиями, а числами.

Уравнение каждого отрезка (грани многоугольника): a + t(b — a), где а – координаты одного конца отрезка, b – координаты другого конца отрезка. Очевидно, что если луч пересекает отрезок, t должно быть в интервале [0,1]. Если мы лучом пересекаем вершину, то t = 0 или t = 1. Это в идеальном мире математики. В реальном мире компьютерной алгебры у вас может получиться что-то вроде t = 1e-10. Или t = -1e-10. Или 0.99999999999998. Или 1.000000000000001. Поскольку пересечение двух прямых включает в себя процедуру деления, такое может запросто получиться. И что же в таком случае делать? Довериться компьютеру и считать, что если мы строго больше или равны нулю или строго меньше или равны единицы, то считаем это за пересечение, а иначе не считаем? Доверились и получили ситуацию, когда с одним ребром параметр t = -1e-20, с другим ребром t = 1.000000000000000001. В результате пересечениями это не считаем, и у нас луч благополучно проскочил мимо и результат оказывается неправильным.

Посмотрим в другом направлении. Отправили луч в отрицательном направлении. Там тоже не очень хорошо – луч пересекает вершину внутри многоугольника. Тоже может оказаться что угодно. Вместо горизонтального направления взять вертикальное? Никто не гарантирует, что вы опять не пересечете вершину. В конкретно выбранном мной примере наверху точка подобрана таким образом, что пересечение ее с лучом, параллельным оси y и идущий сверху вниз тоже пересекает многоугольник в вершине.

Причем если вы думаете, что пересечение с вершиной – это плохо, смотрите что еще может произойти:



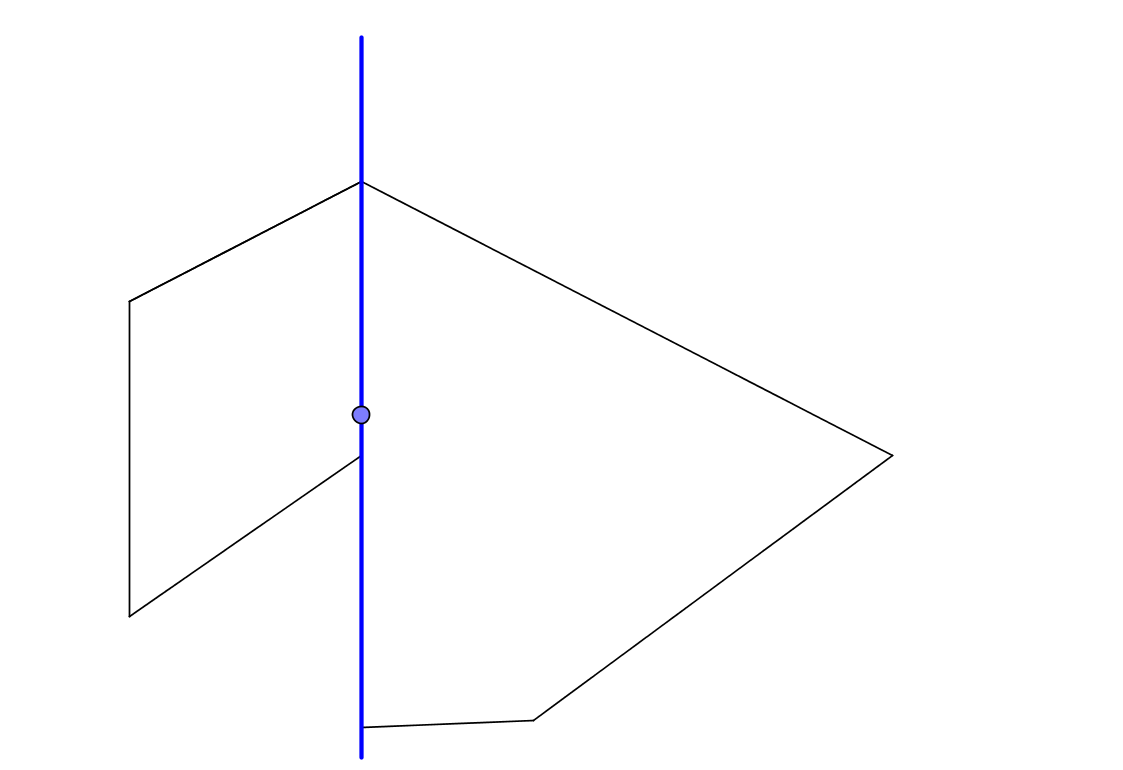
Здесь мы пересекаем луч с отрезком, который с этим лучом совпадает. Как быть в таком случае? А если не совпадает, а почти совпадает? А представьте себе, что в многоугольнике множество почти вырожденных ребер, как с таким пересекать?

Самое печальное во всей этой ситуации то, что нам вот кажется: «мне надо что-то очень простое для моих простых целей, меня такая ситуация не коснется». По закону Мерфи, к сожалению, именно такая ситуация возникает всякий раз когда ее совсем не ждешь. И поэтому я плавно перехожу ко второму методу.

Метод 2. Ближняя точка и ее нормаль

Вообще у этого метода есть страшное название angle weighted pseudo normals и связан он в понятием так называемых полей расстояний со знаком (signed distance fields). Но пугать лишний раз я никого не хочу, так что пусть будет просто ближняя точка и ее нормаль (то есть перпендикулярный вектор).

Алгоритм в данном случае такой:

1. Для тестируемой точки ищем ближайшую точку на многоугольнике. При этом помним, что ближайшая точка может быть не только на отрезке, но и в вершине.
2. Ищем нормаль ближайшей точки. Если ближняя точка лежит на ребре, то нормаль является вектор, перпендикулярный ребру и смотрящий наружу многоугольника. Если ближняя точка – одна из вершин, то нормалью является усредненный вектор ребер, прилежащих к вершине.
3. Вычисляем угол между нормалью ближайшей точки и вектором от тестируемой точки до ближайшей. Если угол меньше 90 градусов, то мы – внутри, иначе – снаружи.

Причем угол как таковой считать не обязательно, достаточно проверить знак косинуса этого угла. Если положительный – внутри, если отрицательный – снаружи. А поскольку нас интересует только знак косинуса, то по сути мы вычисляем знак скалярного произведения между двумя векторами.



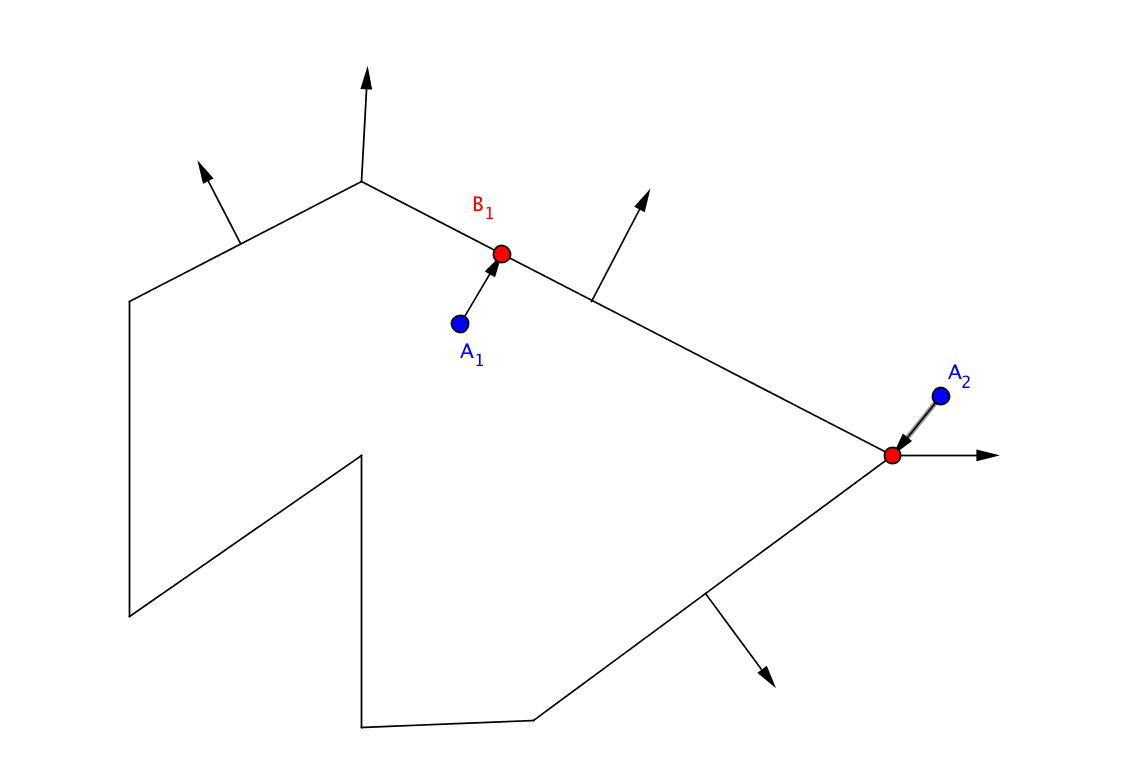
Рассмотрим пример. Точка A1, ближайшая точка для нее находится на ребре. Если все делаем правильно, нормаль к ребру параллельна вектору от тестируемой точки до ближайшей. В случае точки A1, угол между векторами = 0. Или почти нуль, так как из-за операций с плавающей точкой все возможно. Меньше 90 градусов, тестируемая точка A1 – внутри. Протестируем точку A2. У нее ближайшая точка – вершина, нормаль к которой – усредненная нормаль ребер прилегающих к этой вершине. Считаем скалярное произведение двух векторов, должно быть отрицательным. Мы – снаружи.

Так, вроде бы с сутью метода разобрались. Что там с производительностью и проблемами, связанной с плавающей точкой?

Как и в случае трассировки точек, производительность – O(log n), если использовать деревья для хранения информации о ребрах. С вычислительной точки зрения метод, хотя и имеет подобную сложность, будет несколько помедленнее, чем трассировка. Прежде всего оттого, что расстояние между точкой и ребром чуть более дорогостоящая операция, чем пересечение двух линий. Неприятности, связанные с плавающей точкой, возникают в этом методе, как правило недалеко от ребер многоугольника. Причем чем мы ближе к ребру, тем больше вероятность неправильного определения знака. К счастью, чем мы ближе к ребру, тем меньше расстояние. То есть если мы, например, говорим, что если полученное расстояние меньше заранее заданного минимального (это может быть константа вроде DBL_EPSILON или FLT_EPSILON), то точка принадлежит ребру. А если она принадлежит ребру, то мы уже сами решаем, часть ли многоугольника его ребро или нет (как правило – часть).

Описывая предыдущий метод, достаточно много было сказано о недостатках. Пришло время назвать несколько недостатков и этого способа. Прежде всего, этот метод требует, чтобы все нормали к ребрам были направлены в правильную сторону. То есть до того, как определять, снаружи мы или внутри, надо провести некую работу по вычислению этих нормалей и правильное их ориентирование. Очень часто, особенно когда на входе большая свалка из вершин и ребер, этот процесс не всегда прост. Если надо определить только для одной точки, процесс ориентации нормалей может занять большую часть времени, которую можно было бы потратить на что-то еще. Также, этот метод очень не любит, когда на вход подается многоугольник с самопересечениями. В начале я сказал, что в нашей задаче такой случай не рассматривается, но если бы он рассматривался, то этот метод мог выдать совершенно неочевидные результаты.

Но в целом метод неплох, особенно если у нас на входе многоугольник с большим количеством вершин и ребер, а точек на принадлежность надо протестировать много. Если же точек мало, трассировка лучей нестабильна, а хочется чего-то более-менее надежного, то есть и третий способ.

Метод 3. Индекс точки относительно многоугольника

Этот метод известен довольно давно, но в основном остается теоретическим, по большей части потому, что он не так эффективен, как предыдущие два. Вот его суть «на пальцах». Возьмем единичную окружность с центром в тестируемой точке. Потом каждую вершину многоугольника спроецируем на эту окружность лучами, которые проходят через вершину и тестируемую точку. Как-то примерно так:



На рисунке точки P1, P2 и так далее – вершины многоугольника, а точки P1’, P2’ и так далее – их проекции на окружность. Теперь когда мы рассматриваем ребро многоугольника, по проекциям можно определить, происходит ли вращение против часовой стрелке или по часовой стрелке при переходе от одной вершины к другой. Вращение против часовой стрелки будем считать положительным поворотом, а вращение по часовой стрелке – отрицательным. Угол, который соответствует каждому ребру – это угол между сегментами окружности через проекции вершин этого ребра. Так как поворот у нас может быть положительный или отрицательный, то и угол может быть положительный или отрицательный.

Если после этого сложить все эти углы, то сумма должна быть +360 или -360 градусов для точки находящейся внутри и 0 для точки снаружи. Плюс-минус тут неспроста. Если при задании порядка обхода многоугольник обходится против часовой стрелки, должно получиться +360. Если же порядок обхода ребер в многоугольнике против часовой стрелки, то получается -360. Во избежание числовых ошибок как правило делают так: делят получившуюся сумму на 360 и приводят к ближайшему целому. Получившееся число кстати и является тем самым индексом точки. Результат может быть один из трех: -1 означает что мы внутри и многоугольник обходим по часовой стрелке, 0 означает что мы снаружи, +1 означает что мы снаружи. Все остальное означает что мы где-то ошиблись, или что входные данные некорректны.

Алгоритм в этом случае следующий:

1. Устанавливаем сумму углов в 0.
2. Для всех ребер многоугольника:
   
   
   1. С помощью скалярного произведения вычисляем угол, образованный векторами начинающимся в тестируемой точке и заканчивающимися в концах ребра.
   2. Вычисляем векторное произведение этих же векторов. Если его z-компонента положительна – прибавляем угол к сумме углов, а иначе – вычитаем из той же суммы.
   
   Делим сумму на 2 если считаем в радианах или на 360 если считаем в градусах. Последнее маловероятно, но вдруг.
   Округляем результат до ближайшего целого. +1 или -1 значит, что мы внутри. 0 значит мы снаружи.
   


Рассмотрим пример. Есть многоугольник, порядок которого установлен против часовой стрелки. Есть точка А, которую мы тестируем. Для тестирования сначала вычисляем угол между векторами AP1 и AP2. Векторное произведение этих же векторов смотрит на нас, значит прибавляем к сумме. Переходим дальше и считаем угол между AP2 и AP3. Векторное произведение смотрит на нас, полученный угол вычитаем. И так далее.

Для конкретно этого рисунка я все посчитал и вот что получилось:

Точка А.

(AP1, AP2)=74.13, (AP2, AP3)=51.58, (AP3, AP4)=89.99, (AP4, AP5)=126.47, (AP5, AP1)=120.99.
sum=74.13-51.58+89.99+126.47+120.99=360. 360/360=1 Точка – внутри.

Точка B.

(BP1, BP2)=44.78, (BP2, BP3)=89.11, (BP3, BP4)=130.93, (BP4, BP5)=52.97, (BP5, BP1)=33.63.
sum=-44.78+89.11-130.93+52.97+33.63=0. Точка – снаружи.

И традиционно опишем плюсы и минусы данного подхода. Начнем с минусов. Метод прост математически, но не так-то эффективен с точки зрения производительности. Во-первых, его алгоритмическая сложность O(n) и, как ни крути, а все ребра многоугольника придется перебрать. Во-вторых, для вычисления угла придётся воспользоваться операцией арккосинуса и двумя операциями взятия корня (формула скалярного произведения и связь его с углом тем в помощь, кто не понимает, почему). Эти операции очень недешевы с точки зрения скорости, и, к тому же, погрешности связанные с ними могут быть существенны. И в третьих, алгоритм напрямую не определяет точку, лежащую на ребре. Либо – снаружи, либо – внутри. Третьего не дано. Впрочем, последний недостаток легко определяется: если хотя бы один из углов равен (или почти равен) 180 градусам, это автоматически означает ребро.

Недостатки метода в чем-то компенсируются его достоинствами. Во-первых, это самый стабильный метод. Если многоугольник на вход подан корректный, то результат получается корректный для всех точек, за исключением разве что точек на ребрах, но о них смотри выше. Более того, метод позволяет частично бороться с некорректными входными данными. Многоугольник самопересекается? Не беда, метод скорее всего определит большинство точек правильно. Многоугольник не замкнут или вообще не многоугольник а малоосмысленный набор сегментов? Метод определит точки верно в большом количестве случаев. В общем, всем метод хорош, но медленный и требует вычислений арккосинусов.

Чем бы хотелось закончить этот обзор? А тем, что методов для решения проблемы определения принадлежности точки многоугольнику существует не один и даже не два. Они служат для разных целей и некоторые более подходят в случаях, когда важна скорость, другие – когда важно качество. Ну и не забываем о том, что у нас непредсказуемые входные данные и мы работаем с компьютером, у которого арифметика с плавающей точкой подвержена погрешностям. Если нужна скорость и качество совершенно неважно – трассировка лучей в помощь. В большинстве реальных приложений скорее всего поможет метод ближней точки и нормали. Если же на первом месте – точность определения при непонятных входных данных, метод индекса точки должен помочь.

Если будут какие-то вопросы, задавайте. Как человек, занимающийся геометрией и подобными проблемами связанными с графикой, буду рад помочь чем смогу.