Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем
Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
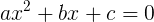
Перейдем от квадратного уравнения к квадратичной функции:
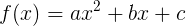
Где, очевидно, необходимо найти такие значения аргумента
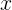функции, в которых оная возвратила бы ноль.Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант. Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!
Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент
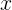в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.Что же дальше делать? Непонятно. А в любом непонятном случае нужно брать производную ещё раз:
На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси
при искомом движении:
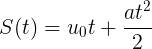
Где
— время,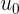 
— начальная скорость, 
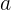— ускорение.Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.
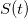можно найти площадь фигуры. Там вылезет трапеция.Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Теперь осталось разобраться что есть что, и чего нам не хватает.
«Ускорение»
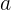у нас уже есть — им является производная второго порядка 
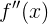, выведенная выше. А вот чтобы получить начальную скорость 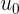, нам нужно взять в общем-то любой 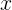(обозначим его как 
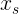) и подставить его в производную теперь уже первого порядка 
— ибо она и будет искомым.В таком случае возникает вопрос, какой же
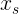нужно взять? Очевидно, такой, чтобы начальная скорость 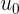была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:
В таком случае составим уравнение для поиска
:
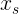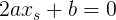[подставили 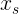в производную первого порядка ]Корнем такого уравнения относительно
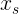будет:
А значением исходной функции
при таком аргументе будет:
Вспомним, какой целью мы задались в самом начале: «необходимо найти такие значения аргумента
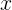функции, в которых оная возвратила бы ноль». Иными словами, нам от положения 
необходимо «дойти до нуля».Так как теперь нам известна начальная скорость, ускорение и какой путь необходимо пройти, то настало время отметить следующее:
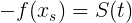, также как и 
Тогда, подставив все известные величины, получим:
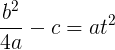
Поделим все на
:
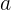Теперь становится очевидно, что:
Соединим все «детали пазла» воедино:
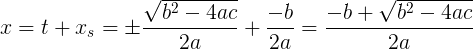
Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.
С вами был Петр, спасибо за внимание!
Комментарии (23)
Amareis
21.06.2016 12:29+1А как выводится эта формула не окольными путями?
ParadoxFilm
21.06.2016 13:11Действительно, самый простой способ — с помощью «формул сокращенного умножения»:
kahi4
21.06.2016 13:43+7Мне кажется, или вы вывели формулу через ее саму же… странное чувство.
Также нельзя оставлять без внимания тот факт, что формула для РУД выше по факту есть результат взятия интеграла от формулы скорости такого движения.
Чтобы эта формула стала интегралом, ей не хватает неизвестной константы.ParadoxFilm
21.06.2016 16:11Неизвестная константа — это
, и в данном случае она равна нулю (т.к. это перемещение по оси OX). P.S. Можно взять интеграл от формулы скорости при ПРУД. Или из графика найти площадь фигуры. Там вылезет трапеция.
Или вообще можно так.
Этим мы показываем, что формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Спасибо за внимание!
Jamdaze
21.06.2016 16:13-3Всегда было интересно зачем в школе пичкают этими уравнениями. За 30 лет жизни они мне ниразу не пригодились, даже косвенно.
Может кто знает где применяются квадратные уровнения?ParadoxFilm
21.06.2016 16:15+1«Математику только затем учить надо, что она ум в порядок приводит» (М. В. Ломоносов).
А вот «пичкать» действительно не надо.
lorc
21.06.2016 20:14Там где есть квадратичные зависимости, очевидно. Например — в школьной физике их хватает. Или физика тоже не нужна?
А ещё квадратные уравнения подготавливают к знакомству с полиномами более высоких порядков. Которые используются да хоть в той же интерполяции сплайнами.
А косвенно вы решаете эту задачу каждый раз, когда прикидываете, успеет ли затормозить машина перед вами.
DrNefario
21.06.2016 22:29-1Они негде не применяются сами по себе. Они возникают при построении математических моделей, коих решить вам предстоит для получения результата. И чтобы постоянно не перевыводить все, люди фиксируют формулы/алгоритмы решения. Все ради скорости. Время — самый ценный ресурс.
pchelintsev_an
24.06.2016 19:16Геометрическая задача. Заданы координаты центра круга и его радиус. Также дана точка A вне этого круга. Найти уравнения касательных и угол alpha между ними, проведенных из точки A к кругу. Эта задача может иметь и практическое применение (поиск угла обзора alpha).
saluev
22.06.2016 11:36Например, нужно решить квадратное уравнение, чтобы найти пересечение окружности с отрезком. Будете писать 2D-игру с физикой — без квадратных уравнений не обойдётесь.
pchelintsev_an
24.06.2016 16:16Например, при построении решений некоторых обыкновенных линейных дифференциальных уравнений (решение характеристического уравнения), а такие уравнения часто возникают в инженерных приложениях.
pchelintsev_an
24.06.2016 18:11У Я.И. Перельмана в его книге «Занимательная алгебра» есть задача о громкоговорителях (стр. 140-141), решение которой сводится к квадратному уравнению:
На площади установлено 13 громкоговорителей, разбитых на две группы: в одной 4, в другой 9 аппаратов (от себя: то есть громкоговорители висят на двух столбах). Расстояние между группами 50 м. Где надо стать, чтобы звуки обеих групп доносились с одинаковой силой?
pchelintsev_an
24.06.2016 18:49Ещё пример — задача на экстремум. Требуется при заданных издержках (суммарные затраты производства b = c1 * x1 + c2 * x2) определить количества x1 и x2 факторов производства (то есть затраты определенных продуктов в количествах x1 >= 0 и x2 >= 0, с1 и c2 — их цены за единицу), которые максимизируют объём продукции f(x1, x2). Можно задать такой вид функции f, что решение данной экономической задачи сведётся к квадратному уравнению.
saluev
<Как мог бы выглядеть вывод формулы для дискриминанта в XVII веке>.
lorc
В том то и дело, что нет. Квадратные уравнения решали ещё в древнем Вавилоне. А диференциальное счисление придумали Нютон с Лейбницем не так давно.