
Перевод поста Стивена Вольфрама "What Is Spacetime, Really?".
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации.
Примечание: данный пост Стивена Вольфрама неразрывно связан с теорией клеточных автоматов и других смежных понятий, а также с его книгой A New Kind of Science (Новый вид науки), на которую из этой статьи идёт большое количество ссылок. Пост хорошо иллюстрирует применение программирования в научной сфере, в частности, Стивен показывает (код приводится в книге) множество примеров программирования на языке Wolfram Language в области физики, математики, теории вычислимости, дискретных систем и др.
Содержание
Простая теория всего?
Структура данных Вселенной
Пространство как граф
Может быть, нет ничего, кроме пространства
Что есть время?
Формирование сети
Вывод СТО
Вывод ОТО (Общей теории относительности)
Частицы, квантовая механика и прочее
В поисках вселенной
Ок, покажите мне Вселенную
Заниматься физикой или нет — вот в чем вопрос
Что требуется?
Но пришло ли время?
Сто лет назад Альберт Эйнштейн опубликовал общую теорию относительности — блестящую, элегантную теорию, которая пережила целый век и открыла единственный успешный путь к описанию пространства-времени (пространственно-временного континуума).
Есть много различных моментов в теории, указывающих, что общая теория относительности — не последняя точка в истории о пространстве-времени. И в самом деле, пускай мне нравится ОТО как абстрактная теория, однако я пришел к мысли, что она, возможно, на целый век увела нас от пути познания истинной природы пространства и времени.
Я размышлял об устройстве пространства и времени немногим более сорока лет. В начале, будучи молодым физиком-теоретиком, я просто принимал эйнштейновскую математическую постановку задачи специальной и общей теории относительности, а так же занимался некоторой работой в квантовой теории поля, космологии и других областях, основываясь на ней.
Но около 35 лет назад, отчасти вдохновленный своим опытом в технических областях, я начал более детально исследовать фундаментальные вопросы теоретической науки, с чего и начался мой длинный путь выхода за рамки традиционных математических уравнений и использования вместо них вычислений и программ как основных моделей в науке. Вскоре после этого мне довелось выяснить, что даже очень простые программы могут демонстрировать очень сложное поведение, а затем, спустя годы, я обнаружил, что системы любого вида могут быть представлены в терминах этих программ.
Воодушевившись этим успехом, я стал размышлять, может ли это иметь отношение к важнейшему из научных вопросов — физической теории всего.
Во-первых, такой подход казался не слишком перспективным — хотя бы потому, что модели, которые я изучал (клеточные автоматы), казалось, работали так, что это полностью противоречило всему тому, что я знал из физики. Но где-то в 88-м году — в то время, когда вышла первая версия Mathematica, я начал понимать, что если бы я изменил свои представления о пространстве и времени, возможно, это к чему то бы меня привело.
Простая теория всего?
Из статьи вовсе не кажется очевидным, что теория всего для нашей вселенной должна быть проста. И в самом деле, история физики привносит дополнительные сомнения, ведь чем больше мы узнаем, тем вещи оказываются более сложными, во всяком случае, в терминах математического аппарата, вводимого ими. Но, как отмечалось, к примеру, богословами много веков назад, есть очевидная черта нашей вселенной — в ней есть порядок. Частицы нашей вселенной не просто подчиняются каким-то своим законам, но и подчиняются определённому набору общих законов.
Но насколько простой может быть теория всего для нашей Вселенной? Скажем, мы можем представить её в виде программы, допустим, в Wolfram Language. Насколько большой будет эта программа? Будет ли оно сравнима с длиной человеческого генома, или больше походить по объему на операционную систему? Или же она будет значительно меньше?
Если бы я отвечал на этот вопрос до того, как начал исследовать вычислительную вселенную простых программ, я бы, скорее всего, ответил, что подобная программа должна быть чем то весьма сложным. Однако мне удалось обнаружить, что в вычислительной вселенной даже чрезвычайно простые программы могут демонстрировать сколь угодно сложное поведение (этот факт отражен в общем принципе вычислительной эквивалентности).

Структура данных Вселенной
Но какой должна быть такая программа? Ясно одно: если программа и вправду может быть чрезвычайно простой, то она будет слишком мала для того, чтобы в явной форме кодировать некоторые очевидные особенности нашей Вселенной, такие как массы частиц, разного рода симметрию, или даже пространственную размерность. Все эти вещи должны появляться каким-то образом из чего-то более низкоуровневого и фундаментального.
Но если поведение вселенной определяются простой программой, то какова структура данных, с которыми эта программа работает? Сперва я предположил, что это должно быть нечто простое для описания, как, к примеру, структура клеток, которая появляется в клеточном автомате. Но даже если подобная структура хорошо работает для описания моделей различных вещей, представляется, что она должна быть весьма неправдоподобной для фундаментальных физических моделей. Да, можно найти такие правила, что будут демонстрировать поведение, которое в большом масштабе не будет показывать очевидное свойства структуры. Однако если физика действительно может описываться некоторой простой моделью, то представляется, что столь жёсткая структура для пространства не может быть в неё включена, и что свойства пространства должны из чего-то проистекать.
Так какова альтернатива? Нам потребуется более низкоуровневое понятие, чем пространство, из которого оное и будет рождаться. Также нам потребуется базовая структура данных, которая будет максимально гибкой. Я размышлял об этом много лет, изучая самые разнообразные вычислительные и математические формальные системы. Но в конце концов я понял, что по сути все, с чем я сталкивался, может быть представлено одним способом — с помощью сетей.
Сеть — она же граф — состоит из некоторого количества узлов, которые соединены связями. И все свойства графа следуют из структуры этих связей.
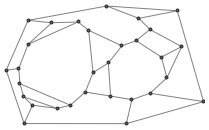
Пространство как граф
Так может ли пространство состоять из чего-то подобного? В классической физике и ОТО пространство не представляется как состоящее из чего бы то ни было. Оно представляется в виде некоторой математической конструкции, которая служит чем-то вроде сцены, на которой имеется непрерывный диапазон возможных положений, занимаемых разными объектами.
Однако можем ли мы точно сказать, что пространство является непрерывным? Когда квантовая механика зарождалась, была популярна идея о том, что пространство, как и всё остальное, квантуется. Но было не ясно, как эту идею можно сопрячь со СТО, собственно, не было и явных доказательств дискретности пространства. Когда я начал заниматься физикой в семидесятых, обсуждение дискретности пространства сошло на нет, плюс экспериментально было доказано, что в масштабах до 10-18м (1/1000 радиуса протона, или аттометр) дискретности не наблюдается. Спустя 40 лет и десятки миллиардов долларов, потраченные на ускорители частиц, в масштабах до 10-22 м (или 100 йоктометров) дискретность пространства так и не обнаружили.
Однако есть мнение, что она должна проявиться в масштабах около планковской длины — 10-34 метра. Но когда люди размышляют об этом, скажем, в контексте спиновых сетей, петлевой гравитации или чего бы ты ни было, то они склонны предполагать, что всё, что там происходит, тесно связано с формализмами и понятиями квантовой механики.
Но что, если пространство — вероятно, в планковских масштабах — есть лишь старый добрый граф, лишённый квантовых свойств? Звучит не особо впечатляюще, однако для задания подобного графа требуется значительно меньше информации — достаточно просто сказать, какие узлы с какими соединены.
Но как подобное может порождать пространство? Прежде всего, откуда на больших масштабах возникает видимая непрерывность пространства? На самом деле, всё очень даже просто: это может быть следствием большого количество узлов и связей. Немного напоминает то, что происходит в жидкостях — скажем, в воде. В малых масштабах мы можем наблюдать молекулы, мечущиеся в тепловом движении. Однако масштабный эффект заставляет все эти молекулы порождать то, что мы воспринимаем как непрерывную жидкость.
Так получилось, что в середине 80-х я много времени уделял изучению этого феномена — это было частью моей работы, в которой я разбирался в природе кажущейся случайности турбулентных потоков жидкости. В частности, мне удалось показать, что если представить молекулы как клетки клеточного автомата, то их крупномасштабное поведение будет точно описываться дифференциальными уравнениями для потоков жидкости.
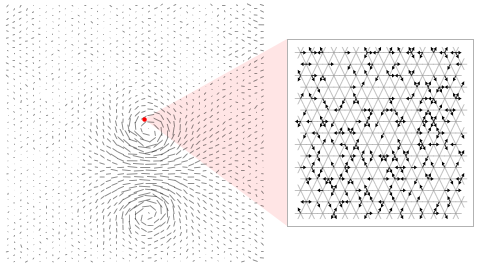
И потому, когда я начал размышлять о возможности существования подструктуры пространства, которое можно представить в виде сети, мне подумалось, что здесь можно использовать те же методы, и что это может свести уравнения ОТО Эйнштейна к другим, существенно более низкоуровневым.
Может быть, нет ничего, кроме пространства
Хорошо. Допустим, пространство есть сеть. Но что можно сказать обо всех вещах, располагаемых в пространстве? Что можно сказать об электронах, кварках, протонах и прочем? Стандартные физические представления говорят о том, что пространство есть сцена, на которой располагаются частицы, струны или что бы то ни было. Однако подобное представление становится весьма сложным. Но есть и более простой вариант: возможно, всё в нашей вселенной состоит из пространства.
В последние годы своей жизни Эйнштейн был весьма увлечен этой идеей. Он полагал, что, быть может, такие частицы, как электроны, можно рассматривать как нечто вроде черных дыр, что состоят из одного лишь пространства. Однако, опираясь лишь на формализм ОТО, Эйнштейн не смог развить эту идею, в результате чего она была заброшена.
И, так уж было, что за сотню лет до этого в умах некоторых людей жили подобные идеи. Это были времена до СТО, когда люди думали, что пространство заполнено средой, подобной жидкости — эфиром (по иронии судьбы в настоящее время мы вернулись к модели заполненного пространства — полем Хиггса, квантовыми флуктуациями в вакууме и прочим). Между тем, было понятно, что существуют различные типы атомов, соответствующие различным химическим элементам. И было выдвинуто предположение (в частности, Кельвином), что разным атомам можно сопоставить различные узлы эфира.
Это интересная идея, хоть и неправильная. Но, представляя пространство как сеть, можно рассмотреть схожую идею: возможно, частицы соответствуют определенным структурам сети. Быть может, всё сущее во вселенной есть сеть, а материи соответствуют какие-то структуры этой сети. Подобные вещи легко можно обнаружить на поле клеточного автомата. Даже если каждая клетка подчиняется некоторым простым правилам, в системе появляются определенные структуры со своими свойствами — прямо как частицы с физикой взаимодействия друг с другом.

То, как всё это может реализовываться на сетях — отдельная и очень большая тема. Однако сперва нам стоит обсудить одну очень важную вещь — время.
Что есть время?
В 19-ом веке были понятия пространства и времени. Оба описывались координатами, а с помощью некоторых математических формализмов появлялись схожим путем. Однако мысль о том, что пространство и время в некотором роде есть одно и то же, не была в ходу. Но потом появился Эйнштейн с ОТО, и люди начали говорить о пространстве-времени, в котором пространство и время есть грани некоего единого понятия.
Оно вносит множество смыслов в СТО, в которой, к примеру, перемещение с переменной скоростью есть суть вращение в четырехмерном пространстве-времени. И весь этот век физики полагали пространство-время некоей сущностью, в которой пространство и время не имеют фундаментальных различий.
Но как всё это будет работать в контексте сетевой модели пространства? Конечно, можно ввести четырёхмерную сеть, в которой время будет работать так же, как и пространство. А потом просто сказать, что нашей вселенной соответствует некоторая пространственно-временная сеть (или семейство сетей). Каждая сеть должна определяться некоторыми ограничениями: наша вселенная обладает такими и такими свойствами, и, получается, удовлетворяет таким и таким уравнениям. Однако это представляется неконструктивным подходом — он не говорит о том, как вселенная ведет себя, а лишь о том, что если что-то обладает таким-то поведением, то это что-то может быть вселенной.
И, к примеру, в контексте программ пространство и время проявляются весьма по-разному. В клеточных автоматах, к примеру, клетки располагаются в пространстве, однако поведение системы возникает в пошаговых изменениях времени. Но вот какой момент: из того, что низкоуровневые правила сильно разграничивают поведения пространства и времени, не следует, что на больших масштабах они не будут вести себя схожим образом — как и полагается в современной физике.
Формирование сети
Итак, давайте предположим, что сеть есть подпространственная структура. Как эта сеть формируется? Можно ввести простую гипотезу, которая заключается в том, что существует некое местное правило, которое говорит, что если вы видите некоторый фрагмент сети, выглядящий некоторым образом, то его следует заменить на фрагмент, который выглядит так.

Но теперь все становится немного сложнее. Ведь может быть много мест в сети, где можно применить подобное правило. Так что определяет порядок обработки каждого фрагмента?
По сути, каждое возможное упорядочение соответствует своему временному потоку. И можно было бы вообразить теорию, в которой все потоки имеют место быть, и наша вселенная имеет множественную историю.
Но мы можем обойтись и без этой гипотезы. Вместо этого, вполне возможно, существует лишь одна нить времени — и это хорошо соотносится с тем, что мы знаем о мире, с нашим опытом. И чтобы понять это, нам следует сделать нечто наподобие того, что сделал Эйнштейн, формулируя СТО: нам следует ввести более реалистичную модель того, чем может являться наблюдатель.
Излишне говорить, что какой-либо реальный наблюдатель должен иметь возможность существовать в нашей вселенной. Таким образом, если вселенная представляет собой сеть, то наблюдатель должен быть некоей частью этой сети. Вспомним теперь о постоянных небольших изменениях, которые происходят в сети. Чтобы знать, что подобное изменение (обновление) произошло, наблюдатель и сам должен быть изменен (обновлен).
Если вы проведете всю эту мысленную цепочку, которую я провел в книге A New Kind of Science (NKS), то поймете, что единственное, что могут воспринимать наблюдатели в истории вселенной — причинную сеть — то, когда одно событие вызывает другое.
А потом выясняется, что есть определенный класс базисных правил, для которых различные порядки базисных обновлений не влияют на причинно-следственную сеть. Их я называю «причинно-следственно инвариантными» правилами.
Причинная инвариантность является интересным свойством, которое имеет аналоги в различных вычислительных и математических системах, например в том, что преобразования в алгебре могут быть применены в любом порядке и будут давать один и тот же конечный результат. Но в контексте вселенной его следствием является то, что он гарантирует, что есть только один поток времени во вселенной.
Вывод СТО
Так что насчёт пространства-времени и СТО? Тут, как я понял в середине 90-х, происходит нечто захватывающее: если есть причинно-следственная инвариантность, то из этого следует, что на больших масштабах СТО будет появляться сама собой. Другими словами, даже если на самом низком уровне пространства и времени всё происходит совсем по-другому, то в большем масштабе всё это порождает то, что предписывает СТО.
Грубо говоря, системы отсчета в специальной теории относительности — связанные, например, с перемещениями при разных скоростях — соответствуют различным последовательностям низкоуровневых изменений сети. Но из-за причинной инвариантности общее поведение, ассоциированное с различными последовательностями, получается точно таким-же — таким образом, система удовлетворяет принципам СТО.
В начале данная ситуация могла бы показаться безнадежной: как может сеть, которая рассматривает пространство и время по-разному, сойтись со СТО? Но это работает. И в самом деле, я не знаю никакой другой модели, которая может успешно вывести принципы СТО из чего-то более низкоуровневого; в современной физике это всегда представлялось как данность.
Вывод ОТО (Общей теории относительности)
Ок, СТО можно получить из простых моделей, основанных на сетях. Но что можно сказать об ОТО? Есть очень хорошая новость: опираясь на различные предположения, в конце 90-х мне удалось вывести уравнения Эйнштейна из динамики сетей.
Вся эта история в действительности несколько сложнее, но вот примерный пересказ. Во-первых, нам стоит вообразить, как сеть формирует из себя пространство. Следует помнить, что сеть есть лишь набор узлов и связей. Притом узлы могут располагаться в одномерном, двумерном или любом n-мерном пространстве.
Легко увидеть, что есть сети, которые в больших масштабах представляются двумерными или трехмерными. На самом деле, есть простой тест для определения эффективной размерности сети. Возьмем некоторый узел, а затем посмотрим на все узлы, отстоящие от него на r связей. Если сеть проявляет себя как d-мерная, то число узлов в этой «сфере» будет около rd.
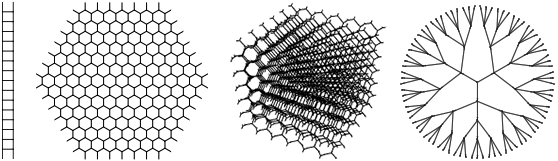
И тут вещи приобретают интересный оборот. Если сеть ведет себя как неискаженное в пространстве большей размерности d-мерное пространство, то число узлов всегда будет около rd. Но если поведение подобно искривленному пространству (как в ОТО), то будет иметь место поправочный член, пропорциональный такому математическому объекту, как тензор Риччи. И это весьма интересно, ведь тензор Риччи как раз и возникает в уравнениях Эйнштейна.
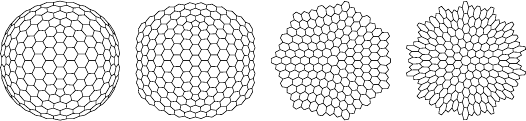
Тут много математических сложностей. Следует рассмотреть кратчайшие пути — геодезические линии сети. Следует понять, как сделать что бы то ни было не только в пространстве, но и на сети с течением времени. Так же следует понять то, до каких масштабов проявляются свойства сети.
При выводе математических результатов важно иметь возможность получать разного рода средние значения. По сути, это подобно выведению уравнений для жидкости из динамики молекул: нужно иметь возможность принимать среднее из некоторого диапазона случайных значений в низкоуровневых взаимодействиях.
Но хорошая новость заключается в том, что существует необъятное количество систем, построенных даже на чрезвычайно простых правилах, которые подобны цифрам числа пи, то есть для любых прикладных целей являются достаточно случайными. Получается, что даже если особенности причинной сети полностью определены для того, кто знает исходное состояние сети, то большая часть этих особенностей будут являться, по сути, случайными.
Вот что имеем в итоге. Если ввести предположение об эффективной микроскопической случайности и предположить, что поведение системы в целом не приводит к изменению во всех ограничивающих размерностях, то из этого следует, что масштабное поведение системы удовлетворяет уравнениям Эйнштейна!
Полагаю, это очень интересно. Уравнения Эйнштейна можно получить практически из ничего. Это означает, что эти простые сети воспроизводят черты гравитации, которые мы знаем из современной физики.
Есть ряд деталей, которые не подходят под формат этой статьи. Многие из них я озвучивал довольно давно в NKS, особенно в заметках в конце.
Некоторые из вещей, возможно, стоит упомянуть. Во-первых, стоит отметить, что эти базисные сети не только представляются в обычном непрерывно определенном пространстве, но и не определяют такие топологические понятия, как внутри и снаружи. Все эти понятия являются следствием и выводятся.
Когда дело доходит до вывода уравнений Эйнштейна, тензоры Риччи рождаются из геодезических линий на сети вместе с ростом сфер, которые берут начало из каждой точки на геодезической линии.
Полученные уравнения Эйнштейна являются уравнениями Эйнштейна для вакуума. Но как и в случае с гравитационными волнами, можно эффективно отделить особенности пространства, связанные с материей, а затем получить полные уравнения Эйнштейна в терминах материи-энергии-импульса.
Когда я пишу это, то понимаю, насколько легко скатываюсь к «языку физиков» (вероятно, это связано с тем, что я занимался физикой в молодости...). Но достаточно просто сказать, что на высоком уровне появляется захватывающая вещь, которая заключается в том, что из простой идеи о сетях и причинно-следственно инвариантных правил замены можно вывести уравнения ОТО. Сделав удивительно мало, мы получаем яркую звезду физики 20-го века: общую теорию относительности.
Частицы, квантовая механика и прочее
Весьма здорово — иметь возможность вывести ОТО. Но на этом физика не заканчивается. Другой очень важной её частью является квантовая механика. Боюсь, я не смогу в рамках этой статьи подробно развернуть эту тему, но, по-видимому, такие частицы, как электроны, кварки или бозоны Хиггса должны представляться в виде некоторых особых областей сети. В качественном смысле они могут не сильно отличаться от «эфирных узлов» Кельвина.
Но тогда их поведение должно следовать правилам, которые мы знаем из квантовой механики — или, если более конкретно — из квантовой теории поля. Ключевой особенностью квантовой механики является то, что она может быть сформулирована в терминах множественных поведений, каждое из которых связано с определенной квантовой амплитудой. Я не до конца со всем этим разобрался, однако есть намек на то, что нечто подобное происходит, если смотреть на эволюцию сети с различными возможными последовательностями низкоуровневых замен.
Моя сетевая модель, говоря строго, не имеет никаких квантовых амплитуд. Она больше похожа (но не в точности) на классическую, по сути, вероятностную модель. И в течение полувека люди считали, что с подобными моделями сопряжены практически нерешаемые проблемы. Ведь есть такая теорема Белла, в которой говориться, что если нет мгновенных нелокальных распространений информации, то не найдется и такой модели «скрытых переменных», что сможет воспроизвести квантово-механические результаты, наблюдаемые экспериментально.
Но есть принципиальные замечания. Вполне себе ясно, что означает нелокальность в обычном пространстве некоторой размерности. Но что можно сказать в контексте сетей? Тут всё по-другому. Потому что все определяется одними лишь связями. И хоть сеть и может в больших масштабах представляться трехмерной, остаётся возможность, что есть некие «нити», соединяющие некоторые области, которые без оных были бы отделены друг от друга. И мне не даёт покоя одна мысль — есть основания полагать, что эти нити могут генерироваться подобными частицам структурами, распространяющимися в сети.
В поисках вселенной
Хорошо, получается, что некоторые модели на основе сетей могут воспроизвести модели современной физики. Но с чего стоит начать поиск модели, в точности воспроизводящей нашу вселенную?
Первая мысль — начать с существующей физики и попытаться адаптировать инженерно-прикладные правила так, чтобы воспроизвести её. Но единственный ли это путь? А что если просто начать перечислять все возможные правила, ища среди них те, что будут описывать нашу вселенную?
Не начав изучение вычислительной вселенной простейших программ, я бы подумал, что это безумная затея: правила нашей вселенной никак не могут быть достаточно простыми для того, чтобы их можно было бы найти простым перечислением. Но увидев, что творится в вычислительной вселенной и увидев некоторые другие примеры, в которых потрясающие вещи были найдены одним лишь перебором, я понял, что ошибаюсь.
Но что будет, если кто-то действительно начнет осуществлять подобный поиск? Вот подборка сетей, полученных после довольно небольшого числа шагов, используя все возможные правила определенного, весьма простого типа:
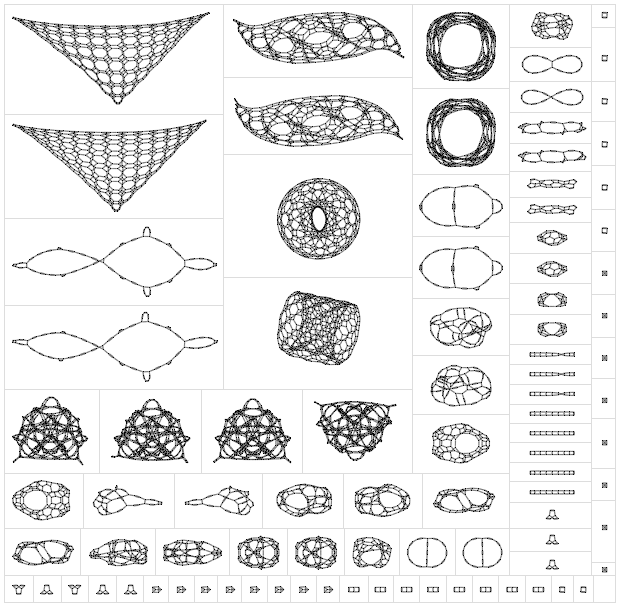
Некоторые из этих сетей явно не соответствуют нашей вселенной. Они просто замирали спустя несколько итераций, то есть время в них, по сути, останавливалось. Или структура их пространства была слишком простой. Или у них было бесконечное число измерений. Или какие-то другие проблемы.
Здорово, что с такой удивительной быстротой мы можем найти те правила, которые явно не соответствуют нашей вселенной. А сказать то, что именно этот объект — наша вселенная, является значительно более сложной задачей. Потому что даже если смоделировать большое количество шагов, то невероятно сложно будет показать то, что поведение этой системы демонстрирует то же самое, что говорят нам физические законы о ранних моментах жизни вселенной.
Хотя есть ряд обнадеживающих вещей. Например, эти вселенные могут рождаться с фактически бесконечным числом измерений, а затем постепенно сжиматься до конечного числа измерений, потенциально устраняя необходимость в явной инфляции в ранней Вселенной.
А если рассуждать на более высоком уровне, то следует помнить, что если использовать весьма простые модели, то будет иметь место большое расстояние между «соседними моделями», так что, скорее всего, эти модели будут либо точно воспроизводить известные физические построения, либо будут далеки от истины.
В конце концов, нужно воспроизвести не только правила, но и начальное состояние вселенной. И как только мы узнаем его, то мы принципиально сможем узнать точную эволюцию вселенной. Так означает ли это, что можно было бы сразу узнать все о вселенной? Однозначно нет. Из-за явления, которое я называю «вычислительной несводимостью», и которое подразумевает, что если знать правила и начальное состояние для системы, она по-прежнему может требовать неприводимое количество вычислительной работы для прослеживания каждого шага системы в выяснения того, что она делает.
Тем не менее, существует вероятность, что кто-то сможет найти простое правило и начальное состояние, сказав: "Смотрите-ка, это наша вселенная!" Мы нашли бы нашу вселенную в пространстве всех возможных вселенных.
Конечно, это было бы знаменательным днём для науки.
Но возникло бы множество других вопросов. Почему именно это правило, а не другое? И почему наша Вселенная должна иметь правило, которое появляется достаточно рано в нашем списке всех возможных вселенных, и которое мы можем найти простым перечислением?
Можно было бы подумать, что именно особенности нашей вселенной и тот факт, что мы в ней находимся, заставят нас сформировать правила перечисления так, что вселенная появится достаточно рано. Но в настоящее время я полагаю, что всё должно быть значительно более экстравагантно, как, например, в случае с наблюдателем во вселенной — все из большого класса нетривиальных возможных правил для вселенных в действительности эквивалентны, потому можно выбрать любое из них и получить точно такие же результаты, просто по-другому.
Ок, покажите мне Вселенную
Но всё это лишь догадки. И пока мы и в самом деле не найдем кандидата на правило нашей вселенной, вероятно, на обсуждение этих вещей не стоит тратить много времени.
Так, хорошо. Какова наша текущая позиция во всем этом? Большую часть из того, что сейчас обсуждалось, я понял где-то в 99-ом — за несколько лет до окончания A New Kind of Science. И хоть я и писал на простом языке, а не в формате статьи по физике, мне удалось покрыть основные моменты этой темы в девятой главе книги, добавив некоторые технические детали в примечаниях в конце.

Но после того, как в 2002 году книга была закончена, я снова начал работать над физическими проблемами. Будет забавным сказать, что в моём подвале стоял компьютер, который искал фундаментальную физическую теорию. Но вот что на самом деле он делал: перечислял возможные правила различных типов и пытался обнаружить соответствие их поведения определенным критериям, которые могли бы сделать их правдоподобными в качестве моделей физики.
Я весьма скрупулёзно проделывал это работу, черпая идеи из простых случаев, последовательно продвигаясь к более реалистичным. Было много технических вопросов. Как представлять большие эфолюционирующие последовательности графов. Или как быстро распознавать слабоуловимые закономерности, которые показывают, что правило не соответствует нашей вселенной.
Работа разрослась на тысячи страниц, если её представлять в печатной форме, постепенно приближая к пониманию основ того, что могут делать системы, основанные на сетях.

В некотором смысле это было чем-то вроде хобби, которым я занимался параллельно с текучкой по управлению компанией и ее технологическим развитием. И был еще один отвлекающий фактор. В течение многих лет я занимался проблемой вычислительных знаний и построением движка, который мог бы всесторонне их реализовывать. И по результатам моей работы над A New Kind of Science я убедился, что это возможно, и что сейчас подходящее время для реализации этого.
К 2005 году стало ясно, что это действительно возможно реализовать, и потому я решил посвятить себя этому направлению. В результате получилась Wolfram|Alpha. И как только Wolfram|Alpha была запущена, то стало ясно, что можно сделать значительно большее — и я посвятил своё, пожалуй, наиболее продуктивное десятилетие на создание огромной системы из идей и технологий, которая дала возможность реализовать Wolfram Language в его нынешнем виде, а так же множество других вещей.
Заниматься физикой или нет — вот в чем вопрос
Но в течение этого десятилетия я не занимался физикой. И когда сейчас я смотрю на файловую систему на своем компьютере, я вижу большое количество ноутбуков с материалами по физике, сгруппированные с полученными мною результатами, и все это оставалось брошенным и нетронутым с начала 2005 года.
Должен ли я вернуться к вопросам физики? Я определенно хочу этого. Хотя есть и другие вещи, которые я хотел бы реализовать.
Я провел большую часть своей жизни, работая над очень большими проектами. И я упорно трудился, планируя то, что собираюсь сделать, пытаясь их распланировать на ближайшее десятилетие. Иногда я откладывал проекты, потому что существующие на тот момент технологии или инфраструктура были ещё не готовы к ним. Но как только я приступал к работе над проектом, я давал себе обещание найти способ его успешно завершить, даже если для его реализации потребуется много лет напряженной работы.
Однако поиск фундаментальной физической теории, пожалуй, несколько отличается от проектов, над которыми мне приходилось работать раньше. В некотором смысле критерии его успеха гораздо жестче: он или решает проблему и находит теорию, или нет. Да, можно было бы найти множество интересных абстрактных понятий из формирующийся теории (как в теории струн). И вполне вероятно, что такое исследование даст интересные побочные результаты.
Но в отличие от создания технологий или исследования научных областей, формулирование содержания этого проекта вне нашего контроля. Его содержание определяется нашей вселенной. И, вполне возможно, я просто ошибаюсь в предположениях о том, как работает наша вселенная. Или, быть может, что я прав, но есть практически непреодолимый барьер из-за вычислительной несводимости, который лишает нас возможностей познать эту сферу.
Кто-то может сказать, что есть вероятность того, что мы найдем некоторую вселенную, которая будет походить на нашу, но мы так никогда и не узнаем, наша ли она в действительности. Я, на самом деле, не особо беспокоюсь об этом. Я думаю, что есть достаточное количество аномалий в существующей физике, приписываемых таким вещам, как темная материя, объяснение которых даст нам полную уверенность в том, что мы нашли верную теорию. Будет здорово, если можно будет сделать предположение и быстро проверить его. Но к тому времени, как мы выведем все, казалось бы, произвольные массы частиц, и другие известные особенности физики, можно будет быть уверенным, что мы имеем дело с верной теорией.
Было занятно в течение многих лет спрашивать у своих друзей, должен ли я заниматься фундаментальными вопросами физики. И получал я три совершенно разных типа ответов.
Первый — простой: "Ты должен заниматься этим!" Они говорили, что проект является самым увлекательным и важным из тех, что можно себе вообразить, и не могут понять, зачем ждать ещё хоть один лишний день, прежде чем к нему приступить.
Второй тип ответов: "Зачем тебе этим заниматься?" Затем они говорят нечто вроде «Почему бы не решить проблему искусственного интеллекта, или молекулярной инженерии, биологического бессмертия, или, по крайней мере, не построить огромную многомиллиардную компанию? Зачем заниматься чем-то столь абстрактным и теоретическим, когда можно сделать что-то насущное и изменить тем самым мир?»
А есть третий тип ответов — весьма ожидаемый, если иметь в виду историю науки. В основном он исходит от моих друзей-физиков, и это некая комбинация из "Не трать своё время на это!" и "Пожалуйста, не надо этим заниматься".
Дело в том, что нынешний подход к фундаментальной физике, основанный на теории квантового поля, насчитывает почти 90 лет. Он имел ряд успехов, однако не привел нас к фундаментальной физической теории. Но для большинства современных физиков нынешний подход и есть суть сама физика. И когда они слышат о том, над чем я работаю, им это кажется чем-то столь незнакомым, будто это на самом деле и не физика.
И некоторые из моих друзей прямо так и говорят: "Я надеюсь, что у тебя ничего не получится, потому что тогда все, над чем я работал, пойдет коту под хвост". Ну, да, многое из сделанного окажется бессмысленным. Но вы всегда сталкиваетесь с этим риском, когда занимаетесь проектом, в котором природа решает что верно, а что нет. Но я должен сказать, что даже если можно будет найти по-настоящему фундаментальную физическую теорию, то останется ещё очень большое поле для работы квантовой теории поля, к примеру — объяснение различных эффектов на масштабах, с которыми мы работаем в настоящее время на ускорителях частиц.
Что требуется?
Так, хорошо, если я запущу проект по поиску фундаментальной физической теории, то что мне следует делать? Это сложный проект, которому потребуюсь не только я, но также и разнородная группа талантливых людей.
Будет ли он в конечном счете работать — не знаю, но думаю, что будет довольно интересно за ним наблюдать, и я планирую представить его в прозрачном формате, сделав его максимально доступным и познавательным (конечно, это будет ободряющим контрастом с тем режимом отшельника, в котором я работал над A New Kind of Science в течение десяти лет).
Безусловно, я не могу знать, насколько сложен этот проект, и принесет ли он вообще результаты. В конечном счете это зависит от того, какова есть на самом деле наша вселенная. Но, основываясь на том, что я сделал десять лет назад, у меня есть четкий план относительно того, с чего начать и каких людей свести вместе в рамках одной команды.
Тут потребуются как хорошие учёные, так и прикладники/инженеры. Потребуется проделать много работы в области разработки алгоритмов эволюции сетей и их анализа. Я уверен, что тут потребуется теория графов, современная геометрия, теория групп и, возможно, некоторые другие разделы абстрактной алгебры. И я не удивлюсь, если в итоге будут задействовано большое количество других областей математики и теоретической информатики.
Тут потребуется сложная и серьёзная физика, с понимаем основ квантовой теории поля, теории струн и, возможно, таких разделов, как спиновые сети. Также, вероятно, потребуются методы статистической физики и её современных теоретических основ. Потребуется понимание общей теории относительности и космологии. И, если дела идут хорошо, потребуется работа над большим количеством разнообразных физических экспериментов, а также их интерпретация.
Будут и технические проблемы — понять, к примеру, то, как проводить огромную вычислительную работу по сетям и визуализировать получаемые результаты. Но я подозреваю, что самые большие проблемы будут в строительстве здания новой теории и понимании того, что необходимо для изучения различных видов сетевых систем, которые я хочу исследовать. Будет не лишней поддержка из существующих ныне областей. Но, в конце концов, подозреваю, потребуется построение существенно новой интеллектуальной структуры, которая не будет похожа ни на что из того, что имеется сейчас.
Но пришло ли время?
Подходящее ли сейчас время для реализации подобного проекта? Может быть, следует подождать, пока компьютеры получат больше вычислительных возможностей. Или когда некоторые области математики продвинутся дальше. Или пока не будут получены ответы на еще несколько вопросов из физики.
Я не уверен. Но я и не вижу никаких непреодолимых препятствий, а лишь то, что на этот проект потребуются усилия и ресурсы. И кто знает: может быть, это окажется проще, чем мы думаем, и мы, оглядываясь назад, будем задаваться вопросом — почему этого никто не сделал ранее.
Одним из ключевых моментов, который привел к общей теории относительности 100 лет назад, заключался в том, что пятый постулат Евклида («параллельные линии никогда не пересекаются») может и не выполняться в реальной вселенной, давая возможность существования искривленного пространства. Но если мои подозрения о космосе и вселенной верны, то это означает, что на самом деле есть и более фундаментальная проблема в основаниях Евклида — в самых первых его определениях. Ведь если существует дискретная подпространственная сеть, то предположения Евклида о точках и линиях, которые могут занимать любые пространственные положения, попросту не верны.
ОТО — отличная теория, но мы уже знаем, что она не может быть окончательной. И теперь мы должны задаться вопросом — сколько пройдет времени, прежде чем мы придем к окончательной теории. Надеюсь, не слишком много. И я надеюсь, что ОТО отпразднует не слишком много юбилеев прежде, чем мы узнаем, что же есть пространство-время на самом деле.
Комментарии (137)
dimkss
22.06.2016 14:41Добавить бы номера к абзацам, для отмечания, когда перестаешь понимать.
И опрос — кто на каком абзаце.
(Спасибо за статью. Очень интересно)
tmnhy
22.06.2016 15:12ЯННП
Можно ввести простую гипотезу, которая заключается в том, что существует некое местное правило, которое говорит, что если вы видите некоторый фрагмент сети, выглядящий некоторым образом, то его следует заменить на фрагмент, который выглядит так "скан с геометрическими фигурами".
И из этого выводится сначала СТО, а потом и ОТО. Мне одному непонятно как и почему?
OsipovRoman
22.06.2016 15:19Подробнее Стивен описывает это в книге.

locutus
24.06.2016 12:51Простите, но там нет никакой СТО или теории гравитации. Только общие пространные рассуждения и красивые картинки. В других главах, которые касаются физики, тоже.
Простите, это философская работа, построенная на базе неоплатонизма. Платоники, на мой взгляд, делают крупную ошибку, когда символы нашего языка — объекты, формулы, чертежи — объявляют физической реальностью. Природа не обязана им следовать.
И да, полевой подход работает и пока что не видно причин тому, почему он не будет работать в дальнейшем.

leshabirukov
22.06.2016 15:47Пространство как граф
Интереснее, как возникает изотропия, принцип относительности Галилея например.
Прежде всего, откуда на больших масштабах возникает видимая непрерывность пространства?
Вместо этого, вполне возможно, существует лишь одна нить времени — и это хорошо соотносится с тем, что мы знаем о мире, с нашим опытом.
Вполне возможно, существует только один человек — и это хорошо соотносится с моим самоосознанием.
если есть причинно-следственная инвариантность, то из этого следует, что на больших масштабах СТО будет появляться сама собой.
Ещё нужно как минимум, близкодействие, иначе Ньютон.

Valery35
22.06.2016 15:52Время многомерно :)

snuk182
23.06.2016 10:42а пространство анизотропно. но это еще надо доказать, а потом жить с этим…

locutus
24.06.2016 13:03Эмми Нетёр нарушает теорему об изменении момента количества движения от таких заявлений

snuk182
24.06.2016 15:19Не нашел проверку теоремы на космологических масштабах (> размера галактики).

locutus
24.06.2016 18:49Пока что гравитацию пытаются спасти с помощью темной материи.
А так, т. Нетер это математическое выражение, которое говорит, что если пространство, например, изотропно, то работает определенный закон сохранения. Для математики критерий истинности это не эксперимент, но непротиворечивое доказательство.
snuk182
29.06.2016 23:25Математика уже минимум разок облажалась при описании физических явлений, что привело к теориям относительности и новой, более общей математике. На космологических размерах есть также шансы, что в текущем виде она сломается.

Nekto_Habr
22.06.2016 18:32Ужасно охота ляпнуть чего-то, не имя образования в этом вопросе — уж очень интересная тема… Чёрт с ним:
>>Но что будет, если кто-то действительно начнет осуществлять подобный поиск? Вот подборка сетей, полученных после довольно небольшого числа шагов, используя все возможные правила определенного, весьма простого типа: [картинка сетей]
Что если правило будет такое, что сеть станет фракталом? Время в таком никогда не остановится, т.к. фрактал будет видоизменяться бесконечно.
PS: но я так и не понял, что представляет из себя узел этой сети.
Всё, прошу прощения если кого-то оскорбил вероятной глупостью. Но буду рад дискуссии.
KirillGuzenko
22.06.2016 19:49Думаю, сложно говорить о каких-то представлениях описываемых Стивеном узлов. У них нет даже нет координат, только лишь контекст общей топологии. Суть есть ноумен без чего-бы то ни было феноменального, кроме контекста общей топологи. Но это если говорить о сетях как о реально существующих объектах, а не моделях. Но это не «позитивистично», так сказать.
Если проще: сети — просто математические объекты, и нет смысла говорить о свойствах узлов до тех пор, пока мы сами не присовокупим к ним свойства (к примеру, это может понадобиться, чтобы получить сети какого-то заданного класса).

KonstantinSamsonov
22.06.2016 19:45+3Пространство — это граф, а энергия это его локальная связность, которая не бесконечна, но может быть очень велика, частицы это изменения связности в окрестности, диссипация энергии — это квантованное уменьшение связности графа. Постоянная Планка (10^-34) вполне штучный квант действия или связности. Вакуум — это разрежённый граф со слабой связностью и часто с наведённым нарастанием локальной связности при интерференции мигрирующих связностей через друг друга. На масштабах планковских длин (10^-35) даже размер электрона (10^-15) в этих единицах примерно равен количеству молекул в моле вещества (10^23 против 10^20) что вполне может полностью определить классическую и релятивистскую физику частицы на основе простых правил связности, также как давление выводится из скоростей частиц газа. Нейтрино — это слабоинтерферирующие связности, а скорость света, это 10^44 планковских длин в секунду или один квант связности в один квант времени — предел передачи связности в графе. Хм и потому никаких скоростей выше скорости света.
Стройненько… остаётся только вычислить параметры мощности графа и установить пару правил интерференции одного графа связности на другом или пару десятков…
KirillGuzenko
22.06.2016 19:52Очень интересные мысли, можно их развернуть?

KonstantinSamsonov
22.06.2016 20:45+1Несколько вопросов
Сколько взаимно ортогональных рёбер имеет вершина графа связности?
Как влияет заполнение вершины рёбрами графа на мощность графа и заполнение рёбрами связанных вершин?
Есть ли джиттер на связности ребер ( переключение связности через несколько вершин по разным рёбрам или устойчивые кольцевые колебания количества связей (может быть это спин?, а может ротор этого поля это спин? или кварки с глюонами?)
Как складывать суперпозицию или вычитать или умножать или делить: алгебры и операции над связностями и их множествами
Каково минимальное число связей для устойчивой структуры пространства — для вакуума, для нейтронной материи, для пространства за сферой Шварцшильда?
Возможно ли туннелирование связности через окрестности на размер самой окрестности т.е. при какой связности скорость света преодолевается или же начинается формирование новых вершин, сколько квантов связности тратится на создание новой вершины между двумя окрестностями? Нужна высокая плотность связей или низкая?
Есть ли запрещёные окрестности, окрестности абсолютного отражения связности?
Какой радиус и какую топологию связности имеет электромагнитная волна, электрон ( позитрон скорее всего просто зеркален электрону по ортогональным базисам: т.е. поворотом электрона его не получить и поэтому их интерференция может привести только к двум фотонам и обратно)

KonstantinSamsonov
22.06.2016 20:54https://ru.wikipedia.org/wiki/%D0%9C-%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D1%8F

napa3um
22.06.2016 19:58Ну так любую квантовую теорию можно описать же. Не только соответствующую нашей реальности.

napa3um
22.06.2016 20:04(Но если эти теории можно бы было как-то однозначно пронумеровать и выделить нужный номер теории «нашей» физики или хотя бы описать уравнение, которому должен будет удовлетворять этот номер, Вольфрам бы точно получил нобелевку по физике.)
Cryvage
22.06.2016 19:45Что-то как-то пока никак не воспринимается. Может на выходных удастся въехать. Пока застопорился на графе.

dshuvaev
23.06.2016 00:20Прекрасная идея. Элегантная, интересная, открывающая столько возможностей. И… значит мы все-таки можем быть поключены к матрице.

roller
23.06.2016 02:32Было уже на гиктаймсе же, называлась как то типа «нет причин, по которым наш мир не компьютерная симуляция»
https://geektimes.ru/company/asus/blog/261902/

Sliver
23.06.2016 03:48На сколько я знаю, современная физика не просто не нашла квантов пространства и времени вплоть до 10 ^ -большой степени, но существование этих квантов полностью отрицается современными экспериментами, а это — нечто большее, чем просто «не найдено».
До тех пор, пока с помощью этой теории не будут предсказаны и экспериментально обнаружены какие-то новые эффекты, это будет оставаться прикольной, но бесполезной для практики разминкой для ума.
На сколько я понимаю, пока человек занимается подгонкой своей теории под существующую физику.
Даже если ему удастся сделать это полностью, будет ли эта теория соответствовать действительному устройству Мира? Даст ли она новые результаты?
taujavarob
23.06.2016 17:57Sliver > будет ли эта теория соответствовать действительному устройству Мира?
Действительного устройства Мира не существует. Есть научные парадигмы которые сменяют друг друга по мере смерти их авторов.
Обычным же людям кажется, что они (сменяющие друг друга парадигмы) «расширяют» наше познание какого-то «идеального, действительного, истинного» Мира.

taujavarob
23.06.2016 19:26Sliver > На сколько я знаю, современная физика не просто не нашла квантов пространства и времени вплоть до 10 ^ -большой степени,
Планковская длина примерно 1,6·10?35 метров.
«В настоящее время группа ученых воспользовалась данными съёмки гамма-вспышки GRB 041219A, осуществленной с европейского космического телескопа Integral. Гамма-вспышка GRB 041219A вошла в 1% самых ярких гамма-вспышек за весь период наблюдения, а расстояние до её источника не менее 300 миллионов световых лет. Наблюдение «Интеграла» позволило оценить размер ячейки на несколько порядков точнее, чем все предыдущие опыты такого плана.
Анализ данных показал — если зернистость пространства вообще существует, то она должна быть на уровне 10?48 метров или меньше.»
Так что — зернистости пространства вообще НЕ существует.

Gitkan
23.06.2016 10:05+1Очень элегантная теория!
Возможно, на подобном графе с планковскими рёбрами нейтрино с фотонами это некие глайдеры (планеры) из Жизни Конвея. Ничто не может обогнать глайдер — отсюда и ограничения скорости света =)dimm_ddr
23.06.2016 10:42Что следует из невозможности в Жизни Конвея ячеек напрямую взаимодействовать с несоседними ячейками. Что есть некий аналог принципа локальности нашей вселенной. Что действительно объясняет ограничение скорости света. Так что вы правы в общем-то.
Я могу ошибаться и слишком грубо трактовать какие-то вещи, пусть меня поправят в таком случае более знающие люди.
taujavarob
23.06.2016 18:01dimm_ddr > Что следует из невозможности в Жизни Конвея ячеек напрямую взаимодействовать с несоседними ячейками.
Ограничение скорости света вытекает из принципа неизменяемости законов в инерциальных системах отсчёта.
Так в СТО.

Sliver
23.06.2016 12:19Мне кажется, вот это тут будет очень в тему ;)
https://www.youtube.com/watch?v=4WMrKVST0Hk
Те люди, которые с интересом дочитали эту статью до конца, с удовольствием посмотрят и это видео.
Они сильно перекликаются.
Спойлер: современные физические эксперименты показывают, что пространство и время дискретности не имеют.

napa3um
23.06.2016 12:33Ещё в копилку тематических роликов (они пятиминутные):
https://www.youtube.com/watch?v=Qhowc1PSO4E
https://www.youtube.com/watch?v=JtBHhBpgias

AccessGranted
23.06.2016 12:37Я придумал такую аналогию для теории всего и желания физиков «поженить» стандартную модель с ОТО на примере жидкости.
Каждая молекула жидкости по отдельности не наделяет ее физическими свойствами такими как температура кипения, плотность или теплоемкость для которых существует ряд физических законов. Как только наблюдатель помещается на микроуровень, они видит лишь хоотическое тепловое движение молекул жидкости, но сами законы, которые ранее он наблюдал на макроуровне, исчезают.
Собственно, возможно так происходит и для гравитации, которую мы можем наблюдать на макроуровне, но как только наблюдатель перемещается в микромир она «исчезает».
Соотвественно как для жидкости необходимо определенное количество молекул, прежде чем она начнет проявлять свои физические свойста, так и для гравитации необходимо минимальное количество неких частиц прежде чем сама гравитация начнет себя проявлять.
taujavarob
23.06.2016 18:06AccessGranted > Я придумал такую аналогию для теории всего и желания физиков «поженить» стандартную модель с ОТО на примере жидкости.
Не модно сейчас придумывать модели на основе элементов (жидкости, огня, земли ...) — это было модно в Древней Греции.
Сейчас время математики. — Берите геометрию, или графы или что там ещё знаете — и в путь!

locutus
23.06.2016 13:19Данная идея не может претендовать на фундаментальность, так как в ней время (да и пространство, если присмотреться), вводится как внешний феномен.
В современной теорфизике больше ценятся теории, в которых время и другие свойства возникают из модели, а не вводятся туда вначале.
Банальный пример: волновая функция всей Вселенной в некоторой теории не зависит от времени. Время появляется при попытке отделить один объект от всей остальной Вселенной.
taujavarob
23.06.2016 18:10+1locutus > Данная идея не может претендовать на фундаментальность, так как в ней время (да и пространство, если присмотреться), вводится как внешний феномен.
Если так, вы правы!
> В современной теорфизике больше ценятся теории, в которых время и другие свойства возникают из модели, а не вводятся туда вначале.
Да, особенно в Струнной Теории гордятся тем, что те или иные колебания (!) той или иной струны (или группы струн или формы струн) фактически проявляются в нашем мире как реальные частицы с реальными свойствами.
Древние Греки, любившие не только математику но и музыку, очень оценили бы представление Мира как гармонические колебания неких струн!
Имхо, конечно, имхо.

NLO
23.06.2016 14:16НЛО прилетело и опубликовало эту надпись здесь

OsipovRoman
23.06.2016 14:19Пока что нет.

NLO
23.06.2016 14:41НЛО прилетело и опубликовало эту надпись здесь

OsipovRoman
23.06.2016 15:19Перевод такого труда сложное занятие, он крайне большой и сложный. К тому же Стивен никогда не даст напечатать его на «туалетной» бумаге, как у нас любят печатать книги, поэтому сама книга выйдет еще и около 5000 руб. по стоимости в купе с тем, что эта тема только сейчас становится интересна людям в нашей стране, раньше печатать эту книгу было не целесообразно. Теперь же, в компании уже говорят о том, чтобы сделать перевод и публикацию, так что, думаю, в ближайшие пару лет мы сможем насладиться ею в переводе на русский.

luarviq
27.06.2016 11:46Стивен безбожно путает понятия пространства и материи.
" Допустим, пространство есть сеть. Но что можно сказать обо всех вещах, располагаемых в пространстве? Что можно сказать об электронах, кварках, протонах и прочем?"
Эти «вещи» есть материальные объекты, т.е. сущности, имеющие протяженность. Конечно, можно спорить о том, имеет ли электрон протяженность, но это не меняет сути. Самое интересное, что он сам ответил на свой вопрос уже в заголовке статьи, употребив эйнштейновский термин «пространство-время». Возьмите преобразования Лоренца, и вы легко перейдете из пространства во время и обратно. Пространство — это то, что вы не можете «проткнуть» мгновенно, как лист бумаги иголкой, потому что скорость света конечна. Иногда это кажется парадоксальным. Из этого следует, например, что жители некоей условной галактики, расположенной за 100 световых лет от нас и имеющие мощные телескопы, в следующем году смогут наблюдать штурм Зимнего. Однако то, что скорость света конечна, доказывается в школьном курсе физики (опыт Майкельсона-Морли). И при чем здесь клеточные автоматы, не могу взять в толк, куда их здесь присобачить? Я тоже люблю игру Конвея «Жизнь», это помогает понять, как зарождается порядок из хаоса. Но объяснять на их основе такие фундаментальные понятия — смешно.
taujavarob
27.06.2016 18:20luarviq > Но объяснять на их основе такие фундаментальные понятия — смешно.
Хм, а если взять за основу «струны» — и объяснять на их основе фундаментальные понятия?
Оно смешнее или нет?
luarviq
27.06.2016 18:57Струны — это обобщение четырехмерного пространства-времени на большее количество измерений. Там речь идет о таких объектах, как многообразия Калаби-Яу, от которых крышу сносит почище самогона. Но я, например, легко могу представить математически, как можно наш 4х-мерный мир обобщить на большее количество измерений, Эйнштейн в свое время показал, как это делается, обобщив трехмерное пространство на четырехмерное пространство-время. Вообще, Вольфрам напоминает мне отечественного писателя М. Веллера. Писал себе, писал человек небольшие рассказики, которые кое-кто даже иногда читал. И вдруг, неизвестно с какого перепою, принялся создавать теорию всего. Вычитал где-то про энтропию, что она-де все время увеличивается, а значит, вселенную ждет тепловой кобздец. Его, видите, ли впечатлило название — второе начало термодинамики. Ну и давай применять его к чему не попадя, даже к супружеским отношениям. Бедняга Клаузевиц не мог этого, конечно, предвидеть в 19 веке, когда написал: Die Entropie der Welt strennt einem Maximum zu. Он просто хотел сказать, что разбитая чашка не собирается сама собой в целую, только наоборот. Фактически же он описал стрелу времени, еще до Больцмана. Но Веллеру этого мало. Он ведь хочет, чтобы его книги продавались. Вот и пишет по такому бестселлеру чуть ли не каждый год. Будете в книжном магазине с оказией, нарочно ознакомьтесь, не пожалеете.

taujavarob
27.06.2016 19:16luarviq > Струны — это обобщение четырехмерного пространства-времени на большее количество измерений.
Не всё так сразу:
«В конце 1960-х годов молодой итальянский физик-теоретик Габриэле Венециано искал уравнения, которые смогли бы объяснить сильные ядерные взаимодействия – чрезвычайно мощный «клей», который скрепляет ядра атомов, связывая воедино протоны и нейтроны. Согласно легенде, как-то он случайно наткнулся на пыльную книгу по истории математики, в которой нашел уравнение двухсотлетней давности, впервые записанное швейцарским математиком Леонардом Эйлером. Каково же было удивление Венециано, когда он обнаружил, что уравнение Эйлера, которое долгое время считали ничем иным, как математической диковинкой, описывает это сильное взаимодействие.»
Так что всё началось довольно пресно.
«В конце концов, оно попалось на глаза молодому американскому физику-теоретику Леонарду Сасскинду, который увидел, что в первую очередь формула описывала частицы, которые не имели внутренней структуры и могли вибрировать. Эти частицы вели себя так, что не могли быть просто точечными частицами. Сасскинд понял – формула описывает нить, которая подобна упругой резинке. Она могла не только растягиваться и сжиматься, но и колебаться, извиваться. Описав свое открытие, Сасскинд представил революционную идею струн.
К сожалению, подавляющее большинство его коллег встретили теорию весьма прохладно.»
Прохладно.
«В то время общепринятая наука представляла частицы точками, а не струнами.»
Хм, Почему бы частицам не быть сетью (с поведением клеточного автомата)?

taujavarob
28.06.2016 16:17+1luarviq > Вообще, Вольфрам напоминает мне отечественного писателя М. Веллера. Писал себе, писал человек небольшие рассказики, которые кое-кто даже иногда читал. И вдруг, неизвестно с какого перепою, принялся создавать теорию всего.
Веллер просто прочитал философов типа Гегеля, Канта, да и посовременней (только не постмодернистов — там всё круче) и решил что так рассуждать и писать и он сможет. Ну и начал…
Имхо.

taujavarob
28.06.2016 16:19luarviq > Пространство — это то, что вы не можете «проткнуть» мгновенно, как лист бумаги иголкой, потому что скорость света конечна. Иногда это кажется парадоксальным.
Хорошо. — А что тогда «время»? Мы стоим на месте, допустим, — что нельзя в этом случае «проткнуть» применительно к «времени»?
luarviq
29.06.2016 06:44Время — это переменная, связывающая перемещение и скорость в преобразовании Лоренца
r1 = (r0+v*t)/sqrt(1-v^2/c^2),
где r1 и r0 — радиус-векторы в системах отсчета 1 0.
Если мы стоим на месте (v=0), то при r0=0 формула обращается в нуль. Наша траектория — точка, не имеющая протяженности. Вы скажете — я все равно могу измерить время. Да, конечно. Но как? Вы скажете: пока я здесь стоял, электрон прошел расстояние 1м в вакууме 50000000 раз. Это и будет измеренное вами время, в системе отсчета, связанной с электроном.
Но вот мы начинаем движение. Мы уже не можем игнорировать время, оно незримо присутствует. Каждый бесконечно малый промежуток времени dt генерирует малое перемещение dr (в нашей системе отсчета). Вот почему говорить о времени в отрыве от пространства бессмысленно, отсюда и термин пространство-время, введенный Эйнштейном.
taujavarob
29.06.2016 22:51luarviq > Пространство — это то, что вы не можете «проткнуть» мгновенно, как лист бумаги иголкой, потому что скорость света конечна. Иногда это кажется парадоксальным.
luarviq > Время — это переменная, связывающая перемещение и скорость в преобразовании Лоренца
Про пространство вы хорошо написали, «это то, что вы не можете «проткнуть» мгновенно».
А вот про время — «переменная» — уже совершенно не то. Не впечатляет.
luarviq > Наша траектория — точка, не имеющая протяженности.
Нет, не точка. К примеру, имеем двухмерное пространство-время — стоим на месте. — Мы есть прямая вдоль оси времени.
luarviq > Но вот мы начинаем движение. Мы уже не можем игнорировать время, оно незримо присутствует. Каждый бесконечно малый промежуток времени dt генерирует малое перемещение dr (в нашей системе отсчета). Вот почему говорить о времени в отрыве от пространства бессмысленно, отсюда и термин пространство-время, введенный Эйнштейном.
Мы не начинаем движение. Мы стоим на месте.
Говорить же о времени в отрыве от пространства нельзя по причине того, что каждая точка пространства имеет своё точечное (локальное) время.

luarviq
01.07.2016 17:48Точка не имеет времени. Точка вообще ничего не имеет, даже протяженность у нее нулевая. Это та абстракция, которая сводит с ума обывателя (конечно, если он даст себе труд задуматься над этим) — что-то не имеет длины, но при этом существует. Точка — это чистый объект из мира идей Платона. Как же вы, помилуйте, приписываете ей какое-то там время? Но для точки я могу, вообще говоря, составить какое-никакое хилое определение (Евклид, например, не заморачивался особо и отнес ее в разряд аксиом, чтобы не мучиться с доказательством). В случае же времени это в принципе невозможно. Единственный способ — это определить время через себя, но формальная логика запрещает делать это. Остается определить его через пространство. То, что я написал вам о движении, это, по сути, приравнивание производной ds/dt (чем и является скорость) к нулю. v = ds/dt, dt = ds/v, t = (1/v)Ids, где I — знак интеграла. 1/v при равноускоренном движении — это константа, нам вообще неинтересно, что собой представляет эта обратная скорости величина. Вот вам и время. Можно его мыслить в отрыве от пространства? Никак.

taujavarob
01.07.2016 19:02luarviq > Точка не имеет времени.
Я про график. Про двумерный график одномерно-простанство мира (он же двумерное-пространство-время).
На нём время — всегда прямая у неподвижной точки! — Всегда!

Yuuri
02.07.2016 15:48В обсуждениях не хватает игановской «Лестницы Шильда».
… чтобы поставить серию экспериментов для установления предела применимости законов Сарумпета. Это система фундаментальных уравнений из «Теории квантовых графов», которая позволяет представить физическую реальность в виде полной группы многодольных графов.


napa3um
Вольфрам попался в ту же философскую ловушку, что и Лаплас, только вместо всезнающего математического демона (принципиально не являющегося частью физической вселенной) он придумал выразить все знания этого демона в виде сети. Вроде, не так «религиозно» и антропоморфично, но принципиально ничего не меняет, Вольфрам пытается наделить статусом физического существования математическую структуру, «знающую» о состоянии всей вселенной. Т.е., он, может, и придумает новый мат-аппарат для удобного описания некоторых явлений (например, турбулентности), но эта теория всё равно не станет исчерпывающей теорией всего (просто потому, что это «всё» нам принципиально недоступно, мы взаимодействуем только с локальными моделями явлений в своей голове). «Теория всего» для физики — это что-то похожее скорее на «вероятностный» покер, чем на «строгие» шахматы, с неотъемлемым фактором случайности, риска, статистических обобщений (т.к. любой физический наблюдатель всегда ограничен в пространстве и времени). «Теория всего» для математики — это ИИ, модель познания и представления знаний об окружающем мире в голове математика, и вот тут, возможно, Вольфрам и нащупал некую фундаментальность, найдя базовую математическую абстракцию, с помощью которой можно описать, как наш мозг моделирует явления окружающего мира.
Впрочем, существуют попытки решения этой философской проблемы и постулированием физического существования сразу всех математически непротиворечивых структур (недавно узнал про Макса Тегмарка с его «радикальным платонизмом»), но, мне кажется, это не решение проблемы, а заметание её под ковёр: «все возможные математические структуры» — это просто местоимение для понятия «неизвестность/непредсказуемость». Ещё существует так называемая цифровая физика, которая как раз и пытается отыскать удачные формулировки закономерностей физической реальности в терминах информационных процессов и обмена сигналами, т.е., по сути, в терминах мыслительных процессов наблюдателя, исследующего эту реальность.
(Простите за это псевдоинтеллектуальное графоманство, не смог удержаться.)
OsipovRoman
Безусловно, поднятая проблема крайне сложна. Но вообще Стивен говорит в том числе и том, что вы написали — вычислительная несводимость, которая может поставить крест на таких поисках.
ServPonomarev
Нет, эта структура — и есть Вселенная. она ничего не знает, она просто эволюционирует в соответствии с достаточно простыми правилами, причём, насколько я понял, с высокой долей случайности в своих эволюциях. Просто это находится на таком низком масштабе мироздания, что все эти случайности осредняются и нивелируются, оставляя только «закономерности»
А вот это — весьма ценное замечание:
Даёт надежду на преодоление скорости света и прочие ништяки, необходимые для колонизации хотя-бы нашей Галактики.
napa3um
«Эта структура — и есть вселенная» — нет, эта структура — обобщение математических абстракций на каком-то количестве моделей различных явлений. Различие этих версий — тонкая философская материя (в какой-то степени поддерживаемая научным позитивизмом), а их несводимость друг к другу, возможно, и является фундаментальным законом нашей реальности (или, что в данном случае синонимично, законом существования сознательных наблюдателей), ограничивающим все наши возможные знания о вселенной антропным принципом.
(Простите за это псевдоинтеллектуальное графоманство, не смог удержаться.)
napa3um
В современной науке вопрос о природе пространства и времени (и других явлений) не может быть поставлен без критериев задачи, в которой нужно сформулировать ответ на него. Нельзя просто сказать: «пространство — это граф», это будет метафизическим постулатом, а не физическим. Но можно сказать: «при предсказании эволюции явления, называемого турбулентностью, удобно представлять возмущаемую среду в виде графа с такими-то свойствами». И для другой задачи этот ответ окажется бесполезным, неприменимым.
zuborg
napa3um
Граф — это явление математическое, а не физическое.
OsipovRoman
Ок. А, скажем, круг — это явление физическое или математическое? Мне кажется это довольно «скользкие» высказывания. Особенно учитывая то, что физика имеет своим языком математику.
napa3um
Можно построить множество эквивалентных графу математических структур, какая же из них существует физически? Ответы тут могут быть только философские (например, можно их считать существующими сразу все), выбор ответа ценен только возможностью каких-то дальнейших _полезных_ выводов. А польза вне критериев какой-то конкретной задачи (практической или теоретической) — бессмысленное понятие (потому и вопрос кажется вам «скользким» — вы не можете оценить качество ответа). Эти проблемы решены в рамках позитивизма тем, что их просто исключили из разряда научных. Пока формулы сходятся и предсказания работают (пока есть _польза_) — теория научна, вне зависимости от привлекаемой метафизики. И вот для «теории всего» пока не получается даже качественно сформулировать такую «задачу», в рамках которой её постулаты имели бы физический смысл.
napa3um
Справедливости ради, в более локальном смысле в теоретической физике такая задача для «теории всего» есть, она об обобщении квантовой и релятивистской физики. Но все теории-претенденты (в том числе уже не прошедшие проверку на соответствие экспериментальным данным), в принципе, можно описать в виде графа взаимодействующих друг с другом сущностей. Именно о том я и говорю — Вольфрам нащупал обобщённую структуру всех возможных знаний в голове математика (структуру, различными конфигурациями которой можно выразить все возможные теории), а не «настоящую» структуру нашей реальности (т.е., без описания конкретной конфигурации пространства его граф представляет собой все возможные вселенные, в том числе без наблюдателя, а конкретная конфигурация однозначным образом невыводима только лишь из структуры).
zuborg
Но ведь Стивен под «вселенная — это граф» не имел ввиду абстрактный граф чего нибудь. Да под все что угодно можно подвести понятие «граф», равно как и любую траекторию описать набором эпициклов, но смысл?
В теории Стивена рассматривается граф просто узлов (нуль-мерных, можно сказать), а не каких либо физических сущностей. А вот все-все наблюдаемые физические сущности и явления уже происходят поверх этой сети. В том числе и трехмерность пространства, например.
И ещё вовсе не факт, что таким способом можно будет в принципе описать вселенную. Если можно и мы такое описание найдем — то мы и получим «теорию всего». А возможно, что нельзя — значит идея Стивена оказалась ошибочной.
napa3um
Мы получим «теорию всего» для всех триллиардов математически вероятных вселенных, а не только для нашей. В этом основной смысл моего «уличения» Вольфрама в его «наивном детерминизме». Он нашёл ещё один способ описывать любые вселенные, но без способа выбрать из этих описаний конкретно нашу (точнее, чтобы произвести такой выбор, придётся провести весь корпус экспериментов настоящей физики и получить набор ограничений для «сетки», чтобы она моделировала именно нашу вселенную; причём из одного такого ограничения никак не следуют другие, они невыводимы друг из друга). Примерно с таким же успехом можно бы было сказать, что теория всего — это теория чисел. Тоже универсальный инструмент для описания _чего_угодно_, но вот сами числа исчерпывающих ответов на устройство вселенной не дадут, и физические формулы из них не вывести (но тоже можно перебирать все сочетания символов и проверять их на соответствие реальности). Конечно, какие-то физические ограничения вытекают из математической структуры, но крайне далеко не все.
Я его идею понял как модель «универсальной эволюционирующей системы», на которую можно накладывать разные ограничения из физики и получать различные варианты дальнейшего развития системы, смотреть, какой из вариантов наиболее правдоподобен, и в нём искать новые неизвестные свойства моделируемой системы. Это, по сути, переизобретение так называемой диакоптики (в приложении к анализу физических законов). Это ценный инструмент (метод, подход) для анализа систем, но не «теория всего». Важно понимать, что такая исследуемая математическая структура является слепком не реальности, а лишь наших сведений о ней, и выражает противоречивость или совместимость этих знаний, а не законы физической реальности. Новых законов реальности так не вывести, можно только найти противоречие модели с реальностью. (Я очень похожим способом искал как-то варианты абиогенеза и возникновения генетических механизмов, только у меня была не «модель воздействий», удобная для физики, а «модель преобразований», более удобная для биохимии, хотя они наверняка выразимы друг через друга: http://elementy.ru/novosti_nauki?discuss=432710, комментарий от 15.03.2016 09:01 )
zuborg
Ну извините, но таким образом можно «уличить» и самую настоящую «теорию всего», ведь в реальной Вселенной где-то может летать такой себе Чайник Рассела на орбите, в то время как теория его не предсказывает…
Тут ошибка в слове «любые». Вовсе не любые. Как максимум — счетное множество (ибо кол-во правил эволюции клеточного автомата должно быть конечно, иначе это уже произвол). И вовсе не факт, что его способом можно будет описать нашу Вселенную.napa3um
В общем-то вам извиняться не в чем, вы правильно уловили противоречивость существования «теории всего» вне какой-то конкретной задачи, сформулированной (пусть даже неявно) человеками в силу своих человеческих потребностей (например, вне задачи поиска распределения фарфоровых чайников по галактике). Любая человеческая задача будет локальной в силу локальности самих человеков. (Вообще, об этом можно рассуждать бесконечно, и я, признаюсь, уже исчерпал свой интерес. Вопрос о балансе между теорией и описываемой ею реальностью ещё можно рассмотреть, например, через известную метафору карты и описываемой ею территории: https://ru.wikipedia.org/wiki/Соотношение_карты_и_территории, и опять прийти к антропному принципу, определяющему удобство карт).
synedra
А это почему? Это у вас уже эстетические какие-то категории. В прикладном смысле да, можно обсчитать какое-то конечное количество клеточных автоматов, потому что вычислительные мощности конечны. Но на самом деле их бесконечное количество хотя бы потому, что для любого клеточного автомата, принимающего во внимание N соседних ячеек, существует ненулевое количество автоматов, отличающихся от него только тем, как они обрабатывают N+1-ю (или множество ячеек в N+1-окрестности, это как вам больше нравится). Примерно как числа — для любого N существует N+1.
Этот аргумент, конечно, имеет смысл, когда автомат работает на бесконечном графе/координатной сетке. Ну так клеточные автоматы, способные работать с границами пространства, в котором они живут, или останавливать свой рост — это подмножество клеточных автоматов вообще.
К тому же конечно ли количество топологий графа, на которых будет расти автомат? С уверенностью не скажу, но вроде бы бесконечных периодических графов тоже можно бесконечное количество придумать.
zuborg
То, что кол-во клеточных автоматов бесконечно, это факт, с которым никто и не спорит. Другое дело, что оно счетно…
Речь идет о кол-ве правил, а не автоматов, это две большие, как говорится, разницы ))Есть дискретные системы, эволюцию которых невозможно описать клеточным автоматом с конечным кол-вом правил, но если бесконечно вносить постоянные поправки (правила типа «если достигли такого состояния, то делаем исключение и переходим в такое-то состояние, а не то, что описывалось предыдущими правилами») — то такой «клеточный автомат» можно подогнать под любую систему. Это как раз то, что я назвал «произволом»
napa3um
(Количество состояний всех нейронов в мозге человека конечно и счётно, но это количество на много порядков превосходит количество атомов в обозримой вселенной. Просто на всякий случай добавил в ваш диалог.)
synedra
Тогда я вас неправильно понял, извиняюсь. Да, размер правил каждого автомата должен быть конечным (по крайней мере, я себе автомат с правилами бесконечной длины представить не могу), и множество таких автоматов счётное.
napa3um
(Любой самомодифицируемый автомат можно выразить эквивалентным несамомодифицируемым. Самомодифицируемость правил не делает конечный автомат бесконечным. Если модификации выразимы конечным автоматом, конечно, а не описаны языком, допускающим автореференцию.)
zuborg
Задача всякой «теории всего» — описать исходный (самый низкоуровневый) механизм мироздания, по каким законам (конечно, нет гарантии, что такие законы существуют, но их отсутствие было бы уж совсем удивительным) он работает. Назовем мы результат графом или же другим эквивалентным математическим понятием (например, таблицей взаимосвязей узлов) — значения не имеет вообще, не так ли? Так о чем спор?
Если что-то выглядит, как утка, крякает, как утка,…
napa3um
«Описать исходный механизм» — это опять требует задачу, в рамках которой это описание будет иметь критерии оценки качества, пользы. В физике такая более-менее чёткая задача пока только одна — связь квантовых и релятивистских законов с известными формулами (вывод одного из другого), но вряд ли это поможет предсказать, например, написание данного текста горсткой релятивистских молекул из квантовых полей (хотя на открытие каких-то новых физических явлений, выводимых из такой теории, можно смело рассчитывать).
Отсутствие фундаментального закона, из которого можно вывести все остальные законы естественных наук, не только следствие свойств вселенной («многоэтажности» самоорганизации материи, при которой «этажи» оказываются частично изолированными друг от друга в причинно-следственных связях), но и свойств наблюдателей (их принципиальной локальности в пространстве и времени), рассуждающих об этом. Возможно, я слишком зациклен на антропном принципе и не вижу возможностей его обойти, но не настаиваю на своей дилетантской точке зрения как на единственно верной — уверен, будущее ещё удивит.
sergeypr
Круг — математическое явление, колесо — физическое…
Вопрос (насколько я понял) в том, что есть граф в данной теории? — это какие то поля?, частицы?, энергия?
Представленная теория достаточна «вкусна» с точки зрения получения в дальнейшем «плюшек» (хотя бы возможность получить скорость больше скорости света (при нахождении «прямых» графов между удаленными точками), но не отвечает на основной вопрос — из каких кирпичиков (энергии, полей и т.п.) состоит (и состоит ли?) пространство…
«Граф» же в данной теории просто ярлык непонятному — но никак не ответ на вопрос…
sergeypr
Вдогонку — даже если все так и есть, и мы найдем «нашу» вселенную, по данной теории, то вопрос кто/что определяет поведение этой структуры (например описываемая сеть имеет определенную конфигурацию/связи и ведет себя согласно «программе») остается…
Отсюда следующий вопросы:
— кто/что является агентом связи (может криво написал, но суть такова: что обеспечивает связь/связность узлов сети, ведь в любом известном нам на сегодня взаимодействии есть «агент» — поле или частицы?
— кто/что/какие законы определяют «программу» поведения сети?
napa3um
Если мы найдём «нашу» вселенную, то в рамках научного метода будет неважно, как называть агентов связи — хоть полем, хоть божественной благодатью, сами свойства обнаруженного «агента» и будут определять его смысловое содержание (попробуйте, например, ответить на вопрос, чем является спин электрона).
Вот только найдём мы лишь подмножество непротиворечивых моделей при заданных физических ограничениях на заданном масштабе симуляции физических эффектов в модели. И любое новое явление потребует дополнение модели новыми ограничениями.
sergeypr
-"(попробуйте, например, ответить на вопрос, чем является спин электрона)." — не путайте теплое с мягким!
Спин — всего лишь ярлык, придуманный людьми для описания (классификации) СВОЙСТВА реальной частицы.
То есть это СВОЙСТВО и не важно как мы его НАЗВАЛИ — оно есть и люди привесили ярлык для удобства описания. Нам не нужно знать из чего состоит спин — он просто свойство, не сам предмет.
А в данном случае вопрос не про свойства, а про «состав» — то есть не свойства, а «из чего» — понимаете разницу?
napa3um
Не понимаю. Все слова — местоимения для единиц опыта взаимодействия говорящих приматов с явлением.
sergeypr
Пример: есть электрон — это частица(волна?) — он существует в реальности (?) и у него есть свойства — например спин и масса… мы можем в конце концов его косвенно наблюдать…
Еще проще: есть мячик красного цвета из резины:
-он имеет СВОЙСТВО: цвет — его цвет — красный (красный он потому, что от него отражается преимущественно красный цвет) — то есть все свойства могут быть объяснены при помощи уже известных законов физики.
-он имеет ПОВЕДЕНИЕ: например отскок от земли при его падении — данное поведение обусловлено его материалом (составом) и законами гравитации — опять же имеем объяснения «почему» при помощи уже известных законов…
В данном же случае мы говорим «граф» (сеть) — что это? из чего она состоит? какие механизмы/свойства (чего!?) вызывают/определяют его поведение?
На сегодняшний день, насколько я понял, в данной гипотезе нет ответа на главный вопросы «ЧТО ЕСТЬ ГРАФ?», «Как взаимодействуют между собой вершины графа (посредством чего!?, обмен полями, частицами)?»
Так понятнее?
napa3um
Мне всё ещё непонятно, как в терминах античного атомизма выразить квантмех. И непонятно, зачем это пытаться делать.
sergeypr
Никто и не говорил про «атомизм» — однако, чтобы ПОНИМАТЬ мы должны знать свойства и как управляется/каким взаимодействиям подвержен элемент графа, иначе, это голая абстрактная теория, которую не проверить и не применить…
Пример — атомы состоят из кварков, кварки (очень грубо, но допустим!) из графов…
Строение и механизмы взаимодействия атомов мы немного но знаем… с кварками конечно хуже, но и там есть куда двигаться, по крайней мере направления известны…
В данном же случае — вообще непонятно — ни природа, ни свойства, ни механизм взаимодействия графов.
Самый главный вопрос, конечно же — механизм взаимодействия вершин графа — судя по теории вершины могут быть (в разных измерениях) очень удалены друг от друга, однако теория подразумевает взаимодействия между ними! Вот и хочется понять за счет чего это может происходить?
napa3um
Вы говорите о своём собственном ПОНИМАНИИ, ограниченном атомистическими интерпретациями реальности. С появлением квантмеха наука практически отказалась от критериев ПОНЯТНОСТИ (сводимости к бытовым аналогиям) в своих теориях, оставив это философам. Как сказал Дэвид Мермин: «Заткнись и считай!» (А Ричард Фейман, в свою очередь, сказал: «Квантовую механику не понимает никто».)
taujavarob
sergeypr > В данном же случае — вообще непонятно — ни природа, ни свойства, ни механизм взаимодействия графов.
Аналогия есть.
Если у Эйнштейна ОТО — это геометрия(!), то в данном случае Вселенная — это граф(!).
То есть размышляя о том, как и почему пришли к тому, что ОТО — это геометрия, можно понять и то что предлагается мыслить Вселенную как граф!
sergeypr
Если честно, то пусть хоть магическими линиями объясняют природу пространства — главное для человечества (IMHO) — понять можно ли управлять этим? Если нет, то все эти теории, теориями и останутся…
Размышлять о строении пространства без прикладного смысла — это как разглядывать свой пупок и считать его центром мироздания — смысла столько же!
И я не говорю даже о полном понимании устройства пространства — достаточно просто умения управлять им (пространством)…
Пример положительный: мы не знаем что такое электричество, но умеем им управлять и пользоваться…
Пример отрицательный: мы не знаем что такое гравитация, есть много теорий, но мы не умеем управлять гравитацией
Если исследование свойств пространства приведет к первому примеру — великолепно!, если ко второму — то, практически не имеет смысла…
napa3um
Так в науке и происходит даже без ваших подсказок (с издержками человеческой природы, конечно): экономические задачи двигают исследования в прикладных науках, а футурологические прогнозы на будущие экономические запросы двигают и в фундаментальных. А экономика, в свою очередь, и ставит задачи по управлению ресурсами.
taujavarob
napa3um > Так в науке и происходит даже без ваших подсказок (с издержками человеческой природы, конечно): экономические задачи двигают исследования в прикладных науках, а футурологические прогнозы на будущие экономические запросы двигают и в фундаментальных. А экономика, в свою очередь, и ставит задачи по управлению ресурсами.
Практическая цель постройки БАКа?
napa3um
Я БАК не строил, спросите у тех, кто строил.
taujavarob
napa3um > Я БАК не строил, спросите у тех, кто строил.
Практическая цель постройки БАКа равна нулю!
Имхо, конечно, имхо.
taujavarob
sergeypr > главное для человечества (IMHO) — понять можно ли управлять этим?
Ну, теория ОТО практического значения не имеет же.
sergeypr > Пример положительный: мы не знаем что такое электричество, но умеем им управлять и пользоваться…
Вначале электричество не более чем забавное явления для развлечения полагали.
sergeypr > Размышлять о строении пространства без прикладного смысла — это как разглядывать свой пупок и считать его центром мироздания — смысла столько же!
Иногда это и опасно. Лобачевского за его теорию фактически сгнобили! — Он же занимался тем чего в реальности то и не наблюдалось(!) — Бедняга запирался в актовом зале Универа и замерял углы в надежде найти треугольники где сумма углов не равна 180 градусам!
Да и занятия многими аспектами современной математики есть не более чем «разглядывать свой пупок» — хотя за них и деньги дают и медаль золотую могут вручить. — Но это только за счёт спонсирования государством ли или частными лицами.
zuborg
А выяснить, что из себя представляет такой граф невозможно в принципе. Не могут обитатели компьютерной симуляции достоверно определить на каком железе работает эта симуляция, т.к. у них нет возможности выйти за пределы своей вселенной.
sergeypr
-«Таракан ли Я, „трясущийся от страха“, вцепившийся за кусок материи, несущейся с огромной скоростью в пустоте, или имею право?»
так писал один из авторов фантастики (к сожалению, не помню кто именно)…
Даже, если мы все в матрице — найти ПУТЬ и узнать аппаратную составляющую матрицы, мне кажется, можно — чем собственно и является данная попытка…
drafterleo
Достоевский? — «Мне другое надо было узнать, другое толкало меня под руки: мне надо было узнать тогда, и поскорей узнать, вошь ли я, как все, или человек? Смогу ли я переступить или не смогу! Осмелюсь ли нагнуться и взять или нет? Тварь ли я дрожащая или право имею…» ;)
zuborg
Если бы Вы закончили, скажем, физтех, то были бы в курсе, что математика — это раздел физики )
OsipovRoman
Это тоже крайность, все же. Далеко не все разделы математики «физичны». Или, по крайней мере, нам пока что просто не хватает ума понять их физическую интерпретацию.
zuborg
Это было не строгое утверждение, смайлик намекает )
Основной посыл был, что математики в физике настолько много, что вполне может быть, что она (физика, т.е. реальный мир) состоит из математики на все 99.(9)% (адептов бессмертной души прошу не обижаться и держать под контролем свое самолюбие ;) ).
taujavarob
В известной книге один математик, будучи студентом, попал на лекцию к физикам. Послушав же — пришёл в ужас — математика физиками так вольно интерпретировалась, что он просто сбежал из аудитории. ;-)
vlad72
Наоборот, реальный мир абсолютно нематематичен! Например прямая — где Вы ее видели в природе? Или математическая точка — тоже такого в природе нет.
VoidEx
А окружность в игре «жизнь» есть?
vlad72
Нет, конечно! Но эти математические понятия могут достаточно точно описывать всё происходящее. Вот здесь и задумаешься — что первично?
OsipovRoman
Клеточные автоматы могут генерировать окружности.
Sliver
Клёво!
А можно пример?
OsipovRoman
Да, конечно, скажем, правило 746 для двумерных клеточных автоматов.



В Wolfram Language он реализуется так:
ArrayPlot[CellularAutomaton[{746, {2, {{2, 2, 2}, {2, 1, 2}, {2, 2, 2}}}, {1, 1}}, {{Table[1, {7}]}, 0}, {{{i}}}], ImageSize -> {500, 500}, Frame -> False]
Вот анимация (первые 200 шагов):
Шаг 1000:
Шаг 5000:
Постепенно автомат аппроксимирует круг все точнее.
Есть и другие примеры, конечно.
OsipovRoman
Вообще клеточные автоматы поразительно глубокая вещь. Многие понятия, скажем, та же машина Тьюринга, являются их частным случаем.
vlad72
Математическая окружность, и подобная генерация вообще разные плоскости.
OsipovRoman
Окружность (круг) можно определить через предельный переход от такой конструкции. Так что это вообще не разные плоскости.
vlad72
Функция, приближающаяся к пределу, и сам предел — это разные понятия, существующие независимо друг от друга. Первое в природе существует, второе нет.
OsipovRoman
Хотите жонглировать терминами — ваше право. С таким подходом ничего из математики и физики в природе не существует.
vlad72
Физика существует, математика нет…
OsipovRoman
Если вы хотите пожонглировать, то физика точно также не существует, как и математика. Жаль, что добрая часть комментариев к посту Стивена из того же теста.
Вы путаете понятия «физика» и «существующий мир».
В физике столько же «настоящего», сколько и в математике — сплошь и рядом предельные переходы, бесконечно малые, разрывные функции и прочее и прочее. В этом плане физика просто подмножество математики, которое удачно хорошо позволяет что-то прогнозировать и описывать в «существующем мире». При этом описывает не особо хорошо и детально на данный момент, лишь с определенной погрешностью, вероятностью.
vlad72
«физика точно также не существует, как и математика» — Вы путаете физику с ее математическим аппаратом )) Хотя, безусловно, физика — это тоже описательный процесс. Но я говорил о другом…
napa3um
(Возможно, вам поможет определение такого математического объекта как аттрактор, он конструируется подобным же образом, как круг автоматом). И функции, и их пределы существуют в голове математика равноправно. А в физической реальности существуют системы, приближающиеся к ним.
vlad72
А в физической реальности существуют системы, приближающиеся к ним.…
Наоборот )) математика — абстракция, не соприкасающаяся с реальным миром, но почему-то достаточно точно его описывающая.
Nekto_Habr
Было бы прекрасно почитать статью с подобными примерами и анимациями (тонкий намёк)
:)
0xd34df00d
Я закончил физтех и так не считаю :)
Правда, я примат, мне так положено.
leshabirukov
Вопрос не «верно» — «не верно», вопрос «научно» — «не научно». Нет обоснования — не научно.
pestilent
>а их несводимость друг к другу, возможно, и является фундаментальным законом нашей реальности
Только откуда мы можем вывести этот закон? Есть принцип Бритвы Оккама. Если не будет причин считать, что есть разница между Вселенной и ее математической моделью, то мы должны будем принять, что модель — это и есть сама Вселенная.
napa3um
Бритва Оккама тут совсем неуместна, модель — это математическая, умозрительная сущность, она по определению моделирует реальный прототип явления в интересующих исследователя аспектах, а не является некой платонической сущностью, существующей физически (ну, если вы не «радикальный идеалист»). Такое уж значение у данного слова. А то вы так Оккамой сейчас начнёте резать словарь, пока останется только _ничего_, обозначающее сразу всё (зачем нужны другие слова, если всё — вселенная, а математики — лишь её же часть?).
napa3um
(Т.е., в данном случае речь идёт не о том, как вселенная на самом деле устроена, а о том, как принято это описывать человеческим языком. И вот так грамматика сложилась, что говорить «модель совпадает/не совпадает с реальностью с достаточной для задачи точностью в достаточных для задачи аспектах» правильно, а «модель является/не является реальностью» — неправильно. Ну, если только не в переносном значении в стиле «модель уже является реальностью = данную модель окончательно разработали и описали, она уже используется в практических задачах».)
pestilent
Ну, я имел в виду именно, что модель как абстрактная математическая структура является нашей вселенной. То, что модель не существует физически,— не проблема. Она и не должна существовать. Потому что наша вселенная сама по себе тоже не существует физически. Бритва Оккама направлена против избыточного и необоснованного понятия абсолютного бытия. Вы знакомы с нульмировой интерпретацией квантовой механики? Вселенная существует относительно, например, меня. Или относительно другого наблюдателя, являющегося ее частью. Большего от нее не требуется.
napa3um
В вашей интерпретации уже и вселенная перестала существовать. Не понимаю пользы таких интерпретаций. Понимаю метафоры, поэтические эпитеты и т.п., но вы, кажется, пытаетесь эти метафоры закрепить в качестве аксиом в своей формальной системе, описывающей вселенную, а не передать ими некую эмоцию, для чего обычно подобные метафоры и используют. Люди договорились считать вселенную существующей, так просто удобнее.
pestilent
Поскольку речь идет о нефальсифицируемой метафизике, аксиомы годятся любые :) Но я просто предлагаю как вариант.
Понятие абсолютного существования удобно до тех пор, пока не задаешься вопросом, что, собственно, значит «существовать». Тогда эта концепция начинает только запутывать.
napa3um
Вы аргументируете своей какой-то запутанностью в терминах введение новой метафизики, в которой понятие «не существует» обозначает то, что раньше значило «существует». Что ж, удачи вам в ваших построениях, покажете потом, что получилось (обсуждать недостроенную теорию смысла, очевидно, не имеет).
Существование вселенной — физическое, а не математическое, это важно. Научный метод постулирует существование объективной реальности как данность, а так же наделяет её некоторыми неотъемлемыми свойствами, относительно которых научный метод выводит все остальные.
taujavarob
pestilent >. Если не будет причин считать, что есть разница между Вселенной и ее математической моделью, то мы должны будем принять, что модель — это и есть сама Вселенная.
napa3um > модель — это математическая, умозрительная сущность, она по определению моделирует реальный прототип явления в интересующих исследователя аспектах, а не является некой платонической сущностью, существующей физически (ну, если вы не «радикальный идеалист»).
Хм, является ли летающая авиамодель самолётом?
Если нет — то где грань между моделью и тем что эта модель моделирует?
Очевидно что определение модели не так просто, как кажется. Имхо.
napa3um
Всё верно, понятие модели (и процесса моделирования) — очень комплексное и зависит от контекста. В диалоге речь шла о математических моделях. Авиамодель — это физическая конструкция, моделирующая механику и аэродинамику реального самолёта с пренебрежением его размерами. Математическая модель — это умозрительная конструкция, моделирующая известные и важные математику свойства моделируемого явления. Можно ещё открыть школьный учебник по русскому языку и пробежаться по таким темам как синонимы, омонимы, антонимы, чтобы немного освежить своё понимание лингвистики.
taujavarob
napa3um > Математическая модель — это умозрительная конструкция, моделирующая известные и важные математику свойства моделируемого явления.
А теперь мы эту «умозрительную конструкцию» поместили в компьютер.
С одной стороны этот комп. с этой «умозрительной конструкцией» — с другой стороны вы, за дисплеем (терминалом) этого компа.
И когда мы добьёмся того что не видим разницы между реакцией этой «умозрительной конструкцией» и тем, что она ("«умозрительная конструкция») моделирует — то где грань?
napa3um
Определите _конструктивно_ грань, её необходимость или её невозможность. Я пока не очень понимаю, в каком контексте (в какой задаче) вы пытаетесь отождествить или различить два понятия (провести или разрушить между ними границу). В контексте научного метода принято считать объективную реальность моделью реальности, постулирующей у реальности несколько свойств, в том числе (прямо или косвенно) её существование. Что тут ещё можно пережёвывать? Это просто соглашение, чтобы наделить смыслом все остальные слова в рассуждениях о реальности в рамках научного метода.
Какая разница, что я вам отвечу? Какие дальнейшие выводы вы собираетесь сделать? (Это скорее риторические вопросы, указывающие на бессодержательность нашей беседы, ежели реальная заинтересованность в ответе.)
taujavarob
napa3um > Какая разница, что я вам отвечу? Какие дальнейшие выводы вы собираетесь сделать?
Вы так лихо определили что такое модель — что я подумал что вы сможете мне ответить на мой вопрос.
napa3um
Нет никакого вопроса. «Где грань?» — это не вопрос, это призыв к дискуссии. Грань может быть где угодно, можно долго придумывать примеры с разным расположением такой грани. Предложите хоть какие-то критерии, чтобы можно было хотя бы предположить контекст вашего интереса.
taujavarob
napa3um > Нет никакого вопроса.
Разве? Смотрите:
napa3um > Математическая модель — это умозрительная конструкция, моделирующая известные и важные математику свойства моделируемого явления.
pestilent >. Если не будет причин считать, что есть разница между Вселенной и ее математической моделью, то мы должны будем принять, что модель — это и есть сама Вселенная.
Где грань когда мы сможем считать что модель — это и есть моделируемое явление?
napa3um
Грань для того, чтобы не мочь так считать. А нет грани только в словесных играх в стиле «где грань между фотомоделью и женщиной?»
taujavarob
napa3um > А нет грани…
Если грани нет, то мы находимся вполне себе в модели Вселенной.
Как там это Маск выдал совсем недавно: весь мир есть симуляция.
napa3um
Что бы это ни значило.
pestilent
Я всё-таки попытаюсь еще раз объяснить свою «теорию», зайдя с другой стороны.
Физическое существование чего-либо в нашей Вселенной — исключительно внутреннее дело этой Вселенной. Нет никакого «надмирового» существования, которое позволило бы кому-то или чему-то за пределами нашей Вселенной ткнуть в нее пальцем и сказать: «Эта вселенная существует. В отличие вон от той, например, которая не существует». Именно это я и имел в виду, когда писал, что нет абсолютного бытия, а есть только относительное.
Вселенная существует для нас потому, что мы являемся ее частью. Эта «теория» не такая уж бесполезная. Например, она позволяет не тратить время на размышления о заведомо бессмысленных вопросах, вроде «Почему существует Вселенная?» Первое предложение этого абзаца уже содержит исчерпывающий ответ на этот вопрос.
Конечно, у этой теория могут быть и недостатки, но я и не предлагаю ее как конечный вариант.
napa3um
Это не теория, а принципы позитивизма (если вы делаете акцент на непознаваемости «абсолютных» механизмов вселенной), лежащие в основе современного научного метода. Или антропный принцип, если вы делаете акцент на «самодоказательстве» существования вселенной тем, что мы её наблюдаем. Данные философские позиции, в общем-то, общеприняты, споры идут по большей части о степени «жёсткости» их ограничений.
j-ker
В те же годы, что и автор статьи, я ушёл с головой «во фракталы» — тогда компьютеры стали более-менее мощными, чтобы можно было комфортно этим делом заниматься. Прогуливал занятия в универе, чтобы заниматься там же, но по собственной программе обучения (разумеется, ничем хорошим это не закончилось).
А вот поиски закончились разочарованием (и пьянством, как в комиксе «но я всего лишь хотел...») — куда бы мы (наблюдатели, исследователи) не двигались с имеющимися у нас органами чувств и их расширениями в виде приборов и законов логики (теорией), мы всегда замкнуты в системе, частью которой являемся, частью которой являются органы чувств, методы познания.
И очевидно, что существует «невидимая» часть всего, равно как и «невидимый закон», который с нашей стороны всегда будет выглядеть, как хаос той или иной степени упорядоченности — вот так устроено и всё на этом. Дальше: логический тупик, мистика, НЛО, внезапности…
В общем, тёмная материя-энергия существует, но она вовсе не тёмная, а просто находится за гранью возможного понимания её природы, т.к. любые доступные (в т.ч. в будущем в точке научно-технической сингулярности) знания, методы, инструменты и т.п. являются только лишь частью целого и не могут описать это самое целое, как ни старайся.
KirillGuzenko
Быть может, тёмная материя-энергия всего лишь эпициклы, нужные для корректировки на больших расстояниях.